基于制造成熟度的产品设计方案评价研究*

王晓明 赵 武 陈 领 张 凯 于 淼 于泽源

四川大学 机械工程学院 成都 610065

1 研究背景

制造风险是各企业在研制项目中存在的固有属性,企业由于技术不成熟、生产过程不稳定等不可控因素,可能对产品研发、成本、质量等造成重大影响[1]。为了对产品制造风险进行管控,在产品设计初期全面梳理影响产品研制过程的要素,建立制造能力评估机制。研究制造成熟度等级方案评价方法,对产品设计方案进行有效评价,能够有效缩短产品研发周期,提升资源利用率。

目前,一些学者提出了针对设计方案的评价方法。王海伟等[2]对产品机械设计方案的指标评价矩阵进行规范化处理,引入信息熵对指标权重的不确定性进行描述,并对设计方案进行排序,获得最优的设计方案。王娟丽等[3]应用质量屋计算得到技术参数决策因数,采用0-1整数规划算法获得顾客满意度最大化的技术特性组合,构建变速器产品创新设计方法评价模型。Lin Mingchyuan等[4]通过集成层次分析法和逼近理想解排序法,进行客户需求和产品设计指标识别,完成对产品设计方案的综合评价。高喜超等[5]构建层次分析法-神经网络法组合评价模型,在价值性、可持续性、独特性三个维度上对生产制造与技术开发能力、计划与组织能力等进行了核心竞争力评价。徐晓慧等[6]将机械产品总体设计方案的评价问题描述为不完全多参数决策问题,通过信息熵与有序加权平均算子,建立机械产品方案设计评价的决策方法。然而,以上研究没有结合企业的现实情况,不同企业由于自身特性不同,对设计方案的评价结果是有差异的。寻求一种可以帮助企业有效评估产品设计方案与企业自身的匹配度,管控制造风险的方法,显得很有必要,并具有实际应用价值。

笔者基于制造成熟度,将层次分析法、逼近理想解排序法、模糊集相结合,对产品设计方案进行评价,帮助制造企业分析设计方案与自身制造能力、资金、技术、设备、人员、管理等方面的匹配度,从而选出最佳的设计方案,实现合理利用自身优势,规避自身短板,降低制造风险,获得最大的经济效益和社会效益。

2 制造成熟度评价指标

制造成熟度是评价制造能力是否成熟的一种度量手段,用于帮助项目研制人员评价整个制造体系的成熟度,避免不成熟的制造能力被采用,从而降低所产生的风险[7]。制造成熟度作为一种新的工具,被应用于企业项目实施的各个管理环节中,最大限度满足技术指标要求,降低研制费用,缩短研制周期[8]。

制造要素是制造成熟度的评价指标。笔者从用户、企业、产品三个方面考虑,根据不同的侧重点划分为质量管理、成本、服务、生产设备、制造人员、供应链管理、材料、设计、制造计划九大制造要素。

制造成熟度评估能够帮助项目研制人员在产品设计阶段结束后及时从九大制造要素系统评价产品设计的可能性。考虑到我国民营企业开发新项目时规模小、承担风险低、研发地点单一、不需要外部承包商等特点,笔者提出一套适合我国民营企业特色的制造成熟度评价方法,应用在产品设计阶段结束后,评价产品的制造风险。

3 制造成熟度综合评价方案

笔者将层次分析法、逼近理想解排序法、模糊集相结合,目标是找出与企业最匹配的设计方案。基于制造成熟度的产品设计方案评价是一个多目标属性决策问题,采用逼近理想解排序法能够解决同一企业不同设计方案集的排序问题。在这一优化算法中,需要确定各个制造要素的影响因子权重,采用层次分析法能够有效表达出每个影响因子对于最终制造成熟度判断的权重[9-10]。在逼近理想解排序法的使用过程中,还需要判断不同候选方案的影响因子与最优影响因子、最差影响因子的差异,采用模糊集表示[11],最终将离最优理想解最近,离最差理想解最远的候选方案作为最佳方案。

4 基于层次分析法的制造要素评价算法

制造要素F包含面向用户的制造要素F1、面向企业的制造要素F2、面向产品的制造要素F3。将F1、F2、F3称为一级影响因子,对一级影响因子产生影响的质量管理I1、成本I2、服务I3、生产设备I4、制造人员I5、供应链管理I6、材料I7、设计I8、制造计划I9称为二级影响因子。要得到匹配度值M,需要得到二级影响因子及其权重,根据二级影响因子求得一级影响因子及其权重,最后求得匹配度值M。显然,这是一个多属性决策问题。为了提高计算结果的准确性和可靠性,采用层次分析法计算出各个二级影响因子对于匹配度值M的影响重要程度,定义为权重。

计算各个制造要素的权重,主要操作步骤有四步。

(1) 建立制造要素层次结构。层次分析法的基本特征是具有从属关系的等级层次结构,制造要素层次结构模型如图1所示。

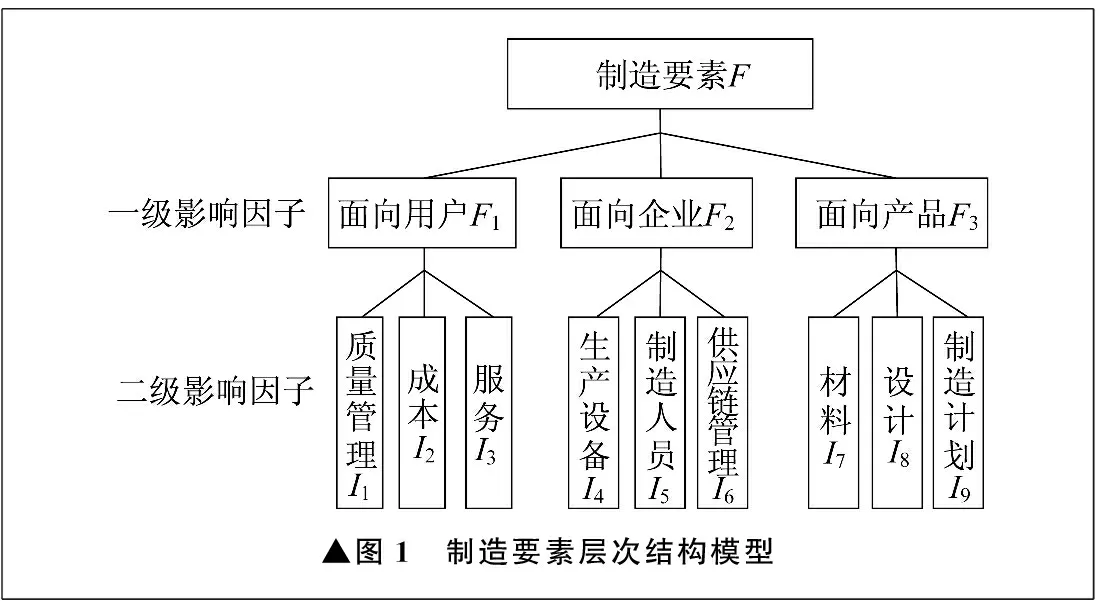
▲图1 制造要素层次结构模型

(2) 构造判断矩阵。基于匹配度值M与一级影响因子的相互关系,构造判断矩阵,如图2所示,反映了制造要素一级影响因子相对于匹配度值M的重要度值。

▲图2 匹配度值M与一级影响因子关系判断矩阵

基于一级影响因子与二级影响因子的相互关系,构造判断矩阵,分别如图3、图4、图5所示。

▲图3 面向用户制造要素与二级影响因子关系判断矩阵

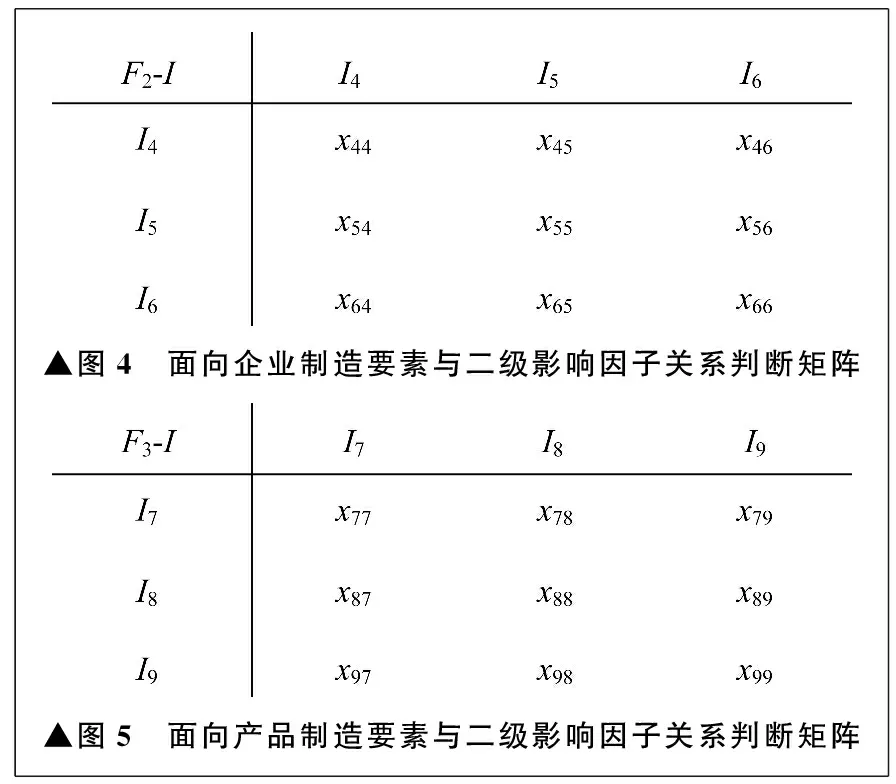
▲图4 面向企业制造要素与二级影响因子关系判断矩阵▲图5 面向产品制造要素与二级影响因子关系判断矩阵

判断矩阵中元素具有以下性质:xij>0;xij=1(i=j);xij=1/xji(i≠j)。

为了使制造要素与影响因子之间的关系量化,需要对xij进行赋值。判断矩阵赋值见表1。

表1 判断矩阵赋值

(3) 一致性检验。计算判断矩阵的特征值,求出最大特征值λmax,由此得到一致性因数CI为:

(1)

式中:n为矩阵的阶数。

对于不同阶数判断矩阵的一致性,需要引入平均随机一致性指标RI,取值见表2。

表2 平均随机一致性指标取值

随机一致性比率CR为:

CR=CI/RI

(2)

当CR小于0.1时,即可认为判断矩阵具有满意的一致性。

(4) 层次排序。层次单排序指根据判断矩阵计算本层次对于上一层影响因子的重要性次序权值,表征本层次对于上一层次需求信息的重要度。

XW=λmaxwm

(3)

式中:X为判断矩阵;W为对应于λmax的归一化特征矢量;wm为W的分量,即对应一级影响因子单排序的权值,m=1,2,3。

笔者计算一级影响因子Fm对于匹配度值M的重要度权重wMFm,并计算二级影响因子Ij对于一级影响因子Fm的重要度权重wFmIj,得到各个层次重要度权重。将各个二级影响因子Ij对于一级影响因子Fm的重要度权重乘以一级影响因子Fm对于匹配度值M的重要度权重,就能得到各个二级影响因子Ij对于匹配度值M的重要度权重ωj:

ωj=wMFmwFmIj

(4)

通过层次排序得到的制造要素影响权重能够客观反映各影响因子与制造要素之间的真实情况,从而为设计人员进行决策提供科学的理论依据。

5 基于模糊集的制造成熟度表示方法

定义模糊集为A,是非空集合U中的一对隶属函数,由tA和fA表示。其中,tA为真隶属函数,fA为假隶属函数。

tA:U→[0,1]

fA:U→[0,1]

设任意z∈U,要求tA(z)+fA(z)≤1,0≤tA(z)≤1,0≤fA(z)≤1。其中,tA(z)为支持z∈A的证据隶属度下界,即为与最优理想解的距离;fA(z)为反对z∈A的证据隶属度下界,即为与最差理想解的距离;1-tA(z)-fA(z)为z对于A的未知程度,称为弃权程度πA(z)。

以闭区间的形式定义模糊集A在任意z处的模糊集值为[tA(z),1-fA(z)],模糊集A能够同时表示与最优理想解、最差理想解的距离。

采用模糊集可以全面表达不同方案对于每一个制造要素影响因子的优劣程度。

在确定制造要素的制造成熟度等级过程中,需要企业结合自身情况组建评审专家团队。为了增强评审的可信度,评审专家团队应该保持一定的独立性。评审专家由项目发起者、企业决策管理者、技术和工艺专家,以及在制造工程、质量管理、供应链管理、设计、生产方面有很深造诣的专家组成。评审专家团队评审设计方案,并到企业现场进行评审,在制造要素的制造成熟度评价指标基础上,判断制造要素的等级。这一过程需要保证不同专家有不同观点,因为不同专家从不同的角度看待评审对象。最终通过评审专家团队会议讨论,由决策者宣布制造要素的制造成熟度等级。

在确定制造要素的制造成熟度等级后,为了便于计算,将等级转换为模糊集值。将制造成熟度等级10级定义为最理想情况,模糊集值为[1,1]。取制造成熟度等级5级为中间值,模糊集值为[0.5,0.5]。制造成熟度等级1～4与6～9均匀对称分布。制造成熟度等级转换为模糊集值见表3。

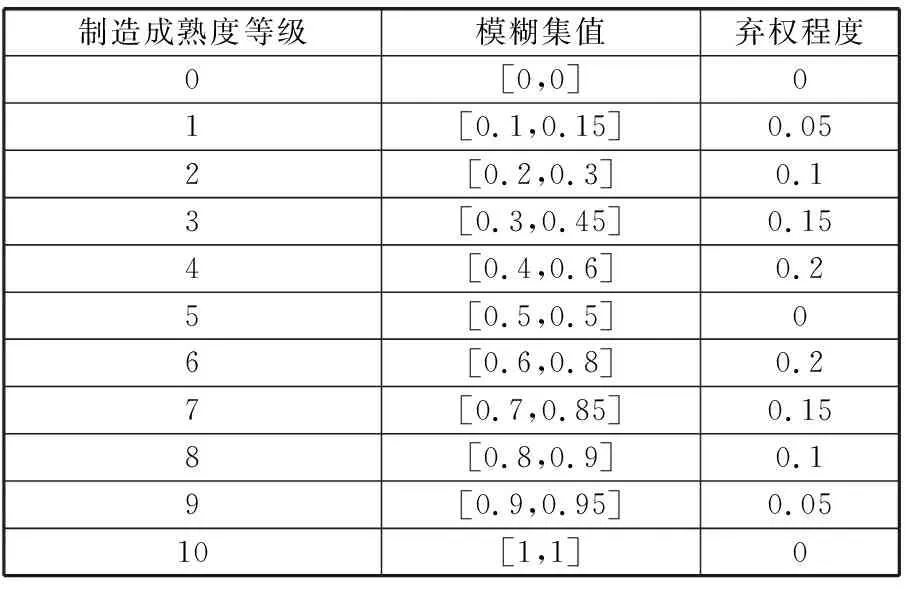
表3 制造成熟度等级模糊集值

6 基于逼近理想解排序法的制造成熟度评价方法

逼近理想解排序法的核心是计算评价对象与最优理想解的距离D+,以及与最差理想解的距离D-,再计算制造要素评价指标,也就是匹配度值M。九大制造要素的制造成熟度是评价对象,最优理想解指制造成熟度处于最高等级,最差理想解指制造成熟度处于最低等级,对多个备选方案进行逼近理想解排序,从而选出制造成熟度等级最高的方案。

(1) 建立最优W理想解和最差理想解。假设第h个备选设计方案为Bh,二级影响因子Ihj的模糊集值为[thj,1-fhj],其中,thj为二级影响因子Inj的模糊集值上界,1-fhj为二级影响因子Inj的模糊集值下界,备选设计方案Bh二级影响因子Ihj的特征由模糊集表示为:

Bh={[th1,1-fh1],[th2,1-fh2],…,[th9,1-fh9]}

构造影响因子最优理想解方案B+为:

B+={[1,1],[1,1],…,[1,1]}

构造影响因子最差理想解方案B-为:

B-={[0,0],[0,0],…,[0,0]}

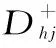
(5)

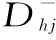
(6)

由此得到距离量度D为:

D([thj,1-fhj],[1,1])=

(7)

D([thj,1-fhj],[0,0])=

(8)

(3) 计算方案Bh的评价指标。根据上述计算结果,可以得到方案Bh的评价指标,定义为方案与企业的匹配度值Mh。

(9)

根据匹配度值的大小排序,匹配度值越大,对应的方案就越好。

7 制造成熟度方案综合评价模型

将层次分析法、逼近理想解排序法、模糊集相结合,在量化评价制造成熟度的同时,也对评价方法的使用模型做出归纳总结。制造成熟度方案评价流程如图6所示。

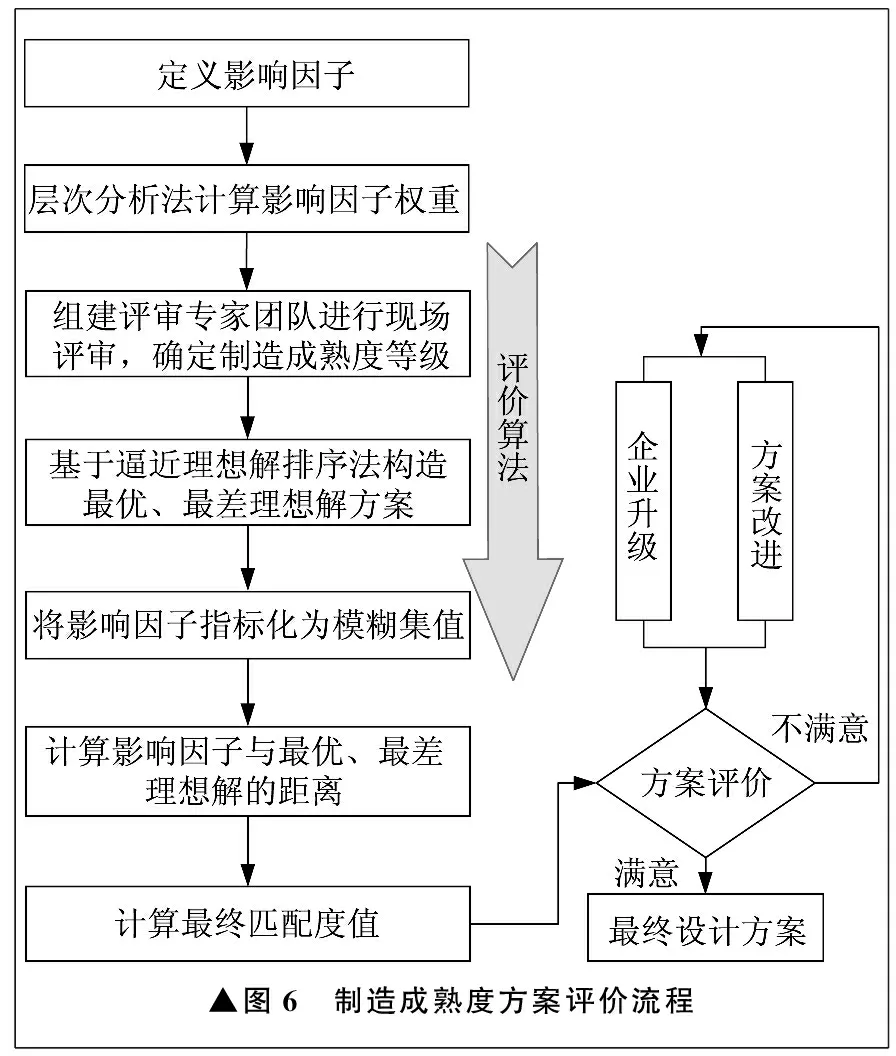
▲图6 制造成熟度方案评价流程

制造成熟度等级评价完成之后,通过计算最终匹配度值,比较各个方案匹配度值的大小,并进行排序。若负责人满意,则选择匹配度值最大的方案作为最优方案。若负责人不满意,则进行改进。制造成熟度方案综合评价模型是一个循环优化的过程,直到最终设计出令企业自身和项目决策者都满意的方案为止。

8 电子水泵制造成熟度方案综合评价

笔者结合电子水泵的制造要素特征进行制造成熟度方案综合评价。

评价对象为某新能源汽车企业生产的电子水泵。结合企业自身现状,经过一系列调研,最终设计出两套新能源汽车电子水泵制造方案。归纳两套制造方案之间的不同点与相同点,见表4。

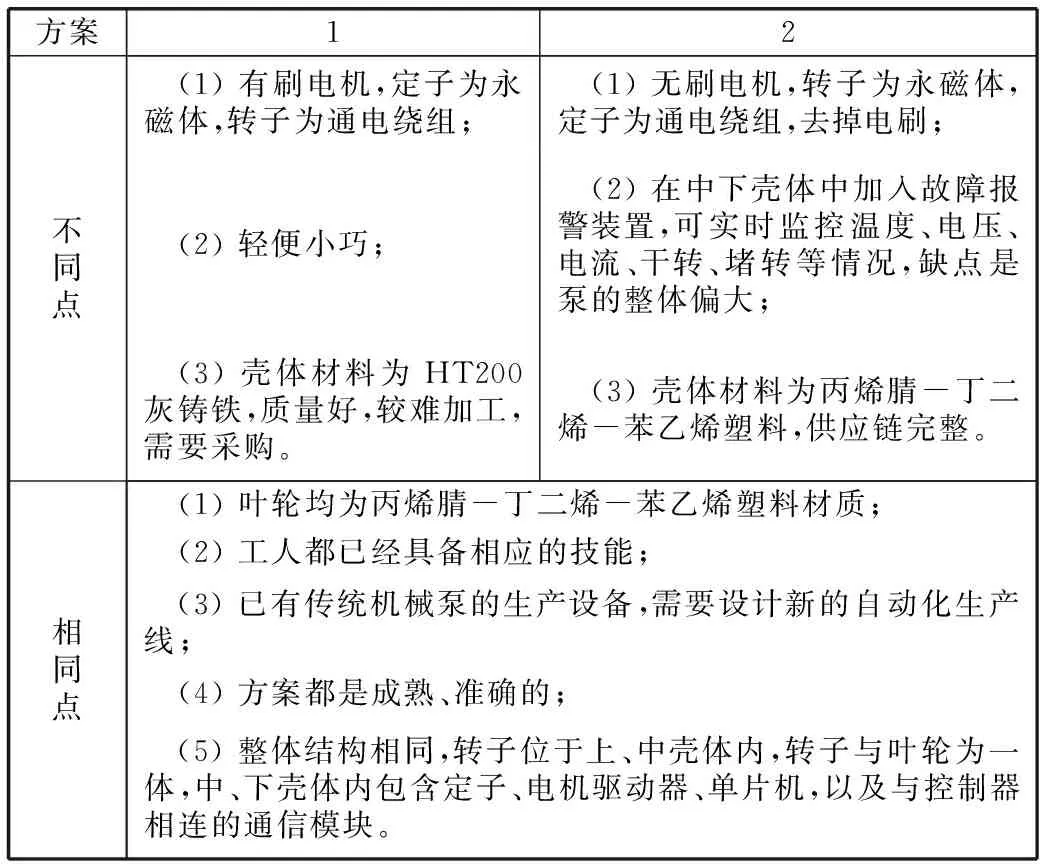
表4 电子水泵制造方案对比

(1) 获取电子水泵制造成熟度的重要度权重。采用层次分析法对电子水泵进行分析处理,确定三个层次制造要素信息之间的关系,对一级影响因子与匹配度值建立一个3阶判断矩阵,对二级影响因子与一级影响因子建立三个3阶判断矩阵。依据对各层次信息之间重要程度的分析,得出相应的数值,建立各层次的判断矩阵。

电子水泵一级影响因子与匹配度值的判断矩阵HM为:

电子水泵二级影响因子与一级影响因子的判断矩阵HF1、HF2、HF3为:

通过对上述判断矩阵的求解,可以得到电子水泵制造要素信息的层次单排序结果:

WM=[0.637 0 0.258 3 0.104 7]T

WF1=[0.666 7 0.111 1 0.222 2]T

WF2=[0.581 0 0.109 0 0.309 0]T

WF3=[0.400 0 0.400 0 0.200 0]T

在获取电子水泵制造要素信息的层次单排序之后,为了验证各判断矩阵中重要程度分析判断的逻辑是否合理,需要对判断矩阵进行一致性检验,结果见表5。

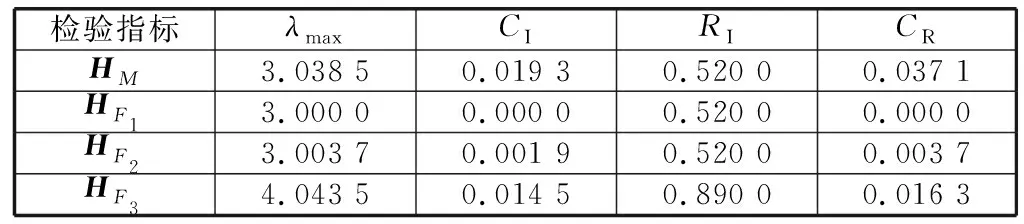
表5 判断矩阵一致性检验结果

各判断矩阵的CR均小于0.1,可以判定判断矩阵具有满意的一致性。将各个二级影响因子对于一级影响因子的重要度权重乘以一级影响因子对于匹配度值的重要度权重,得到各个二级影响因子对于匹配度值的重要度权重,见表6。

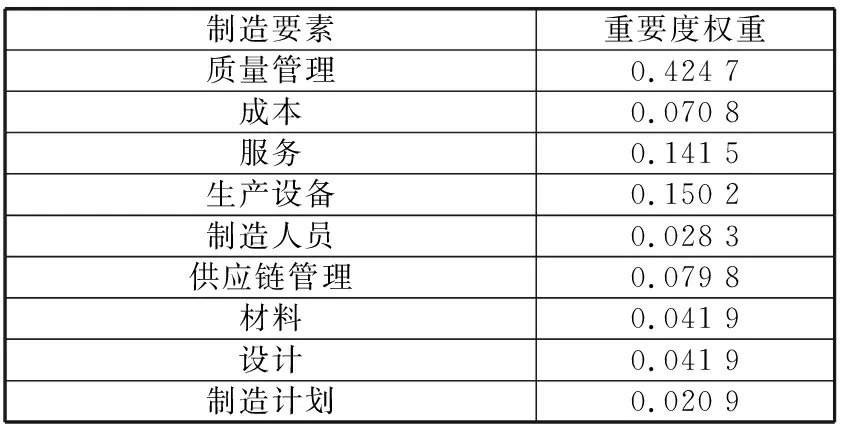
表6 制造要素重要度权重

(2) 获取制造成熟度模糊集。在获取电子水泵制造成熟度重要度权重后,需要在企业中组建评审专家团队,评审专家团队由项目执行者、企业总经理、负责技术的副总经理和产品经理、工艺专家、大学教授组成。专家到企业生产现场评审确定,最后采取平均值确定最终的制造成熟度等级,然后将制造成熟度等级转化为模糊集值。

制造成熟度等级分为0～10级,其中10级定义为最理想情况,对应模糊集值为[1,1]。电子水泵制造方案的制造成熟度等级见表7。

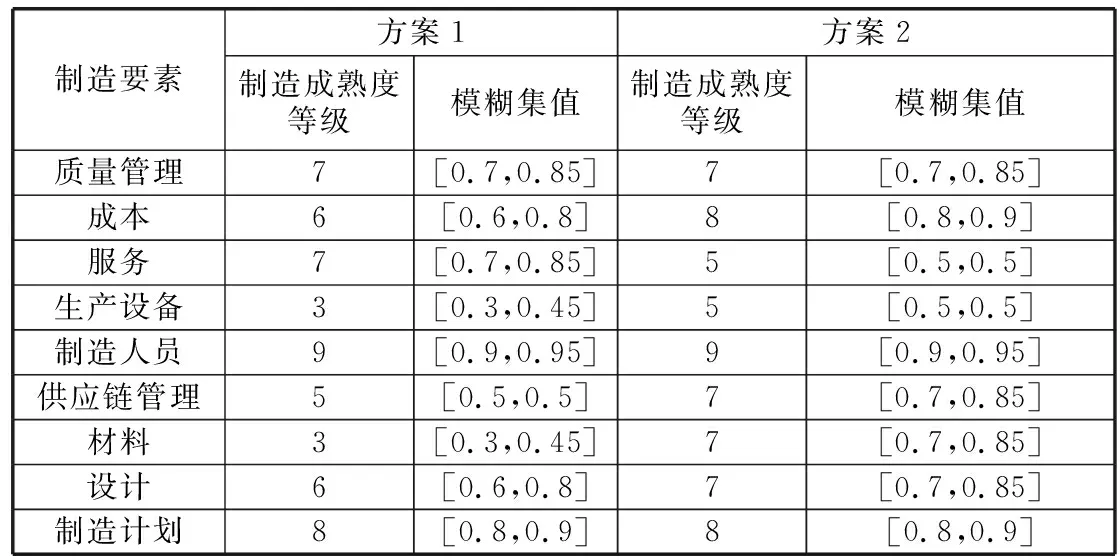
表7 电子水泵制造方案制造成熟度等级

(3) 基于逼近理想解排序法构造最优、最差理想解方案。最优理想解等级为10级,相应的制造要素影响因子模糊集值为[1,1]。最差理想解等级为0级,相应的制造要素影响因子的模糊集值为[0,0]。

最优理想解方案的模糊集B+为:

B+={[1,1],[1,1],…,[1,1]}

最差理想解方案的模糊集B-为:

B-={[0,0],[0,0],…,[0,0]}

计算制造要素影响因子与最优、最差理想解的距离,得到设计方案B1、B2与最优理想解的距离为:

得到设计方案B1、B2与最差理想解的距离为:

最终计算得到设计方案B1、B2与企业的最终匹配度值为:

由此可以得到方案2的制造成熟度目标匹配度值更高,说明方案2更适合企业进行生产制造。最终企业选择方案2作为新能源汽车电子水泵的设计制造方案,新能源汽车电子水泵三维效果如图7所示。

▲图7 新能源汽车电子水泵三维效果

这类电子水泵已实现批量化生产,性能优良,运行可靠,具有较高的经济社会效益,证明了制造成熟度综合评价模型能够帮助企业分析设计方案与自身制造能力、资金、技术、设备等方面的匹配度,选出最佳方案。

9 结束语

为了使产品更好地满足企业制造需求,笔者提出一种基于制造成熟度的产品设计方案评价模型,对多个可行性方案实施评价,帮助企业选择最优方案。以电子水泵为例,通过评价方法选出与企业最匹配的制造方案,经过实际生产验证了评价方法的可靠性。