动态环境下六自由度机械臂在线运动规划算法
2021-02-22庄春刚
柴 铜 庄春刚 张 波
上海交通大学 机械与动力工程学院 上海 200240
1 研究背景
随着工业生产过程中自动化与智能化的普及,人机协作场景的应用变得越来越普遍,人机协作的功能要求也越来越高,如安全性能保障、人机协作装配、智能人机交互[1]等。对于协作机器人,如何保证安全性、生产效率、运动精度[2],是运动规划中的重要问题。安全性要求机器人能够在人体进入工作空间时减速或暂停[3],或者能够对进入工作空间的障碍物,如人的手臂、生产工具等进行避障。生产效率要求在保证安全的同时,尽快完成指定的任务,实现时间最优、能量最优等。
对于运动规划优化问题,首先需要进行几何路径规划,然后针对不同需求进行优化,如时间最优、能量最优、避障规划、消除抖动等。Oberherber等[4]在优化问题中加入扭矩导数项和对扭矩突变的约束,在后续研究中使用分段动态规划得到初始路径,再对初始路径进行B样条曲线逼近优化[5]。比较流行的运动规划方法有协变哈密顿量优化运动规划[6]、随机轨迹优化运动规划[7]、增量轨迹优化运动规划[8]等,一般都使用无约束优化,将碰撞和轨迹抖动作为惩罚项。其中,增量轨迹优化运动规划使用了规划和执行同步进行的策略,提高了实时性,缺点在于每次的规划结果不一定是最优解,因此仍有产生碰撞的可能性。协变哈密顿量优化运动规划、随机轨迹优化运动规划、增量轨迹优化运动规划三种方法的共同点是优化问题的决策变量均为整条轨迹,属于离线规划算法,能够方便找到全局最优解。
Tsai[9]提出一种较为通用的在线实时规划算法,将基于时序的轨迹更新融合至优化问题中,并将复杂的非线性非凸规划近似为二次凸规划,简化了计算。但是这一方法的路径更新是在离散空间中完成的,会引入系统误差。Ragaglia等[10]使用了这一方法,在每个时刻下根据当前环境状态和对一段时间后环境的预测,计算当前时刻的输出量,满足避障要求和动力学约束,并将该输出量传至下层控制器完成控制,实现在线实时规划。文献[10]将所研究的问题定义为线性约束下的二次优化问题,收敛速度快,且不同于增量轨迹优化运动规划,将避障定义为约束,保证了避障的安全性。但是这一方法仍然存在一些缺陷,如未解决任务空间下规划的轨迹抖动问题、任务空间下路径更新的误差问题、局部最优解问题,笔者在研究中针对这些问题提出了解决措施。
笔者借鉴Ragaglia、Tsai等的方法,预先定义一条参考路径,将所研究的问题定义为避障约束下的二次规划问题,可以得到较快的收敛速度,基于此提出一种使用自适应权重参数的关节空间在线规划算法,提高了轨迹的抗干扰能力,避免了轨迹抖动问题,实现了轨迹的平滑。针对真实场景下的规划问题,使用基于卡尔曼滤波的路径更新方法,提高规划过程中路径状态预测的准确性,抑制了系统误差。笔者基于MATLAB软件UR10机械臂平台,进行了算法仿真对比。
2 安全约束建模
为保证人机协作工作空间中人体的安全性,在线规划算法需要实现避障功能。增量轨迹优化运动规划将避障约束转换为目标函数中的惩罚项,进行无约束优化问题求解,但如果发生无解或不收敛的情况,就无法避免碰撞。笔者采用文献[10]的方法,将所研究的问题转换为带避障约束的优化问题,限定优化问题的搜索范围,可以保证安全性。
笔者使用基于Gilbert-Johnson-Keerthi算法[11]的距离估计对约束进行建模。为了简化计算,假设碰撞模型为凸包模型。安全约束建模如图1所示,包括障碍物碰撞模型和末端执行器碰撞模型。
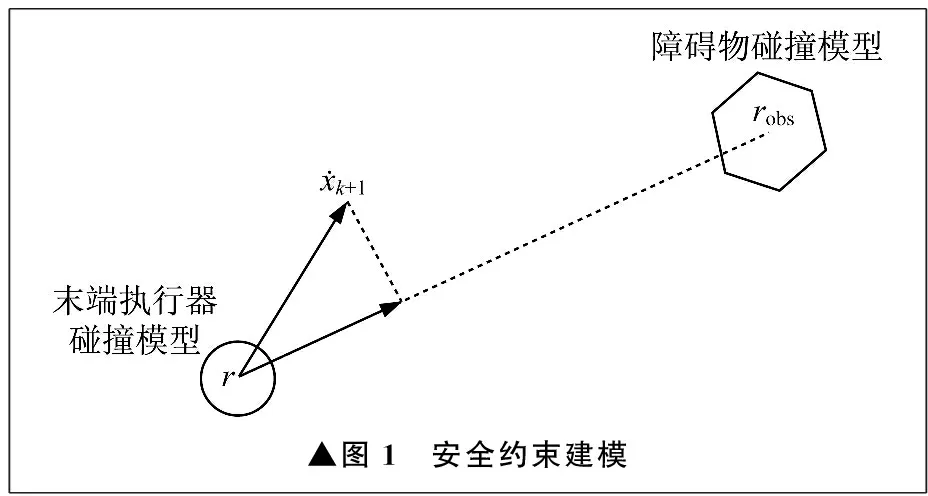
▲图1 安全约束建模
根据图1建立数学模型:
(1)
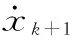
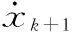
(2)
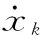
3 优化问题建模
3.1 目标函数
笔者提出的规划算法需要一条参考轨迹作为优化目标,参考轨迹由传统轨迹规划方法得到。参考轨迹在关节空间中可以表示为:
(3)
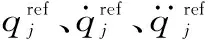
算法的优化目标是使每一时刻的运动轨迹点和参考轨迹点的误差最小,使机器人关节空间的角度、角速度、角加速度对参考轨迹进行跟随,同时对障碍物的距离增加一个惩罚项。将uk作为第k时刻优化问题的决策变量,基于上述参考轨迹定义目标函数为:
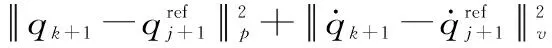
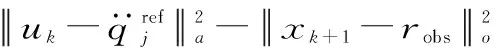
(4)
(5)
(6)
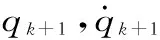
xk+1为:
(7)
式中:xk为末端执行器第k时刻的空间位置。
式(4)中等号右边前三项依次表示对参考轨迹位置、速度、加速度的跟踪,最后一项表示对末端执行器和障碍物之间的距离的惩罚。
综合式(1)~式(7),定义优化问题为:
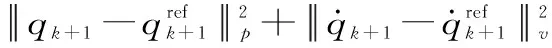
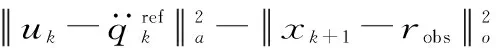
qlow≤qk+1≤qhigh
(8)
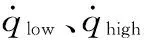
可以看出,该优化问题是有约束二次规划问题,可以直接使用二次规划求解器求解。笔者在仿真中使用MATLAB软件的优化工具箱。
3.2 自适应权重参数方法
对于目标函数中的四个权重p、v、a、o,很多学者通过试验给出了最优值。然而使用已确定的最优值得到的轨迹往往存在振动过大和偏离问题。例如,在没有障碍物的时候,如果参考加速度的跟踪权重过大,那么会使末端执行器的轨迹偏离参考轨迹;在避障过程中,如果仅仅对位置项和速度项进行跟踪,那么会降低轨迹的抗干扰能力,由于传感器引入的误差,轨迹往往会产生较大的振动。对此,笔者提出自适应权重参数方法,使权重与障碍物距离成函数映射关系,用于拟合不同障碍物距离下的权重参数。
考虑到良好的函数性质,笔者使用Sigmoid函数变体来拟合权重参数变化。以加速度误差权重为例,有:
(9)
式中:μ、β、γ、λ为控制曲线形状的参数,μ、β分别控制纵轴方向上的拉伸比例和位置,γ、λ分别控制横轴方向上的拉伸比例和位置。
笔者使用的角度误差权重、角速度误差权重、角加速度误差权重及避障惩罚项权重与距离的拟合曲线如图2所示。
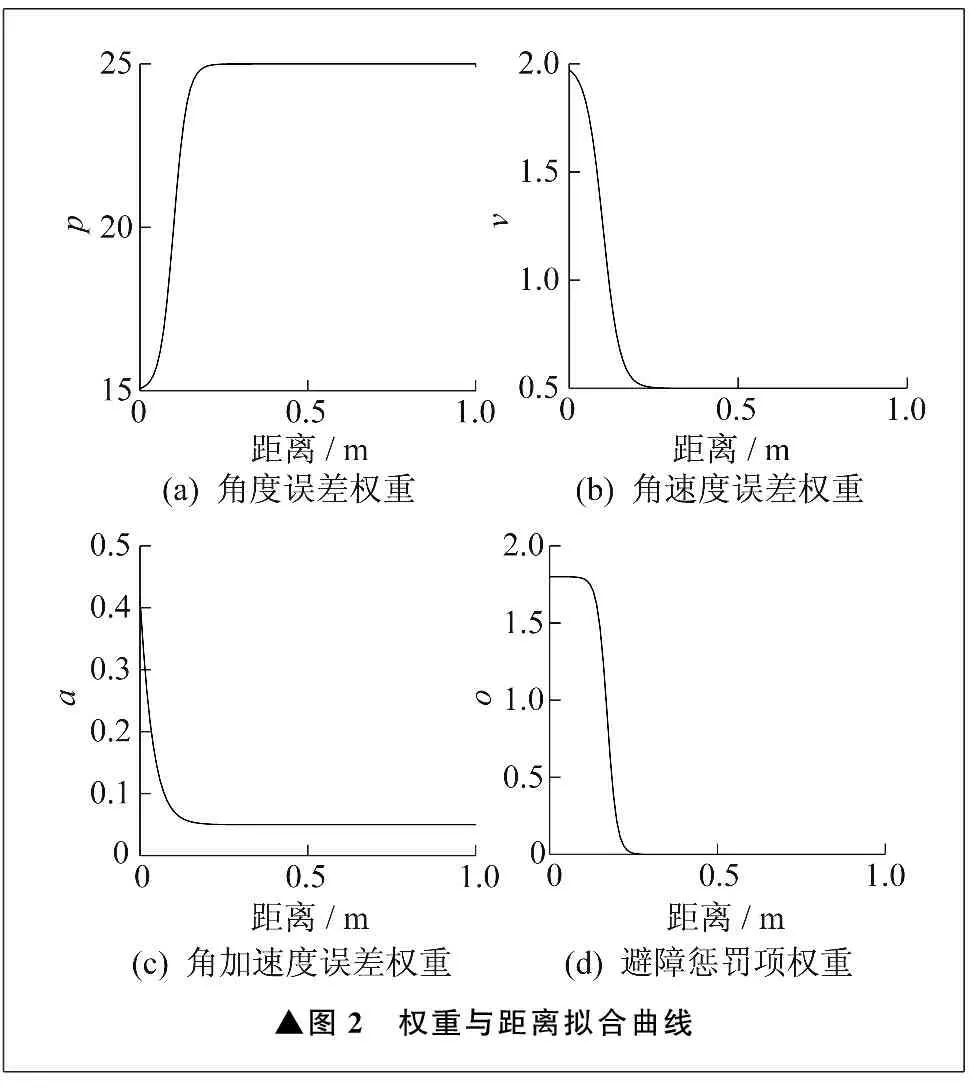
▲图2 权重与距离拟合曲线
4 算法实现
应用笔者提出的在线运动规划算法,在每一个时刻使用二次规划求解器求解优化问题,得到当前时刻的输出,并将控制参数传至底层控制器。在线运动规划算法流程如图3所示。这一算法相比离线规划算法,优势是计算量小,收敛速度快,实时性强。
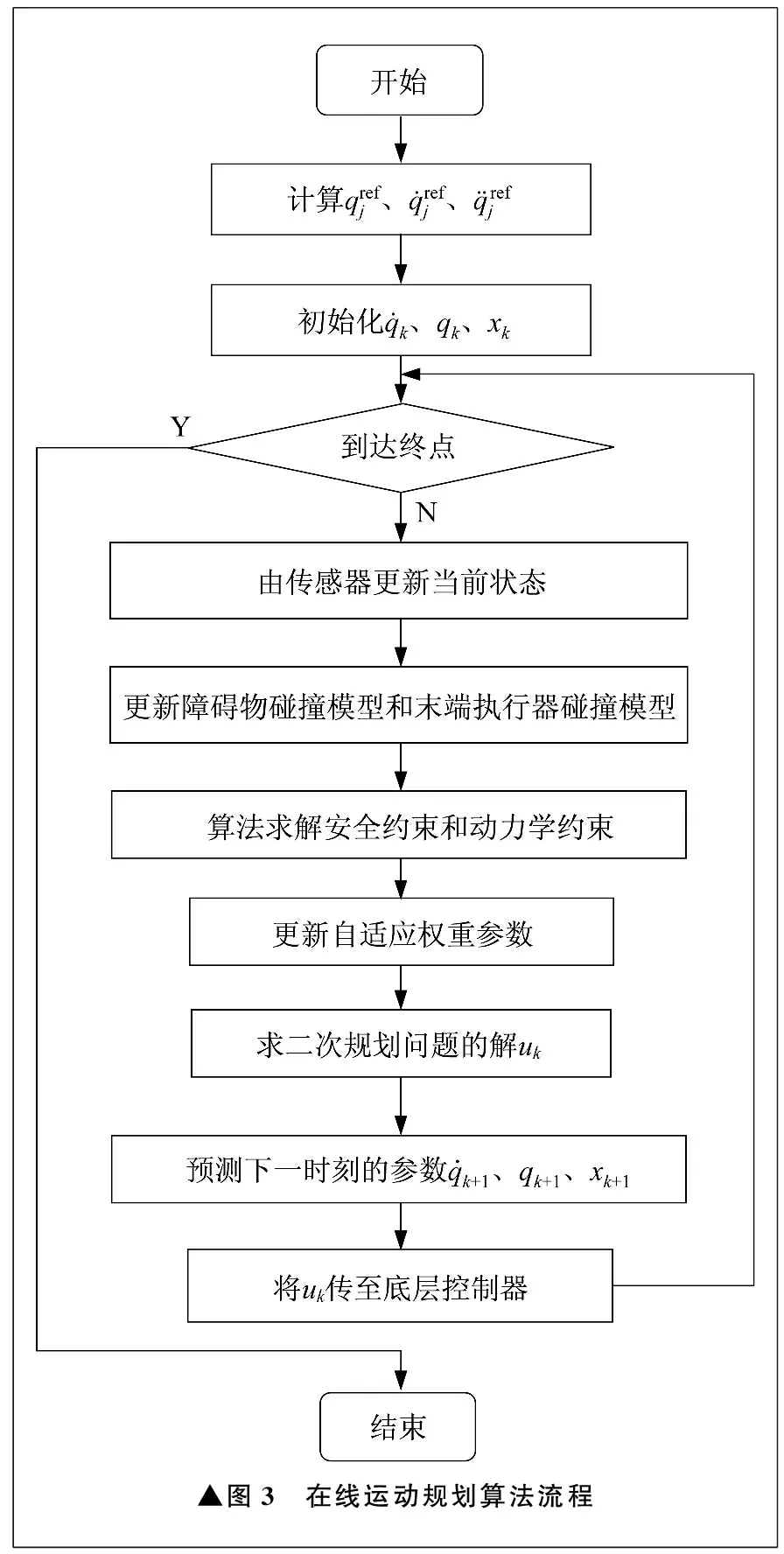
▲图3 在线运动规划算法流程
5 算法仿真
笔者进行了两方面仿真。第一,使用笔者提出的关节空间在线运动规划算法与文献[10]任务空间规划算法进行比较。第二,对自适应权重参数方法和固定参数法的仿真结果进行比较。
计算机仿真环境如图4所示,障碍物碰撞模型和末端执行器碰撞模型均为凸包模型,参考轨迹为预先定义的B样条曲线,实时规划轨迹为使用在线规划算法得到的实际运动轨迹。
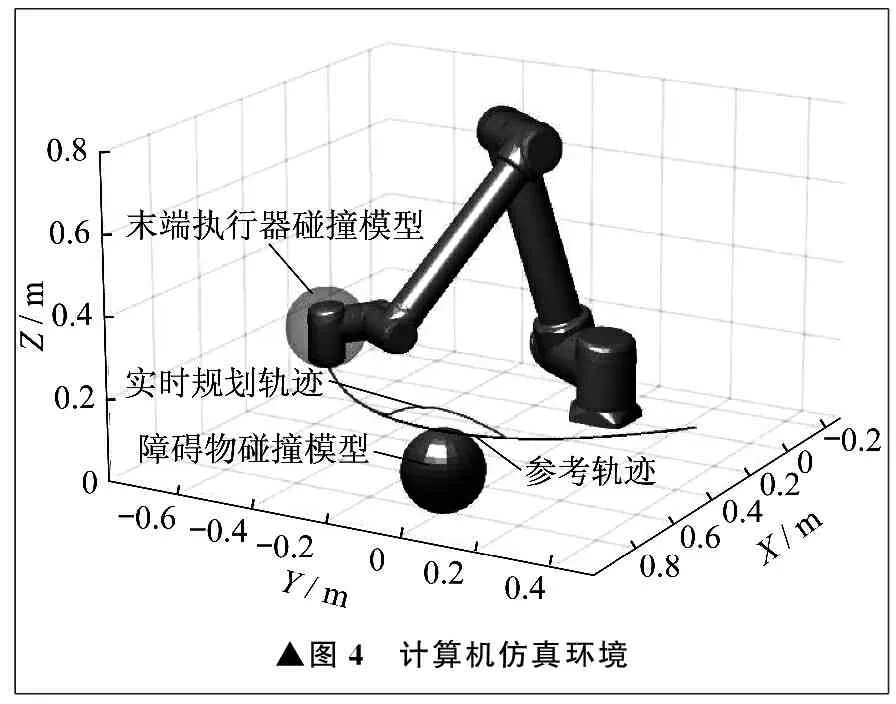
▲图4 计算机仿真环境
为了模拟实际的传感器噪声,笔者在仿真过程中对障碍物模型的位置变量加入高斯噪声,使Gilbert-Johnson-Keerthi算法测量得到的距离符合高斯分布,从而更加接近真实环境。并且,直接对Gilbert-Johnson-Keerthi算法的输出距离加以均值为0、方差为0.003的高斯噪声。
为了评估不同规划算法产生的轨迹的平滑程度差异,除给出直观的轨迹图像外,还使用滑动窗标准差来衡量轨迹的平滑程度。滑动窗标准差原理如图5所示。使用一个固定大小的窗口在轨迹图像上滑动,计算窗口内数据的标准差。这样,对于两条整体轨迹相似但局部振动幅度相差较大的轨迹,可以通过这一方法来量化平滑程度的差异。如果直接计算整条轨迹的标准差,那么无法衡量局部轨迹的平滑程度。同样,窗口宽度太大也无法达到要求,因此必须选择适当的窗口长度和滑动步幅。笔者仿真的滑动标准差窗口长度和滑动步幅分别取1 s、0.5 s。
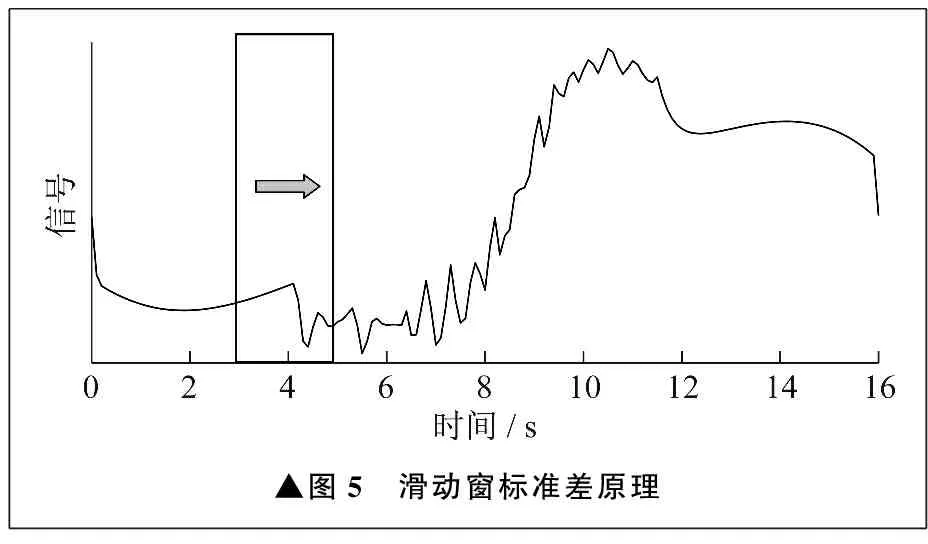
▲图5 滑动窗标准差原理
6 关节空间规划与任务空间规划比较
文献[10]提出的任务空间实时规划算法,在任务空间中对参考轨迹点的位置、速度进行跟踪,轨迹的抗噪声能力较差。
笔者在关节空间中对参考轨迹点的位置、速度、加速度进行跟踪,在一定程度上提升了抗噪声能力,可以有效抑制避障过程中轨迹的抖动。
对比两种不同规划方法在有障碍物的情况下得到的轨迹规划结果,并使用滑动窗标准差来评估两条轨迹的平滑程度。两种规划算法的仿真参数见表1。
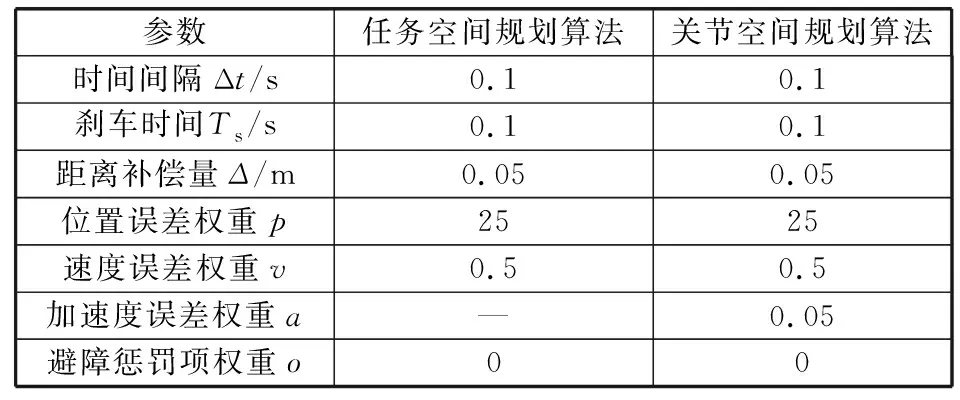
表1 规划算法仿真参数
以UR10机器人关节3为例,关节3轨迹变化曲线如图6所示。两种规划算法均使用了固定参数法。
由图6可以看出,对于笔者提出的规划算法得到的轨迹,关节角度、角速度、角加速度的滑动窗标准差明显减小,相比任务空间规划算法,可以显著减小轨迹的抖动。
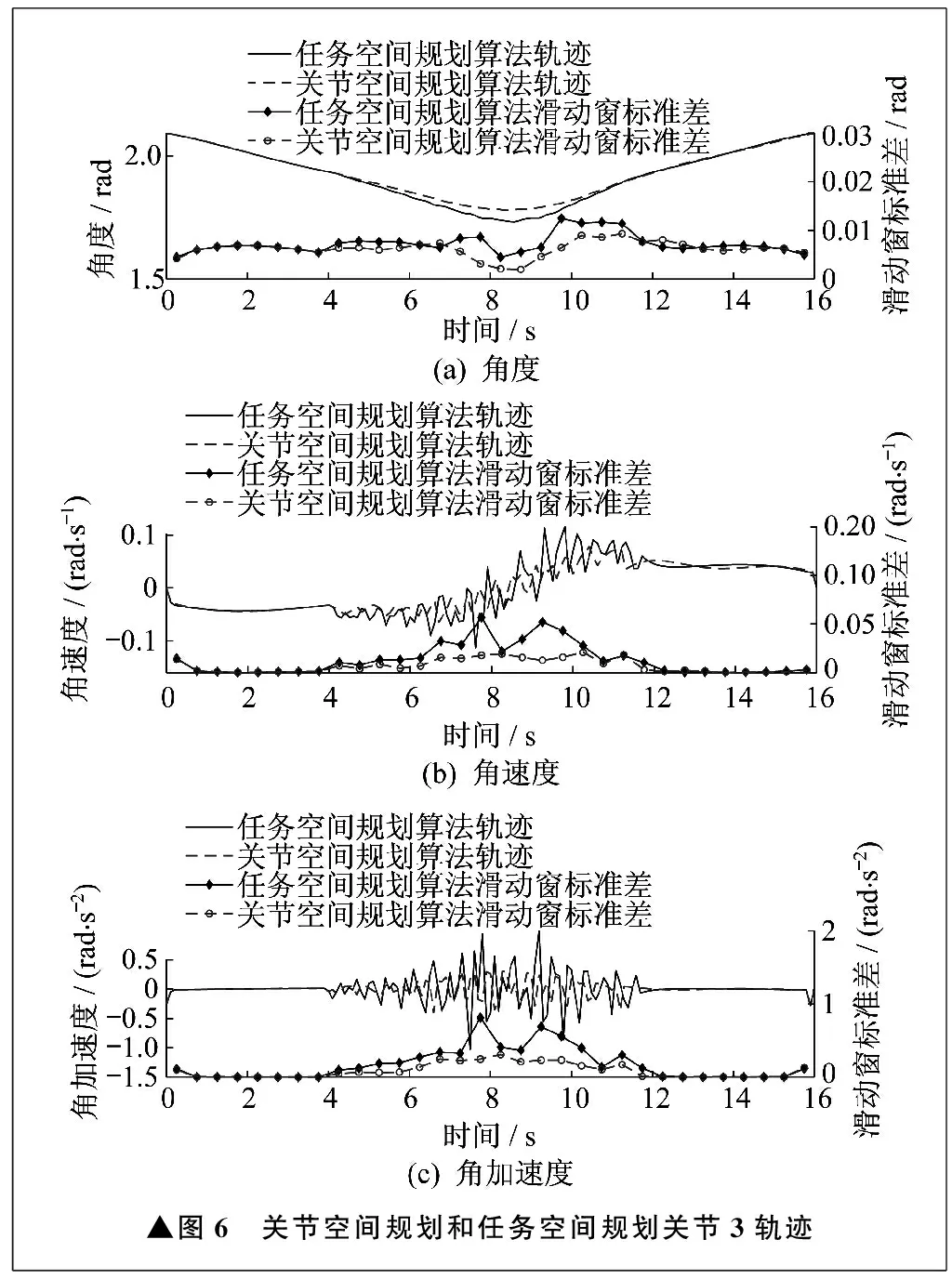
▲图6 关节空间规划和任务空间规划关节3轨迹
7 自适应权重方法和固定参数法比较
笔者在仿真中,关节空间规划算法使用固定参数法,相比文献[10]提出的任务空间规划算法在轨迹稳定性方面已经有很大提升,但避障过程中仍存在轻微抖动。使用自适应权重方法,能够对避障过程中的轨迹抖动问题进行进一步优化,相比固定参数法,轨迹的平滑性可以得到进一步提高。
自适应权重方法所使用的权重拟合曲线参数见表2。
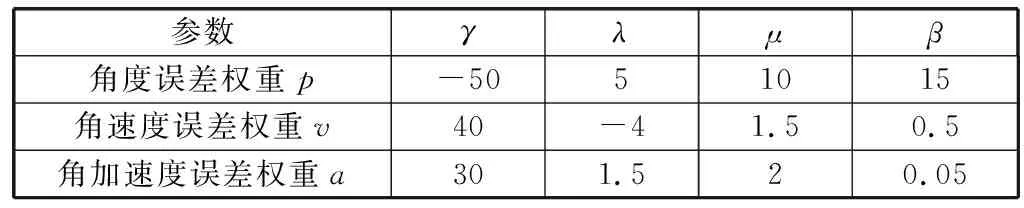
表2 自适应权重方法权重拟合曲线参数
同样以UR10机器人关节3为例,关节3在固定参数法和自适应权重方法下关节角度、角速度、角加速度的轨迹变化曲线如图7所示。
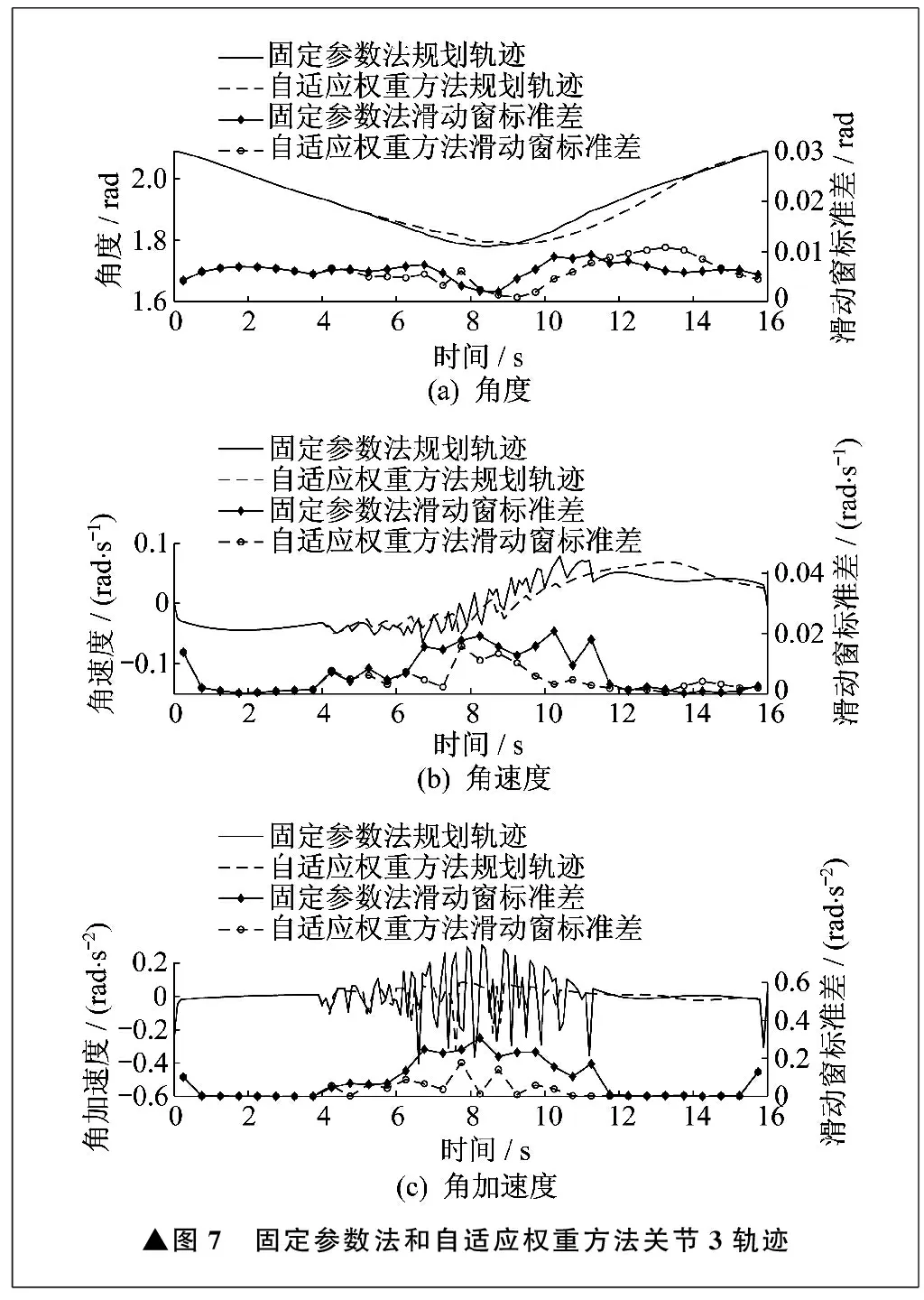
▲图7 固定参数法和自适应权重方法关节3轨迹
由图7可以看出,自适应权重方法相比固定参数法,滑动窗标准差有明显减小,进一步抑制了轨迹的抖动。
滑动窗标准差均值可以在很大程度上反映轨迹的整体稳定情况,均值越小,说明轨迹稳定性越好,均值越大,说明轨迹稳定性越差。综合仿真结果,将文献[10]提出的任务空间规划算法称为算法1,将使用固定参数法的关节空间规划算法称为算法2,将使用自适应权重方法的关节空间规划算法称为算法3,对三种算法的轨迹平滑效果进行比较,计算所有关节的滑动窗标准差均值,结果见表3。
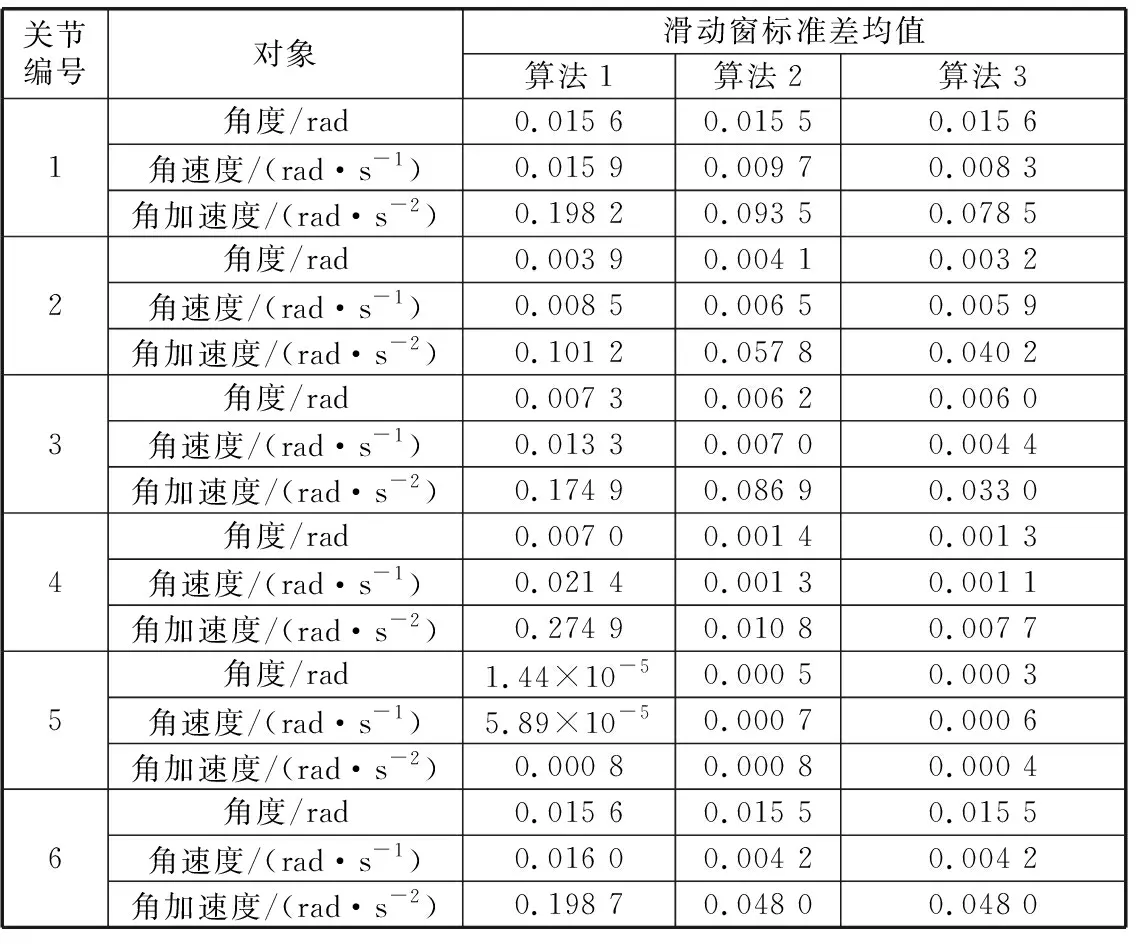
表3 三种算法仿真结果比较
由表3可以看出,对于关节1、关节2、关节3、关节4,角度的滑动窗标准差均值在三个算法中无明显变化,而角速度和角加速度的滑动窗标准差均值从算法1到算法3逐渐减小,说明在轨迹稳定性方面,算法3优于算法2和算法1;对于关节5,由于滑动窗标准差数量级过小,因此即使有明显的提升或降低,也无法对最终轨迹产生影响,效果可以忽略;对于关节6,算法2相比算法1性能有明显提升,而算法3和算法2的效果完全相同。综合而言,算法3优于算法2,算法2优于算法1。
8 结束语
笔者针对人机协作场景的安全性、实时性需求,提出了一种基于自适应权重方法的六自由度机械臂关节空间规划算法,具有实时性强、求解快等优点,能够在避免碰撞的同时兼顾轨迹的稳定性。经过计算机仿真和试验,验证这一算法可行有效。
