菲涅尔定向传光装置仿真及其光学特性分析

2021-02-22陈木生黄金陈泽雄盘雪纯胡艳鑫

中南大学学报（自然科学版） 2021年1期

陈木生，黄金,2，陈泽雄，盘雪纯，胡艳鑫

(1.广东工业大学材料与能源学院，广东广州，510006；2.肇庆学院机械与汽车工程学院，广东肇庆，526061)

在传统的塔式太阳能集热系统中，集热器位于中央接收高塔塔顶，而塔高一般为100～500 m[1]。这增加了集热器前期施工安装以及后期运行维护的技术难度和成本。另一方面，由于传输距离长，传热工质管路热损失大，且需要配备高扬程循环泵，系统能耗增加。基于此，研究人员提出了可避免集热器高空作业的塔底式太阳能集热系统[2−4]。在塔底式系统中，汇聚于塔顶的太阳光线通过塔顶二次反射镜反射至位于地面的集热器，以光线的传递代替传热工质的传输，进而解决集热器高空作业所引发的技术难题。但在塔底式系统中，由于定日镜与二次反射镜距离一般较远，反射光线极易偏离目标表面，因此，对定日镜跟踪精度和安装精度要求很高。此外，由于不同的定日镜与二次反射镜的距离和朝向各不相同，因此，每个定日镜都需要单独的跟踪策略，进一步增加了控制系统的复杂性。为降低塔底式系统中定日镜跟踪策略的复杂性和安装调试的难度，当前的解决思路是：保留塔底式系统地面集中集热的特点，同时将聚光镜场设计成由若干模块所组成，而不同的模块采用相同的跟踪策略和跟踪装置。基于此，周炫[5]提出了菲涅尔二次反射塔式太阳能聚光系统；FEUERMANN 等[6]开发了光纤−微碟式太阳能集热系统；ZHENG 等[7]设计了光漏斗聚光定向传光中央接收太阳能集热系统。前期研究成果表明：以聚光镜场模块化和地面集中集热为特征的新型塔式系统是完全可行的，并且具有巨大的发展潜力。但在新型塔式系统中，所采用的主聚光器基本为反射式聚光器，结构笨重，风载荷大。目前暂未有将菲涅尔透镜应用于塔式系统的文献报道[8]。与反射式聚光器相比，基于菲涅尔透镜的透射式聚光器具有质量小、成本低、聚光效果好、易于加工和批量生产等优点[9]。为此，本文作者针对点聚焦菲涅尔透镜的聚光特点，提出一种可实现聚光镜场模块化和地面集中集热的菲涅尔中央接收式太阳能中高温集热系统，同时利用光学软件TracePro对该系统的聚光模块，即菲涅尔定向传光装置，展开研究分析。研究成果可为开发菲涅尔中央接收式太阳能高温集热系统和菲涅尔定向传光装置提供参考。

1 数值模型

1.1 模型简介

菲涅尔定向传光装置主要由菲涅尔透镜、定向传光器、集热器以及相应的太阳跟踪装置等组成，图1所示为其工作原理示意图。其中，定向传光器为旋转抛物面型反射镜，如图2所示，其固有的光学特性是：位于旋转抛物面焦点处的点源所发出的光线经旋转抛物面反射后会平行于轴线射出。在跟踪太阳的过程中，菲涅尔透镜的聚光焦点相对地面保持不动，且与定向传光器抛物反射面焦点重合。因此，当定向传光器的轴线指向集热器时，菲涅尔透镜汇聚光线在定向传光器反射作用下，将准直射向集热器。

图1 菲涅尔定向传光装置工作原理示意图Fig.1 Operating principle of orientated light transmitting Fresnel concentrator

图2 定向传光器Fig.2 Orientated deflector

在理想状态下，菲涅尔透镜在聚光焦点处形成一个无限小的点，但由于太阳张角的存在，实际得到的是一个具有一定大小的光斑[10]，因此，汇聚光线经定向传光器反射后，形成的反射光线具有一定的发散角度，而非完全平行。当发散角度过大时，部分反射光线将偏离集热器，导致光学效率降低，因此，研究不同的结构参数对菲涅尔定向传光装置光学特性的影响规律具有实际意义和应用价值。

将数量众多的菲涅尔定向传光装置依据一定的设计原则和排布规律组成聚光阵列，同时使所有定向传光器的轴线都指向中央集热器，便组成了菲涅尔中央接收式太阳能中高温集热系统，如图3所示。集热系统中不同布置位置的菲涅尔定向传光装置所采用的太阳跟踪装置及控制策略相同，并且其定向传光器出光口方向在安装完成后便保持不变。菲涅尔中央接收式太阳能中高温集热系统的提出从理论上解决了菲涅尔透镜输出功率与工作效率相矛盾的固有缺陷，为菲涅尔透镜在中高温太阳能集热领域的推广应用提供了新的方法和思路。

1.2 模拟工具及系统设置

随着计算机技术的发展以及计算方法的成熟，考虑时间、人力和物力等实际情况，目前研究人员多采用数值仿真技术对太阳能聚光集热装置展开研究分析[11−12]。本文作者利用光学软件TracePro对菲涅尔定向传光装置进行光学模拟，基于蒙特卡罗法实现光线追迹仿真过程的TracePro已广泛用于太阳能聚光器的辐照度分析，其运算结果可靠[13−14]。菲涅尔定向传光装置三维模型的构建是在三维CAD 系统SolidWorks 中完成的，其中集热器简化为正方形集热板。集热板与定向传光器出光口平行，其几何中心与抛物反射面焦点垂线在旋转抛物面上的交点对齐。

图3 菲涅尔中央接收式太阳能中高温集热系统布置示意图Fig.3 Schematic of medium-high temperature solar collector system composed of Fresnel concentrators and center receiver

模型建立后，导入TracePro中进行光线追迹仿真。在进行仿真试验之前，对光线追迹系统进行如下规定：

1)光源采用格点光源，太阳日盘能量均匀分布，太阳半角为0.27°，入射辐射强度为600 W/m²，总光通量为162.24 W，总光线数为14 872 条，波长的选择及其权重参考文献[15]；

2)菲涅尔透镜材料选择常见的聚甲基丙烯酸甲酯(PMMA)，结构参数如表1所示，不同波长的折射率参考文献[15]，透过率取0.92[16]；

3)定向传光器抛物反射面为理想镜面，反射率为0.9；

4)集热器接收表面吸收率为1；

5)忽略因跟踪误差、安装误差以及光线在传输过程中的能量损耗和光路改变等因素造成的影响。

1.3 定向传光器的数学分析

定向传光器与菲涅尔透镜组合的边缘光线光路如图4所示，其中以抛物面顶点为坐标原点O、定向传光器轴线为x轴，其正方向指向出光口，而y轴正方向则指向正上方的菲涅尔透镜。图4中，O'，p，l0，h0和h分别表示定向传光器抛物反射面焦点、焦准距、截距、出光口高度和汇聚光线分布区域在定向传光器出口方向上的投影高度；f，l和s分别表示菲涅尔透镜焦距、边长和焦斑直径。

表1 菲涅尔透镜结构参数Table 1 Parameters of Fresnel lens

图4 定向传光器和菲涅尔透镜组合的边缘光线光路图Fig.4 Edge-raypath of orientateddeflectorand Fresnellens

为保证菲涅尔透镜汇聚光线均能落入定向传光器抛物反射面，由图4结合边缘光线原理可知，定向传光器结构参数需满足：

边缘光线原理是指从光源发出的光线经光学表面作用后投向目标表面形成光斑，则光源的边缘光线成为光斑的边缘光线。取式(1)中等号成立时的条件，由平面几何关系可知，A点坐标(xA，yA)满足：

又有

在本次仿真试验中，菲涅尔透镜焦平面上能量占比与圆域直径的关系如图5所示。由图5可知：当圆域直径d=50 mm 时，能量占比已经超过99.6%，可视为光斑等效直径。因此，菲涅尔透镜焦斑直径s取50 mm。

将f=620 mm，l=520 mm 和s=50 mm 代入式(2)，联立式(3)解得：

图5 菲涅尔透镜焦平面能量占比曲线图Fig.5 Curve of energy proportion in Fresnel lens focal plane

1.4 试验变量及评价指标

对于菲涅尔定向传光装置，影响其光学特性的主要参数如下。

1)焦准距p，即定向传光器抛物反射面中抛物线焦点到对应准线的距离。依式(4)和式(5)可知，定向传光器截距l0和出光口高度h0由焦准距p唯一确定，因此，定向传光器抛物反射面的结构特征由焦准距p唯一确定。焦准距p越大，定向传光器所需的投资成本越高。

2)几何聚光比C，即菲涅尔透镜采光面积与集热器吸热面积之比，在本次仿真试验中，简化为菲涅尔透镜采光面积与集热板接收面积之比。相应地，系统几何聚光比C0为菲涅尔中央接收式太阳能中高温集热系统中所有菲涅尔透镜聚光面积与中央集热器吸热面积之比。在聚光模块数量相同条件下，C越大，C0越大，中央集热器集热温度越高。

3)传光距离L，即定向传光器抛物反射面焦点到集热器中心的垂直距离。L越大，菲涅尔定向传光装置布置越灵活，同时，菲涅尔中央接收式太阳能中高温集热系统中的聚光镜场规模越大，所收集的能量越多。

菲涅尔定向传光装置光学特性的评价指标包括以下几个。

1)装置内部的光线运动轨迹，尤其是定向传光器反射光线的运动轨迹；

2)光学效率η，即集热器接收表面所吸收的太阳辐射能量Eabs与菲涅尔透镜所接收的太阳辐射能量E0的比值。Eabs和E0通过TracePro计算可得，η由下式确定：

3)集热器接收表面上的能流密度分布，包括最大能流密度Emax、平均能流密度Emean、均匀度FU、焦斑形状及位置变化等，其中均匀度FU可由下式确定[17]：

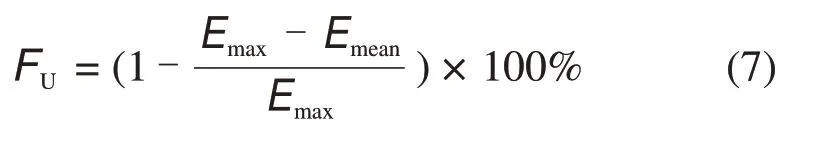
均匀度越大，接收表面能流密度分布越均匀，则越有利于减小或消除接收表面因局部温度过高和温度梯度过大而导致的结构变形和损伤。

2 结果与讨论

2.1 抛物反射面焦准距p

在光线追迹过程中，依据与定向传光器抛物反射面是否有交点，可将菲涅尔透镜汇聚光线分成泄漏光线(无交点)和反射光线(有交点)。而依据光线是否与抛物反射面轴线平行，可将反射光线分成准直传输光线(平行)和发散传输光线(非平行)。一般而言，到达集热器接收表面的光线主要由准直传输光线和部分发散传输光线组成。

不考虑跟踪，且当几何聚光比C=1、传光距离L=1 m时，不同焦准距p的菲涅尔定向传光装置在TracePro 中的光线追迹结果如图6所示。由图6可看出：p越小，反射光线整体越发散。由于反射光线数量众多，且发散角度各异，因此，具体计算每一条反射光线的发散角度是不切实际的。相比之下，装置的整体性能更为关键，故引入“发散系数T”定量描述反射光线整体发散角度。在反射光线传输光路上设置前后放置的两面光线接收板，通过监控反射光线数目的变化以反映发散角度的大小，故可对发散系数T作如下定义：

式中：nah表示穿过前板的光线数；nbe表示穿过后板的光线数。当两面接收板之间距离一定时，发散系数越大，说明从前板到后板之间损失的光线数量越多，即反射光线整体发散角度越大。

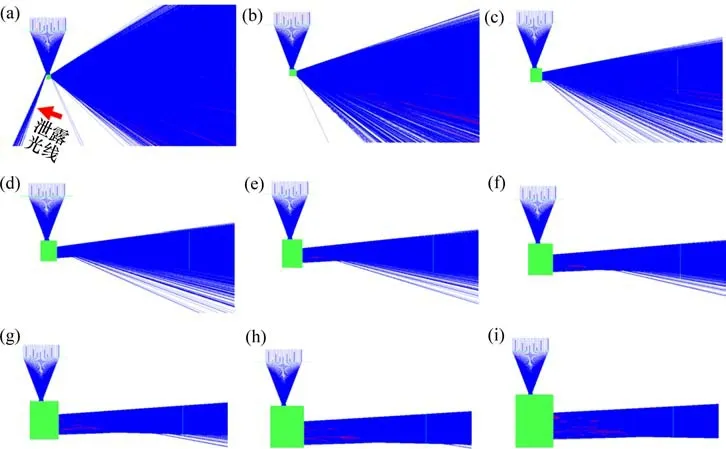
图6 不同焦准距p对应的光线追迹结果Fig.6 Results of ray tracing with different p

试验所采用的光线接收板直径为550 mm，圆心与图4所示的C点对齐，且与定向传光器出光口平行。其中，前板与抛物反射面焦点的垂直距离恒为1 m，后板与前板的垂直距离为Δln。图7所示为发散系数随焦准距p的变化曲线。从图7可见：随着p的增大，发散系数减小且减小速率先增大后减小；而随着Δln的增大，发散系数增大，并且p越小，发散系数增大的幅度越大。结合图6和图7可知：p越大，反射光线整体发散角度越小，即在相同条件下，到达接收表面的光线数量越多。

图7 T随p的变化Fig.7 Changes of T with p

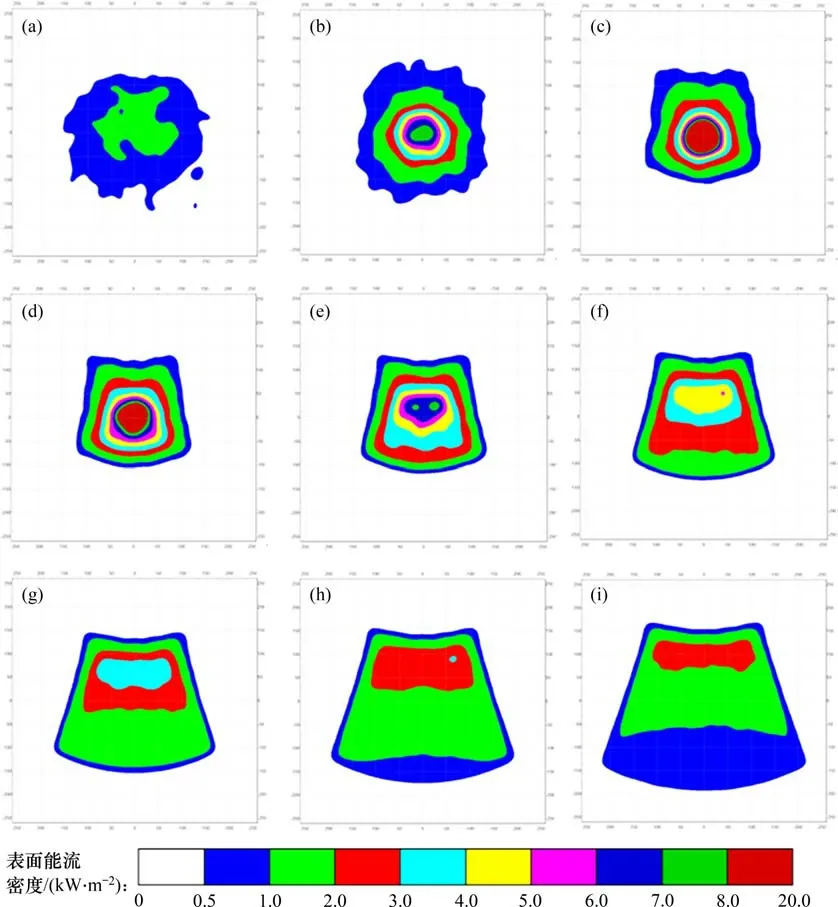
图8 不同焦准距p对应的接收表面能流密度分布图Fig.8 Imaging of flux density distribution in receiving surface with different p

对于不同的p，集热器接收表面能流密度分布如图8所示。图中所显示的焦斑是根据TracePro软件默认的光通量计算门槛值0.05 所得，即光源所发射的光线带有一定的能量，但在追迹过程中会因发生折射、反射和吸收等现象而损失部分能量，当到达目标端面的能量大于初始能量的5%时，端面可显示出焦斑，端面焦斑能流密度采用不同的颜色加以区分。随着p增大，接收表面最大能流密度先增大后减小，在p=100 mm 时取得最大值19 573 W/m2。当p≤100 mm 时，焦斑能流密度分布呈现中心高四周低的特点。这是因为当p较小时，由于发散系数较大，到达接收表面的光线以发散传输光线为主。而交点位于定向传光器抛物反射面上半部的反射光线有向下运动的趋势，而下半部分的有向上运动的趋势，因此，反射光线主要集中在接收表面几何中心处。由于汇聚光线与抛物反射面的交点在接收表面上的水平投影为扇形，因此，随着p的增大，反射光线整体发散角度减小，接收表面的焦斑呈现扇形结构特征，并且p越大，形状特征越显著。而抛物反射面上半部的曲率较大，因此，汇聚光线与抛物反射面的交点更为集中，故最大能流密度位于几何中心偏上方。

装置的光学效率随p的变化曲线如图9所示。由图9可见：当p＜150 mm时，光学效率随p的增大而增大。当p=20 mm 时，对应p＜s时的情形，结合图6和图7，可知此时存在明显的光线泄漏现象，同时发散系数最大，因此，其光学效率远低于其他焦准距的光学效率，故抛物反射面焦准距p必须大于菲涅尔透镜焦斑直径s；当150 mm≤p≤400 mm 时，由于发散系数相对较小，反射光线基本都能准确到达接收表面，因此，光学效率稳定在82.8%左右。但由式(4)可知，随着p增大，定向传光器出光口高度增大，反射光线逐渐向接收表面边缘扩散分布，焦斑面积也随之增大。当p增大到一定程度时，部分反射光线将溢出接收表面，造成光线损失，导致光学效率降低，故抛物反射面p不能无限增大。

如图9所示，接收表面能流密度分布均匀度随p的增大而先减小后增大，在p=100 mm 时取得最小值2.5%。开始时减小的原因：由于定向传光器出光口高度较小，因此，新增的到达接收表面的反射光线主要集中于几何中心，即最大能流密度和平均能流密度两者均增大，但前者增大幅度更大，故均匀度减小。而随着p增大，到达接收表面的光线数量变化不明显，但此时反射光线逐渐向接收表面边缘扩散，即平均能流密度基本不变的同时最大能流密度减小，故均匀度增大。

图9 光学效率和均匀度随焦准距p的变化Fig.9 Changes of optical efficiency and uniformity factor with different p

2.2 几何聚光比C

不考虑跟踪，且当焦准距p=150 mm、传光距离L=1 m时，不同几何聚光比C对应的接收表面能流密度分布如图10所示。由图10可见：随着C的增大，接收表面面积的减小，焦斑分布的相对面积增大。但由于在光线追迹过程中，菲涅尔透镜和定向传光器的结构参数保持不变，即反射光线的运动轨迹保持不变，因此，焦斑能流密度分布特征无明显变化。

图11所示为装置光学效率和接收表面能流密度均匀度随C的变化曲线。由图11可见：随着C增大，光学效率在C＜3时缓慢下降，在C＞3时明显下降。这主要是因为越靠近接收表面几何中心，反射光线分布越密集，则因C的提高而损失的反射光线数就越多，故光学效率下降越明显。由于能流密度分布特征无明显变化而反射光线主要集中在接收表面几何中心附近，因此，随着C增大，接收表面焦斑最大能流密度保持不变的同时能流密度梯度减小，即平均能流密度增大，最终均匀度也随之增大。

在传光距离为1 m的条件下，将光学效率发生明显下降时所对应的几何聚光比定义为极限几何聚光比Clim。Clim越大，则越有利于在保持高光学效率的同时提高集热器接收表面的集热温度，降低集热器投资成本。对于菲涅尔定向传光装置，所设定的C不建议超过Clim。结合2.1 节可知，p越大，所对应的Clim越小。相应地，在菲涅尔中央接收式太阳能中高温集热系统中，菲涅尔定向传光装置的数量k满足：

图10 不同几何聚光比C对应的接收表面能流密度分布图Fig.10 Imaging of flux density distribution in receiving surface with different C

图11 光学效率和均匀度随几何聚光比C的变化Fig.11 Changes of optical efficiency and uniformity factor with different C

2.3 传光距离L

不考虑跟踪，且当焦准距p=150 mm、几何聚光比C=1时，不同传光距离L所对应的接收表面能流密度分布如图12所示。由图12可见：由于反射光线具有一定的发散角度，因此，随着L增加，整体上逐渐向接收表面边缘偏移，故焦斑面积逐渐增大。但随着L继续增大，部分反射光线将偏离接收表面，尤其发散角度较大者，因此，到达接收表面的光线数量减小，故焦斑面积开始减小，同时，最大能流密度和能流密度梯度也随之减小。此外，受反射光线不规则发散的影响，焦斑形状从左右对称扇形结构转变成不规则形状，且L越大，焦斑形状变化越显著。

图12 不同传光距离L对应的接收表面能流密度分布图Fig.12 Imaging of flux density distribution in receiving surface with different L

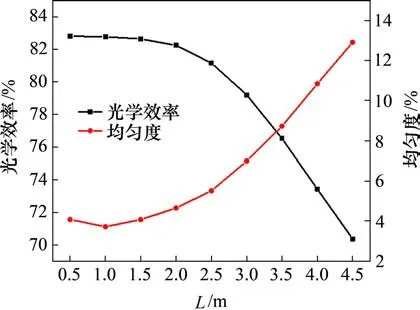
图13 光学效率和均匀度随传光距离L的变化Fig.13 Changes of optical efficiency and uniformity factor with different L

图13所示为装置光学效率和接收表面能流密度均匀度随L的变化曲线。由图13可知：随L增大，光学效率在L＜2.0 m时缓慢下降，在L＞2.0 m时明显下降。结合图12可知，当L=2.0 m时，接收表面焦斑的扇形结构开始被破坏，即大量反射光线开始偏离接收表面，因此，光学效率开始明显下降。当L＜1.0 m时，随着L增大，发散传输光线有向接收表面几何中心会聚的趋势，因此，最大能流密度增大。此时，平均能流密度无明显变化。随着L继续增大，发散传输光线逐渐向四周发散，因此最大能流密度减小。而由于部分反射光线偏离接收表面，平均能流密度减小，但相比最大能流密度的下降幅度可忽略不计。故均匀度先减小后增大，在L=1.0 m时取得最小值3.71%。

在装置几何聚光比为1的条件下，将光学效率发生明显下降时所对应的传光距离定义为临界传光距离Lcrit。当L＜Lcrit时，装置光学效率基本不受L影响。而当L＞Lcrit时，为保持较高的光学效率，可在定向传光器与中央集热器之间连接导光管，以约束反射光线运动轨迹，避免其因发散角度过大而偏离集热器接收表面。结合2.1 节可知，p越大，对应的Lcrit越大。

2.4 跟踪模拟

选取太阳在一年运行过程中的典型位置对菲涅尔定向传光装置进行跟踪模拟。其中太阳典型位置对应春分日(3月20日)、夏至日(6月21日)、秋分日(9月22日)和冬至日(12月21日)等四季典型日期中真太阳时9:00—15:00，时间间隔为1 h的不同时刻。而在不同时刻下的太阳位置可由太阳高度角α和方位角γ共同确定。

太阳高度角α和方位角γ[18]：

太阳赤纬角δ和太阳时角ω[18]:

式中：φ为当地纬度，(°)，北半球为正，南半球为负；n为当日在全年日期中的序号；Ts为真太阳时。地理位置采用广州大学城坐标(113.317°E，23.133°N)；太阳方位角γ以正南方向为起始方向，向西为正，向东为负。

在菲涅尔中央接收式太阳能中高温集热系统中，菲涅尔定向传光装置布置位置不同，其定向传光器轴线的指向也不同。因此，在同一时刻下，不同布置位置的菲涅尔定向传光装置内部光线运动轨迹各异。选取位于中央集热器正南侧和正北侧的2个典型布置位置的菲涅尔定向传光装置进行分析。当p=150 mm，C=1 且L=1 m 时，光学效率变化曲线如图14所示。由图14可见：对于同一日期的不同时刻，随着时间的推移，正南侧的菲涅尔定向传光装置的光学效率先下降后上升，并且关于真太阳时12:00对称，但夏至日的光学效率基本不随时间变化；而正北侧的菲涅尔定向传光装置的光学效率则无明显变化。对于不同日期，正南侧的日平均光学效率差异较大，其中夏至日最高，为82.76%；冬至日最低，为17.83%，仅为夏至日的21.54%。而正北侧的日平均光学效率基本稳定在80%～83%，其中春分日和秋分日最高，为82.65%；冬至日最低，为81.48%。

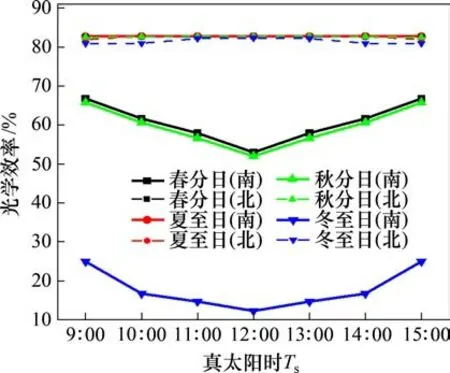
图14 光学效率随真太阳时Ts的变化Fig.14 Changes of optical efficiency with Ts

图15 春分日不同Ts对应的光线追迹结果Fig.15 Results of ray tracing with different Ts on Spring Equinox

图16 泄漏光线数量随真太阳时Ts的变化Fig.16 Change of number of loss rays with Ts

图15和图16所示分别为春分日不同真太阳时所对应的光线追迹结果和泄漏光线数量变化。由图15可知：在跟踪太阳过程中，定向传光器出光口一侧有泄漏光线的产生，对于中央集热器正南侧的菲涅尔定向传光装置尤为明显。而对比图16和图14可发现：光学效率的变化与泄漏光线数量的变化存在直接联系，泄漏光线数量越多则光学效率越低，泄漏光线数量增大则光学效率降低。这表明在跟踪太阳的过程中，泄漏光线数量的变化是导致光学效率变化的直接原因。当菲涅尔透镜偏向定向传光器出光口一侧时，无明显光线泄漏现象发生，因此，光学效率相对较高。当菲涅尔透镜偏向定向传光器顶点一侧时，有大量泄漏光线的产生，因此，光学效率普遍较低。对于正北侧的菲涅尔定向传光装置，虽然在夏至日时，菲涅尔透镜偏向定向传光器顶点一侧，但由于此时太阳高度角和方位角绝对值相对较大，在1 d跟踪太阳的过程中，所产生的泄漏光线数量有限，因此，其光学效率相对较高。

结合上述分析，基于提高菲涅尔中央接收式太阳能中高温集热系统光学效率的考虑，应将菲涅尔定向传光装置重点布置在中央集热器北侧，但此时集热系统存在遮挡问题，主要包括中央集热器对菲涅尔透镜的遮挡，以及菲涅尔透镜自身对反射光线的遮挡等，因此，后续研究应着重解决镜场分布的优化设计，并且该集热系统不建议在全年太阳高度角较小的高纬度地区使用。此外，在安装空间和投资成本等条件允许的情况下，适当增加定向传光器的截距有利于提高集热系统的运行性能和经济性。

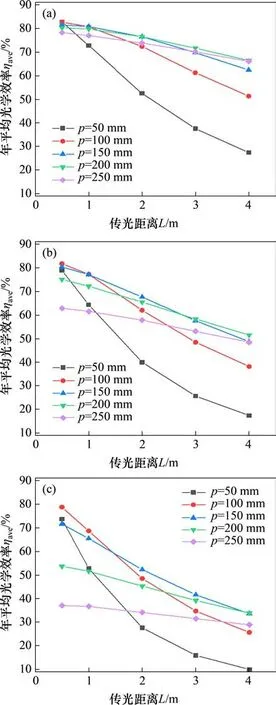
图17 年平均光学效率随传光距离L的变化Fig.17 Change of yearly average optical efficiency with different L

取4个典型日期的日平均光学效率的平均值作为年平均光学效率的参考值，则位于正北侧的菲涅尔定向传光装置在跟踪过程中，年平均光学效率随传光距离L的变化曲线如图17所示。由图17可见：随着L的增大，年平均光学效率降低，但p越大，下降幅度越小。而随着C的增大，年平均光学效率降低，且p越大，下降幅度越大。这表明随着p的增大，反射光线对接收表面面积的变化更敏感，即在跟踪过程中焦斑更容易偏离集热器；但反射光线整体发散角度减小，更有利于长距离传光。在C和L相同时，定向传光器抛物反射面存在最优焦准距popt。当ppopt时，准确到达集热器的反射光线数量增多，但在跟踪过程中偏离集热器的反射光线数量也增多，日平均光学效率降低。当C≤4 且L≤4 m 时，最优焦准距popt位于150～250 mm之间。