基于相变线源解的固液热导率测量方法及其影响因素分析

2021-02-22周天袁杰马爱纯

中南大学学报（自然科学版） 2021年1期

周天，袁杰，马爱纯

(中南大学能源科学与工程学院，湖南长沙，410083)

为了克服快速城市化和化石燃料资源枯竭导致的能量供需缺口不断扩大的情况，开发提高能源利用效率的新技术已成为国内外学者关注的研究热点。相变材料(PCMs)作为有效利用能源最合适的材料之一，在相变过程中具有可控性强、储热密度高的特点，被广泛应用于太阳能储存[1]、热管理[2]、建筑节能[3−4]和废热回收[5−6]等领域。相变材料的熔点、相变潜热及热导率是各种相变储热应用的主要选择标准，其中相变材料在相变点附近的热导率是支配具体相变储热过程的真实热物性参数，对相变储热应用的效率、性能有着重要影响，是相变储热应用设计和性能评价所必需的重要热物理性质之一。特别是在实际应用中，相变材料的应用价值在于相变点处潜热的释放/吸收过程，因此，精确掌握相变材料在相变过程中相变点附近的热导率对于相变储热技术的工程应用和科学研究至关重要。传统的热导率测量方法中，瞬态热线法(THW)[7−8]和瞬态平面源法(TPS)[9−10]由于测量速度快、量程大和温区适应性广等优点被广泛用于相变材料热导率测量。尽管THW 法和TPS法已成熟，但在测量过程中只能测试物质在某一物态下的热导率，且未考虑相变过程中潜热的释放/吸收对测试过程的影响，当测试物质接近熔化温度时，基于理想化理论测量热导率的THW法和TPS 法测量结果会呈现出“动态变化”的异常现象[10−13]。认识到传统测量方法的局限性，学者们通过对不同边界条件下相变模型的相变过程分析提出了一些可行的热导率测量方法。基于Stefan第一类边界条件约束下的内熔问题，ZHOU等[14]用拉普拉斯变换法分析了热导率与相界面移动速率的关系式，并且通过记录相界面位置的时间曲线得到了较为精确的2个无机相变材料的热导率。基于第二类边界条件，ZHANG 等[15]建立了改进的瞬态热线方法(ITHM)，通过在THW的测量模型中添加一个表示潜热释放/吸收的源项，从数值上纠正了电热引起的测量误差；YANG等[16]采用准静态近似方法提出了一种基于一维相变过程的“T-melting CHF”方法，通过记录恒定功率加热下的温度−时间曲线得出PCM 的导热率、熔点和相变潜热。基于第三类边界条件下的相变模型分析，ZHANG等[17]提出了参比温度曲线法(T-history)，通过记录被测物质和参比物质的温度−时间曲线计算得到被测物质的热物理参数。除此之外，PALOMO DEL BARRIO等[18]设计了一种简单的定形相变材料热物性参数测量方法，通过求解正则化算子得到相变函数以反演得到热导率。上述研究给人们带来新的认识同时，自身还具有一定局限性。例如，在计算过程中，ITHM 需要多次迭代才能获取最终值，并且步骤繁琐[15]；而T-melting CHF 方法采用准稳态熔融模型，忽略了控制方程的瞬态性质，只适用于小Stefan数的情况[16]；基于集中参数假设的T-history 方法对样本的长径比有严格的要求[17]；正则化方法受到材料固相和液相热导率一致性要求的限制[18]。除此之外，上述几种方法一次测量都只能获得单相热导率。本文作者提出一种同时获得相变材料固液两相热导率的测量方法，扩展热物性测量方法的范围，将测量范围扩展到包含相变的材料和多个导热系数的估算。该方法使用无限相变线源解来解决圆柱坐标中的Stefan问题，通过测量空间某一监测点液相温度曲线来拟合得到材料固液两相热导率。基于该方法进行灵敏度分析，并通过数值仿真观察研究热线半径、测点位置、加热功率、试样半径对热导率估算结果的影响规律。

1 参数估计

1.1 数学模型

熔化示意图如图1所示。该物理模型由半径为b的圆柱形固相PCM和位于圆柱体中心半径为a的线源组成，初始温度T0均匀且低于相变温度某一值(∆T=Tm−T0)。假设t=0 时，恒定的热功率q从线热源中释放，相变材料吸热并沿径向向外熔化。

在图1中，s(t)表示液体和固体区域之间的相界面位置，为时间的函数。此外，在数学模型中使用了以下假设：

1)热线半径a趋向于0；

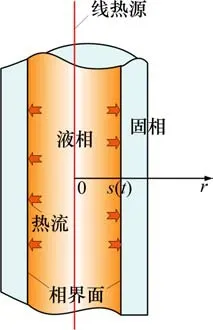
图1 熔化示意图Fig.1 Schematic diagram of melting

2)试样半径b是无限大的；

3)PCM的热特性与温度无关；

4)只考虑热传导。

液相区域控制方程表示如下：

边界条件为：

固相区域控制方程为

边界条件为：

相界面处能量方程为

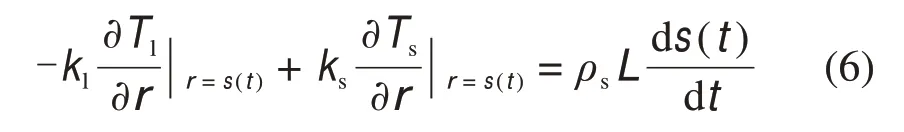
系统初始条件为：

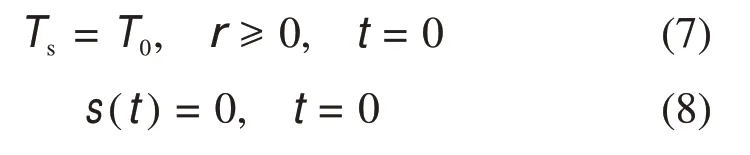
式中：下标l和s分别表示液相和固相；T，T0和Tm分别为温度、初始温度和相变温度，K；k为热导率，W/(m·K)；α为导温系数，m2/s；ρ 为密度，kg/m3；r为监测点位置，m；L为相变材料的潜热，J/kg。

此相变问题的解析解可以在Carslaw 模型[19]中找到，如式(9)和式(10)所示：

式中：E1(x)是一个指数积分函数，定义为

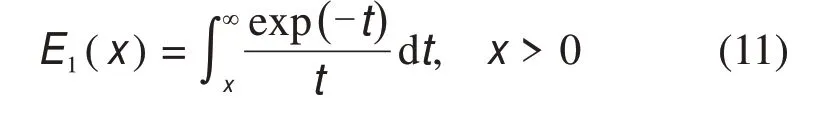
相界面位置随时间变化具有以下关系：

式中：λ为熔化常数，是以下超越方程的根：

1.2 估算方法

采用最小二乘法(OLs)的拟合方法来获得参数：

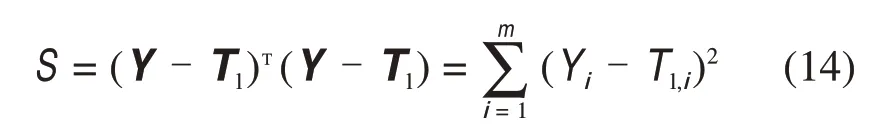
式中：Yi和Tl,i分别为各采样时刻测量及估算得到的液相温度。通过式(9)获得液相热导率kl及熔化常数λ，再代入到式(13)得到固相热导率ks。

使用边界内部信任区域方法来最小化目标函数。边界内部信任区域方法具有二阶收敛属性，该算法可以将估计参数限制在一定范围，因此，它可以避免不切实际的估计。在每个迭代步骤中，内部信任区域方法解决了由二次函数在椭圆约束下定义的信任区域子问题，并收敛到没有输入上限和下限的标准信任区域方法[20]。

1.3 灵敏度分析

相对灵敏度系数Xβ[21]反映参数变化引起Tl的变化，Xβ为

其具体形式为

式中：β为模型方程中的任何参数；Tl,i为时刻ti的第i个Tl观测值(i=1，2，…，n)。方程中的偏导数可用有限差分法进行计算。

本文采用正二十烷作为灵敏度分析材料。表1总结了熔点附近正二十烷的热物理性质，其中热线功率采用10 W/m，监测点位置为距系统中心1 mm处，初始温度为309 K。

表1 正二十烷(C20H42)的热物性参数Table 1 Thermophysical parameters of n-eicosane(C20H42)

图2所示为采用表1中的数据绘制4 条灵敏度系数曲线。从图2可知：灵敏度系数Xαl，Xks和Xαs几乎彼此呈线性相关(3 条曲线彼此平行)。根据BECK 等[22]所得出的结论，这3 个参数在线性相关的范围内不可能都被唯一估计。因此，可将α=k/(ρc)代入方程取代热扩散系数，选取kl和ks作为估算参数。

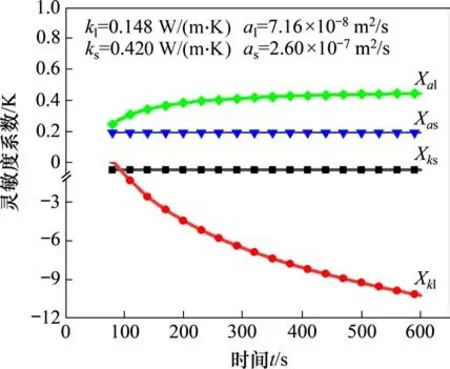
图2 灵敏度系数图Fig.2 Diagram of sensitivity coefficients

2 仿真模拟研究

在上述热导率测量及估算方法的基础上建立数学模型，采用Fluent进行数值模拟得到温度场分布及监测点温度，根据测量方法的原理选取不同的热线半径、测点位置、加热功率及试样半径，得到不同参数对热导率结果的影响规律。

2.1 控制方程

采用焓−孔隙率方法来模拟PCM 的熔化过程，因为该方法控制方程与单相方程相似，并且在固液界面不需要满足显式条件，因此，可以更容易地解决相变问题[23]。连续性方程为

在焓法中，固相和液相的控制方程都是相同的，能量守恒以总体积焓和温度表示，以保持恒定的热物理性质：

式中：H为总体积焓，是显热和潜热的总和：

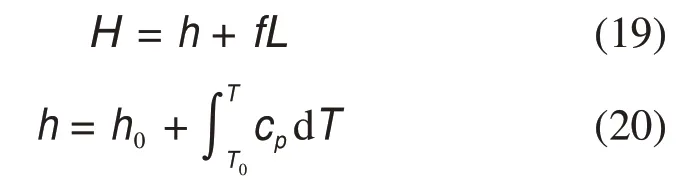
式中：h0为在T0处的显热；cp为比定压热容；f为液体分数，表示液体形式的单位体积分数，与方程式(21)相关。糊状区域是其中液体分数介于0 和1之间的区域。

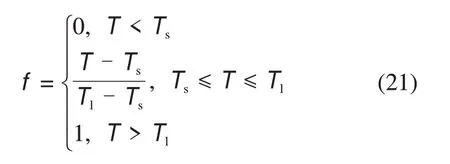
2.2 物理模型建立及验证

采用二维瞬态轴对称计算模型(如图3所示)，使用ANSYS-Fluent 软件求解与相变焓模型相结合的控制方程。选择半径为b、高度为h的固体二十烷相变材料作为案例研究，在对称轴处放置了半径为a的铂丝作为热源。表2所示为所采用铂的热物理性质。系统在顶面和底面上绝缘，而介质的径向外边界保持在初始温度T0。固体块初始时处于均匀的温度T0(低于熔点温度∆T=Tm−T0)，当t=0时，以恒定的加热功率在特定时间段内从铂丝导线向外释放热能。

为了在相变条件下针对Carslaw模型的解析解验证Fluent 模型的准确性，使用ANSYS-Fluent 在相同的初始条件和边界条件下进行案例研究。模型验证采用NABIL 等[12]报道的THW 相关仿真参数，分别选择加热功率和加热持续时间为1 W/m和1 s。计算时间步长为10 μs，每个时间步长最大迭代次数为500(观察迭代次数基本为10左右)。热线半径为10 μm，系统径向长度为20 mm，沿竖直方向长度为5 mm。用于在热线和固相介质中网格的径向划分元素数分别为5 和2 000，几何膨胀比分别为1.050 和1.005，竖直方向上均匀划分为500个元素。经反复验证，计算结果与网格数无关。

图3 二维轴对称模型图Fig.3 Diagram of two-dimensional axisymmetric model

表2 金属铂(Pt)的热物性参数Table 2 Thermophysical parameters of platinum(Pt)

从Carslaw 模型和Fluent 模型获得的导线表面温升随加热时间(即1 s)的变化如图4所示。由于r=0是Carslaw 模型[19]中的奇异点，因此，选择r=1 μm处的位置作为替代导线表面上的位置以获得温升结果。从图4可知：2 个模型预测的温升曲线的趋势非常相似，观察到的偏差小于0.5%。

图4 模型验证对比图Fig.4 Model verification comparison diagram

3 结果和讨论

3.1 热线半径a及测点位置r影响

在Carslaw 模型中，假设热线半径趋近于0，然而实际研究中，所用热线具有一定的热容和半径，因此，开始施加功率时，热流先对热线进行升温才会传递到相变材料中。除此之外，当热线附近材料熔化为液相时，热线表面温升状况会受到热线本身影响，因此，应在距离热线一定距离作为温度监测点。图5所示为模拟纯导热条件下不同热线半径下各监测点的温升状况，其余条件与验证模型相同。

从图5可知：在不同热线半径下，各监测点的温升结果与理论模型的理论计算值的吻合度不同。在线热源功率为10 W/m的条件下，热线半径为a=0.01 mm(图5(a))在监测点r=1 mm 处的熔化所需时间与理论模型计算时间较为吻合，但熔化后整体温度低于理论值；当热线半径为a=0.5 mm 时(图5(f))，监测点r=1 mm 处熔化时间小于理论模型计算时间，熔化后前期温度高于理论温度，但随着熔化时间进行，两者温差逐渐减小，呈现出后期低于理论计算值的趋势。

上述结论也可通过分析数值模型得到，如图6所示，当线热源开始加热时，由于热线具有一定的半径a，热量直接从热线表面传出，达到监测点的路径(r−a)及所需熔化的相变材料与理论模型从半径为0处释放热量相比要小，但热线本身具有一定热容，会使的热线表面温升相对较慢，相同的线热源功率在较大半径热线产生的单位体积功率要比较小半径热线的小，释放出来形成的热驱动力也相对较小，因此，当热驱动力减小的影响程度较小时，加热前期会出现热线半径监测点所需熔化时间基本一致的情况(图5(b)～5(e))，但由于半径增大距离减少的原因，加热后期较大半径的监测点温度要高于较小半径的；而当热线半径增大到一定程度时，热驱动力虽一定程度减小，但热线表面与监测点距离过近，导致温升情况如热线半径为a=0.5 mm 时一般，熔化所需时长减少，但由于热驱动力减小，监测点温度随着熔化时间发展趋势与较小半径(a=0.4 mm)温升趋势相比较为平缓。

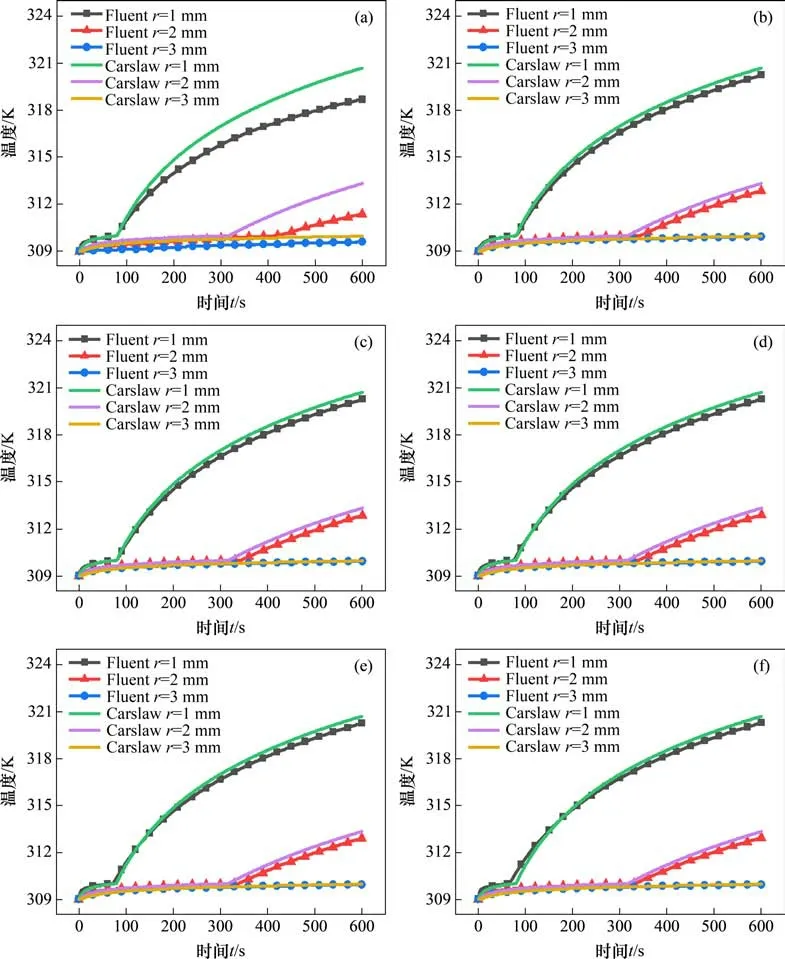
图5 不同热线半径的监测点温升图Fig.5 Temperature rise diagrams of monitoring points with different hot-wire radius

对不同热线半径热导率估算结果如图7所示，与传统瞬态热线法不同，本研究选取高于相变温度某一温差段作为估算结果。从图7(a)可以看出：随着估算初始温度(熔化时间)的增加，液相热导率估算值逐渐减小，精度逐渐增加，这与前面液相热导率灵敏度系数绝对值随观察时间逐渐增加的分析结果一致；与之不同，固相热导率灵敏度系数基本保持不变，且绝对值较小，随着监测点温度与理论值温差逐渐增加，将会导致如图7(b)所示的固相热导率估算值误差增大的现象。

对于监测点位置而言，观察图5(a)～5(f)可以发现，随着监测点位置逐渐远离系统中心处(r=2 mm和3 mm)，其监测到熔化的温升趋势与近监测点(如r=1 mm)同时刻相似，其相关分析结果以线半径a=0.1 mm 为例，估算得到在r=2 mm 处T=311 K时的液相热导率为0.153 W/(m·K)、固相热导率为4.96 W/(m·K)。可知，监测点距离中心轴越远，熔化时间越长，由于相应灵敏度变化的关系，液相热导率精确度相对提高；但由于与理论值温差变大，固相热导率结果误差变大。

图6 不同热线半径传热分析图Fig.6 Heat transfer analysis diagram with different hotwire radius

图7 不同热线半径热导率估算结果图Fig.7 Estimation result diagram of thermal conductivities with different hot-wire radius

3.2 热线功率q及试样半径b影响

图8所示为功率对比图。以热线半径a=0.1 mm在监测点r=1 mm处的温升情况为例进行分析，选取线热源功率分别为5，10 和15 W/m 计算观察，如图9所示。由图9可知：尽管功率的增加可以提高同一时刻的参数灵敏度，但较低功率达到相同估算温度所需时间更长，根据前面液相热导率灵敏度绝对值随着时间增加的规律，在相同估算温度时，较低功率条件下的液相热导率精度要比较高功率条件下的高；与之不同，固相热导率灵敏度不随时间变化，较高功率条件下的固相热导率精度要比较低功率条件下的高。

图8 功率对比图Fig.8 Power comparison diagram

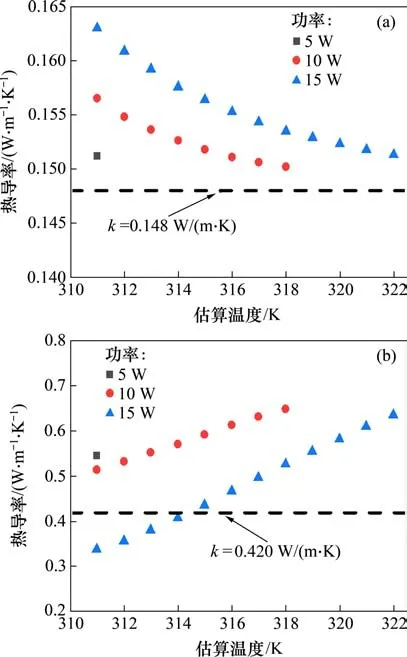
图9 不同功率热导率估算结果图Fig.9 Estimation result diagram of thermal conductivities with different power

图10 不同试样半径温升图Fig.10 Temperature rise graphs of different sample radius

图11 不同试样半径时热导率估算结果图Fig.11 Estimation result diagram of thermal conductivities of different sample radius

选取热线半径a=0.1 mm在试样半径b为3，5，10，15 和20 mm 条件下进行参数分析，如图10和图11所示。从图10和图11可知：较小的试样半径会制约监测点的温升趋势，使得热导率结果偏大；随着试样半径的增大，监测点受到的影响也随之减小，当试样半径大于10 mm 时，影响可忽略不计。除此之外，过小的试样半径条件下，监测点温度受边界影响较大，温升曲线发展趋势相对平缓，热导率结果呈现规律也与之相反。