频域注意力机制下的癫痫脑电信号分类

孙红帅,王霞,柳萱,张连超,赵兴杰

(西安交通大学电子与信息学部,710049,西安)

脑电信号是神经细胞的电活动在大脑的总体反映,包含了大量的生理活动与思维活动的信息[1]。在临床医学研究方面,脑电信号的处理可以为脑部疾病或精神类疾病提供诊断的依据。癫痫是一种常见的神经系统疾病,其特征是在部分或整个大脑区域突然出现异常的电活动,存在如棘波、锐波、尖慢复合波等波形的脑电信号,会直接导致中枢神经系统的功能发生短暂障碍。

由于脑电信号长期记录的性质,其分析是一项耗时的工作。当前在临床诊断和监测中,这种分析依然由医生人工进行,效率低且具有主观性[2]。而软件算法的分析处理更为快速且客观,因此癫痫的发作与正常状态的分类研究是很有意义的。

目前研究人员已提出了多种方法来自动检测癫痫发作,这些方法中的分类算法主要有基于人工神经网络、时频分析的分类算法以及模糊聚类、迁移聚类、多视图聚类、多任务聚类等类型的分类算法[3-10]。

当前存在的分类算法中采用的特征主要是癫痫患者脑电信号的时域或频域特征。

应用时域特征的脑电信号分类算法有基于图论的算法、基于神经网络的算法等。Fan等提出了一个基于混沌理论和频谱图理论的描述脑电信号时间动态的框架,通过状态向量表示脑电信号的各个状态,将多变量脑电信号映射到一个n维状态空间,重构状态空间轨迹来描述系统如何随时间演化,采用复杂的网络模型来表示EEG的递归模式,并在此基础上利用频谱图理论特征对时间同步模式进行量化,从模型中构造的递归中提取递归量化分析特征和图论特征[11]。Yuan等利用脑电信号通道间的相互关系,构建了一种新的基于自编码的多视角深度学习模型,通过在训练阶段增加一个通道感知的竞争机制,提出了一个通道感知的癫痫检测模块来关注重要的和相关的脑电信号通道[12]。

应用频域特征的脑电信号分类算法有基于熵变换的算法、基于小波变换的算法等。Marcelo等利用基于频域表示的Renyi熵及其时域变化的Renyi熵和基于奇异值分解的熵作为脑电信号分类特征,对EEG进行时频复杂度测量,提出了一种新的时变复杂度度量方法[13]。Wang等将小波分解与定向传递函数算法相结合,提出一种新的基于小波的定向传递函数方法,用定向传递函数方法计算了EEG的5个子带和全频带的信息流动特征用于癫痫发作的检测[14]。Abhijit等提出了基于经验小波变换的癫痫发作脑电信号检测方法,对多通道的脑电信号进行经验小波变换,确定信号自适应频率尺度下的联合瞬时振幅和频率,然后用KNN、RF、朴素贝叶斯分类器进行了对比,研究了经验小波变换在多变量脑电图信号上的多元扩展[15]。

Aldana等利用小波变换将脑电信号扩展成三阶张量表示,通过典型多元分解(CPD)和块项分解(BTD)得到特征,采用k近邻法、径向基支持向量机和线性判别分析分类器对正常和癫痫发作的脑电信号进行鉴别[16]。Gu等从发作状态的脑电信号中提取癫痫特征,然后对待检测的样本进行小波变换,小波系数反映了所记录的脑电信号与癫痫特征波形的相似性,对小波变换系数矩阵进行数据融合后,可以确定癫痫发作的边界,可以用来检测癫痫特征波形是否存在于脑电信号中[17]。

上述文献中,已有的特征提取算法多是直接应用癫痫患者脑电信号的时域或频域特征,分类正确率较低。针对以上问题,本文提出了将时频域幅值转化为图片作为初始特征,在残差网络结构的深度学习中,提出了一种频域注意力机制,对癫痫脑电信号的时频域幅值进一步提取特征,以提高发作状态和正常状态的脑电信号分类准确率。采用公开数据库PhysioNet中的CHB-MIT Scalp EEG Database数据库对算法进行验证,结果表明:本文算法对正常状态和癫痫发作状态的脑电信号的分类准确率达到98.05%,灵敏度为96.12%,特异性为99.34%,且该算法对于不同测试者的信号样本分类准确率都在97%以上。

1 分类算法及频域注意力机制

本文提出的癫痫脑电信号分类算法主要包括预处理、特征提取和分类3个步骤。其中特征提取又包括短时傅里叶变换、图片化和加入频域注意力机制的ResNet-50训练。本文算法流程如图1所示。

图1 分类算法流程模块图

1.1 预处理

脑电信号属于连续采集的多通道时序微弱电信号,首先需要通过带通滤波器去除噪声,根据脑电信号的生物节律性选择需要的频带。本文针对癫痫疾病脑电信号,希望能尽可能多地保留频域特征,滤波器通带选择为0～0.5fs。其中fs为采样频率。

在特征提取之前,每2 s截取一段信号作为一个样本。设脑电采集的电极通道数为N,则每一个脑电信号样本为N个长度为2fs的序列。

对每一个序列进行中心化,表达式如下

x′(t)=x(t)-μ

(1)

式中:x(t)为中心化前的序列;x′(t)为中心化后的序列;μ为该序列的均值。

1.2 特征提取

1.2.1 短时傅里叶变换与图片化 为展现信号样本在时频域的状态,需对信号进行短时傅里叶变换(STFT)。脑电信号是一种非周期的无限长序列信号,设为f(t),由于直接对信号截断会产生信息丢失,所以在STFT中,窗函数选择汉明窗,设为g(t),该窗的幅频特性主要表现为旁瓣较小,更容易对信号在样本上进行时域上的分割。f(t)g(t)在不同的有限时间宽度内是平稳信号,从而计算出各时刻的功率谱。

对一个脑电信号样本进行STFT变换后,原数据变为N个时频域矩阵,其中元素为复数,N为采集脑电信号的电极通道数。时频域矩阵中行元素之间代表时间顺序,列元素之间代表频率顺序。将时频域矩阵中元素取模值,得到实数矩阵。将该矩阵变为图片,横轴为时间顺序,纵轴从上到下为频率,顺序从小到大,颜色代表本通道脑电信号在该时段该频率的幅度大小,颜色越亮表明幅度越大。

每个脑电信号样本由N个时序信号组成,经过预处理转化为N个表示时频域特征的图片,以此来表示该信号样本。将N个表示时频域特征的图片作为一组特征输入添加了频域注意力机制的ResNet神经网络,以进一步提取特征并分类。

1.2.2 ResNet残差网络 本文算法将癫痫患者脑电信号的时频域幅值转化为图片做样本特征,因此选择一种用于图片分类的深度学习神经网络来作为网络框架。

He等提出了一个残差学习的框架,以有效减轻神经网络学习训练的压力和负担[18]。该框架将输出层定义为根据输入来学习残差函数,而不是直接学习目标函数。

文献[18]指出,对于一个多层网络,当其输入特征为x时,其学习所得到的特征标记为H(x),可以通过网络学习得到特征残差F(x)=H(x)-x,从而得到其实原始的学习特征H(x)=F(x)+x。残差网络的学习流程如图2所示。

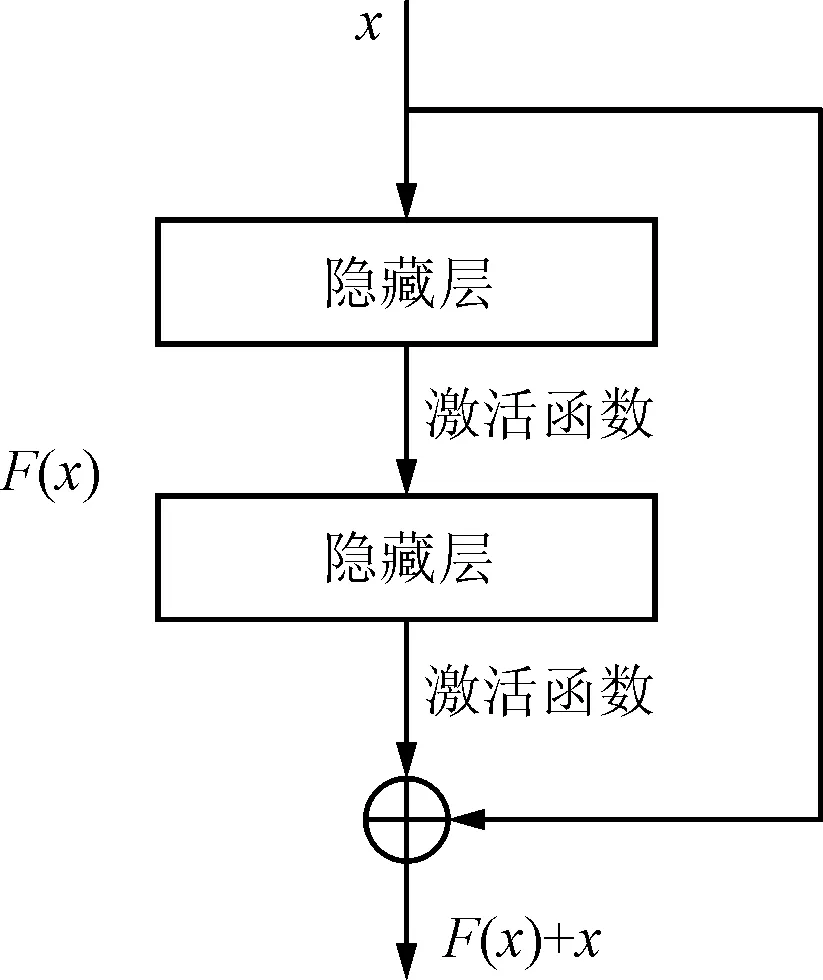
图2 残差网络的学习流程示意图

鉴于ResNet神经网络在图像分类中优异的表现,本文采用其中ResNet-50结构对脑电信号的时频域特征图组进行提取特征并分类。

该网络中损失函数选用交叉熵损失函数。在样本二分类的情况下,模型最后需要预测的结果只有两种情况,对于每个类别,预测得到的概率为pi和1-pi。此时损失函数的表达式如下

(2)

式中:li为样本i的标签,发作状态为1,正常状态为0;n为样本数;pi为样本i预测为发作的概率。

1.2.3 频域注意力机制 该注意力机制即卷积网络通过多个共享卷积核提取具有局部感受野的空间信息和通道信息。在网络中添加注意力机制可以有效地提高网络的表达能力。目前主要有两种添加注意力机制的方式:空间注意力机制和通道注意力机制。通道注意力机制是在卷积网络不同通道间添加注意力机制。空间注意力机制是在卷积网络的空间域内添加注意力机制,例如借鉴非局部均值方法的Non-local Neural Networks网络结构。

目前存在的注意力机制都是以正常图像作为处理对象,来进行特征增强。本文处理的图像中的元素是存在现实物理意义的时域和频域,因此处理普通图像的注意力机制并不适合本文中提取的脑电信号时频域特征图。

本文提出一种针对频域的注意力机制。该频域注意力机制模块在ResNet神经网络中每一个残差学习模块结束时加入,增强频域的特征。

设残差模块输出的特征矩阵为w行h列的特征矩阵Y,如下式所示

(3)

由于STFT后的时频域矩阵中行代表时域,列代表频域,卷积后相对位置不变,在Y中列向量依然可以视为在频域的特征。

设Y中每一个列向量y为式(4),引入频域注意力机制的计算如式(5)所示

y=[y1,y2,…,yw]T

(4)

(5)

频域注意力机制的计算原理如下。

(1)计算列向量y的自相关矩阵M

(6)

(7)

式(7)中,yiyj表示这两个频率的幅值的相关性,对Me矩阵的行求和得到的列向量代表该频率在整个频域中的重要程度,该列向量可作为权重与原特征数据相乘,引入ex使权重能与原特征数据非线性相乘,并且权重越小,经过神经网络层的加深,该频率的权重越靠近0。

(8)

(3)对式(8)矩阵中的行求和得到

(9)

(10)

(6)特征向量的加权式如下

(11)

1.3 识别分类

脑电信号样本经过ResNet-50神经网络最后一个残差模块后,输出的特征为1×2 048维特征数据向量,经过全连接层后,输出样本为两种分类的可能性,再经过softmax层输出最终的分类判断。

2 实验过程及结果

2.1 实验数据

本文的实验数据来自于网络上免费公开的生物信号数据库PhysioNet,选用了其中的CHB-MIT Scalp EEG Database数据库。该数据库收集于波士顿儿童医院,由顽固性癫痫患儿的脑电信号记录组成。该数据库包含22个患者的脑电信号,每个患者的脑电信号监测总时长为30 h,分别保存在15个文件中,每个文件时长为2 h。在监测期间每个患者都出现了癫痫发作的状态。

信号采样频率fs为256 Hz,每个信号样本包含23个通道脑电的信号。这些记录使用了国际10-20脑电图电极位置和命名法。

本文以2 s时长为一个样本,将正常状态下和发作状态下的脑电信号分别分段为独立样本。每个样本为23×512维的矩阵。

2.2 实验过程

本文对频域注意力机制加入前后的效果进行了对比实验,实验过程如下。

2.2.1 信号预处理 预处理是对数据库中的脑电信号进行去噪。由于本文对脑电信号特征提取时,要保留全部大脑活动时的脑电频率特征,因此选择0～0.5fs的低通滤波器对脑电信号滤波。

正常状态样本和发作状态样本中FP1-F7通道的脑电信号如图3所示。

(a)正常状态

2.2.2 短时傅里叶变换并图片化 对样本中每个通道的信号进行STFT,选择汉明窗作为窗函数,设置输出的时频域矩阵中行代表时域,列从上到下为0～128 Hz的频率,每个元素为该信号在对应时段对应频率的幅值。本文实验在脑电信号频域特征选择的频率为0～128 Hz。窗函数长度应该大于等于128,本实验中窗函数长度选择为128。本文STFT采用重叠50%的方法滑动窗函数,所以对于每个样本分为7段。所以每个样本中的一个信号经过短时傅里叶变换后,计算得到的时频域矩阵维数为128×7维。每一个样本有23通道脑电信号,共生成23个128×7的矩阵。

在图片化过程中,需要将时频域矩阵中的元素取模值变为实数。ResNet神经网络处理的图片为方阵,所以对原矩阵右侧补0,生成128×128的方阵。

为直观观察时频域矩阵模值图片化得到的图片,将多个矩阵连在一起生成效果图。癫痫患者正常状态和发作状态FP1-F7通道的脑电信号样本对STFT矩阵取模值后变换得到的图片如图4所示。

(a)正常状态

由图可知,正常状态下,脑电信号在全频段的幅度都有较高幅值的出现,而发作状态下,脑电信号只在低频带的幅值比较高。

通过观察得知,对STFT生成的时频域矩阵取模值生成的图片在正常状态和发作状态具有区分性。

2.2.3 实验结果 设N表示测试集中正常状态样本个数,P表示测试集中异常状态样本数,NT表示测试集中正常状态分类正确的数量,NTP表示测试集中异常状态样本分类正确的个数,分类准确率为Ac,灵敏度为Se,特异性为Sp,则分类准确率、灵敏度及特异性的计算公式如下

Ac=(NTP+NT)/(P+N)

(12)

Se=NTP/P

(13)

Sp=NT/N

(14)

为保证分类器不会对其中一类过拟合,实验中两类样本的数量接近1∶1,其中80%分为训练集,20%分为测试集。

本文算法在CHB-MIT数据库的数据下运行结果如图5所示,图中本文算法为加入频域注意力机制后的算法,ResNet-50表示未加入频域注意力机制的算法,对比算法1为Muhammad等提出的基于动态模式分解的头皮脑电图癫痫发作检测算法[19],主要应用信号的时域特征,对比算法2为Nhan等提出的利用生成对抗网络预测癫痫发作算法[20],主要应用信号的时频域特征。

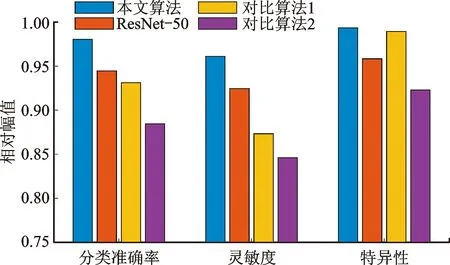
图5 不同算法的分类结果对比

本文算法的分类准确率与训练次数的关系如图6所示。

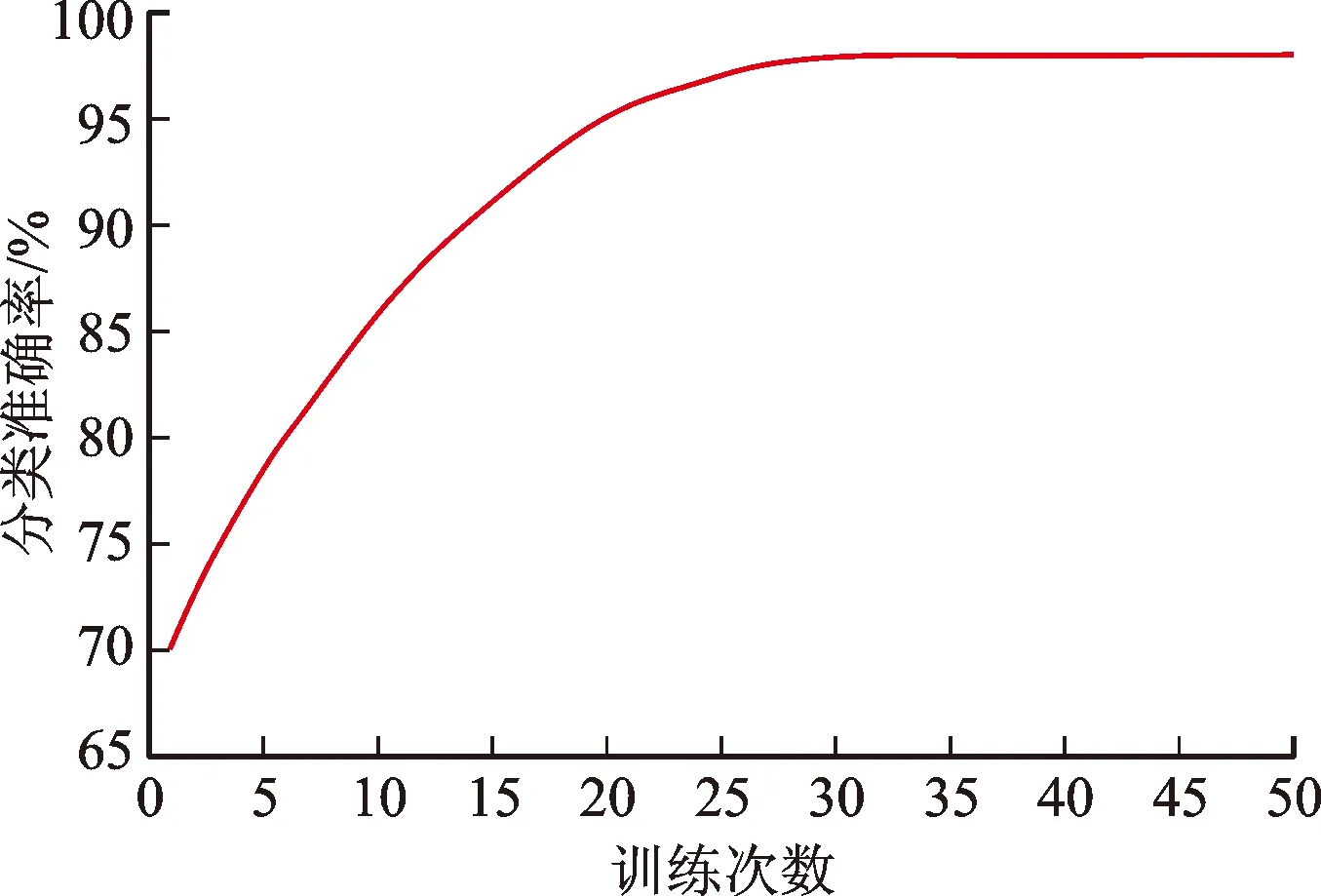
图6 分类准确率与训练次数关系图

2.3 实验分析

由图5结果可知,本文提出将脑电信号短时傅里叶变换后的时频域特征图片化,作为区分癫痫病人正常状态和发作状态脑电信号的特征,用ResNet神经网络进一步提取特征并分类,能达到很高的分类正确率,高于另外两种直接应用时频域特征的算法。

再加入本文中提出的频域注意力机制,能进一步提升算法的分类性能,分类准确率达到98.05%,灵敏度为96.12%,特异性为99.34%。

3 结 论

癫痫疾病的脑电信号异常的特征分布在频域幅值中,为了使提取的特征集中在对分类结果相关性更大的频域中,增强该类频域的幅值特征,并降低与分类结果相关性较小的频域幅值特征,本文基于残差网络结构的深度学习,将时频域幅值转化为图片作为初始特征,提出了一种频域注意力机制,提高了发作状态和正常状态的脑电信号分类准确率,并进行了实验验证。

实验数据为公开数据库PhysioNet中的CHB-MIT Scalp EEG Database数据库,实验结果表明,本文算法对正常状态和癫痫发作状态分类准确率达到98.05%,灵敏度为96.12%,特异性为99.34%。