透平末级叶片材料抗水蚀特性的数值研究

2021-02-22邸娟王顺森蒋希航颜晓江周伟

西安交通大学学报 2021年2期

邸娟,王顺森,蒋希航,颜晓江,周伟

(1.太原科技大学机械工程学院,030024,太原;2.西安交通大学能源与动力工程学院,710049,西安;3.纽约州立大学石溪分校机械工程系,11794,美国纽约;4.中南大学轨道交通安全教育部重点实验室,410075,长沙)

火电和核电凝汽式汽轮机的末级叶片长期工作在湿蒸气区,在运行过程中常常遭受严重的水滴冲蚀。冲蚀不仅会导致叶片的气动性能恶化,降低级效率,而且威胁汽轮机的安全运行,是目前亟需解决的关键问题。随着汽轮机末级叶片发展得越来越长,如不采取有效措施,水蚀现象将变得更严重。

目前常用的防水蚀措施主要为2种:主动式和被动式防水蚀。主动式防水蚀是指从汽轮机结构设计方面减少有害水滴的产生。被动式防水蚀是指采用更抗水蚀的叶片材料或针对叶片易水蚀的区域进行强化。被动式防护的核心问题为高速固液撞击引起的材料损伤。研究高速液固撞击机理可为提高叶片水蚀防护能力提供关键性的意见或建议。关于汽轮机叶片水蚀及高速液固撞击问题,国内外许多学者进行了大量研究。

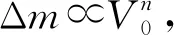
在数值模拟方面,国内外许多研究者尝试利用基于有限元的数值方法来讨论材料的水蚀问题。数值方法不仅能够灵活便捷地针对不同因素(如材料类型、颗粒速度、尺寸、形状和冲击角等)的水蚀行为进行模拟,而且可以大大节约试验周期和成本。Mabrouki等使用任意欧拉-拉格朗日耦合方法(ALE)对弹塑性材料铝合金(A2024T3)进行了数值模拟分析,模拟结果很好地展示了撞击过程中射流和靶材的运动[11]。Haller等着重模拟了速度为500 m/s,直径为200 μm的液滴撞击刚体平面的过程,阐述了撞击过程中液体的压缩过程、激波的传递过程及侧向射流的产生[12]。Ma将有限元法和光滑粒子流体动力学(SPH)方法相结合,研究了高速水射流冲击靶材的过程并描述了水蚀机理;通过与试验结果的比较,证明了该耦合方法的有效性,并比较了有限元耦合光滑粒子流体动力学方法和ALE方法,指出在相同计算精度条件下,有限元耦合光滑粒子流体动力学方法比ALE方法更节省计算资源[13]。Hsu等使用耦合拉格朗日-欧拉法(CEL),模拟了速度为570 m/s的水射流撞击PMMA靶材的过程,发现数值模拟结果与试验结果吻合,且数值模拟对试验难以得到的细节做了很好的补充[14]。汪勇等通过SPH耦合有限元算法(FEM)模拟计算了高速液滴撞击PMMA的过程,指出撞击后产生的高速侧向射流是固体发生破坏的主要原因,同时对撞击过程的激波动态结构进行了分析,得到了撞击过程中压力分布的合理解释[15]。

综上所述,目前已有很多学者针对液固撞击过程进行了大量理论、试验和数值研究。总体而言,由于水蚀过程的复杂性,加之其在不同靶材和不同水蚀环境下的差异性,因此对材料水蚀规律和机理还缺乏深入的理解,如靶材表面形貌在水蚀过程中的演化特征,水蚀失效模式及不同表面强化工艺影响其抗水蚀性能的内在深层原因,材料表面粗糙度、射流速度及角度对水蚀性能的影响等。本文基于FEM-SPH耦合算法,分析射流角度、射流速度及材料表面粗糙度对汽轮机典型末级叶片基材17-4PH抗水蚀性能的影响,有助于进一步理解叶片材料水蚀规律,指导工艺参数优化。

1 液固撞击理论和数值方法

1.1 液固撞击理论

Cook[16]假定被撞击固体是刚体并且撞击是一维的,在此情况下,根据能量守恒原理,液体在撞击前的动能转化为液体的压缩能,由此可推导出“水锤”的压力公式为

P=ρ0C0V0

(1)

式中:P为液体撞击固体所产生的撞击压力,即“水锤”压力,Pa;ρ0为未受扰动时液体的密度,kg/m3;C0是未受扰动时液体的声速,m/s;V0为射流速度,m/s。

由式(1)可知,撞击产生的压力在发生撞击之后会急速下降,这是因为在这之后从撞击区域向液体和靶材中释放了压力波。如果撞击持续进行,由伯努利方程可推得,撞击压力将会达到一个稳定值。平稳阶段的撞击压力为

(2)

(3)

(4)

其中k为考虑液体性质的常数,在液体是水的情况下取2。

考虑到在数值计算中通常采用三次方关系的激波关系式[18-19],它比Heymann线性拟合的关系式(3)准确度高,因此之后在讨论水锤压力理论值时都用激波三次方关系式计算得出的数值,即

(5)

1.2 计算模型

图1是水柱射流冲击靶材的计算模型,取射流直径为0.15 mm,射流高度为1 mm。射流与靶材之间取间隔距离为0.1 mm,以防止在计算前模型有初始穿透。设置靶材长、宽均为1 mm,高度为0.3 mm。将固体靶材底面完全约束,并在其底面和4个侧面上施加无反射边界条件以模拟无穷大平板的射流撞击过程。

为与高速水柱射流冲击试验条件匹配,射流参数选取和试验条件一致,如表1所示,具体试验参数及试验步骤见文献[20-21]。采用17-4PH作为靶材材料,射流速度取为650 m/s,靶材在试验过程中绕轴旋转,轮盘转速n0为1 500 r/min,根据式(6)计算其在碰撞点的旋转线速度为

Vr=wr=2πn0r

(6)

式中:r是与碰撞点射流相对应的圆盘半径。本试验中r=144 mm,求得旋转线速度Vr≈22.62 m/s。

表1 模拟采用射流参数

在数值模拟中,将靶材的旋转速度等效为22.62 m/s的平动约束,计算时间为2.3 μs。通过在靶材表面开设6个凹槽结构的方式模拟靶面初始粗糙度,凹槽深度分别为2 μm和10 μm,见图2。本文共模拟计算了4个角度射流撞击靶材的过程。

1.3 物性参数及边界条件

考虑到汽轮机末级的实际工作环境,将试验箱体内气压设置为0.1～0.15个大气压,故可认为射流从喷嘴中喷出后空气对其影响很小,在模拟过程中忽略空气的存在,仅考虑水柱射流和固体靶材的相互作用。

(a)2 μm凹槽90°模型图

本文选用马氏体基材17-4PH作为靶材,对其进行高速水柱射流水蚀模拟。靶材的本构模型选用随动塑性材料模型,具体材料参数如表2所示。

表2 靶材的材料参数

由于水滴在撞击时压力较高,受到较大压力,因此需考虑其压缩性。采用Mie-Gruneisen状态方程[19]描述水在撞击过程中的状态。试验中射流由蒸馏水箱中经过高速射流发生器产生,故考虑其温度为室温。水射流采用常温常压下的物性参数。水的初始物性参数按标准大气压下20 ℃时选取,C为Us-Up曲线(冲击波速度Us和质点速度Up曲线)的截距,即当地声速;γ0为Gruneisen常数;μ为水的动力黏性系数,取1.002×10-3Pa·s;a是γ0的一阶修正系数;S1、S2、S3为Us-Up曲线的斜率系数,也称为水状态方程系数。水的物性参数和Mie-Gruneisen状态方程参数见表3[19]。

表3 水的物性参数和Mie-Gruneisen状态方程参数[19]

1.4 模型验证

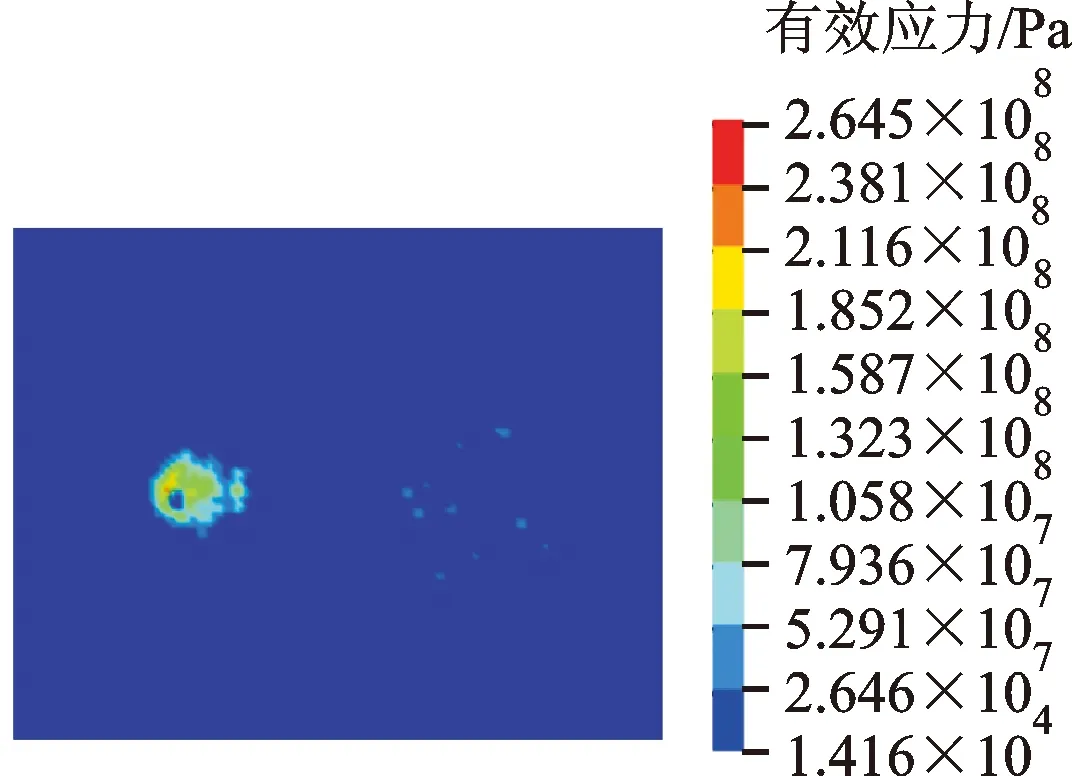
水柱射流冲击刚性靶材的初始冲击压力P为1.954 GPa,如图3所示。与理论水锤压力相比,计算误差为5.4%,在误差允许范围内。

图3 水射流垂直冲击刚性靶材的初始冲击压力云图

将靶材材料设置为刚体,在保证SPH粒子均匀分布的情况下,逐渐增加粒子密度,直到粒子撞击靶材过程中撞击压力网格无关。最终选择的SPH粒子密度为每层209个,共107层。确认SPH粒子密度后,将靶材网格密度从长×宽×高为150×150×15增加到320×320×32,计算所得初始撞击压力随网格密度的变化如图4所示。从图中可以看出,网格划分大于240×240×24以后初始撞击压力趋于稳定,300×300×30时初始撞击压力为1.954 GPa,320×320×32时初始撞击压力为1.96 GPa,相差0.31%,可认为靶材网格无关,取网格尺寸为300×300×30。有限元模型的网格拓扑关系见图5,采用三维六面体8节点实体显式单元solid164对靶材进行划分网格。

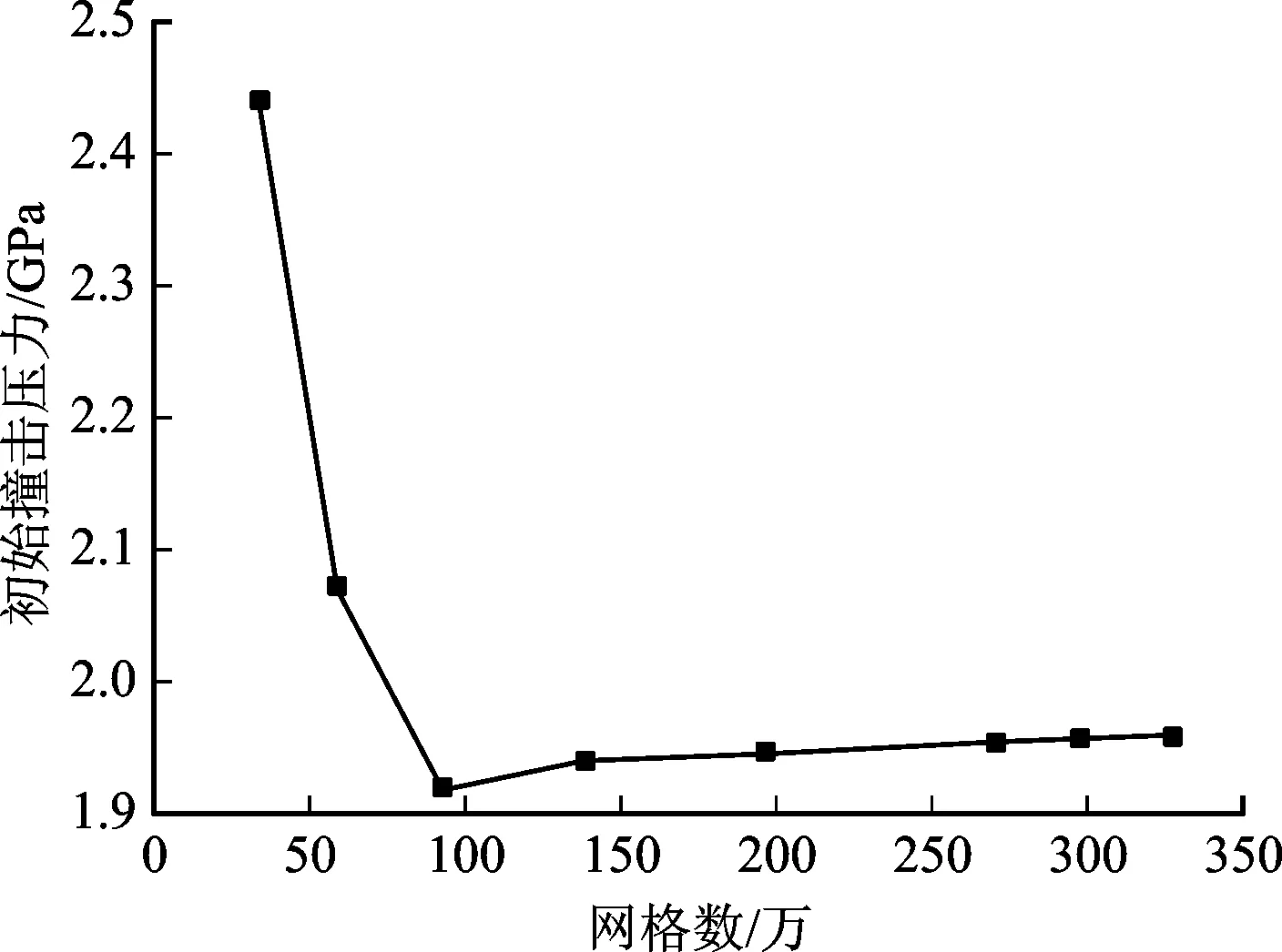
图4 初始撞击压力随网格密度变化曲线

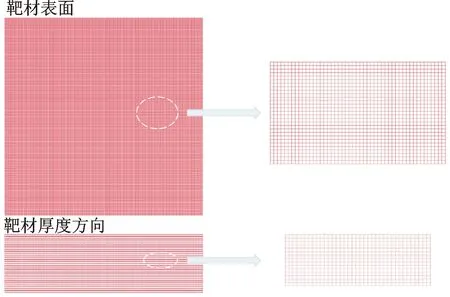
图5 有限元模型的网格拓扑关系图(放大倍数约为5)

2 数值计算结果与分析

图6以30°水柱射流撞击10 μm凹槽靶材为例,选取6个典型时刻展示水柱射流过程。

(a)0 μs

从图6可以看出,水柱与靶材发生初始接触时并不会产生碰撞,需要射流继续向前运动与靶材相互作用才会开始碰撞过程。水柱与靶材碰撞瞬间,没有产生侧向射流,水柱前端为压缩状态。随后靶材表面应力呈环状由撞击中心区域向外部区域传播,水柱射流在发生初始撞击后出现侧向射流,且撞击后由撞击表面产生压力波向射流内部传播,应力最大值出现在射流水柱外圈与靶材接触的环状区域。随后不再有新的高应力区出现,之前产生的应力波继续向靶材内部传播。随着射流继续撞击靶材,靶材表面逐步被破坏,形成冲坑。

图7为不同粗糙度(光滑靶材、2 μm及10 μm凹槽)靶材内部最大有效应力随冲击过程的变化,可以看到,2 μm和10 μm凹槽靶材内部最大有效应力最终均稳定在730 MPa附近,而光滑靶材内部最大有效应力最终稳定在280 MPa左右,比带凹槽结构靶材的最终稳定应力小得多。

图7 不同粗糙度光滑靶材内部最大有效应力随冲击过程的变化

(a)光滑表面30°冲击

2.1 表面粗糙度和射流角度对水蚀的影响

(a)2 μm凹槽30°冲击

(a)10 μm凹槽30°冲击

图8～图10分别为光滑表面、2 μm及10 μm凹槽表面在不同射流角度(30°、60°、80°、90°)水柱射流冲击下,靶材的微观形貌和有效应力(即von Mises应力)云图。可以看出,对于每一种表面结构,90°冲击时形成的冲坑最严重,质量损失也最大,30°射流冲击下试样冲坑最浅,尤其是光滑表面,基材仅冲出非常浅的冲坑;在其他条件相同的情况下,靶材表面粗糙度越大,水蚀越严重;10 μm凹槽试样比2 μm凹槽试样更容易形成冲坑,冲蚀损伤也更严重。即材料表面初始粗糙度越大,水蚀破坏越严重,抗水蚀性能越差。

图11给出了不同粗糙度(光滑表面、2 μm凹槽、10 μm凹槽)马氏体基材的质量损失随水柱射流冲击角的变化。可以看出,随着基材表面粗糙度的增加,水蚀累积质量损失增大,水蚀破坏加剧,且最大质量损失发生在冲击角为90°;10 μm凹槽时基材的质量损失平均为2 μm凹槽试样的1.6倍,2 μm凹槽试样的平均质量损失约为光滑表面试样的1.4倍。90°水柱射流冲击试验中,表面未抛光的线切割基材质量损失平均为其抛光样的1.86倍。结合数值模拟结果,充分说明表面粗糙度对材料水蚀性能影响显著,随着靶面粗糙度的增加,水蚀损伤加剧。Hancox也报道了类似的研究[9]:以18/8不锈钢为研究对象,射流直径为1.3 mm,试样的表面粗糙度从37 μm变为1 μm,测量了表面凹陷形成和材料去除所需的冲击次数,发现当表面粗糙度从12 μm变为1 μm时,水蚀破坏减少了40%。

为进一步分析材料表面粗糙度对水蚀性能影响的深层机理,对不同粗糙度下靶材最大冲击压力进行了统计。图12展示了不同粗糙度的马氏体基材17-4PH的最大冲击压力随水柱射流冲击角的变化。可以看出,材料的最大冲击压力随水柱射流冲击角的增加而增大,当射流角度为90°时,撞击压力最大;随着表面粗糙度的增加,各射流角度下,靶面最大冲击压力升高,靶材质量流失加剧,因此抗水蚀性能较差。基材最大撞击压力与靶面粗糙度的关系,充分说明提高材料表面光洁度能促进水滴压力波的自由扩展,降低材料最大撞击压力可以提高材料的抗水蚀性能。

图12 不同粗糙度马氏体基材的最大冲击压力随水柱射流角度的变化

图13给出了30°射流角度的水柱冲击光滑表面,马氏体基材最大压力随冲击时间的分布。可以看出,靶材最大冲击压力在水柱与靶面的接触瞬间迅速增加,随着射流冲击过程的继续进行,最大压力在250～700 MPa范围内波动,在1.9 μs后,压力最终稳定在200 MPa附近。

图13 光滑表面马氏体基材在30°水柱射流冲击下最大压力随冲击时间的变化

2.2 射流速度对水蚀的影响

以2 μm凹槽粗糙度为例,选择4种水柱射流冲击速度325、418、563、650 m/s分析水柱射流速度对水蚀的影响。

水蚀质量损失Δm和射流速度V0具有以下指数关系

(7)

式中:n为速度指数。使用对数坐标图拟合得到马氏体基材17-4PH速度指数n≈3.83,见图14。从图14中可以看出,射流速度越高,水蚀累积质量损失越大,材料水蚀损害越严重。Ahmad等研究结果显示,对于高屈服强度钢合金,n=3.3～4.5;对于Ti6Al4V,n≈5[4]。本文研究的马氏体基材17-4PH属于高屈服强度钢合金,拟合所得速度指数n≈3.83,与文献[4]报道的结果吻合。