软件定义卫星网络多控制器可靠部署算法
2021-02-22郭子桢梁俊肖楠陈威龙
郭子桢,梁俊,肖楠,陈威龙
(空军工程大学信息与导航学院,710077,西安)
由于传统卫星网络存在可拓展性差、设备难以更新升级、多种协议并存、无法为不同需求的用户提供细粒度服务等问题[1],近年来软件定义卫星网络(SDSN)开始走进研究人员的视野。SDSN采用控制与转发分离的软件定义网络(SDN)架构,通过控制器管理整个网络,提高了网络的可扩展性和可编程性[2-3]。低轨道(LEO)卫星星座作为卫星网络转发平面的主要组成部分[4-5],如何高效地对其进行管理是SDSN的核心问题之一。不同于地面SDN网络,LEO卫星拓扑高速动态变化、业务时空分布不均匀,因此需要针对性的进行控制器的部署。
Wu等建立了SDSN开销模型,以开销为优化目标,将最差时延作为衡量网络可靠性的指标,却忽略了链路失效、节点失效对网络性能的影响[6]。Hu等提出SoftLEO策略,按轨道将卫星分为6组,挑选6个运动方向相同、纬度相近且由轨道间链路相连的节点部署控制器[7],保证了网络的时延性能,但对可能的节点失效及链路失效缺乏考虑。Xu等的部署方法与SoftLEO类似,不过为避免卫星进入两极地区时对控制器间通信的影响而动态地选择赤道附近的卫星节点部署控制器,且控制器的数量增加了一倍[8],同时也欠缺对可靠性的考虑。刘治国等以端到端时延为控制器部署评价指标,但部署模型以管理节点数表征控制器负载,对于业务分布极不均匀的卫星网络难以做到控制器间负载均衡[9]。杨力等通过负载门限判别控制器状态,进而实现负载的动态迁移,然而仿真实验并未基于卫星网络拓扑[10]。Wu等主要关注已有卫星网络的扩展问题,未将网络构建时的控制器部署问题作为研究重点[11]。Papa等以流建立时延为优化目标,部署方案拥有较好的时延性能,但缺乏对除时延外其他网络性能指标的考虑[12]。
现有SDSN控制器部署研究仍存在不足:一是忽略控制器处理时延仅考虑传播时延。这相当于忽视控制器间处理能力差异,默认所有数据包的处理时间都相同。实际上,当控制器处理能力较小时,处理时延也对网络性能有较大影响。二是缺乏对可靠性的考虑。SDN网络的可靠性研究已较多而SDSN控制器可靠部署问题却仍缺乏足够的重视。
本文提出一种SDSN多控制器可靠部署算法,并利用改进的人工鱼群算法进行求解。该算法将处理时延加入控制时延模型以优化网络时延,同时通过定义节点失效概率及链路失效概率衡量网络可靠性。仿真对比说明,MCRDA算法能在保证较小的控制时延的前提下实现控制器间的负载均衡,并使网络可靠性提高30%以上。
1 模型构建
本文主要面向SDN架构下LEO星座中控制器部署问题进行建模,以解决控制器部署位置的选取问题(选择部分LEO节点作为控制器),并建立控制器到交换机间的控制关系[13]。SDSN网络可描述为G=(V,E),构建模型所用参数及其说明见表1。表中xi,j、an均为二进制变量,用于表征交换机-控制器连接关系及控制器部署位置,其取值方法如下
(1)
(2)

表1 网络参数汇总表
在定义其他参数前对模型进行说明如下:控制器可能部署于网络中任意节点上,且位置确定后不可更改;使用时间片划分思想,处理拓扑动态变化的LEO卫星网络[14],并假设在时间片持续时间内网络拓扑、业务、控制器与交换机连接关系保持不变;网络重规划仅在时间片切换时进行。
1.1 控制时延
为使网络能满足不同用户的需求,控制器部署应当使网络中控制器到交换机的响应时间(控制时延)[15]尽量短。卫星网络覆盖范围广,为了减小控制时,要求控制器分布尽量均匀,如果过于集中,则必然造成部分节点控制时延过大。因此,本文定义了最远距离以防止控制器的集中。
定义1最远距离D。D代表交换机与最近控制器距离的最大值,该值较大说明部分节点距离控制器较远,网络中控制器分布比较集中;反之,则说明控制器分布较为均匀。D表达式如下
(3)
现有大部分卫星网络控制器部署研究及地面广域网研究都忽略了控制器处理时延,本文在时延模型中加入了处理时延。
定义2控制时延T。Ti,j表示交换机sj与控制器ci进行一次控制信息交互所花费的时间,其计算公式如下
(4)
式中:右侧第2项为往返路径上的传播时延;右侧第1项为流请求在控制器中处理所需的处理时延;c为自由空间光速。处理时延只与流请求大小及控制器处理能力有关,不同交换机处理时延相互独立。将控制器ci的控制时延Ti定义为ci到其控制的所有交换机的控制时延之和[16]
(5)
Ti值越小则控制器对所属交换机的控制越高效。出于负载均衡的考虑,将整个网路的控制时延T定义为各个控制器控制时延按负载加权的和,qi为控制器ci的负载,计算式如下
(6)
(7)
由定义可知,负载大的控制器对网络控制时延的影响更大。在控制器处理能力相同时,负载大的控制器往往有较大的控制时延,网络中出现过载控制器将严重影响网络的控制时延。因此,负载加权方法在保证网络时延性能的同时也兼顾了控制器间的负载均衡性能。
1.2 控制链路可靠性
控制链路可靠性是规划网络时必须考虑的重要因素。由于卫星网络的栅格化,网络中两个节点间往往存在多条联通路径,因此能够通过控制器选址及控制关系在保证网络时延的情况下尽可能提高控制链路可靠性,使网络更加可靠。本文主要基于概率分析控制链路的可靠性。
定义3直连链路失效概率re。直连链路失效概率由链路长度决定,长链路失效概率更大。re的计算式如下
re=(1-αu)de
(8)
式中:αu为单位长度失效概率;de为直连链路长度。由于轨道间链路和轨道内链路的差别,不同类型的链路应当具有不同的单位长度失效概率。卫星节点在极点附近会关闭其轨道间链路而保留轨道内链路,频繁的开闭使轨道间链路的单位长度链路失效概率应当比轨道内链路更高。
定义4节点失效概率rn。节点失效概率表示网络中节点无法正常行使功能的概率。
定义5控制节点失效概率ξ。在选择控制器时,为了保证网络的可靠性,应当尽量将控制器部署在节点失效概率较小的节点上。ξ的计算式如下
(9)
定义6控制链路可靠系数R。控制链路可靠系数由控制链路上的节点失效概率及直连链路失效概率共同决定,交换机sj与控制器ci间的控制链路可靠系数Ri,j计算方法如下
(10)
ci所属控制域的控制链路可靠系数Ri为控制域内所有控制链路可靠系数的平均值。同样出于负载均衡的考虑,整个网络的控制链路可靠系数R定义为各控制域控制链路可靠系数按负载加权的和,Ri和R计算式如下
(11)
(12)
控制链路可靠系数能够反应网络的可靠性,可靠系数大的网络控制器与交换机之间的连接更不容易中断,发生控制链路失效的概率更小。
定义7节点吸引度λj。λj表示节点vj对控制器的吸引力,控制器更倾向于部署在λj大的节点上。该值由节点失效概率及其所连接的直连链路共同决定,节点连接的直连链路越多、链路失效概率越小、节点失效概率越小,则节点吸引度越大、可靠性越好。λj的计算式如下
(13)
1.3 目标函数
为实现对时延、可靠性等评价指标的综合优化,将SDSN控制器部署目标函数概括如下
(14)
(15)
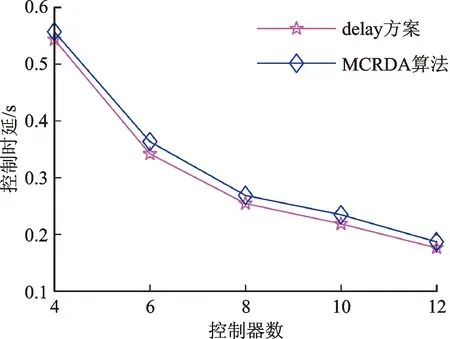
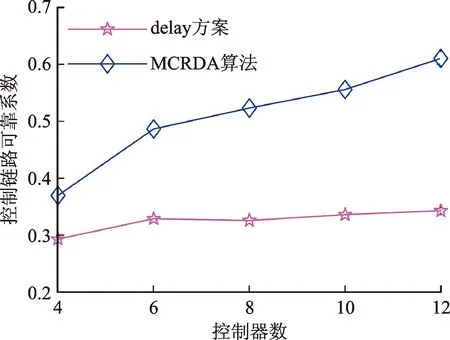
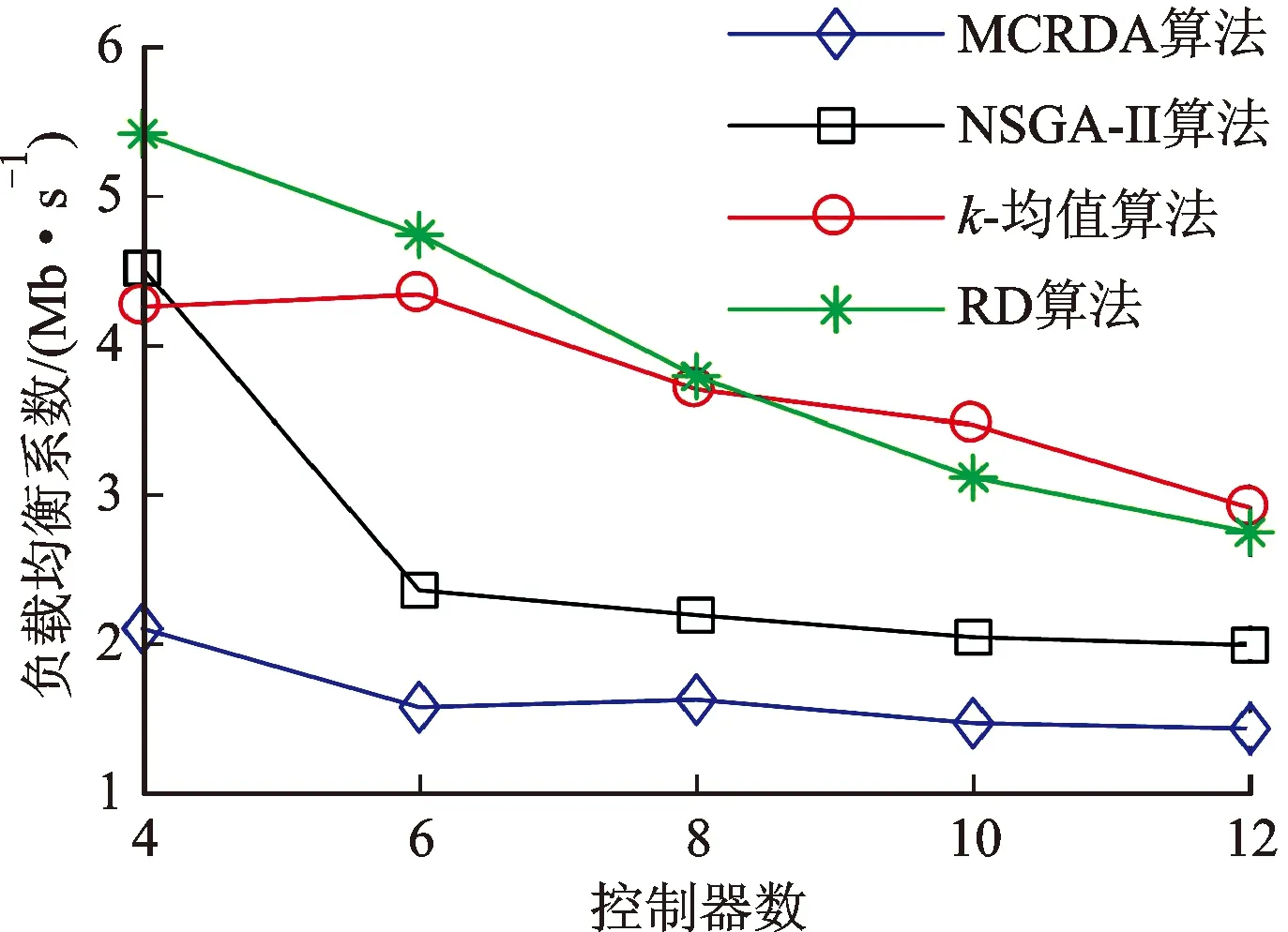
∀i∈C,qi (16) (17) 式(14)第一项为控制器选址优化目标,后一项为控制域划分优化目标。求解时由于两项优化目标难以同时最优,故对第一项优化目标构造非劣解集而主要对后一项进行优化。式(15)表示每个交换机仅受一个控制器控制;式(16)表示控制器负载不能超过处理能力;式(17)表示控制节点平均失效概率应小于所有节点平均失效概率。 控制器部署问题已被证实为非确定性困难(NP-hard)问题[17],而智能启发式算法是求解NP-hard问题的有效手段之一。由于人工鱼群算法具有实现简单、鲁棒性强、对参数选择不敏感、全局寻优能力强、收敛速度快等优点[19],本文利用人工鱼群算法求解SDSN控制器部署问题。人工鱼群算法所用参数见表2。人工鱼群算法中共包括4种行为:觅食行为,鱼群趋于向视野范围内食物浓度高的区域移动;聚群行为,人工鱼趋于聚集成群,在避免拥挤的情况下向邻居伙伴的位置中心移动;追尾行为,当一条人工鱼发现食物后,附近的人工鱼会尾随而来;随机行为,人工鱼随机地在水中自由游动。人工鱼群算法流程如图1所示。 表2 人工鱼群算法参数汇总表 图1 人工鱼群算法流程 经典人工鱼群算法运算时步长固定,若步长过小,算法收敛速度慢,可能无法到达最优解;若步长过大,算法可能在最优解周围振荡而无法准确收敛[18]。因此,为了提升算法寻优能力并加快收敛速度,本文采用指数函数型衰减的步长,步长更新方法如下 (18) 式中:ξmax为最大步长;ξmin为最小步长。在运算前期,步长较大使样本能够快速地接近最优解;在运算后期,步长逐渐减小,使样本能够准确停留在最优解位置[19]。 本文利用改进的人工鱼群算法求解SDSN控制器部署问题的MCRDA算法,具体步骤如下。 输入:SDSN网络G,网络流量,控制器处理能力p,控制器数量M,人工鱼群算法参数 输出:控制器部署位置集合A,控制域划分X 1:采集d、rn、re等网络参数 2:生成初始样本 3:whileβ<βmaxdo 4:更新步长ξ 5: whilek 6: 计算各样本目标函数值 7: 用改进的人工鱼群算法更新样本位置 8: endwhile 9: 构造非劣解集并排除无效解 10:endwhile 11:得到X、A (1)实验平台介绍。仿真实验均利用STK 11.01进行卫星网络拓扑信息的采集,利用Matlab 2016b进行算法仿真以及实验结果处理。 (2)拓扑选择。由于Iridium为最经典的LEO卫星星座且具有星间链路,诸多卫星网络相关研究均将其作为实验拓扑,故以Iridium星座作为本文实验拓扑,具体参数如表3所示。 表3 仿真实验拓扑参数 (3)业务模型。本文所用卫星网络业务流量模型将地球表面划分为288个区域,在每个区域内以106为单位计算该区域的用户数(该用户数为区域内用户总数而不是正在使用网络的用户数)及流量,每个区域的流量由距其最近的卫星节点转发[21]。每组用户的流量情况受当地时间的影响,10时至22时流量达到最大值1 Mb/s,0时至6时最小,具体如下 (19) 需要注意的是,在SDN架构下,不是所有数据包都需要控制器处理,只有无法匹配流表的数据包需要调用控制器处理资源,设这部分数据的比例为10%[12]。由此模型,交换机流请求速率的值即为所有由该交换机负责转发的地区业务流量之和乘以10%。 (4)仿真参数。在LEO星座每个周期内设置6个时间片,将部署方案各时间片内仿真性能的平均值作为方案最终性能,控制器处理能力取60 Mb/s。在0~0.1范围内,差异化地确定各个节点的失效概率,且不同节点的失效概率相互独立。人工鱼群算法中种群数量为400,迭代次数为200,试探次数为50,视野为37,步长范围为5~55,拥挤度因子为0.618。 为了展示MCRDA算法的性能及优势,本文共设计了3组实验。在仿真实验中,除了控制时延与网络可靠性,负载均衡也是反映网络性能的一个重要指标。本文定义控制器负载标准差为负载均衡系数δ,并以此表征网络负载均衡性能,计算方法如下 (20) (21) 图2 控制器节点平均失效概率与控制数的关系 (1)实验1:控制器节点平均失效概率。由图2可知,MCRDA算法选择的控制器节点平均失效概率随控制器数量的增加有增大的趋势,不过仍小于所有网络节点的平均失效概率。这是由于控制器数量较少时,在选择控制器节点时有较大余裕。控制器数量较多时,由于控制时延的约束,一些失效概率较大的节点不可避免地被作为控制器使用,使得控制器节点平均失效概率略微上涨。最极端的情况就是网络中所有节点均部署控制器,此时控制器节点平均失效概率达到最大,等于所有网络节点的平均失效概率。 (2)实验2:考虑可靠性对控制时延的影响。由于控制时延和网络可靠性难以同时达到最优,在优化目标中加入可靠性指标,将不可避免地带来控制时延的下降。由图3~5可知,相较于仅对控制时延进行优化的部署方案(下称delay方案),本文算法能够牺牲较小的控制时延和负载均衡率,换取网络可靠性的较大提升,其中控制时延性能下降不足7.4%,网络控制链路可靠性提升了近50%。这是由于卫星网络的栅格性,使得网络中两个节点间存在多条可能的路径,因此在部署控制器时,通过合理调整控制器的位置能够在控制链路长度相差不大的情况下取得更高的可靠性指数。 图3 两种算法控制时延的对比 图4 两种算法负载均衡率的对比 图5 两种算法控制链路可靠性的对比 (3)实验3:MCRDA算法与其他部署方案对比。k-means算法将节点按照距离划域,并在域中心处部署控制器[22];RD算法随机选择控制器部署位置,并按最短距离原则为控制器分配交换机;NSGA-Ⅱ算法综合考虑网络端到端时延与负载均衡,静态的规划卫星网络[9]。MCRDA算法与其他部署方案性能对比见图6~8。 图6 4种算法控制时延的对比 图7 4种算法负载均衡率的对比 图8 4种算法控制链路可靠性的对比 由图6~8可见,随着控制器部署数量的增加,4种算法的控制时延和负载均衡率均呈现下降趋势,可靠性呈上涨趋势。这是由于,随着控制器数量的增加,网络控制链路长度的减小以及总处理能力的增大。NSGA-Ⅱ算法将端到端时延作为优化目标,导致网络中控制器到交换机的最大时延较大,因而控制链路较长,控制时延与网络可靠性不理想。NSGA-Ⅱ算法虽然加入了对负载均衡的考虑,但却忽略了每个卫星节点流请求数量的差异而追求控制器连接的卫星节点数量的均衡,故其负载均衡性能虽优于另外两种算法却仍与MCRDA算法有一定差距。k-均值算法、RD算法分析时延时忽略了处理时延,也未考虑控制器负载差异对网络性能的影响,故而负载均衡性能较差。不过由于两种算法优先挑选距离短的链路作为控制链路,所以控制链路可靠性要优于NSGA-Ⅱ算法。由于全面的考虑了时延与可靠性,并且在建立模型时加入了对负载均衡的约束,MCRDA算法在控制时延、负载均衡率、可靠性方面均优于对比算法,控制时延提升23%以上,负载均衡率提升25%以上,网络的控制链路可靠性提升约30%。 本实验还进行了MCRDA算法与现有卫星网络控制器SoftLEO、SCSS部署方案的性能对比,如图9所示。 图9 MCRDA与其他卫星网络控制器部署方案对比 由图9可知,在不同控制器部署数量情况下,MCRDA算法各项性能均优于对比方案,尤其是负载均衡性能提升可达53.2%。这是因为,SoftLEO方案与SCSS方案均按照轨道划分控制域,卫星网络业务空间、时间分布的不均匀特性不可避免地导致控制器间的负载差距大。同时,这种部署方式使得控制链路上只包含轨道内链路,不含失效概率较大的轨道间链路,因此这两种方案的控制链路可靠性均较为优秀,不过仍略低与本文算法。值得一提的是,SCSS部署方案要求网络中所有卫星节点均安装控制器模块(同一时刻只有部分节点开启该模块作为控制器使用),同时动态调整控制器的开闭状态以适应网络业务和拓扑的变化,这就使得该算法的设备制造、发射成本巨大,经济效益较差。 本文结合卫星网络特点,同时考虑到链路失效与节点失效,提出了一种SDSN多控制器可靠部署算法,将处理时延加入时延模型以提高网络性能,并利用可变步长的人工鱼群算法求解。仿真结果表明,与现有控制器部署方案相比,MCRDA算法能够在保持良好时延性能的同时,将网络可靠性提升30%以上,负载均衡性能提升25%以上。不过本文仍有以下不足:计算链路失效概率时未考虑流量拥塞,缺乏对控制器间通信的研究分析。这些不足将在未来研究中加以改进。2 求解算法

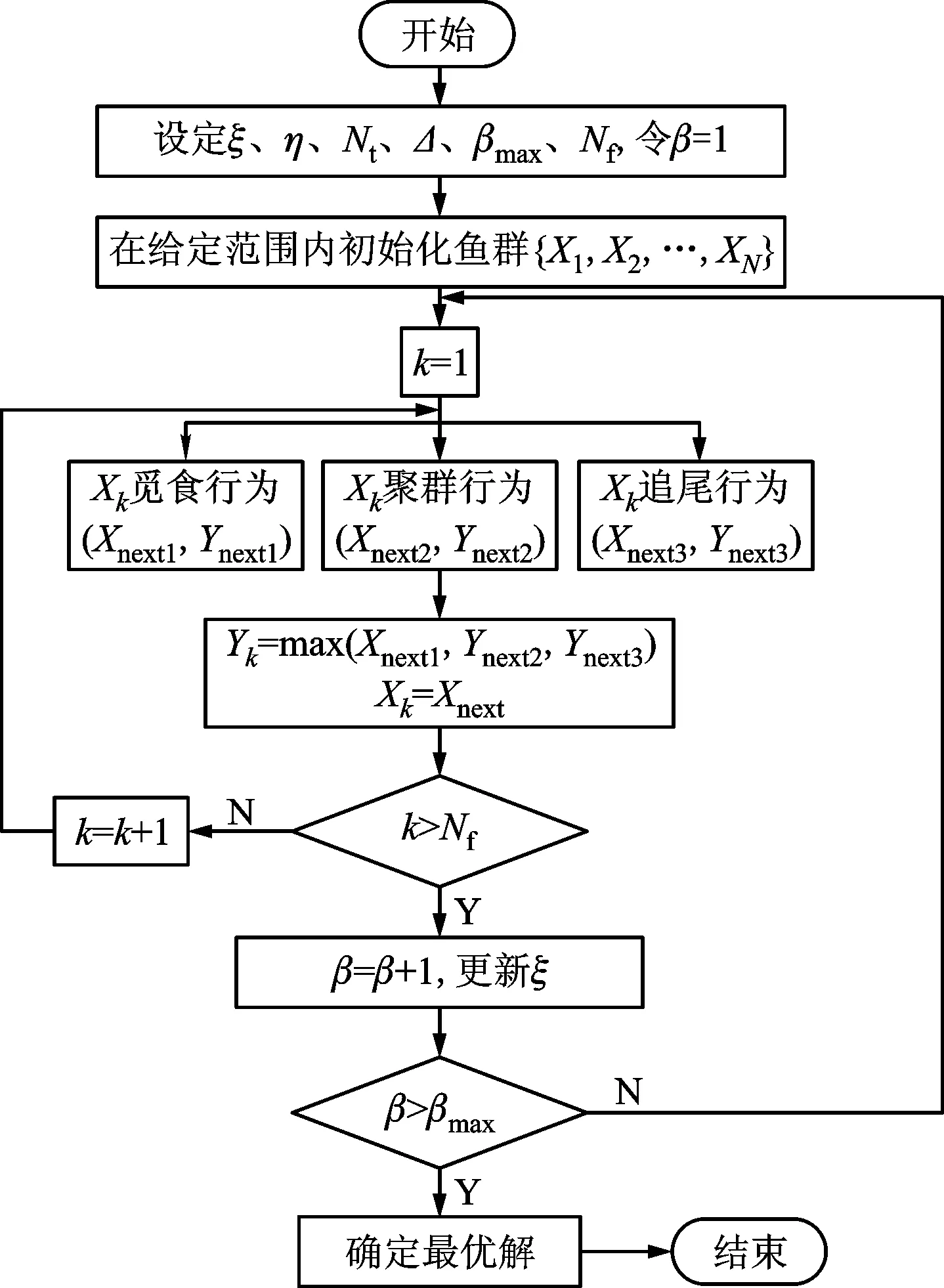
3 仿真与性能评估
3.1 仿真条件

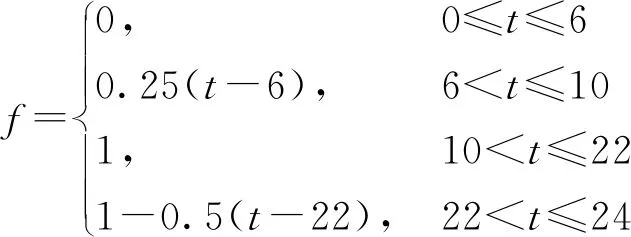
3.2 仿真结果分析





4 结 论
