烟气挡板流动特性的数值模拟
2021-02-22樊桦吴东垠
樊桦,吴东垠
(西安交通大学能源与动力工程学院,710049,西安)
烟气挡板在锅炉运行过程中可以调节烟气流量,对维持和调节锅炉内部负压和再热汽温等都非常重要[1-3]。良好的烟气挡板流动特性可以保证锅炉的安全、经济和稳定运行。在冶金、石化和水泥等行业调整气体流量时均涉及挡板,挡板流动特性与许多工业生产过程密切相关。
流动特性一般可以用速度云图[4-7]、压力云图[8-11]、流阻系数[12-13]和流量系数[14]等描述,近年来常采用CFD方法进行数值模拟。贺惠民等采用Fluent软件比较了某AP 1 000核电汽轮机的中压阀在开度分别为90°、40°和10°下的两相流与单相流的流场,并研究了阀门压损及其主要影响因素[15]。廖志芳等利用CFD方法分析了DN 1 000上盖式半球阀在8个开度下阀门内部流场的变化情况,并根据相关公式得到各开度下的流阻系数和流量系数,进而提供了流阻系数曲线和流量系数曲线,较好地描述了该阀门在不同开度下的流动特性[16]。孙晓等通过数值模拟与实验验证相结合的方法,研究了止回阀的压力云图、速度云图和流阻系数与阀门前后压力差之间的关系,并进行阀芯结构的优化设计[17]。邓斌等基于各向异性多孔介质与分布阻力的概念,采用修正k-ε模型和壁面函数法,计算了管壳式换热器壳侧的流动特性,得到了壳侧在不同雷诺数下的进出口压差和压力分布,将计算结果与实验数据对比,发现计算值和实验值在流量较小时吻合良好[18]。Wang等采用数值模拟的方法研究了柴油发动机燃料引射器的控制阀结构参数对阀内流动特性的影响[19]。Wu等采用CFD方法研究了压力控制阀的压力云图、速度云图和体积流量等,分析压力控制阀的流动-压力特性,并通过实验验证了理论计算结果[20]。综上所述,使用湍流模拟方法计算阀门等部件的内部介质流场,可以得到相应的压力云图、速度云图、流阻系数和流量系数等。这些关键参数均能够反映流动特性,为相应部件的结构优化及运行工况调整奠定基础。
本文采用CFD方法,利用Fluent软件从速度云图、压力云图、流阻系数和流量系数等方面详细研究某烟气挡板的流动特性,优化挡板运行的开度区间,为烟气挡板的设计、校核与选型提供理论依据。
1 数值模拟方法
1.1 物理模型
图1为某烟气挡板的三维模型图,模型与实物尺寸一致。如图1所示,该挡板的主体部分为3片可动挡板,从上到下依次命名为挡板1、挡板2和挡板3。其中,挡板1和挡板3沿顺时针方向打开,挡板2沿逆时针方向打开,最大旋转角度均为90°。运行过程中,3片挡板的旋转角度一致,即若挡板1和挡板3沿顺时针方向旋转40°,则挡板2沿逆时针方向旋转的角度也是40°,将3片挡板同时打开的角度定义为挡板开度,以θ表示。
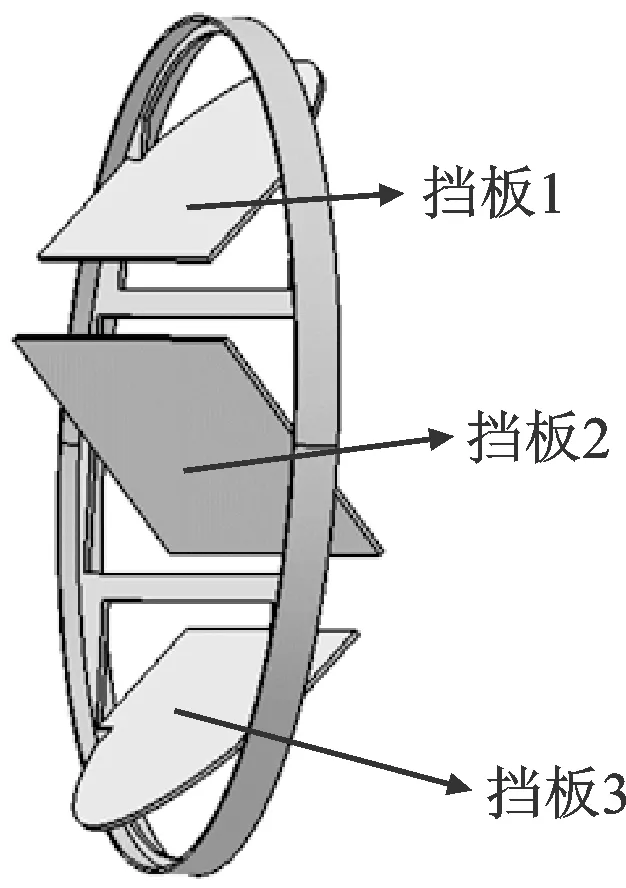
图1 烟气挡板三维模型图
1.2 计算模型及边界条件设置
将烟气挡板安装在圆管烟道内,取烟道一半为计算对象,设置横截面为对称边界,其余边界均设为固体边界。烟气温度为350 ℃并且不可压缩,则其密度和动力黏度分别为0.571 kg/m3和2.995×10-5Pa·s。计算过程中,设置入口速度为18 m/s,出口压力为0 Pa。本文分别模拟了θ为10°、20°、30°、40°、50°、60°、70°、80°和90°时烟道的速度云图、压力云图、流阻系数和流量系数。假定流动为定常流动,利用RNGk-ε双方程湍流模型计算流场,并采用增强壁面函数修正。

图2 θ=40°的网格划分
1.3 网格划分与无关性验证
为了减少计算量,本文取烟道的一半作为计算区域,并利用ICEM划分计算区域的网格。由于挡板结构比较复杂,因此采用非结构网格划分计算区域。图2所示为θ=40°时80万网格的划分情况。由于θ=10°时的网格质量最差,故采用θ=10°的网格进行网格无关性验证。将网格数划分为18万、24万、34万、50万、80万和138万,分别计算挡板前后压降,计算结果如图3所示。从图3中可以看出:当网格数介于18万~50万时,压降随着网格数的增加出现明显波动,这是非结构网格在网格数目较少时网格质量差所致。网格数为80万的计算结果和网格数为138万的计算结果相差不大且无明显波动,说明当网格数为80万时,继续增大网格数目对计算结果影响不大。因此,为了保证计算精度同时节省计算资源,本文选择80万网格数进行数值模拟。
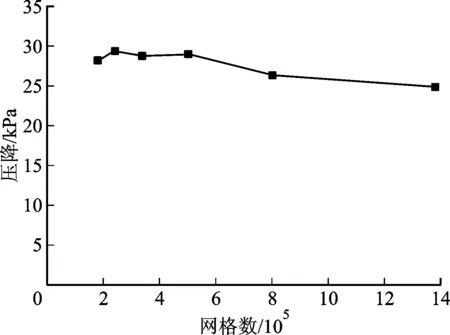
图3 网格无关性验证
2 计算结果与分析
2.1 不同开度对应的烟气挡板速度云图
图4所示为不同θ对应的烟道中间截面的速度云图,本文分别计算了θ为10°、20°、30°、40°、50°、60°、70°、80°和90°时的速度云图,限于篇幅,图4中仅列出有代表性的θ为10°、40°、80°和90°时的速度云图。

(a)θ=10°
从图4a可以看出:当θ=10°时,挡板下游开口附近的烟气速度明显高于其他区域的烟气速度,且挡板2和挡板3之间的烟气流速明显大于挡板1和挡板2之间的烟气流速。这是因为挡板1和挡板2之间形成了扩散结构,烟气在挡板1和挡板2的上游开口处由于流通截面积较小,烟气速度较大,因此烟气流经扩散结构向下游动时,随着流通截面积增大,速度会相应下降;与此对应,由于挡板2和挡板3之间形成收缩结构,烟气在挡板2和挡板3的上游开口处速度较低,向下游流经收缩结构时速度明显上升,在挡板2和挡板3的下游开口处形成明显的高速区。如图4b和图4c所示,随着挡板开度的增大,烟道内高速区域增多,烟道上半部分的高速区域始终多于烟道下半部分,θ为20°、30°、50°、60°和70°时,速度云图的变化规律与上述一致,在此不再赘述。当θ增大到80°时,从图4c中可以看出,烟道上半部分和下半部分的高速区域面积相近;若θ增大到90°,如图4d所示,烟道上半部分和下半部分的高速区域面积几乎完全相等,整个烟道内速度场的均匀性最好。
从图4还可以看出,若θ=10°,整个烟道内烟气的最大流速约为235 m/s,与烟气入口速度18 m/s相差极大,说明θ=10°的烟道内部速度场分布极不均匀。但是,随着θ的增大,烟气的最大速度快速降低,当θ=40°时,烟气的最大流速下降到约92.9 m/s,烟道内部速度场分布的均匀程度有了很大的提升。若θ继续增大,烟气的最大速度持续下降,但是下降的趋势变缓,θ为20°、30°、50°、60°和70°时,烟气最大流速的变化趋势与上述情况吻合。当θ=90°时,烟气的最大速度降低到约31 m/s,与烟道入口速度18 m/s相差不大,烟道内速度场分布基本均匀。
2.2 不同开度对应的烟气挡板压力云图

(a)θ=10°
图5为不同θ对应的烟道中间截面压力云图,本文分别计算了θ为10°、20°、30°、40°、50°、60°、70°、80°和90°时的压力云图,限于篇幅,下文仅列出θ分别为10°、40°、80°和90°时的速度云图。当θ=10°时,从图5a可以看出,挡板上游静压明显大于挡板下游静压,压力过渡区域面积非常小,烟气压力在挡板开口附近急剧下降。随着θ的增大,挡板开口附近的压力过渡区域的面积逐渐变大,挡板上、下游的压力差也变得越来越小,压力场分布的均匀化程度提高,θ为20°、30°、50°、60°和70°时,压力云图的变化规律与上述一致。当θ=80°时,由图5c可知,挡板上、下游的压力相差不大,但在挡板上游开口附近仍然有局部高压区域出现,压力场整体分布较为均匀;当θ增大到90°时,由图5d所示,挡板上、下游的压力非常接近,挡板附近几乎没有明显的高压区域出现,此时压力场分布相对于其他开度是最均匀的。
从图5还可以看出:当θ=10°时,整个烟道内烟气的最大静压约为26.50 kPa,而最小静压约为-11.40 kPa,两者之间相差37.90 kPa,说明烟道挡板附近的压力场分布极不均匀。随着挡板开度的增大,烟气的最大静压迅速下降,最小静压迅速增大,二者之间的差值快速减小。当θ=40°时,烟道内的烟气最大静压约为1.58 kPa,最小静压约为-1.44 kPa,两者之间相差3.02 kPa,其压力场与θ=10°的情况相比其均匀化程度大幅度提高。若θ继续增大,烟气的最大静压下降和最小静压上升的速度明显减缓,θ为20°、30°、50°、60°和70°时,烟气静压的变化规律与上述类似。若θ=90°,烟气的最大静压约为0.13 kPa,最小静压约为-0.22 kPa,两者之间相差仅为0.35 kPa,此时的烟气压力场分布非常均匀。
2.3 不同开度对应的烟气挡板流阻系数
流阻系数是评价节流元件流动特性的一项重要指标,表征流体通过节流元件时产生的压力损失的大小,其计算公式[21]如下
ξ=2Δp/(ρu2)
(1)
式中:ξ为流阻系数;Δp为挡板前后压差,Pa;ρ为烟气密度,kg/m3;u为烟气速度,m/s。
根据数值模拟结果计算得到不同挡板开度对应的流阻系数,如图6所示。

图6 不同挡板开度对应的流阻系数
如图6所示,ξ与θ基本呈反比例关系:当θ较小时,ξ随着θ的增大迅速下降,θ=10°对应的ξ为285.28,而θ=40°对应的ξ为16.02,相比θ=10°而言下降了94.38%;当θ较大时,ξ随着θ的增大而下降的趋势变缓,当θ=50°时,对应的ξ为7.47,相比θ=10°时下降了97.38%,而θ增大到90°时,ξ为0.58,较θ=10°时下降了99.80%,说明该挡板在小开度下流动阻力很大。为了降低挡板的阻力,保证设备的经济运行,挡板的开度宜大于40°。
某电厂要求烟气挡板在烟气流速18 m/s下全开的阻力不超过100 Pa,根据式(1)换算成对应流阻系数,可得ξ为1.08,而数值模拟结果显示θ=90°对应的阻力仅为54 Pa,流阻系数为0.58,可见,该挡板特性满足工程实际的要求。
2.4 不同开度对应的烟气挡板流量系数
流量系数表征流体在一定阻力下通过节流元件的流量,也可以用来评价流动特性,其计算公式[21]如下
(2)
式中:Cv为流量系数;Qv为烟气流量,m3/h。
结合数值模拟结果和式(2)求得挡板的流量系数Cv,如图7所示。

图7 不同挡板开度对应的流量系数
从图7可知:Cv随θ的增大而增大。当θ≤10°时,Cv随θ的增大而增长的趋势较为缓慢;当θ=10°时,Cv为532.69;当θ=49°时,Cv为2 247.81,与θ=10°时相比增大了321.97%;当θ>10°后,Cv随θ的增大而增加的趋势较为迅速,θ=50°对应的Cv为3 291.89,比θ=10°时增大了517.97%,而θ=80°对应的Cv为10 059.31,较θ=10°时增大了1 788.40%。但是,当θ从80°增大为90°时,Cv随着θ的增大而增加的速度略有下降,说明挡板在θ介于80°~90°之间的流量调节能力较弱,当θ=90°时,Cv最大,为11 775.72。
2.5 引风机全压恒定时的烟气质量流量特性
在实际应用过程中,由于烟道内烟气的流动与相关引风机密切相关,了解挡板在引风机全压恒定时的开度θ与烟气质量流量Q之间的关系非常重要。本文根据某电厂实际运行需求,计算了当余热利用装置的引风机全压为1 000 Pa时,烟气质量流量Q与θ之间的关系。
当引风机全压为100 Pa,即引风机入口压力为-1 000 Pa时,假设从0压点到引风机入口的烟道尺寸不发生改变,则烟气速度不发生变化。根据伯努利方程,从0压点到引风机入口处有
(3)
式中:ξ0为其他阻力系数,表示压点和引风机之间挡板以外的其他所有阻力损失之和的阻力系数,在本文范围内为常数。在上文数值模拟计算结果中,当θ=90°、u=18 m/s时,ξ=0.58的工况比较符合某电厂的实际运行需求,由此可得ξ0=10.23。将ξ0和ξ代入式(3),可以得到在引风机全压为1 000 Pa下不同挡板开度θ对应的烟气流速u,进而得到烟气质量流量Q如图8所示。
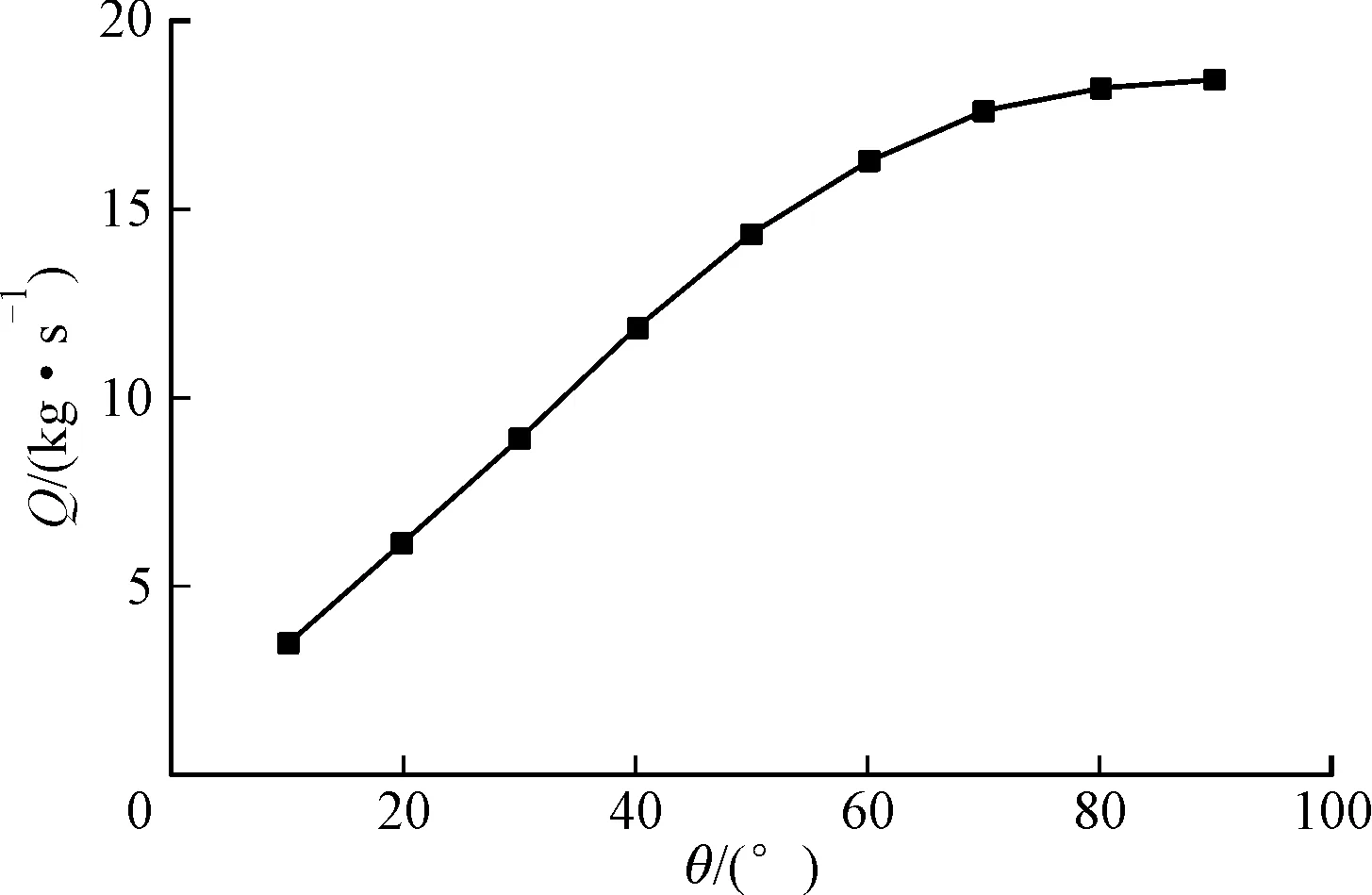
图8 引风机全压为1 000 Pa时挡板的质量流量
从图8可以看出:当引风机全压为1 000 Pa时,Q随着θ的增大而增长;当1°≤θ≤60°时,Q随θ的增大而增大的趋势近似为线性,当θ=10°时,Q为3.52 kg/s,当θ=60°时,Q为16.28 kg/s;若θ>60°,Q随着θ的增大而增大的趋势逐渐变慢,当θ=70°时,Q为17.62 kg/s,当θ=80°时,Q为18.22 kg/s,而θ=90°时,Q最大,为18.4 kg/s。
根据某电厂锅炉的运行需要,要求θ每变化10°,烟气质量流量变化5%左右。为了优化挡板的开度区间,假设相邻两个计算开度之间的流量分布近似为线性,则可以得到引风机全压为1 000 Pa时的烟气质量流量与挡板开度之间的分段函数

(4)
由式(4)可以计算挡板开度θ与烟气质量流量Q之间的对应关系。当θ=i时,对应的烟气流量增长率qi的计算公式为
(5)
式中:Qi为θ=i时对应的烟气质量流量,kg/s;Qi-1为θ=i-1时对应的烟气质量流量,kg/s。
由式(5)计算可知:当θ≥17°时,θ每增大1°,流量增长率q近似等于或小于5%,说明挡板的流动调节能力较好;然而,在θ>80°后,θ每增大1°,流量增长率q仅为0.1%,说明此时挡板几乎不具备调节流量的能力。因此,在挡板的实际工作过程中应尽量使常用开度避开0°~16°和81°~89°的区间,尽可能在开度17°~80°之间调节烟气的质量流量。
综合考虑前文计算得到的挡板的流阻系数特性和流量系数特性,建议该挡板的常用工作开度区间为40°~80°。
3 结 论
本文采用数值模拟方法,计算了烟气速度为18 m/s时的烟气挡板在9个开度下的速度云图、压力云图、流阻系数和流量系数,分析了该挡板的流动特性,并结合某电厂锅炉的实际运行情况,研究了该挡板在引风机全压1 000 Pa下的质量流量特性,确定了该挡板的优化开度区间。
(1)对于速度云图,当θ较小时,高速区主要集中在挡板开口处,并且烟道下游的高速区域的面积明显大于上游;随着θ的增大,烟道中高速区域变大,速度场均匀化程度变好,烟气最大速度下降;当θ=90°时,烟道内速度场分布基本均匀。对于压力云图,当θ较小时,挡板前后压力相差很大;随着θ的增大,挡板前后压力差变小,压力场分布均匀性变好;当θ=90°时,挡板前后压力非常接近,压力场分布基本均匀。
(2)挡板流阻系数ξ与挡板开度θ大致呈反比例关系。当θ较小时,ξ随θ的增大而减小的速度很快。若θ较大,ξ随θ的增大而减小的趋势趋于平缓。因此,建议挡板常用工作开度应大于40°。在烟气速度为18 m/s的条件下,某电厂要求挡板全开阻力不得超过100 Pa,对应挡板流阻系数ξ为1.08,模拟计算得到θ=90°对应的ξ为0.58,满足电厂实际运行的需求。
(3)挡板流量系数Cv随着挡板开度θ的增大而增大,当θ较小时,其速度较慢;当θ较大时,其速度较快,而θ从80°增大为90°时,其速度略有下降。
(4)当余热利用装置的引风机全压为1 000 Pa时,若θ≥17°,θ每增大1°对应的流量增长率q近似等于小于5%,挡板的流动调节能力较好。而θ>80°后,θ每增大1°对应的流量增长率q仅为0.1%,挡板流动调节能力很差。因此,该挡板的流动调节适用开度范围为17°~80°。
(5)综合考虑挡板流阻系数特性和流量调节特性,建议该挡板的常用工作开度介于40°~80°之间。
