基于深度学习视角对初中数学一次函数教学的几点思考

齐立华

【摘要】基于深度学习的视角，课堂教学中要避免“零”“散”现象，要关注知识的系统性和前后的关联性，注重从知识的本质出发展开教学.从数学课程的核心内容角度分析，“一次函数”是一个隶属于“函数”这个大单元的小单元，是函数的起始.教师在教学中要注重让学生整体感知函数的学习方法，将数学关键能力和学科素养的培养渗透到教学环节.

【关键词】单元;深度学习;整体性

一、深度学习视角下的“单元”

深度学习的概念由美国学者于1976年提出，国内学者也对此进行了大量研究.深度学习强调学生应具有主动学习、批判学习、终身学习、创新学习等学习特征，它是一种有意义的学习方式，有助于培养学生的思维品质.学生的深度学习必然是在教师的深度教学下发生的.深度学习并不是指教学内容上的深度，而应该是指向学生思维和情感的深度发展，实现课堂教学的核心价值——培养学生终身发展的必备品格与关键能力.深度学习是学生主动参与学习、实现自主构建的过程，并通过教师适当的指导提高学生成功的体验感、自我效能感.教师在学生自主学习的过程中予以指导，除了要关注学科知识外，更要关注学习过程的开展、思想方法的渗透，将学科关键能力和核心素养的培养在教学过程中落实.[1]

“单元”是在一个大的整体中自成系统、段落的小整体.在深度学习的视角下，“单元”即从整体的视角看待课程内容，包括大单元、中单元、小单元以及微单元.深度学习视角下的“单元”并不等同于教材编排以章节形式呈现的教材单元，它基于教材单元，又对不同教材单元实行统筹.鉴于数学学习内容的特点和学生认知水平发展的特征，以螺旋上升的方式编排教材是在教材编排中经常采用的方式.因此，大单元下的小单元会分布在不同的教材单元中，这样隶属于同一个大单元的不同小单元将被安排在不同的教材单元，而这些教材单元之间必然存在着某种思想、方法以及逻辑上的联系.我们只有站在整体的角度看待这些分布在不同教材单元中的小单元，才可以从整体的角度把握知识，有利于学生有效迁移的发生，使学生更好地掌握知识，提升学科素养和关键能力.

二、再探一次函数教学

函数是初中阶段乃至高中阶段的核心知识.初中阶段学习的函数的概念、一次函数、反比例函数以及二次函数，是学生后续学习三角函数、指数函数等复杂函数的基础.随着学习的深入，虽然研究的对象逐渐复杂，但研究函数的方法却是一脉相承的：基于实际问题得到函数表达式;基于函数表达式，通过三步画出相应的函数图像（列表，描点，连线）;基于函数图像探究其相关性质以及与相应方程、不等式之间的关系.“一次函数”是“函数”这个大单元的起始单元，教师在教学中要基于“一次函数”这个小单元，着眼于“函数”这个大单元，注重渗透研究函数的方法，让学生通过学习这个小单元，整体感知“函数”大单元的研究方法.本文从深度学习的视角谈了对函数、一次函数的概念和一次函数图像教学的几点思考.

1.对函数教学的思考

苏科版教材八年级上册6.1函数，从整体的角度来看，本节内容是“函数”这个大单元下的一个小单元，是学生认识函数的起点，是学生的学习从定量到变量的飞跃，对学生后续学习函数有至关重要的影响.在传统的教学中，一般都是基于实际问题引出函数概念，然后对函数概念进行辨析（辨析在一个表达式中，一个变量是否是另一个变量的函数：如y=x2中，y是否是x的函数，反过来，x是否是y的函数）.

就如波利亚所指出的，如果你太过深入到细节中去，你很有可能在细节中迷失自我，太多的细枝末节只会加重思维负担，它们会分散你的注意力，阻碍你对要点内容投入足够的注意力，甚至使你根本看不到要点.[2]学生往往将重点放在“细节”处，在概念的辨析中“迷失自我”，忽视了通过实际问题引出函数概念这一过程.而从实际问题到函数概念的过程正是培养学生通过建立数学模型解决实际问题这一核心素养的时机.在这一教学过程中，教师应该让学生深刻感知函数是解决实际问题时一种十分有用的模型，并通过有效的课堂练习让学生初步建立利用函数模型解决实际问题的意识.这种意识对于学生后续学习用一次函数解决问题以及用二次函数、反比例函数解决问题都有重要的意义.教师在练习中可以渗透不同类型的函数形式，让学生从整体上认识和把握函数.

2.对一次函数教学的思考

苏科版教材八年级上册6.2一次函数，本节要讲的一次函数是学生在学习了函数的基础上学习的第一种特殊函数.传统教学中采用给汽车加油等实际问题引导学生得到函数表达式，通过分析以上函数表达式的共同特征得到一次函数的一般表达式.

从深度学习的视角考虑，本节课虽然是探索一次函数，但不应仅仅局限于此.在由实际问题得到函数表达式这一板块，可以穿插其他函数形式（如反比例函数、二次函数等），这样可以进一步巩固学生对函数本质的认识，增强学生利用函数模型解决实际问题的意识，也有利于学生从整体上感知“一次函数”是“函数”这个大单元下的一个小单元.

从一个个具体的一次函数表达式中抽象出一次函数表达式的一般形式，是一个从具体到抽象的过程.教师在教学中不仅要注重学生是否掌握了一次函数表达式，是否能正确判断一个函数是否属于一次函数，更应该注重引导学生由一个个具体的表达式抽象出一般表达式，这样才能促进学生深度学习的发生，在关注知识获得的同时，发展学生的学科核心素养和关键能力.[3]

3.对一次函数的图像教学的思考

苏科版教材八年级上册6.3一次函数的图像，在本节中学生将首次接触到函数图像的概念.因此，一次函数图像的教学不能仅仅停留在一次函数的图像上，教师要站在函数图像的高度，在一次函数图像的教学中让学生充分感知由函数表达式得到函数图像这一过程：①通过列表表示自变量与函数值;②在坐标系中描点;③用光滑的曲线将这些点顺次连接起来，得到函数图像.

在一次函数图像的教学中，教师可以让学生独立完成①②两个步骤，在步骤③中让学生充分思考：应如何连接坐标系中所描出的那些独立的点呢？在教学中，教师可充分借助信息技术手段，让学生直观感知：不断在两个独立的点之间增加点，这些点最终将连成一条线，而这条线就是我们得到的函数图像（对一次函数而言，这些点最终形成的是一条直线）.如果教师在第三步急于求成，只站在一次函数图像的角度，让学生直接用直線（或线段）连接坐标系中描出的点，进而得到其图像，那么容易给学生造成误解，认为只要用直线将描出的点连接起来就可以得到函数图像，这对于学生后续学习二次函数、反比例函数的函数图像是十分不利的.

此外，在一次函数图像的教学中，教师不能急于向学生传授其简便画法，即通过两个点便可确定一次函数的图像.一次函数图像的简便画法应该是学生在不断地进行列表、描点、连线的过程中自己总结和发现的，如果急于告知学生简便画法，容易让学生误认为画函数图像只需要找到两个点即可，这样当学生遇到一个新的函数时，可能会无法正确画出其函数图像.

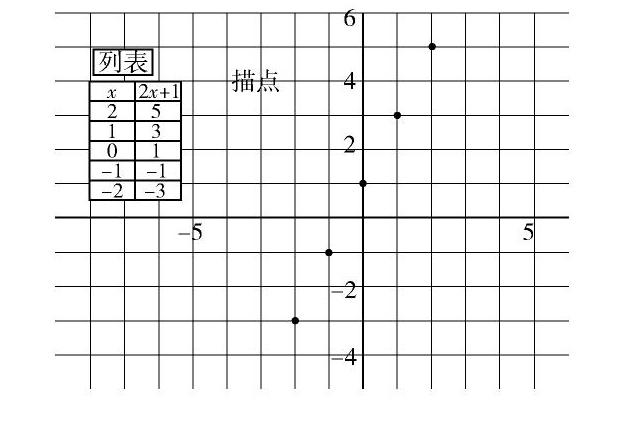
【教学案例】绘制y=2x+1的函数图像.

利用几何画板，完成对函数y=2x+1列表、描点的步骤，在连线这一步骤，借助几何画板追踪点的轨迹的功能，不断增加图像上的点，如下图所示.在这一过程中，教师让学生感知函数图像是由无数个在函数图像上的点所组成的，并直观感受一次函数的图像上所有的点最终能连成一条直线.

结 语

本文基于深度学习的视角，阐述了站在“函数”这个大单元，进行“一次函数”这个小单元教学的几点思考.函数是学生在学习中由定量到变量质的飞跃.教师在函数的教学中，要让学生充分感知利用函数模型解决实际问题中含有两个变量的问题这一过程，在这一过程中帮助学生建立利用函数模型解决实际问题的意识，培养学生“数学建模”这一核心素养.在一次函数的教学中，教师应基于一个个具体的一次函数表达式，引导学生进行深度思考，充分激发学生的符号意识，实现从具体到抽象的过渡，这正是数学学科素养中数学抽象的能力.在一次函数图像的教学中，教师要让学生思考坐标系中独立的点如何构成完整的函数图像，让学生感知函数图像是在不断增加所取点的过程中形成的一条连续的线，培养学生数形结合的意识，使其最终认识到函数图像可通过用光滑曲线连接坐标系中的相邻点得到.

在教学过程中，教師不仅要关注学生对知识的掌握与学习，更要注重学生对学习的过程的理解与生成.在后续的函数学习中，虽然函数的形式会发生变化，但研究函数的方法却是始终如一的，所以在教学中，教师要注重学生对探究函数的过程、方法的掌握，这样有利于学生在学习后续函数时进行有效的迁移.[4]所以，在进行“一次函数”这个小单元的教学时，教师要从“函数”这个大单元出发，进行整体性教学，注重学生核心素养和关键能力的培养.

【参考文献】

[1]刘月霞，郭华，刘晓玫.深度学习：走向核心素养（学科教学指南·初中数学）[M].北京：教育科学出版社，2018.

[2]波利亚.怎样解题：数学思维的新方法[M].涂泓，冯承天，译.上海：上海科技教育出版社，2007.

[3]王久成，郭恒武.基于SOLO分类的深度学习研究：以“函数”教学为例[J].数学学习与研究，2020（11）：24-26.

[4]陈丽芳.浅谈深度学习理论下初中数学课堂教学模式[J].新课程导学，2020（11）：91.