基于SO(3)空间的线性自抗扰姿态控制方法
2021-02-18黄吉传缪存孝
黄吉传,张 贺,缪存孝
(1.航空工业成都飞机工业(集团)公司,成都 610092;2.西北工业大学电子信息学院,西安 710129;3.空军装备部驻成都地区第一军事代表室,成都 610092;4.北京科技大学机械工程学院,北京 100083)
0 引言
因具有垂直起降、悬停和自主飞行等功能,四旋翼飞行器被广泛应用于军事和民用等领域,逐渐成为学术研究中的一个热点[1]。在军事应用上,无人飞行器可以作为侦察机或战斗机,执行战场侦察、通信中继、目标定位、定点精确轰炸、拦截导弹等重要军事任务[2]。在民用方面,无人飞行器被用于灾区搜救、航空拍摄、气象探测、电力线路巡查等高空复杂任务[3⁃4]。 然而,四旋翼飞行器是一个典型的多变量、非线性、强耦合的欠驱动系统,其控制器设计十分困难。近年来,研究人员针对四旋翼飞行器的建模、控制及工程应用开展了大量研究工作[5⁃10]。目前,四旋翼飞行器的飞行控制系统设计及工程应用是一个主要的研究方向。四旋翼飞行器的飞行控制系统一般采用内外双环控制,内环为姿态控制环,外环为位置控制环,在一些实际应用中,位置控制可使用远程遥控,而姿态控制通常都由机载系统自主完成,机体位置的变化也是由姿态变化引起的,因此姿态控制是整个飞行控制系统的基础和关键[11⁃12]。四旋翼飞行器在实际飞行中易受外部干扰,因此设计鲁棒性强、抗干扰性好的四旋翼飞行器姿态控制系统是关键。
四旋翼飞行器的控制策略目前分为三大类,包括:1)最为常见的PID控制、线性二次型等局部线性控制[13⁃14];2)反步法、 滑模控制、 自适应控制等非线性控制[15⁃16];3)神经网络控制、 模糊控制等智能控制[17⁃18]。以上方法或对非线性考虑不足,与实际系统相差较远,导致实际飞行中控制效果不理想;或对模型精确度要求较高,在实际应用中的控制效果还有待提高;或是算法较为复杂,难以实现。同时,以上方法的姿态大多采用Euler角及方向余弦矩阵进行表示,以此为基础建立的姿态系统模型是局部的、不完备的,甚至有可能出现计算奇异性,使得需要在奇异点进行特殊处理,从而增加了控制器设计的难度。近年来,几何控制的方法[19⁃24]逐渐应用于四旋翼飞行器控制中,并取得了良好的控制效果。它通过将四旋翼的姿态向量映射到特殊正交群SO(3)空间,极大简化了四旋翼的模型表示方法,并优化了控制器的设计过程。国外学者Lee等[19⁃21]在这方面做了大量的深入研究,先后采用非线性PID、鲁棒自适应等控制方法设计控制器,取得了丰硕的理论成果。国内目前对基于SO(3)的姿态控制研究相对较少,刘锦涛等[22⁃23]从理论上研究了四旋翼 SO(3)滑模变结构控制、自适应控制,并进行了仿真实验,但均未进行实际的实验验证。 刘超等[24]在SO(3)上设计了滑模观测器并应用于四旋翼平台上对实际姿态和旋转角度进行观测,验证了观测器的效果。针对四旋翼飞行器非线性、强耦合、易受外部干扰的特性,自抗扰控制[25⁃26](ADRC)越来越多地应用于四旋翼飞行器控制中,但是基于ADRC的控制器采用非线性函数,参数较多、调节复杂,在实际应用中难以简单快速实现。故本文提出了一种基于SO(3)空间的线性自抗扰姿态控制(LADRC)方法,通过室内姿态控制实验和室内悬停实验证明了该方法可以提高四旋翼飞行器姿态控制系统的抗干扰能力。
1 SO(3)四旋翼飞行器数学模型
在刚体的三维空间运动中,惯性系与刚体本体坐标系之间的转换矩阵可以用一个正交变换矩阵R来描述,所有的正交变换矩阵构成特殊的正交矩阵群:
四旋翼飞行器的姿态运动方程可表示为[19⁃21]
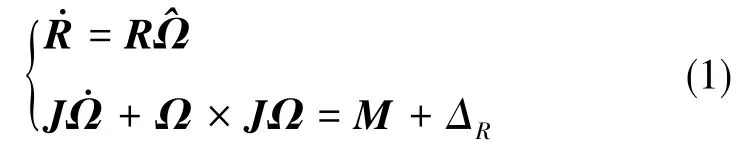
式(1)中,R∈SO(3)为飞行器本体坐标系到惯性坐标系的旋转矩阵;Ω∈R3为机体角速度;^Ω为Ω的hat映射;J∈R3×3为机体坐标系下的惯性矩;M∈R3为控制力矩;ΔR∈R3为姿态动力学中的未知外部干扰,且为正常数。
设x=[x1x2x3]T, 定 义运 算为hat映射,记为∧。 hat映射的逆运算为vee映射,记为∨, 定义为将任意三 维 反 对 称 阵 映 射 为 三 维 向 量[19⁃21], 即
2 基于LADRC的姿态控制器设计
针对四旋翼飞行器非线性、多变量、强耦合和对扰动敏感等控制问题,设计了基于线性扩张状 态 观 测 器 (LinearExpansion StateObserver,LESO)的姿态控制系统,如图1所示。图1中,R为目标旋转矩阵,u0为PD控制输出,b0为补偿因子,zi(i=1,2,3)为观测值,u为控制器输出,y为系统输出。

图1 姿态控制系统结构Fig.1 Structure of attitude control system
2.1 线性扩张状态观测器(LESO)设计
将力矩矢量M∈R3看作四旋翼飞行器系统的控制输入量,则式(1)可以改写为
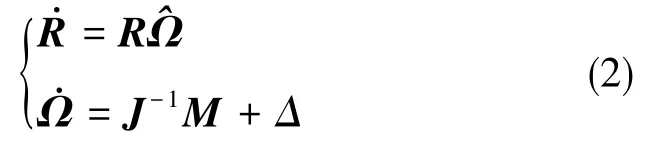
进一步可写为
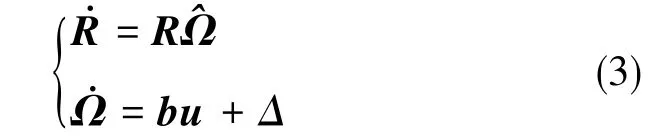
式(3)中,b为等效输入矩阵,与机体参数相关。
根据文献[19]~文献[21],定义估计的机体坐标系到惯性坐标系的转换矩阵Rz与机体坐标系到惯性坐标系的转换矩阵R的误差为

设计离散递推式的线性扩张状态观测器(LESO)为
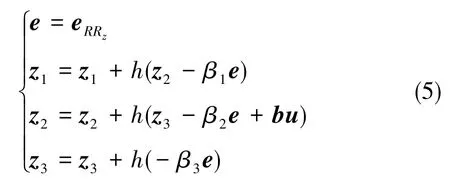
式(5)中,zi(i=1,2,3)为观测值;h为采样周期;βi(i=1,2,3)为观测值增益,并且β1=为观测器带宽。
2.2 线性反馈控制律(LSEF)设计
四旋翼飞行器的姿态控制采用内外双环控制,外环为位置控制产生的姿态角设定值,输出的是角速度设定值,而内环则根据输入的角速度设定值进行控制。基于LADRC的姿态控制器结构如图2所示[27],由于LESO能够实时估计并补偿内部与外部扰动,因此传统PID中在常值扰动下为消除静差而采用的积分器已不再必要,线性状态误差反馈控制率进一步简化为PD组合的设计。

图2 基于LADRC的姿态控制器Fig.2 Attitude controller based on LADRC
估计的机体坐标系到惯性坐标系的转换矩阵Rz与期望的机体坐标系到惯性坐标系的转换矩阵Rd的误差为

式(6)中,Rz=z1。
角度环采用比例控制,控制率为

角速度环线性反馈控制率为
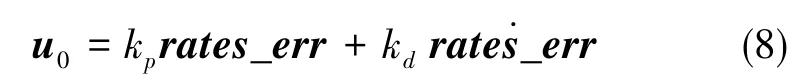
式 (8)中, 角 速 度 误 差 为rates_err=rates_sp⁃z2,kp、kd分别为比例(P)和微分(D)的放大系数。
则扰动补偿过程为

3 实验验证及结果分析
对所设计的控制方法在实际四旋翼飞行平台中进行实验验证,室内飞行平台由四部分组成:地面站、通信系统、四旋翼飞行器以及Optitrack室内光学定位系统,实验平台结构如图3所示,其实验环境如图4所示。基于Simulink编写地面站,通过Motive定位解算软件获取四旋翼飞行器的位置和姿态数据,采用Mavlink通信协议编写串口通信模块,通过Wifi实现地面站与飞控间的通信,机载控制板采用开源飞行控制器Pixhawk,四旋翼机架为轴距280mm的碳纤维机架,质量小且强度高。

图3 实验平台结构Fig.3 Structure of experiment platform

图4 实验环境Fig.4 Schematic diagram of experiment environment
3.1 姿态控制实验
本文研究的重点是对飞行器姿态的控制,通过辅助的四旋翼固定架将飞行器的位置运动自由度锁定。如图5所示,四旋翼飞行器固定于带有3⁃DOF旋转关节(万向节)的基座上,从而使得飞行器只有3个姿态运动的自由度。

图5 姿态控制测试平台Fig.5 Experiment platform of attitude control
由于实验中采用Optitrack室内光学定位系统可以获得四旋翼的高精度位姿信息,所以实际控制中角度误差计算采用
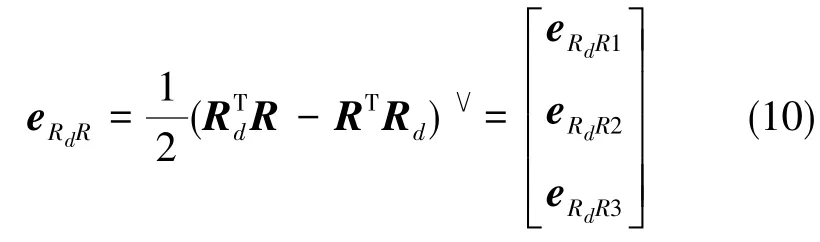
角速度误差计算采用
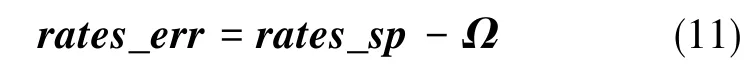
分别进行3种情形下的实验验证:
实验一:期望姿态角均为0°时,施加干扰力矩,并与PID控制方法进行对比。
实验二:期望姿态角为正弦信号时,不施加干扰,并与PID控制方法进行对比。
实验三:期望姿态角为正弦信号时,施加干扰力矩,并与PID控制方法进行对比。
(1)实验一
实验一中设定的期望姿态为θ=0°、φ=0°,稳定飞行过程中在俯仰和横滚方向突然施加干扰力矩(以挂载200g砝码实现),PID控制与本文算法的实验结果分别如图6和图7所示。可以看出,PID控制在静态条件下θ的稳态偏差为0.98°左右,φ的稳态偏差为1.23°左右,受到外界干扰后姿态角出现了10°左右的偏差;本文算法在静态条件下θ的稳态偏差为0.50°左右,φ的稳态偏差为0.33°左右,受到外界干扰后姿态角出现4°左右的偏差。

图6 静态抗干扰下的俯仰角曲线Fig.6 Curves of pitch angle under static anti⁃interference

图7 静态抗干扰下的横滚角曲线Fig.7 Curves of roll angle under static anti⁃interference
可见,静态条件下本文设计的基于干扰观测器的姿态控制器比PID控制更稳定,同时在系统遭遇扰动时,干扰造成的输出波动幅值变化更小,平均降低约50%,表现出了更强的抗干扰能力,说明系统具有较好的自适应性。
(2)实验二

图8 动态跟踪下的俯仰角曲线Fig.8 Curves of pitch angle under dynamic tracking

图9 动态跟踪下的横滚角曲线Fig.9 Curves of roll angle under dynamic tracking
(3)实验三
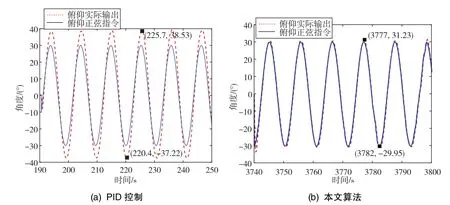
图10 动态抗干扰下的俯仰角曲线Fig.10 Curves of pitch angle under dynamic anti⁃interference

图11 动态抗干扰下的横滚角曲线Fig.11 Curves of roll angle under dynamic anti⁃interference
3.2 悬停实验
悬停实验采用Optitrack室内光学定位系统获得机体的空间位置,位置控制方法采用串联PID控制,位置环采用P控制,速度环采用PID控制,姿态控制方法采用上述线性自抗扰控制,期望位姿设置为:(0m,0m,-1m,0°), 高度方向的跟踪曲线如图12所示。

图12 悬停实验高度跟踪曲线Fig.12 Height tracking curve in hover experiment
由图12可知,悬停时高度误差小于3cm,间接验证了本文提出的线性自抗扰姿态控制方法的有效性。
4 结论
本文提出了一种基于SO(3)空间的线性自抗扰姿态控制(LADRC)方法,可得如下结论:
1)静态条件下,θ和φ的稳态偏差小于1°,受到外界干扰后姿态角可以5s内迅速恢复;
2)动态条件下,θ和φ可以精确快速跟踪设定值,当存在外界干扰时,θ和φ仍然可以快速跟踪设定值,在幅值处出现1°左右的跟踪误差;
3)悬停时采用本文提出的姿态控制方法,悬停精度优于3cm;
4)实验表明,在静动态条件下,本文所提出的姿态控制器可提高姿态跟踪的鲁棒性,有很强的抗干扰能力,能够满足四旋翼无人机的姿态控制要求,具有实际应用价值。
