INS/CNS/GNSS机载高性能空中对准技术研究
2021-02-18陈善秋武庆雅吴禹彤张丽玲夏宇强龙腾宇
陈善秋,武庆雅,吴禹彤,张丽玲,夏宇强,龙腾宇
(1.国防科技大学空天科学学院,长沙 410073;2.北京航天时代激光导航技术有限责任公司,北京 100094)
0 引言
捷联惯导系统(Strapdown Inertial Navigation Sys⁃tem,SINS)在进入正常导航工作状态之前必须进行初始对准。初始对准为SINS工作提供初始姿态航向信息,是影响导航系统性能的关键技术之一,在很大程度上决定了惯导系统的工作精度和快速反应能力[1]。一般情况下,载机可以在地面完成静基座初始对准,但紧急情况下载机可能要随时起飞,需要在空中通过动基座对准方式完成初始对准。
载机在空中一般通过卫星导航系统(Global Navigation Satellite System,GNSS)提供的速度和位置信息进行对准[2],但实际应用中该方法对准时间长,精度也无法得到保证。近年来,学者们提出了一些新的机载动基座初始对准方法,如利用视觉、 Doppler测速、 雷达等辅助的方法[3⁃6]。 随着星敏感器探测能力的提升,大气层内全天时小视场星敏感器日益成熟,长航时远程飞机开始配备天文导航设备[7]。 天文导航系统(Celestial Navigation System,CNS)定向精度是目前所有导航系统中最高的,且定位精度次于GNSS。为充分发挥GNSS与CNS各自的优势,本文提出了一种基于卫星天文辅助的机载惯导空中对准方法。由于GNSS与CNS的输出频率不同,且不一定具有整数倍数关系,若使用集中滤波、联邦滤波或传统意义上的序贯滤波,则需要对量测信息进行内插外推,不仅计算量大,还会造成一定程度的精度损失。针对此问题,本文采用广义序贯滤波方法来实现多传感器的异步信息融合。仿真结果表明,该方法能够提升机载惯导空中对准精度,同时缩短对准时间,在很大程度上提升了武器装备的精确打击能力和快速反应能力,可支持飞机应急起飞等突发性作战要求,使其在作战中处于主动地位,具有一定的工程应用价值。
1 卫星天文辅助空中对准模型建立
1.1 坐标系定义
地心惯性坐标系(i系):地心惯性坐标系不随地球自转,其坐标原点为地心,OXi轴、OYi轴在地球赤道平面内,OXi轴指向春分点,OZi轴指向地球极轴,由右手定则决定OYi轴方向。
地球坐标系(e系):地球坐标系是固连在地球上的坐标系,随地球旋转,其原点为地球中心,OZe轴指向地球极轴,OXe轴通过零子午线,OYe轴指向东经90°方向。
导航坐标系(n系):根据导航系统工作需要选取的导航基准坐标系,本文中选取东北天坐标系,即OXn轴指向东,OYn轴指向北,OZn轴指向天顶。
计算坐标系(n′系):由惯导计算得到的数学平台,与n系之间有三个平台误差角φe、φn、φu。
惯导坐标系(b系):原点在惯导重心,OXb轴、OYb轴、OZb轴分别沿惯导横轴向右、纵轴向前、立轴向上。
星敏坐标系(s系):原点在星敏感器重心,OXs轴、OYs轴、OZs轴分别沿星敏感器横轴向右、纵轴向前、立轴向上。
几个坐标系的位置关系如图1所示。

图1 坐标系间的位置关系Fig.1 Positional relationship between coordinate systems
1.2 惯性导航系统模型
将惯导的误差量及惯性仪表的常值项误差作为状态量,由于惯导高度通道不稳定,需要外部阻尼,在建模时不考虑高度和天向速度,则有
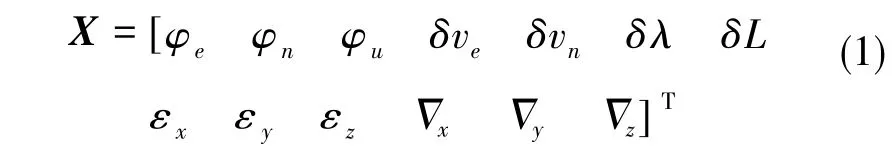
式(1)中,φe、φn、φu为姿态误差角,δve、δvn为速度误差,δλ、δL为经度误差、 纬度误差,εx、εy、εz为陀螺仪随机常值漂移,为加速度计随机常值偏置,下标e、n、u表示变量在n系三轴的分量,下标x、y、z表示变量在b系三轴的分量。
基于惯导误差方程,惯导系统的状态方程可表示为
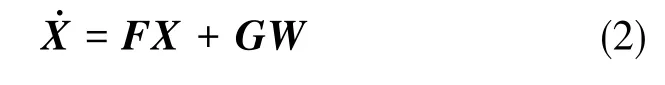

式(3)中,ωie为地球自转角速度,vE、vN、vU为东向速度、北向速度、天向速度,L为纬度,h为高度,fE、fN、fU为东向比力、北向比力、天向比力,RM、RN为子午圈半径和卯酉圈半径。
1.3 卫星导航系统观测模型
卫星导航系统能够提供速度、位置信息,其观测量为

量测方程如下

式(5)中,Xk即为式(1)所示状态向量,为卫星量测噪声。
1.4 天文导航系统量测模型
机载天文导航系统一般采用小视场星敏感器,其输出为恒星在星敏系和地球系的矢量坐标。选取恒星在惯导系的矢量坐标为滤波观测量,则有

式(6)中,Sb=[SbxSbySbz]T为惯导系矢量,可由星敏感器输出的星敏系矢量通过安装误差矩阵转换得到;为惯导系矢量真值;VCNS为测量噪声。 其中,Se=[SexSeySez]T为地球系矢量真值,可通过惯性系矢量和绝对时间计算得到。为惯导姿态矩阵(可由惯导实时解算得到),为导航系到计算系的转换矩阵,为地球系到导航系的转换矩阵真值。
可用惯导解算的经纬度λI、LI和经纬度误差δλ、δL表示,有
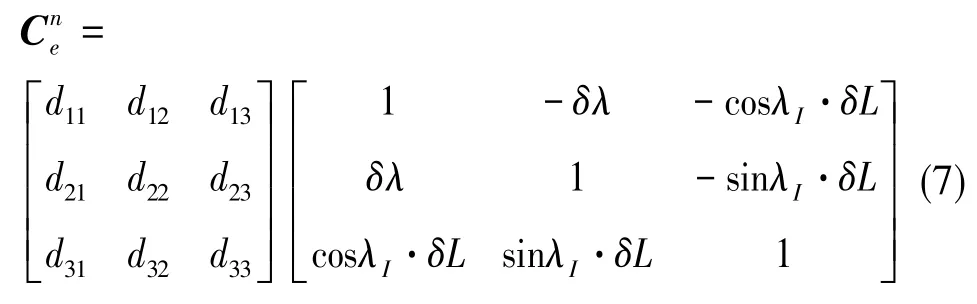


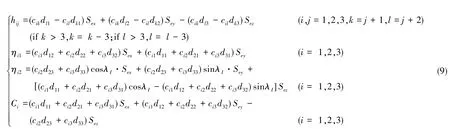
一般情况下,卫星导航系统输出频率为1Hz,天文导航系统输出频率更低,两者均低于惯导更新频率。因此,卫星天文辅助惯导空中对准是一种异步多源信息融合问题。对多源信息融合,一般采用集中滤波、联邦滤波或者传统意义上的序贯滤波进行处理。这些滤波方法均要求各信息源统一到同一时刻,需要进行内插外推,这不仅会造成精度损失,还会增加算法复杂度和计算量。为此,本文将序贯滤波算法进行推广,使其在无需对观测信息进行处理的前提下适用于异步多源信息融合系统。
2 广义序贯滤波算法
传统意义上的序贯滤波算法是为降低高维数观测向量情况下滤波算法的计算量而使用的处理方法。通过将观测更新中对Zk的集中处理分散为对Zk的各分量组的顺序处理,有效地降低了计算量,同时增强了算法可重构性,即当测量装置中某个或某几个传感器突然中断时,滤波器还可以利用测得的信息继续工作,实现了量测信息的即插即用。观测向量的序贯处理只在量测更新中进行,因此要求所有观测信息在同一时刻[8]。
传统序贯滤波算法的局限性在于:在滤波时刻仅进行一次状态更新,然后对多组量测信息进行序贯处理。若可以在任意一组观测信息到来的时刻均进行一次状态更新和量测更新,则可避免将所有传感器信息统一到同一时刻。由于不同量测信息均是针对同一组状态变量进行估计,该滤波算法本质上依然是对不同时刻的量测信息进行了序贯处理,故在此称之为广义序贯滤波算法。
设某个异步信息融合系统有l个量测系统,第i(i=1或2或…或l)个、 第j(j=1或2或…或l)个量测系统分别在k-1时刻、k时刻产生量测信息,将其观测向量表示为设基于k-2次观测向量集合可为任意量测系统输出,在此缺省上标)得到的线性最小方差估计为那么基于估计Xk-1而得到的一步最优线性预报为
其中,符号表示正交投影[8]。 在 获 得后, 滤波估计为然后到k时刻, 在获得后,要重新计算状态更新一步预测值进而从Xk,k-1和计算得到
可见,广义序贯滤波算法可以通过在量测信息到来时刻顺序进行状态更新和量测更新来实现异步多源信息融合,既解决了时刻统一带来的精度损失问题,又保留了传统序贯滤波算法即插即用的优点。在第j个量测系统产生量测信息的k时刻,广义序贯滤波过程如下
(1)状态一步预测

(2)状态一步预测均方误差

(3)进行量测更新
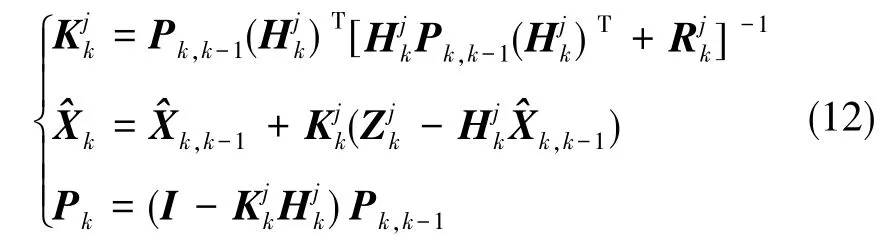
将广义序贯滤波应用于卫星天文辅助空中对准,当卫星或天文导航系统在不同时刻获得量测信息后,系统都会在上一次更新的基础上进行更新,从而使得每个辅助系统的量测信息都在状态估计中发挥作用。广义序贯滤波可实现卫星、天文导航系统的优势互补,使状态量在较短时间内达到最小方差估计。本文所提出的卫星天文辅助空中对准算法,其广义序贯滤波过程如图2所示。

图2 INS/CNS/GNSS广义序贯滤波示意图Fig.2 Schematic diagram of generalized sequential filter in INS/CNS/GNSS
3 仿真验证
由于星敏感器一般在载机巡航阶段及平台角速度小于5(°)/s的情况下工作,故选用飞行较为平稳的一段真实飞行数据进行空中对准仿真,所采集的飞参数据包含载机姿态角、航向角、惯性导航速度和位置、卫星导航速度和位置等信息。仿真时,使用起始时刻姿态角、航向角、卫星导航速度和位置信息作为初值,使用姿态角、航向角、卫星导航速度的变化率作为轨迹发生器的输入,来生成陀螺仪和加速度计的输出以及飞行参数的基准值。载机飞行曲线如图3所示,飞行轨迹特征点信息如表1所示。设定:陀螺仪常值漂移为 0.008(°)/h,白噪声为 0.004(°)/h,加速度计常值零偏为5×10-5g;卫星导航系统输出周期为1s,位置精度为20m,速度精度为0.2m/s;天文导航系统输出周期为3.5s,星矢量精度为3″,星敏感器视场为2°×2°,星敏感器与惯导安装误差标定后残余误差为5″。

图3 载机空中飞行曲线Fig.3 Curve of aerial flight
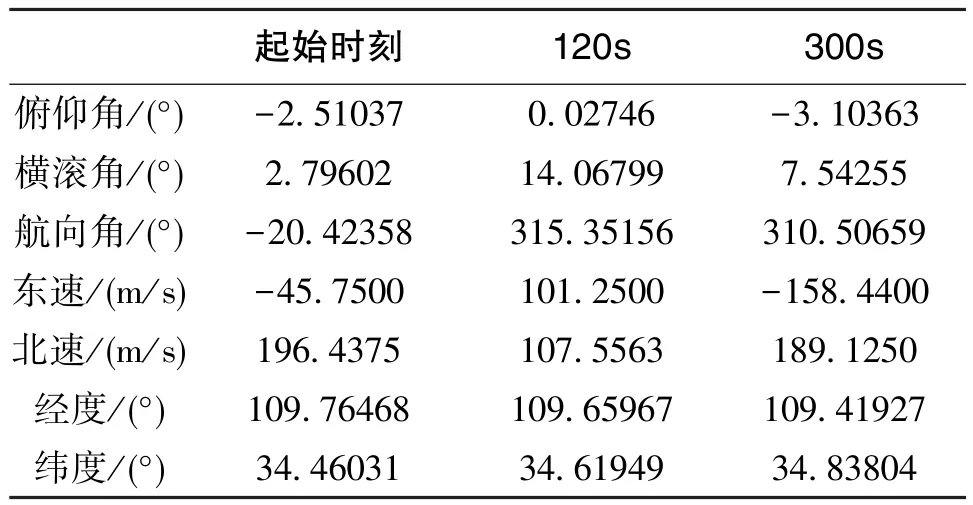
表1 飞行轨迹特征点信息Table 1 Feature point information of flight trace
星敏感器需要惯导为其提供精度0.05°之内的水平姿态信息和视场范围内的航向信息才可观测恒星。因此,所提对准算法的仿真分为两个阶段:1)大失准角修正阶段,利用卫星导航系统将俯仰角误差、横滚角误差修正到0.05°之内,将航向角误差修正到2°之内,采用分段修正的方式,总时间设置为90s;2)INS/CNS/GNSS 精对准阶段,同时使用卫星信息和天文信息对惯导误差进行精确修正,时间设置为30s。经过多次Monte Carlo仿真,对比于表1中的基准信息,对准误差统计如表2所示。

表2 对准误差统计Table 2 Statistical results of alignment error
图4给出了 INS/CNS/GNSS空中对准误差估计曲线。


图4 卫星天文辅助空中对准误差估计曲线Fig.4 Error estimation curves of CNS/GNSS aided in⁃flight alignment
可见,本文提出的基于广义序贯滤波的卫星天文辅助空中对准方法可在2min内完成高精度对准,俯仰角、横滚角和航向角对准误差均控制在0.004°之内。在第一阶段利用卫星辅助对准修正后,三个角度误差满足星敏感器观星条件。在引入天文量测信息之后,误差角快速收敛。
卫星天文共同辅助对准算法只有在满足星敏感器观星条件的飞行状态、天气情况下可达到所论述的对准性能,若对准过程中出现由于云层遮挡等原因造成天文量测信息不可用的情况,惯导依然可以在卫星辅助下完成空中对准,不会造成对准失败,这是由于算法采用了广义序贯滤波来处理多源信息融合,使得该对准算法具有较强的可重构性。然而,若此时第二阶段依然为30s,则失准角估计无法收敛,对准误差过大。表2中列出了 2min的 INS/GNSS对准误差,图 5给出了2min对准第二阶段30s有无天文信息估计曲线对比情况。基于此,在天文量测信息不可用时,须将整个对准时间至少延长至5min。经过多次Monte Carlo仿真,INS/GNSS对准误差统计于表2中,估计曲线如图6所示。需要说明的是,图6中速度误差和位置误差估值并非未收敛,而是在跟踪误差变化趋势。

图5 卫星天文辅助与卫星辅助误差估计曲线对比Fig.5 Comparison of error estimation curves between CNS/GNSS aided and GNSS aided
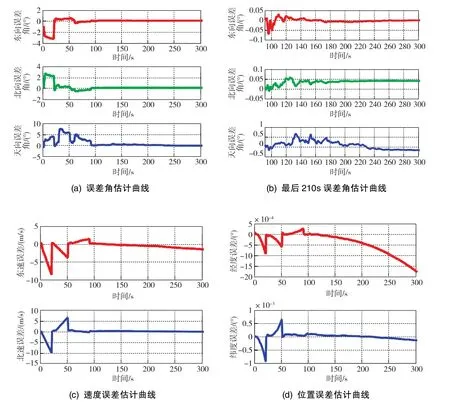
图6 卫星辅助空中对准误差估计曲线Fig.6 Error estimation curves of GNSS aided in⁃flight alignment
可见,相比于传统卫星辅助方法,本文提出的新方法大大提升了对准性能,对准时间缩短至2min。同时,对准精度也提高了1个数量级。
4 结论
在长航时远程飞机开始配备天文导航设备的背景下,为提升机载惯导空中对准性能,本文提出了一种基于广义序贯滤波的卫星天文共同辅助惯导进行空中对准的方法。广义序贯滤波算法一方面解决了卫星导航系统与天文导航系统异步输出的问题,另一方面也使算法有了较强的可重构性。本文首先建立了卫星天文辅助惯导空中对准的系统模型,然后对广义序贯滤波算法进行了说明,最后在真实飞行轨迹条件下进行了仿真。仿真结果表明,本文提出的方法能够将对准时间缩短为2min,同时将对准精度提高了1个数量级,在很大程度上提升了武器装备的快速反应能力和精确打击能力,具有较高的工程应用价值。
