三浮陀螺加速度计浮子六自由度运动分析

贺 宇，孙文利，冯毅博

（北京航天控制仪器研究所，北京 100039）

0 引言

三浮陀螺加速度计属于摆式积分陀螺加速度计 （Pendulous Integrating Gyroscope Accelerometer，PIGA），是一种利用陀螺力矩进行反馈的摆式加速度计［1］，具有陀螺仪和摆的双重特性。为了消去干扰力矩的影响，需要利用伺服、磁悬浮、温控等控制回路对浮子、框架的转动等进行控制，保证仪表的正常工作状态与输出精度。对浮子的六自由度建模分析可更好地描述其在浮液内的运动状态。稳定浮子质心位置，实现对浮子的六自由度控制，可提升仪表结构的稳定性，减小安装误差带来的影响，对提升、发挥三浮仪表的精度优势具有重要意义［2⁃3］。 在有横向加速度时，浮子的运动数据也对分析仪表输出方程中的各非线性项具有重要意义。

王雪等［4⁃5］对三浮陀螺的浮子进行了磁悬浮控制系统建模，并对其磁悬浮与温控回路进行了一体化设计，其模型涉及到陀螺仪浮子的五个自由度。唐哲［6］对三浮陀螺的浮子运动规律进行了建模与仿真分析，其分析主要涉及陀螺仪磁悬浮控制系统的五个自由度。吴辽等［7］在对三浮陀螺的磁悬浮结构进行优化设计时，对陀螺的浮子进行了动力学分析。

转子陀螺仪的浮子具有对称性，无偏心质量，在上述提到的已有工作中，对其建模分析仅包含磁悬浮系统所能控制的五个自由度。而三浮陀螺加速度计的浮子具有偏心质量，目前并未有此类对其浮子运动状态的理论建模。对三浮陀螺加速度计工作原理的动力学分析往往将其简化为带偏心质量的双框架二自由度陀螺仪，内外框架间只存在内环轴的旋转角度一个自由度，并主要分析双框架绕各自旋转轴的角运动。针对上述分析中陀螺仪的浮子动力学模型仅有五个自由度的不足以及未有对三浮陀螺加速度计带有偏心质量的浮子模型进行建模的不足，本文考虑了三浮陀螺加速度计的浮子在浮液内有平动与转动共六个自由度的相对运动，从而可建立更为完整的三浮陀螺加速度计工作原理模型，以更好地描述运动状态，并可据此实现对浮子的六自由度调整，从而稳定了浮子位置，确保了模型的准确性，提升了整表精度。因此，本文以可六自由度运动的浮子以及包含浮子组件在内的外框架为研究对象，建立了完整的动力学模型。在无横向加速度时，对模型进行线性化，根据线性化模型，通过互相解耦的控制回路与一体化的控制系统对浮子进行了六自由度调整试验；在有横向加速度时，对浮子的非线性耦合运动进行了分析，并通过试验获取了相关数据。

1 动力学分析

如图1所示，分别建立固连在浮子的坐标系O2X2Y2Z2（内框系）、固连在外框架上的坐标系O1X1Y1Z1（外框系）、固连在加速度计外壳体的坐标系O0X0Y0Z0（基座系）。陀螺角动量为H，浮子组件质量为m，在浮液内可自由运动，其质心位于O2X2Y2Z2坐标系的l＝［0 0l］T处，将其在浮液内的运动分解为以O2为基点的平动和定点转动，浮子组件长度为L（沿O2Y2轴），浮液浮力Ff等效作用于O2处。

图1 三浮陀螺加速度计原理图Fig.1 Principle diagram of PIGA

根据三浮陀螺加速度计的工作环境，设外壳体相对惯性空间保持固定姿态即无相对角速度［8］。设外框架绕外框轴的进动角速度为，浮子在浮液中相对外框架的转动角度分别为θx、β、θz，转动角度角秒量级，对转动顺序无要求，在O2X2Y2Z2与O1X1Y1Z1的投影相同。从O1X1Y1Z1坐标系到O2X2Y2Z2坐标系的姿态转换矩阵为Cnw， 同理由于3个转动角度均较小，对正余弦做近似处理可以得到，无论在何种转动顺序下均有

理想状况下，浮子组件在O2X2Y2Z2坐标系的转动惯量为：J2＝diag（J2x，J2y，J2z）； 外框架在O1X1Y1Z1坐标系的转动惯量为：J1＝diag（J1x，J1y，J1z）。浮子组件整体的角动量投影在O2X2Y2Z2上为：为浮子组件相对惯性空间的角速度；外框架的角动量Hw投影到外框系O1X1Y1Z1时：为外框架相对惯性空间的角速度，

首先以浮子为研究对象，将浮子运动分解为相对外框架坐标系O1X1Y1Z1的平动与绕自身固连系O2X2Y2Z2原点O2的定点转动，根据动量守恒与角动量守恒定理，列出的矢量表达式为

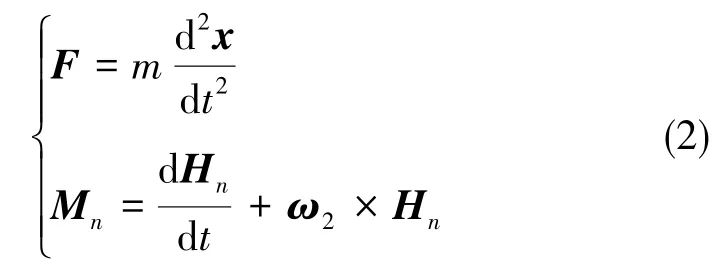
式（2）中的第一个矢量方程为平动方程，投影在外框系O1X1Y1Z1上，x为浮子相对外框架的位移矢量。F为浮子的外力矢量和，浮子组件受到浮液的浮力Ff、磁悬浮磁拉力（左端径向磁力Fxl、Fzl，轴向磁力Fy，右端径向磁力Fxr、Fzr）、 惯性加速度a0产生的力（a0为外壳体的视加速度在O0X0Y0Z0坐标系的投影）、浮液阻尼的作用力。还应考虑外框架转动带来的牵连加速度以及科氏加速度产生的惯性力-MA1，其加速度

式（2）中的第二个矢量方程为以基点O2为中心的定点转动方程，投影在内框系O2X2Y2Z2上，Mn为磁悬浮拉力产生的力矩、相对角运动浮液阻尼力矩、各惯性力矩（基座加速度a0引起的惯性力矩Mn1，外框架转动、浮子与外框架的相对运动产生的惯性力矩Mn2）的矢量和，由于浮心位于原点O2处，因此浮力不产生力矩。其中，磁悬浮拉力产生的力矩在O1X1Y1Z1上的投影Mcxf＝可转换到O2X2Y2Z2坐标系，外框架转动、浮子与外框架间的相对运动带来的惯性力矩Mn2可展开写为

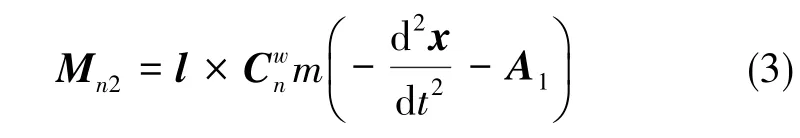
同理，以外框架（包含内部浮子组件）为研究对象可得转动矢量方程

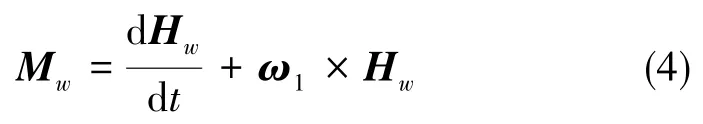
式（4）中，Mw应包含基座的加速度带来的惯性力矩Mw1、沿O1X1轴的干扰力矩MX1以及电机力矩-MD。此处使用自由刚体的运动模型，不考虑内部浮液流动的干扰，则将上述浮子的2个矢量方程展开，并求出外框矢量方程沿OX1的分量，可得

ABS树脂的增韧机理为多重银纹及剪切带，橡胶粒子诱发银纹并阻止银纹的发展，多个橡胶粒子互相作用形成多重银纹，吸收能量，材料表现出韧性。当温度提高到一定程度，高分子之间自由空间加大，分子链段运到能力提高，分子链更加容易取向，在外力作用下更多的分子参与形变，形成剪切带，提高材料抵抗外力的能力。

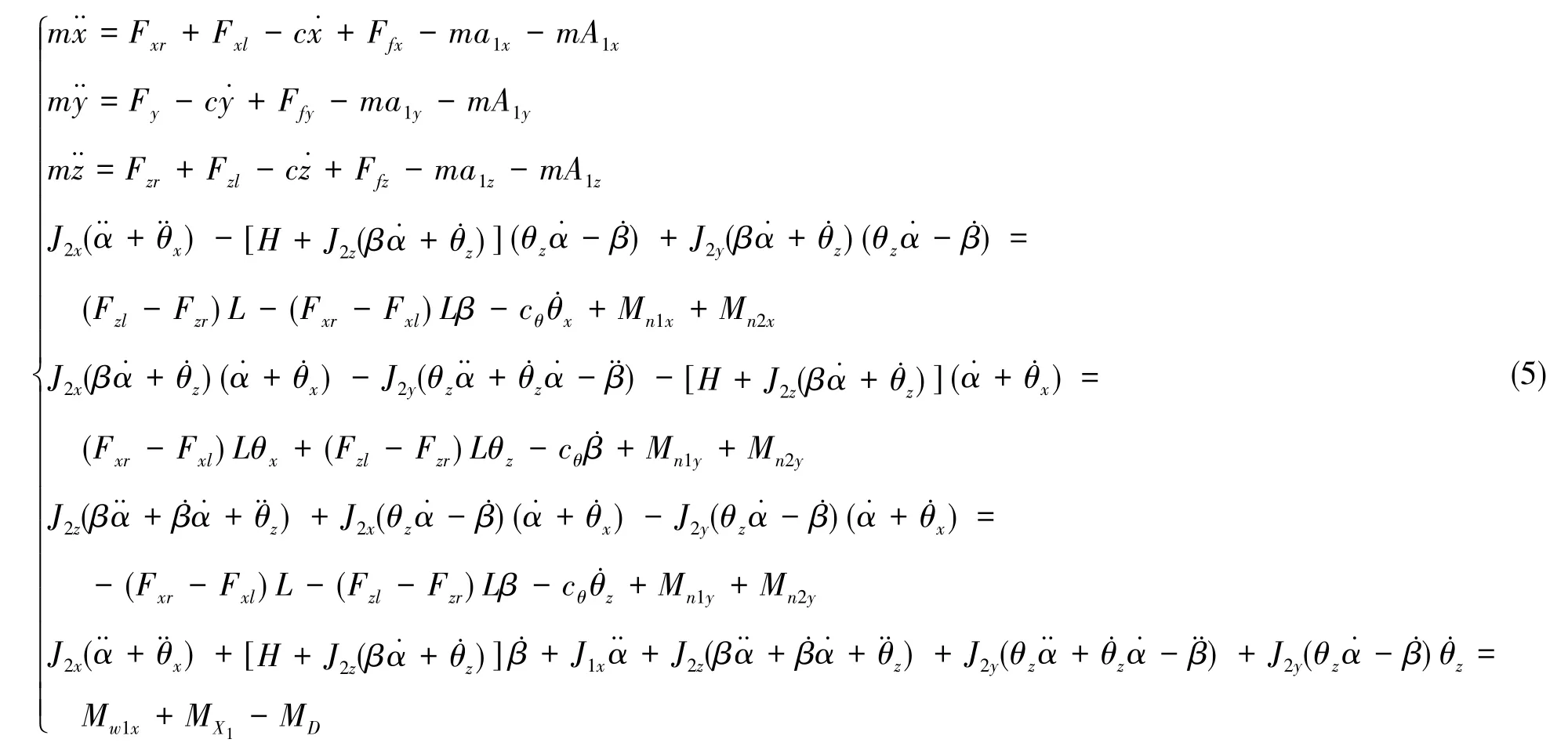
式（5）中，c为浮液对浮子做相对线运动的阻尼系数，cθ为浮液、 浮子做相对角运动的阻尼系数，a1＝［a1xa1ya1z］T为基座加速度a0在O1X1Y1Z1的投影。

2 基座加速度对模型的影响分析

2.1 非线性耦合运动分析

在基座加速度a0＝［a0xa0ya0z］T即有横向加速度a0y、a0z时，内框架惯性力矩Mn1为

外框架惯性力矩Mw1为

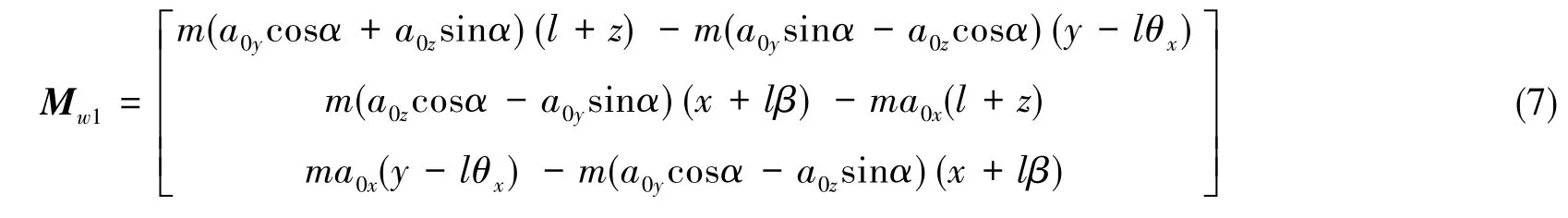
由于浮子与外框架间的位移为微米量级，浮子在浮液内的角运动为角秒量级，与其他量相比相对微小，且采用了阻尼系数c与cθ较大黏稠浮液，故舍去式（5）中等式右侧含有与x或［θxβθz］T乘积的力与力矩，且可忽略式（5）中等式左侧的角度变量二阶及高阶乘积小量，则可得内框架惯性力矩为

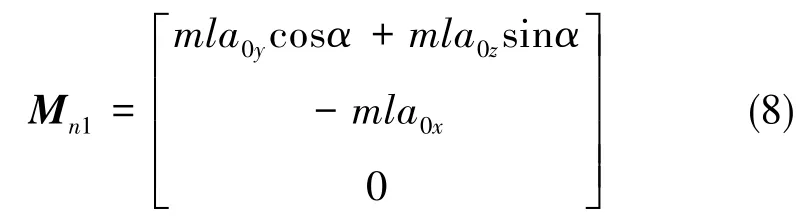
外框架惯性力矩沿O1X1的分量为

可得方程组

由于外框架的进动，式（10）中的输入力矩为式（7）、式（9）中的周期性力矩，无法线性化。由于平动方程与转动方程右侧受力、力矩项与外框架进动项有关，同时各自由度间有较强的相互耦合［9］，因此在输入加速度固定时，浮子最终将呈现出周期性的运动，各自由度运动周期与进动周期一致。

2.2 模型线性化与静态解耦分析

考虑到浮液可在温控回路的控制下保持温度稳定［10］，则在浮子的平动方程中，浮力将与各惯性力达到平衡，于是浮子的外力矢量和F可简化为磁悬浮拉力与相对线运动引起的浮液阻尼力的矢量和。在基座无横向加速度即惯性力只有沿O0X0的分量时有由上述分析可得内框架惯性力矩因此，可实现对方程组的线性化

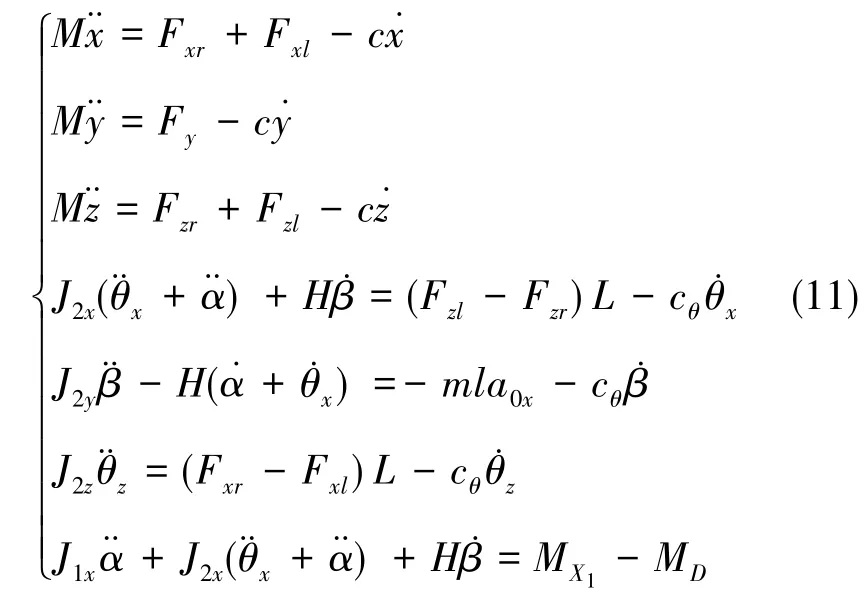
据此建立整个控制系统的状态方程

选取13维状态变量和7维输入量

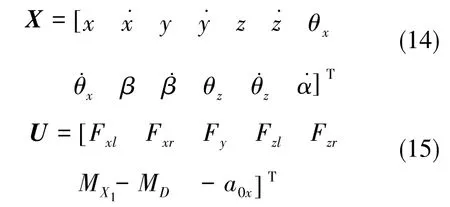
可得系统矩阵A13×13和矩阵B13×7

选取7个方便观测的输出量

各变量分别为：浮子左右端沿X1轴的位移xl和xr、沿Y1轴的位移y、左右端沿Z1轴的位移zl和zr、内环轴转动角β、外环轴进动角速度̇α，可得输出方程

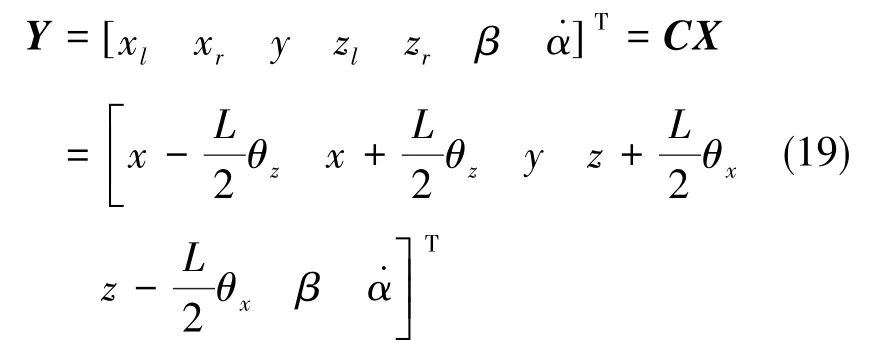
则有

对上述系统进行分析，可求得

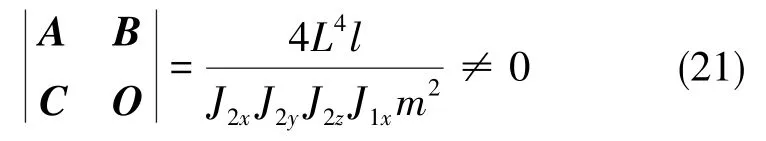
因此对应矩阵满秩，则式表明上述系统满足静态解耦条件，7个输出量在一定条件下，稳态时由对应的输入量所控制。输入输出量中的前5个与磁悬浮回路相关，其余2个输入输出量与伺服回路相关，此外为保证浮液提供的浮力以及相对运动、相对角运动的阻尼系数稳定，需要温控回路控制浮液温度。因此，通过三浮陀螺加速度计的温控、磁悬浮与伺服三条回路相互配合控制，可实现对上述7个变量的调整。浮子的六自由度通常为3个平动自由度与3个转动自由度，即状态变量中的以下六维

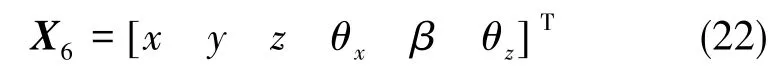
通过可逆转化矩阵

可将其转换为输出量中的前六个变量

即Y6＝C6X6， 由于转化矩阵可逆-L2/2），因此上述两种六自由度完全等价。而Y6中的前5个变量即磁悬浮回路所控制的浮子径向、轴向的位移，第6个变量对应伺服回路中的内环角度。因此在温度稳定的条件下，通过发送通信指令可对上述6个自由度进行调整。

3 试验结果与分析

3.1 斜置试验

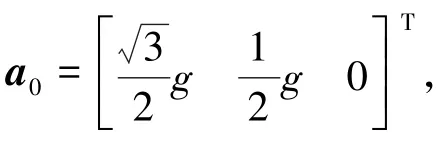
图2 横向加速度造成的浮子周期性运动Fig.2 Periodic motion of floater caused by lateral acceleration

由该浮子位置可得表1。

表1 浮子斜置试验状态分析Table 1 State analysis of floater inclined experiment

根据式（10），由于其非线性耦合性较强，此处仅分析由于外框架进动产生的周期力矩、周期力而导致浮子各自由度呈现的周期运动是否一致的问题。进动周期的设计值为6.60s，显然各自由度运动周期基本与外框架进动周期一致，测试结果与该方程组特性一致。

3.2 六自由度调整试验

为验证在无横向加速度时的线性化模型以及静态解耦特性，对浮子进行六自由度调整试验，试验使用上述进行了小型一体化控制回路设计的某型号三浮陀螺加速度计以及程控多齿分度台ZDFT⁃720。为验证静态解耦与六自由度调整，利用分度台使得仪表输入轴O1X1与当地水平面夹角为180°，此时加速度输入a0＝［-g0 0］T， 通过上位机对一体化控制系统发送指令，对浮子6个自由度进行调整，可得到如图3所示结果。在整个测试过程中，在不同时间分别使用上位机对一体化控制系统发送相应的调整指令，观察各自由度的调整结果，判断是否可实现静态解耦以及对六自由度的调整，调整自由度时发送的指令内容以及调整后的状态分析如表2所示。

图3 浮子六自由度调整试验结果Fig.3 Results of floater 6⁃DOF adjustment experiment

表2 浮子六自由度调整试验指令、状态分析Table 2 Command and status analysis of floater 6⁃DOF adjustment experiment

分析浮子六自由度位置状态的图表可知：在过渡过程中，浮子各径向位移之间有耦合作用；各平动位置变量在过渡时间后与其稳态误差大部分均小于0.06μm，该值小于磁悬浮控制回路的死区范围，转动位置的误差小于5″，该值接近内环角度传感器的死区范围。因此，在稳态时浮子径向轴向位移、内环角度共6个自由度均能达到设定值，可实现静态解耦对浮子的六自由度调整。

4 结论

本文以可六自由度运动的浮子与外框架为分析对象，建立了三浮陀螺加速度计的工作原理动力学模型，根据有无横向加速度输入，对浮子的六自由度运动特性进行了分析。在有横向加速度输入时，可得由于进动导致的周期性力矩、周期力，浮子各自由度均将做周期运动，通过斜置试验得到了浮子的周期性运动数据，验证了浮子各自由度均呈现出与陀螺摆进动周期一致的简谐运动的结论。在无横向加速度输入时，可对动力学方程组进行线性化，分析可知模型具有静态解耦特性，据此通过小型一体化控制系统对仪表进行试验，试验实现了对浮子的六自由度调整，验证了浮子六自由度运动的可静态解耦特性。