青年男性慢速自重抗阻训练能量消耗的模型构建与准确性评估

杨丽君 吴丹 郑雪芹 何享波 陈庆果

青年男性慢速自重抗阻訓练能量消耗的模型构建与准确性评估

杨丽君，吴 丹，郑雪芹，何享波，陈庆果

摘 要：目的：研究不同重复次数慢速自重抗阻训练的能量消耗水平，构建不同动作自重抗阻训练的能量消耗方程，为运动能量消耗的自我监控与科学健身提供实证参考。方法：选取40名健康男性受试者作为测试对象（建模组30人和验证组10人），采用Cosmed K4b2便携式心肺功能仪分别测量受试者3个不同抗自重动作（标准俯卧撑、站姿提踵以及自重深蹲）在6种重复次数下的能量消耗值。运用重复测量设计的方差分析检验能量消耗和心率的被试内差异，使用逐步多元回归分别构建总能耗模型和不同动作能耗模型，采用Pearson 相关分析和Bland-Altman polt等方法评估各模型的整体准确性及不同重复次数下的预测效度。结果：（1）相同重复次数下，3个自重抗阻运动两两之间在能量消耗、心率指标上均存在显著性差异（P<0.05）。（2）总模型：EEm（每分钟能量消耗，energy expenditure per minute，简称EEm）=0.153×重复次数+0.061×心率+0.028×体重-4.656。（3）不同动作模型：EEm（俯卧撑）=0.441×重复次数+0.055×身高+0.025×心率+0.031×体重-11.111;EEm（提踵）=0.104×重复次数+0.013×身高+0.009×心率+0.005×体重-1.714;EEm（深蹲）=0.448×重复次数+0.024×身高+0.016×心率+0.018×体重-4.882。结论：以身高、体重、心率及重复次数4个变量构建的能耗预测方程，能够较为准确地预测慢速自重抗阻训练的运动能耗，可为普通大众运动能量消耗的自我监控与科学健身提供实证参考。

关键词：抗阻训练;自重抗阻运动;体力活动;能量消耗;模型

中图分类号：G808.16   文献标识码：A  文章编号：1006-2076（2021）05-0091-12

Model construction and validity test of energy consumption in slow self-weight resistance training with different repetition times

YANG Lijun， WU Dan， ZHENG Xueqin ， HE Xiangbo， CHEN Qingguo

School of Physical Education， Sichuan Normal University， Chengdu 610101， Sichuan，China

Abstract：Objective： To study the energy expenditure levels of different repetition times of slow self-weight resistance training， construct the energy expenditure equation of self-weight resistance training of different movements， and provide empirical reference for the self-monitoring of sports energy expenditure and scientific fitness. Methods： 40 healthy male samples are selected as test subjects （30 in the modeling group and 10 in the verifiable group）， and the Cosmed K4b2 portable cardiopulmonary function instrument is used to measure the subjects′ 3 different anti-weight actions （standard push-ups， standing heel lifts and self-weight squats） energy expenditure value under 6 repeated times. The variance analysis of the repeated measurement design is used to test the differences in energy expenditure and heart rate among the subjects. The stepwise multiple regression is used to construct the total energy expenditure model and the energy expenditure model of different actions. Pearson analysis related and Bland-Altman polt are used to evaluate the performance of each model. Overall accuracy and predictive validity under different repetition times. Results： 1） Under the same number of repetitions， there are significant differences in energy expenditure and heart rate between the three self-weight resistance exercises （P<0.05）. 2） Total model： EEm （energy expenditure per minute， EEm for short）=0.153*number of repetitions + 0.061*heart rate+0.028*weight-4.656. 3） Different action models： EEm （push-ups）=0.441*repetition times+0.055*height+0.025*heart rate+0.031*weight-11.111; Eem （heel lift）=0.104*repetition times+0.013*height+0.009*heart rate+0.005*weight -1.714; EEm （squat）=0.448*number of repetitions+0.024*height+0.016*heart rate+0.018*weight-4.882. Conclusion： The energy expenditure predicting equation， with four varieties of height， weight， heart rate and repetition times can more accurately predict the energy expenditure of slow self-weight resistance training， which can be used for providing empirical reference for self-monitoring of sports energy expenditure and scientific fitness for the general public.

Key words：resistance training; self-weight resistance exercise; physical activity; energy expenditure; model

抗阻训练被认为是刺激肌肉增长与力量增加、促进能量消耗、延缓肌肉萎缩[1]、改善运动素质以及预防慢性疾病[2]的有效方法，近年来，抗阻训练在中国乃至全球范围内都是健身领域的热门健身趋势。美国运动医学协会（American College of Sports Medicine， ACSM）[3]推荐健康成人需完成每周2～3次、每次至少1组、每组8～10次重复的抗阻训练。在抗阻训练中“力量与速度的关系”是影响训练效果的关键因素之一[4]，向心或离心阶段持续2 s～6.5 s的慢速抗阻训练已被证明能更有效地促进神经肌肉支配的能力，并对缺乏训练经验的人群发展运动技能更有帮助，而自重抗阻训练因其便利性、安全性而备受推崇，越来越广泛地应用于大众健身及医疗康复领域，尤其是包括健身初学者、普通老年人以及临床在内的群体。

如何科学监控抗阻训练过程中的能耗问题一直是体力活动测量领域的核心和难点，运用科学的方法测量能耗对于评定运动效果与指导科学健身具有重要意义[5]。在实践层面上，由于能量消耗的测量仪器具有设备复杂、价格昂贵及操作困难等特点，且多局限于实验室使用，大众健身效果的即时评价因而受到制约。故寻求一种高效、经济的能量消耗评定方法是学者们一直以来想要攻克的难题。在理论层面上，早在20世纪80年代初，已有研究试图尝试量化抗阻运动能量消耗，Wilmore等人[6]首次采用间接测热法来测定运动过程中的能耗以及运动后的过量氧耗（EPOC），以此来推算运动能耗，开创了抗阻运动能耗量化领域的先河。后来不断有学者证明EPOC的大小取决于运动强度[7]、运动时间[8]、组间休息时间、运动前的营养补给[9]以及训练状态[10]等因素，这一系列研究推翻了通过EPOC估算抗阻运动能耗这一研究思路，认为仅在运动后测量摄氧量（VO2）并将其带入到运动过程中，并不能准确反映抗阻运动的真实代谢成本。近年来，数学模型逐渐应用于预测体力活动能量消耗中，为学者们解决能耗的测量与评定问题提供了一个新的思路。例如，Robergs等人[11]将负重量和距离代入回归方程建立计算VO2的模型，结果表明所代入的2个变量共可分别有效解释卧推、平行蹲能耗的72.8、65.6的变异量，Lytle等人[12]有关抗阻能耗预测研究也有类似结果。但目前来看，对此类模型的探究结果还相对较少，还需更多的实证依据以形成概化性的结论。

纵观以往研究发现，国外侧重于传统自由重量或高负荷负重器械的能耗建模研究，国内对健身有效能耗预测的模型构建又相对集中在走跑类、生活方式类等有氧运动方面，而对抗阻运动的能耗预测涉及极少，并且关于大众抗阻训练能耗量化评价标准方面的研究鲜少见报，缺乏指导大众科学健身锻炼的抗阻训练运动处方的实验研究。因此，有必要丰富以数学模型为基础的抗阻训练能耗预测方程。本研究采用气体代谢的精确短时热量测定方法的金标准[13]——间接测热法（indirect calorimetry，简称IC）测定机体的能量消耗，以普通健康成年男性为测试对象，分别测量受试者3个不同抗自重动作（标准俯卧撑、站姿提踵以及自重深蹲）在6种重复次数下的能量消耗值，并使用逐步多元回归分析分别构建总能耗预测模型和不同动作能耗预测模型，且对各模型的测量准确性进行效度检验，旨在为大众健身人群運动能耗的自我监控及运动处方（方案）的优化提供证据支撑。

1 研究对象与方法

1.1 研究对象

通过G*Power 3.1.9.7软件进行样本量计算[14]。研究采用3（动作）×6（重复次数）的实验设计，通过预实验数据确定I型错误概率（α）为0.05，效果量为0.20，统计功效为0.85，统计分析方法采用双因素重复测量方差分析，最终样本量确定为40名测试对象。

选取40名普通健康青年男性作为测试对象，测试前随机将其分为建模组（30人）和验证组（10人）。2组受试者的形态学指标无显著差异（P>0.05）（基本信息见表1）。所有受试者无心血管、肺部疾病或神经系统疾病等病史，且均有规律的运动习惯（每周1～3次），测试前无大强度运动且未服用咖啡、刺激性饮料等，并维持正常生活作息。测试之前均签署知情同意书，熟悉本研究实验流程。

1.2 研究方法

1.2.1 测量指标与仪器

采用恒康佳业HK-6000身高体重仪测试受试者的身高体重（分别精确到0.1 cm/kg），使用清华同方身体成分测试仪测量身体质量指数（BMI）以及体脂率（）。

采用意大利生产的Cosmed K4b2心肺功能测试仪收集受试者的每分钟气体代谢指标，包括VCO2、VO2、RER等数据指标[15]。为保证测量的精度，整个测试前更换氧电池，每天测试之前均对仪器进行预热和校准。采用芬兰产Polar H10心率胸带通过Polar心率接收器连接至Cosmed K4b2同步检测心率（HR）指标。每次测试完成后，将数据保存为*.xpo格式，后期再转制为周期为

60 s的数据库。

1.2.2 测试方案

本实验采用随机交叉设计对40名普通健康青年男性分别进行2次慢速自重抗阻训练测试。2次测试的间隔时间为1天，所有的被试在同一周、不同天的同一时间内完成，尽可能地避免测量误差。受试者在测试前一天内无大强度运动，且测试前1 h不再进食。所有测试均在实验室环境进行，测试时间为08：30—11：30，14：30—17：30和18：30—21：30。测试环境湿度为50±10，温度为20.7℃±0.9℃，2次测试的温度、湿度指标无显著性差异（P>0.05）。

正式测试前，安排受试者进行有针对性的热身活动，受试者需佩戴心肺功能测试仪器K4b2呼吸面罩和心率带适应后先静坐5 min再连接主机开始测试（如图1所示）。

自重抗阻训练能耗测试方案：本研究选取大众健身最常练习的3个自重抗阻动作——标准俯卧撑、站姿提踵及自重深蹲，这3个动作覆盖了人体主要的上下肢肌群。其中，俯卧撑主要锻炼上肢、腰腹部位的肌肉，深蹲是增强腿部、臀部力量和围度以及发展核心力量的常见动作，提踵作为简单的单关节运动，主要锻炼小腿腓肠肌，其所涉肌肉与俯卧撑、深蹲动作互不产生影响，但俯卧撑、深蹲两动作均涉及核心肌群[16]。为了消除动作执行顺序的影响，受试者第1次测试完成俯卧撑，第2次测试先完成提踵再完成深蹲，共完成2次测试，2次测试的顺序随机。不同重复次数的阶段测试时间（如表2所示）。

具体步骤如下：首先，受试者静坐10 min，在静息测试时受试者需保持情绪平静、身心松弛的自我感觉最佳的状态;随后按照设定好的顺序完成6个不同重复次数（重复次数分别为1 reps /min、2 reps /min、3 reps /min、4 reps /min、5 reps /min、6 reps /min）的阶段测试（如图2所示）。每个重复次数的阶段运动4 min，俯卧撑动作每个阶段间进行3 min的休息恢复期间隔，提踵与深蹲动作的阶段之间用1 min的休息恢复期间隔，兩动作之间休息3 min。测试助手注意提醒受试者控制训练动作节奏为3 s上升、3 s下降，并准确记录每项动作的开始时间、结束时间以及阶段间的休息时间，且严格控制每次测试时的一致性。

测试技术动作遵循美国国家体能协会的规范标准，动作完成分为三个阶段：准备阶段、下降阶段及上升阶段。如图3所示：（1）俯卧撑：准备阶段训练者用双手接触地面支撑身体，双上肢垂直于地面，两腿向后伸展，头部、颈部、后背、臀部以及双腿在一条直线上;下降阶段两个肘部向身体外侧弯曲，身体收紧降低至基本靠近地面，两眼目视前方，收紧腹部，保持身体在一条直线上;上升阶段双肘匀速伸展至手臂伸直，还原为起始位置[17]。（2）提踵：准备阶段两眼平视前方、两脚与肩同宽、身体保持直立、膝盖与脚尖方向一致;上升阶段训练者踮起脚尖，在自己的极限处感受小腿肌肉的紧张;下降阶段训练者在1秒的小腿紧缩后，慢慢向下恢复到起始姿势。（3）深蹲：仅承担自身体重的深蹲训练被称为自重深蹲（Bodyweight squat，BW squat）[18]。准备阶段训练者两眼目视前方，两脚跟与肩同宽、身体直立、掌心相对、膝盖与脚尖方向一致;下降阶段训练者弯曲膝盖并降低臀部至大小腿夹角约为90°且大腿与地板平行;上升阶段双下肢均匀发力，缓慢推离身体还原为站姿位置。在整个深蹲过程中，要求膝关节不超过脚尖且保持中立位，该基本要求基于美国体能协会对深蹲运动的意见书[19]中的要求制定。

1.3 数据处理与分析

数据处理时，首先将前期从K4b2软件中导出的“*.xpo”文件分别转制为周期为60 s的数据库，并按照前期分组名单将其分为建模数据库和验证数据库。其中，每个阶段最后2 min或最稳定的连续2 min的数据用于受试者的VCO2、VO2、RER等指标，通过VCO2和VO2指标计算呼吸商（respiratory quotient，RQ），并采用经典的weir方程[20]计算能量消耗（energy expenditure，EE）：kcal·min-1=[（1.1×RER）+3.9]×VO2L·min-1。每个静息期间最后5 min或最稳定连续5 min的平均值作为静息的EE，每个阶段的平均心率来代表该阶段受试者的心率（HR）。

数据使用Microsoft Office Excel 2017和SPSS 20.0进行统计处理，所有结果均表示为平均数±标准差（M±SD）形式，各项测试数据采用Shapiro-Wilk法、Studentized Residual分析进行正态分布检验，判断有无异常值。运用重复测量设计的方差分析检验3个不同抗自重动作（俯卧撑、提踵和深蹲）在6种重复次数下的能耗和心率的被试内差异。使用逐步多元回归分别构建总能耗模型和不同动作能耗模型。

模型验证时，将验证组10名与本次实验测试对象情况基本一致的受试者身体指标数值代入能耗推算公式得到能耗预测值，比较预测值与实测值的差别，用以验证能耗模型的预测性能。采用 Pearson 相关检验预测方程的有效性。使用 Medacle 12.0软件绘制 Bland- altman plot图比较各模型在整体上预测值和实测值之间的一致性。采用SPSS 软件计算总模型和各动作模型的均方根误差（root- mean-square error，以下简称RMSE）、平均绝对百分误差（mean absolute percentage error，MAPE）及平均百分误差（以下简称Bias），进行比较各模型的测量准确性。统计分析中显著性水平定义为P<0.05。

2 研究结果

2.1 慢速自重抗阻训练的能耗特征及心率状况比较

利用Shapiro-Wilk法、Studentized Residual分析对原始数据进行检验，各项数据P值均大于0.05，无异常值，说明各数据观测值均服从近似正态分布。本研究中的不同抗自重动作和重复次数都是类别变量，检验变量分别为EE和HR，结合数据获取的被试特征，采用双因素重复测量的方差分析进行交互效应和主效应的检验。

2.1.1 动作×重复次数的交互效应分析

从表3可以看出，检验变量不论是EE还是HR，动作和重复次数的交互项均存在统计学意义，EE：F（10、290）=127.982，P=0.002，HR：F（10、290）=181.135，P=0.001，表明重复次数与不同动作之间存在着交互效应。

2.1.2 动作和重复次数的主效应分析

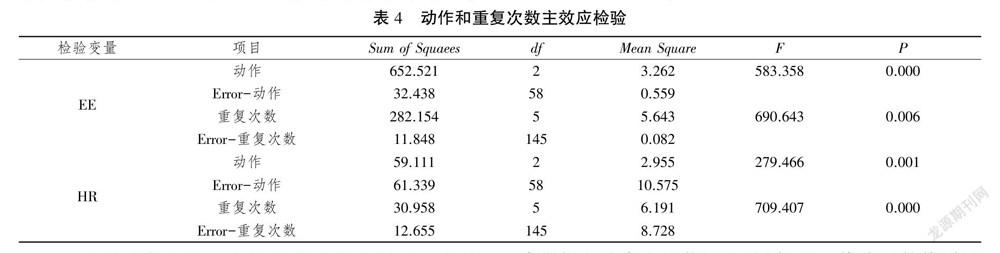
表4为主效应检验结果，动作、重复次数2自变量与检验变量EE之间的主效应均存在统计学意义，动作：F（2、58）=583.358，P<0.001，重复次数：F（5、145）=690.643，P=0.006。动作、重复次数2自变量与检验变量HR之间的主效应均存在统计学意义，动作：F（2、58）=279.466，P=0.001，重复次数：F（5、145）=709.407，P<0.001。

2.1.3 不同重复次数三种抗自重动作能耗及心率的多重比较

确认存在显著性交互效应后，应进一步明晰重复次数变量的单独效应，Bonferroni多重比较结果显示，相同重复次数下，3个抗自重动作两两之间在能耗、心率指标上均存在显著性差异（各项P值确切数值详见表5，在此不一一赘述）。由X差值可见，3个抗自重动作在6种重复次数下的能耗、心率对比，俯卧撑最高，深蹲次之，提踵最低。

2.2 慢速自重抗阻训练能耗模型的建构

2.2.1 各测量指标与运动能量消耗的关系

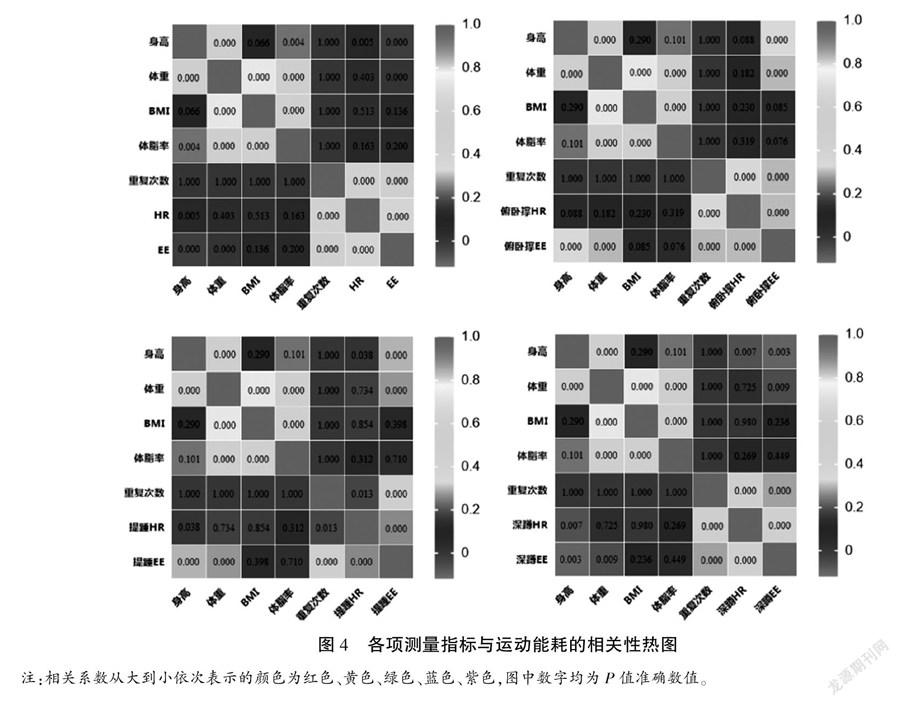
对各测量指标与运动总能耗、不同动作能耗进行相关性分析发现（见图4），身高、体重、心率、重复次数与运动总能耗（r=0.173，P<0.001;r=0.156，P<0.001;r=0.803，P<0.001;r=0.487，P<0.001）、俯卧撑能耗（r=0.325，P<0.001;r=0.299，P<0.001;r=0.828，P<0.001;r=0.831，P<0.001）、提踵能耗（r=0.295，P<0.001;r=0.269，P<0.001;r=0.258，P<0.001;r=0.512，P<0.001）及深蹲能耗（r=0.221，P=0.003;r=0.193，P=0.009;r=0.598，P<0.001;r=0.855，P<0.001）的線性相关关系显著。

BMI、体脂百分比与运动总能耗（P值分别为0.136、0.200）、俯卧撑能耗（P值分别为0.085、0.076）、提踵能耗（P值分别为0.398、0.710）及深蹲能耗（P值分别为0.236、0.449）均不存在相关关系，据图4结果，可建立能耗回归公式。

2.2.2 回归方程建立

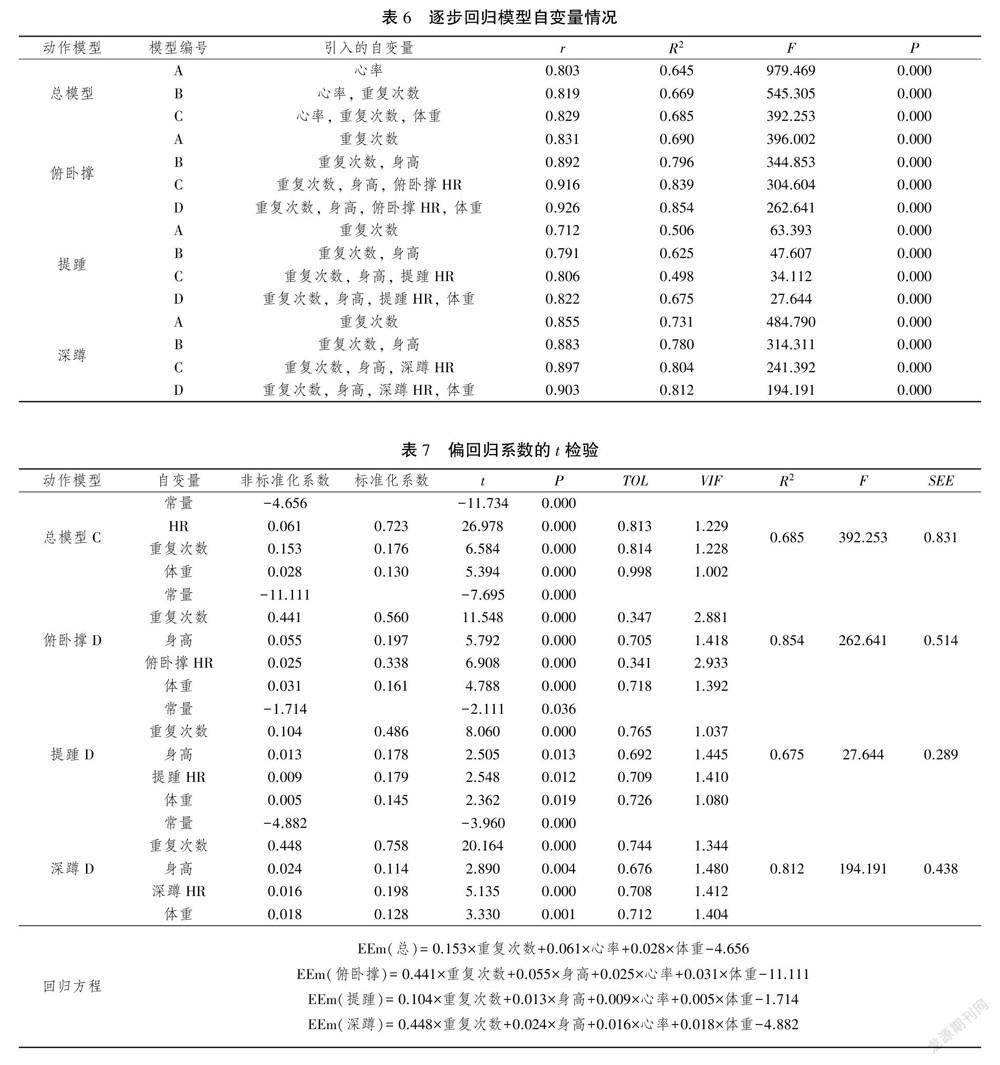
逐步多元回归的结果显示（见表6），总模型最终含有3个变量：心率、重复次数和体重，模型C的r=0.829，说明这3个变量与总能耗存在高度相关关系（P<0.001）;俯卧撑、提踵、深蹲模型均最终含有4个变量：重复次数、身高、心率和体重，其模型D的r分别为0.926、0.822、0.903，说明这4个变量与不同动作能耗均存在高度相关关系（P<0.001）;调整后的决策系数R2是衡量模型好坏的重要指标，4个模型调整后的R2决定系数分别为0.685、0.854、0.675、0.812，可见各模型效果较好。

表7给出了各模型自变量的偏回归系数估计值、标准化后的偏回归系数以及回归系数的显著性检验结果，结果显示总模型各自变量的容忍度（TOL）均大于0.813，方差膨胀因子（VIF）均小于1.229，俯卧撑模型各自变量的TOL均大于0.341，VIF均小于2.933;提踵模型各自变量TOL均大于0.692，VIF均小于1.445;深蹲模型各自变量TOL均大于0.676，VIF均小于1.480。因此4个模型各自变量间均不存在多元共线性问题。

总能耗、俯卧撑能耗、提踵能耗和深蹲能耗的线性回归方程见表8，各模型R2分别为0.685、0.854、0.675和0.812，SEE分别为0.831、0.514、0.289和0.438。心率、重复次数及体重3个自变量共可有效解释总能耗68.5的变异量，其中心率是对总能耗影响最大的变量;重复次数、身高、心率及体重4个自变量共可分别有效解释不同动作模型能耗的85.4、67.5和81.2的变异量，其中，重复次数是对不同动作能耗影响最大的变量，最先被引入模型;通过回归方程的方差分析对4个能耗方程进行检验，其F值分别为392.253、262.641、27.644和194.191，P值均小于0.001，可知回归方程是显著的，所建构的能耗方程具有统计学意义。

2.3 慢速自重抗阻训练能耗模型的准确性评估

2.3.1 各能耗模型预测值与实测值的相关性分析

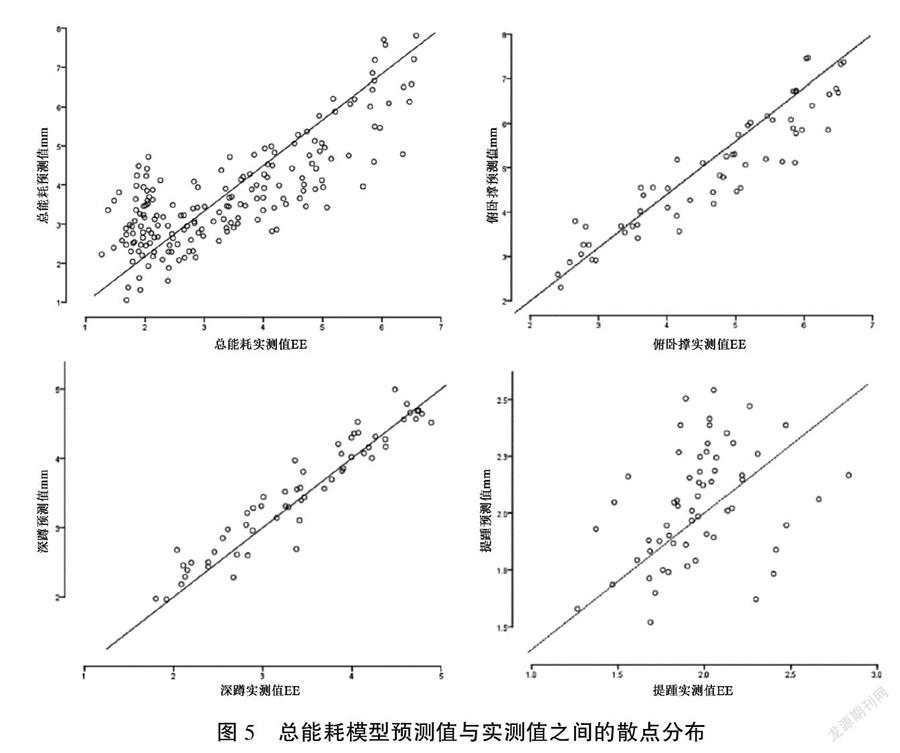
从预测值-实测值的散点图上看（见图5），深蹲模型的散点最为靠近参考线（y=x），具有较好的能耗预测效度;俯卧撑模型的散点普遍靠近参考线，但位于参考线以下的点居多;总模型和提踵模型的散点较为分散，预测误差明显高于其他2个模型。当总能耗实测值在1～3 kcal/min时，能耗预测值有较大波动，当实测值大于5 kcal/min后，点较为分散。

2.3.2 各能耗模型整体预测准确性比较

结合表8可知，总模型的能耗预测值与实测值存在中度相关关系（r=0.729，P<0.001），其RMSE、Bias、MAPE指标分别为0.75、0.19、0.29。俯卧撑、提踵、深蹲模型能耗预测值均与其实测值存在高度相关关系（r=0.929，P<0.001;r=896，P<0.001;r=0.911，P<0.001）。从3个不同动作模型的整体测量误差上看，深蹲模型在MAPE和Bias 2个指标上均低于提踵模型和俯卧撑模型（MAPE=0.08，Bias=0.01）;而在RMSE指标上，提踵<深蹲<俯卧撑，RMSE分别为0.24、0.28、0.46。

2.3.3 各能耗模型预测值与实测值的一致性检验

以验证组每个受试者的每项抗阻训练的6个重复次数为检验单元，使用Bland-Altman法对总能耗方程与间接测热法的一致性进行进一步的分析，图6中x轴代表各能耗预测值和实测值的均值，y轴代表预测值和实测值的差值，两条虚线为一致性界限表示差值95的置信区间，中间的实线为差值的均值。

本研究所计算的总模型、俯卧撑模型、提踵模型和深蹲模型的一致性限度区间分别为（-1.38，2.11）、（-0.70，1.28）、（-0.52，0.67）和（-0.70，0.75），差值的均线分别为0.36、0.29、0.07和0.02，一致性界限差值的绝对值分别3.49、1.98、1.19和1.45，在一致性区间之外的点分别9个、3个、6个和4个。从以上数据综合判断，4个模型的均值均接近0线，预测值与实测值95的残差均落在Bland-Altman散点图±1.96 SD区间内，表明4个模型对运动能耗均有较好的预测能力，俯卧撑模型和间接测热法的一致性水平最好。

3 分析与讨论

3.1 试验设计方案分析

传统抗阻训练主要是使用自由重量或高负荷负重器械来促使机体肌肉肥大[21]，然而，对于健身初学者、普通老年人以及临床人群来说，使用高负荷自由重量或器械训练需要较长时间的神经肌肉恢复[22]，且易造成运动损伤风险。故本研究侧重于利用人体自身重量进行的抗阻运动，满足抗阻训练的个体化、周期化和渐

进性原则，对于普通老年人群和健身初学者等来说是负重器械的可行替代品。传统速度抗阻训练定义为动作（离心和向心结合）完成时间小于4 s，慢速抗阻训练定义为向心或离心阶段持续2～6.5 s，总时间4～13 s，极慢速度抗阻训练定义为向心或离心动作大于等于10 s或总时间大于等于14 s。Lyons等人[23]的研究表明，以传统、慢速以及极慢速度的动作速度进行抗阻训练均能促进不同人群的肌力增长与肌肉肥大，且组间并无差异。另一项研究[24]比较传统速度与慢速两种不同训练节奏的单次站坐转换的能量消耗，发现运动速度为3 s上升、3 s下降的站坐转换的净能耗大约比运动速度1 s上升、1 s下降的高40。由此可以看出，慢速抗阻训练能够更好地促进神经支配肌肉的能力，并可能对缺乏训练经验的人群发展运动技能更有帮助。因此，本研究选取向心阶段3 s、离心阶段3 s的动作速度完成3个常见身体不同部位的抗自重动作（俯卧撑、提踵和深蹲）在6种不同重复次数下的测试。

3.2 慢速自重抗阻训练的能耗特征分析

本研究结果表明，俯卧撑的能耗最高，深蹲次之，提踵最低。该结果与国外相关研究结果基本一致，究其原因，产生此结果的主要原因将从动作目标肌肉、人体肌肉分布以及肌肉单次收缩幅度三方面来分析。从动作目标肌肉来看，俯卧撑主要是锻炼上肢、腰腹部位的肌肉训练动作，包括肱二头肌、肱三头肌及胸大肌等，尤其是胸肌，它是评估人体上肢力量素质的最常用方法;提踵动作的目标肌肉主要为腓肠肌;深蹲被认为是增强腿部、臀部力量和围度以及发展核心力量必不可少的练习。从人体肌肉分布来看，Janssen等人[25]对468名年龄在18～88岁的人进行的一项研究表明，大多数成年人下半身的肌肉质量和体积均大于上半身，男性下肢肌肉约占人体总重的54.9，上肢肌肉约占人体总重的42.9。从肌肉单次收缩幅度来看，前人有研究表明，人体在运动时上肢肌肉比下肢肌肉更加活跃，上肢肌肉在收缩频率、收缩次数以及工作时间方面均显著高于下肢肌肉[26]。而Janssen等人[25]在此基础之上发现，人体运动时上肢肌肉的收缩频率、收缩次数虽显著高于下肢肌肉，但下肢肌肉的收缩幅度大约是上肢肌肉收缩幅度的2～3倍，下肢肌肉单次收缩的幅度远大于上肢肌肉。由上可知，与深蹲、提踵相比，俯卧撑动作的覆盖肌群更多，故肌肉做功较多，其能量消耗最高。

3.3 各能耗模型的建构与效度分析

3.3.1 各模型的建构分析

身高、体重、BMI以及体脂百分比作为人体的身体形态指标，在运动能量消耗的相关研究中最为常用。本研究结果表明，身高、体重与运动总能耗及不同动作能耗的线性相关关系显著，对机体能量消耗有较大影响。

此外，运动过程的总能量消耗会随着重复次数的增加而线性增加[27]，本研究将不同自重抗阻运动的重复次数与能量消耗进行相关性分析，发现俯卧撑、深蹲动作的重复次数均与其能耗存在高度相关关系（r=0.813，P<0.001;r=0.855，P<0.001），提踵的重复次数与能耗存在中度相关关系（r=0.512，P<0.001），研究证明可选用重复次数建立不同动作的能耗回归公式。此结果与之前的研究基本一致，Nakagata等人[24]比较了两种不同训练节奏的单次站坐转换的能量消耗，研究发现两种训练节奏站坐转换的重复次数与能耗之间均存在高度相关关系（r =0.998～0.999，P<0.001）。另一项研究[28]探讨了两种不同跑步速度对180°转弯运动的能量消耗的影响，同样得出总耗氧量与重复转弯次数存在高度相关关系，会随重复转弯次数的增加呈线性增加 （4.3 km/h：r=0.973，5.4 km/h：r=0.996，P<0.001）。

心率是反映人体运动状态的重要指标，与能量消耗之间存在线性关系，心率测量是监测和评价能量消耗的常用方法之一。因此，运动时对心率的监测对于指导大众健身人群日常运动有着重要作用。本研究将心率与能量消耗进行相关性分析，发现俯卧撑的心率与能耗存在高度相关关系（r=0.828，P<0.001），深蹲的心率与能耗存在中度相关关系（r=0.598，P<0.001），故選用心率指标分别建立不同动作的能耗回归公式。此结果与之前的研究基本一致，李冲等人[29]研究两种常见力量负荷抗阻训练的能量消耗水平，结果表明心率在中等力量负荷（12 RM）、低力量负荷（25 RM）组合动作抗阻训练中均与能耗存在中度相关关系（r=0.538，P<0.001;r=0.732，P<0.001）。

本研究根据前人对机体能量消耗影响因素的研究，通过逐步多元回归分析最终以身高、体重、心率和重复次数作为自变量指标建构总能耗和不同动作能耗模型，通过回归方程的方差分析对各能耗方程进行检验，发现4个方程P值均小于0.001，能耗方程具有统计学意义。

3.3.2 各模型的预测准确性分析

在以往的研究中，不同学者使用不同的评价指标来衡量模型的预测能力，其中包括r、R2、RMSE 、BIAS和MAPE等指标。本研究通过逐步多元回归采用了上述评价指标，以不同受试者进行外部效度和准确性检验结果显示，总能耗模型R2为0.685、不同动作能耗模型R2分别为 0.854、0.675、0.812，且均显著相关。这与Lytle等人[12]的研究结果一致，该研究利用人体形态学变量及抗阻相关变量构建的最优模型能够较为合理地推算运动过程中的能量消耗，其总能耗模型R2为0.773、单项抗阻动作能耗模型R2范围为0.62～0.83。Benito等人[30]的研究结果与之相似，循环抗阻运动能耗预测方程女性R2为0.92，SEE=4.9;男性R2为0.79，SEE=7.7。另一项[31]研究表明，使用去脂体重、性别和腰部加速度计VM值所构建的能耗方程，共可有效解释抗阻运动能耗的73的变异量（R2=0.730）。值得注意的是，在研究中，总模型的RMSE、Bias、MAPE指标分别为0.75、0.19、0.29;不同动作能耗预测模型的RMSE指标分别为0.24、0.28、0.46。而在以往抗阻运动能耗预测模型的研究中并没有上述3个指标对模型准确性进行检验，后续研究需进一步展开讨论。

Bland-Altma图是指以图形的方式直观地反映两种测量结果的一致界限性，从而得出这两种测量方法是否具有一致性的结论，此方法可以运用于评估预测值与实测值的一致性，以此来检验模型的预测准确性[32]。本研究结果显示，总模型的一致性限度区间为（-1.38，2.11），不同动作能耗一致性限度区间分别为（-0.70，1.28）、（-0.52，0.67）和（-0.70，0.75），差值的均线分别为0.36、0.29、0.07和0.02，4个模型的均值均接近0线，且总模型和不同动作模型的大部分散点基本落在±1.96 SD 之间，证明各模型均具有良好的预测能力。而在以往的基于自重抗阻运动能耗预测模型的研究中并没有使用Bland-Altman法对模型准确性进行检验，因此未来研究应重视此方法的应用，使研究结果更加可靠。综上可知，已有的研究充分肯定了抗阻运动在健身与康复领域的价值，并已证明自重抗阻在力量训练中具有实际效用，且本研究推导的抗阻训练总能耗及不同动作能耗估算公式的预测值均是较为准确、可信的，为应用本研究推算公式计算健康男性自重抗阻训练能耗提供了可靠依据。但就目前而言缺乏对抗阻训练与能量消耗的剂量-效应关系进行系统探讨，也无法为本研究中的结果提供直接依据，故后续还需要更多研究进一步探讨其共变的因果关系。

3.4 本研究的局限

本研究中受试者均为40名年龄在19～25岁的健康男性，样本量较少，所建立的模型是否具有人群的局限性还需后续研究适当增加男女样本量加以探讨。在实验方案上，本研究中共选取3个抗自重动作，动作数量有限，未来可进一步丰富在实验室情景下的自重抗阻训练种类的相关研究，如引体向上、仰卧起坐等，并应在条件允许的情况下，构建多种能耗预测模型，进一步提高能耗模型的准确性。

4 结 论

（1）3个抗自重动作在6种重复次数下的能量消耗及心率对比，相同重复次数下，俯卧撑最高，深蹲次之，提踵最低。

（2）心率与总能耗存在高度相关关系，是对总能耗模型贡献最大的变量，重复次数与不同动作能量消耗均存在较高的相关关系，是预测能量消耗较佳的自变量。

（3）以身高、体重、心率等基本生理学参数和重复次数为自变量推导的能耗评价模型，能够较为准确地预测慢速自重抗阻训练的运动能耗，预测精度较高，可为自重抗阻运动能量消耗的科学监控提供实证参考。

参考文献：

[1]Hakkinen K， Kraemer WJ， Newton RU， et al. Changes in electromyographic activity， muscle fibre and force production characteristics during heavy resistance/power strength training in middle-aged and older men and women[J]. Acta Physiol Scand，2001 Jan;171（1）：51-62.

[2]Fleck S J. Cardiovascular adaptations to resistance training[J]. Medicine and science in sports and exercise， 1988， 20（5）：146-151.

[3]American College of Sports Medicine. American College of Sports Medicine position stand. Progression models in resistance training for healthy adults[J]. Med Sci Sports Exerc，2009，41（3）：687-708.

[4]于亮.慢速抗阻訓练：周期性增肌的新刺激模式[J].成都体育学院学报，2021，47（1）：40.

[5]朱琳，陈佩杰.能量消耗测量方法及其应用[J].中国运动医学杂志，2011，30（6）：577-582.

[6]Wilmore J H， Parr R B， Ward P， et al. Energy cost of circuit weight training[J]. Medicine and science in sports， 1978， 10（2）： 75-78.

[7]Gore C J， Withers R T. Effect of exercise intensity and duration on postexercise metabolism[J]. Journal of applied Physiology， 1990， 68（6）： 2362-2368.

[8]Bahr R， Ingnes I， Vaage O， et al. Effect of duration of exercise on excess postexercise O2 consumption[J]. Journal of Applied Physiology， 1987， 62（2）：485-490.

[9]Bahr R， Sejersted O M. Effect of feeding and fasting on excess postexercise oxygen consumption[J]. Journal of Applied Physiology， 1991， 71（6）：2088-2093.

[10]Short K R， Sedlock D A. Excess postexercise oxygen consumption and recovery rate in trained and untrained subjects[J]. Journal of applied physiology， 1997， 83（1）：153-159.

[11]Robergs R A， Gordon T， Reynolds J， et al. Energy expenditure during bench press and squat exercises[J]. Journal of strength and conditioning research， 2007， 21（1）：123.

[12]Lytle JR， Kravits DM， Martin SE， Green JS， Crouse SF， Lambert BS. Predicting Energy Expenditure of an Acute Resistance Exercise Bout in Men and Women. Med Sci Sports Exerc[J]. 2019，51（7）：1532-1537.

[13]Duffield R， Dawson B， Pinnington H C， et al. Accuracy and reliability of a Cosmed K4b2 portable gas analysis system[J]. Journal of Science and Medicine in Sport， 2004， 7（1）：11-22.

[14]Ledermann J， Harter P， Gourley C， et al. Olaparib maintenance therapy in platinum-sensitive relapsed ovarian cancer[J]. New England Journal of Medicine， 2012， 366（15）：1382-1392.

[15]鄧树勋，王建，乔德才，等.运动生理学[M].北京：高等教育出版社， 2009.

[16]Nakagata T， Naito H， Yamada Y. Metabolic equivalents of body weight resistance training with slow movement：Implications for exercise prescription and health promotion[J]. J Exerc Physiol Online ，2018，21（5）：29-38.

[17]田兴辰. 标准俯卧撑与不稳定俯卧撑的动作分析[D].上海：上海体育学院，2016.

[18]陈晨. 躯干位置对自重深蹲运动中下肢生物力学的影响研究[D].上海：上海体育学院，2019.

[19]Chandler T J， Stone M H. The squat exercise in athletic conditioning：A position statement and review of the literature[J]. Chiropractic Sports Medicine， 1992（6）：105.

[20]Weir J B V. New methods for calculating metabolic rate with special reference to protein metabolism[J]. The Journal of physiology， 1949， 109（1-2）：1-9.

[21]American College of Sports Medicine. American College of Sports Medicine position stand. Progression models in resistance training for healthy adults[J]. Medicine and science in sports and exercise， 2009， 41（3）：687-708.

[22]Fragala M S， Cadore E L， Dorgo S， et al. Resistance training for older adults：position statement from the national strength and conditioning association[J]. The Journal of Strength & Conditioning Research， 2019， 33（8）.

[23]Lyons A， Bagley J. Can Resistance Training at Slow Versus Traditional Repetition Speeds Induce Comparable Hypertrophic and Strength Gains？[J]. Strength and Conditioning Journal， 2020， 42（5）：48-56.

[24]Nakagata T， Yamada Y， Hatamoto Y， et al. Energy expenditure of a single sit-to-stand movement with slow versus normal speed using the different frequency accumulation method[J]. Medicina， 2019， 55（3）：77.

[25]Janssen I， Heymsfield S B， Wang Z M， et al. Skeletal muscle mass and distribution in 468 men and women aged 18–88 yr[J]. Journal of applied physiology， 2000，89（1）：81-88.

[26]Monster A W， Chan H， O′Connor D. Activity patterns of human skeletal muscles：relation to muscle fiber type composition[J]. Science， 1978， 200（4339）：314-317.

[27]Hatamoto Y， Yamada Y， Higaki Y， et al. A novel approach for measuring energy expenditure of a single sit-to-stand movement[J]. European journal of applied physiology， 2016， 116（5）：997-1004.

[28]Hatamoto Y， Yamada Y， Fujii T， et al. A novel method for calculating the energy cost of turning during running[J]. Open access journal of sports medicine， 2013（4）：117.

[29]李沖，史曙生.健康青年男性两种力量负荷抗阻训练能量消耗的推算[J].中国运动医学杂志，2019，38（5）：364-371.

[30]Benito Peinado P J， lvarez Sánchez M， Díaz Molina V， et al. Aerobic energy expenditure and intensity prediction during a specific circuit weight training：A pilot study[J]. 2010，5（2）：134-135.

[31]Puyau M R， Adolph A L， Vohra F A， et al. Prediction of activity energy expenditure using accelerometers in children[J]. Medicine & Science in Sports & Exercise， 2004， 36（9）：1625-1631.

[32]陈庆果，刘耀天，谭雅兮，等.腕部加速度计中不同类型能耗预测模型的建构与评估[J].首都体育学院学报，2019，31（3）：261-271.

收稿日期：2021-06-30

作者简介：杨丽君（1997- ），女，四川遂宁人，在读硕士研究生，研究方向体力活动测量与评价。

通讯作者：陈庆果（1981- ），男，博士，教授，研究方向体力活动测量与评价。

作者单位：四川师范大学体育学院，四川 成都 610101