一种轴对称变几何进气道气动设计及性能分析*
2021-02-17宁啸天辜天来田亚洲刘甫州袁化成
宁啸天,辜天来,田亚洲,刘甫州,袁化成
(1.南京航空航天大学 能源与动力学院, 南京 210016;2.中国运载火箭技术研究院 研究发展部, 北京 100076)
0 引言
大气层内飞行时,吸气式发动机能够以空气为氧化剂,具有相对较高的比冲,是一种较为理想的动力装置[1],采用了吸气式推进的飞行器往往具有较低的成本[2],且易于重复使用。进气道是吸气式发动机的重要组成部分,对整个推进系统的性能有重要影响,制约着整个推进系统功能的发挥和性能的提高。轴对称布局形式的进气道外形上与涡轮发动机更容易匹配,也易与一些飞行器的气动外形融合,如便于导弹的携带和箱式发射[3]。因此,此类布局形式的进气道成为吸气式动力装置的重要选择之一,受到了国内外学者的关注,对其气动设计与气动特性的研究具有重要意义。
在宽域飞行马赫数的设计要求下,定几何设计进气道在非设计点马赫数下存在流量需求难以匹配以及内部流动易分离、性能较差的问题[4],这使得变几何技术应运而生。通过引入各种变几何机构,不仅能够调整进气道捕获流量以适应宽马赫数工作范围要求下的发动机需求流量变化,也能够调整进气道型面以改善进气道在不同工况下的内部流动,提高进气道的性能,上述优点使得变几何设计技术成为解决宽域工作进气道气动设计问题的重要方案之一。
国外对轴对称变几何进气道的研究起步较早,研究方案较多,形成了一些具有代表性的方案:美国SR-71高空高速侦察机采用了可移动中心锥式轴对称进气道设计[5],在不同的飞行马赫数下,通过前后移动中心锥,改变唇口与外压段激波的相对位置以调整捕获流量,同时改变内收缩段的收缩比以调整进气道的通流能力;JAMES F Connors等[6]提出了在中心锥设置槽道的变几何方案,低马赫数下中心锥前移,槽道开启,增大了喉道面积,提高了进气道起动能力;YUSUKE Maru等[7]设计了一种多级圆盘组合而成的中心锥,在较低的飞行马赫数下,各级圆盘分别前移,圆盘间形成的凹腔被涡流填满,从而在圆盘间形成气动连接面,在不过分破坏外压缩流场的条件下,使得进气道的捕获流量得到了可控调节。
近年来,国内对于轴对称进气道变几何设计的研究也逐渐增多[8-15],南京航空航天大学的王亚岗等[16]研究了移动中心锥的变几何方案,给出了喉道面积可变的设计方法,并研究了抽吸对于进气道整体性能的影响。滕健等[17]提出了类似多圆盘设计的变几何方案,实现了宽速域马赫数范围内保证进气道流量系数的目的。苗海丰等[18]研究了一种简单易实现的变几何方法,通过旋转进气道第一级压缩锥改变进气道外压段激波的角度和位置,有效地改善了进气道的攻角特性。
总体来说,移动中心锥变几何思路在轴对称超声速进气道的变几何设计中采用较多,相对较为成熟,其气动本质是改变了外压段激波与唇口的相对位置,从而达到在不同飞行马赫数下调整捕获流量的目的。然而,移动中心锥方案通常需要将作动机构置于进气道内部,结构设计上难度较高,而本文研究借鉴其气动设计思路,拟通过平移唇罩的方式实现与移动中心锥相似的改变外压段激波与唇口相对位置,进而达到调整进气道不同状态下捕获流量的目的,此时唇罩的平移运动机构可置于进气道外部,大大降低了变几何方案结构实现难度。
1 总体要求及设计思路
1.1 总体要求
本文拟研究的轴对称进气道最大工作马赫数为4,其设计约束指标要求在Ma=2~4范围内的流量与发动机需求匹配,具体的流量系数需求如表1 所示。
1.2 设计思路
进气道的设计马赫数为4,因此进气道的压缩段选择混压式设计。进气道的各个功能结构如图 1 所示,可以看到,外唇罩在进气道喉道位置的部分可以设计成圆柱形,便于引入滑套结构设计以实现几何可调。因此,在结构上实现唇口位置可调的方案是较为切实可行的。

表1 流量系数设计要求

图1 混压式进气道结构示意图
图 2 给出了本文所研究进气道的总体设计框架。根据进气道功能分区,压缩段的设计参数包括外压缩面设计和内压缩通道设计,扩张段的设计包括面积和中心线的变化规律,以及环形段长度占整个扩压段的比例。与定几何轴对称进气道设计有所不同的是,由于唇口位置可调,因此不同来流马赫数下的流量系数均能够达到目标,但由于喉道面积固定,设计内压缩通道时,必须首先考虑喉道高度能否保证低马赫数下的起动性能。
结合轴对称进气道的主要设计参数,同时为了加入唇罩可调的变几何方案,确定气动设计的流程是:根据设计马赫数外压缩激波封口的要求,先进行外压段设计,确定设计马赫数下唇口位置,再根据流量需求确定变几何规律,确定唇口的位置。外压段设计完成,再选取唇口位置流场参数相对较好的外压段进行内压段的匹配,再对该组合进行唇口内角的规律研究,以来流马赫数为Ma=2时设计喉道位置,以保证进气道起动性要求。压缩段确定后,由于进气道总长固定,扩张段长度也被确定,对扩压段设计进行研究,分别对比面积变化规律、中心线变化规律以及环形段比例的影响。最后,得到完整的唇罩可动式轴对称超声速变几何进气道气动设计与变几何规律。
2 数值计算方法
采用经过课题组验证的数值计算方法[16],使用成熟的流体仿真软件Fluent进行计算,湍流模型为标准k-ε模型,对类似工作范围的轴对称进气道流场仿真与试验结果对比如图 3 所示,数值方法与试验结果较符合。
图 4 展示了进气道其中一个状态点的计算域网格划分,可看到压缩面转折处和壁面均进行了加密处理。图 5 给出了计算域的边界条件设置。
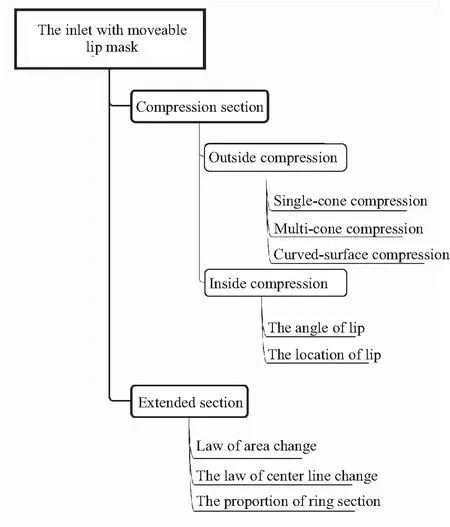
图2 设计框架
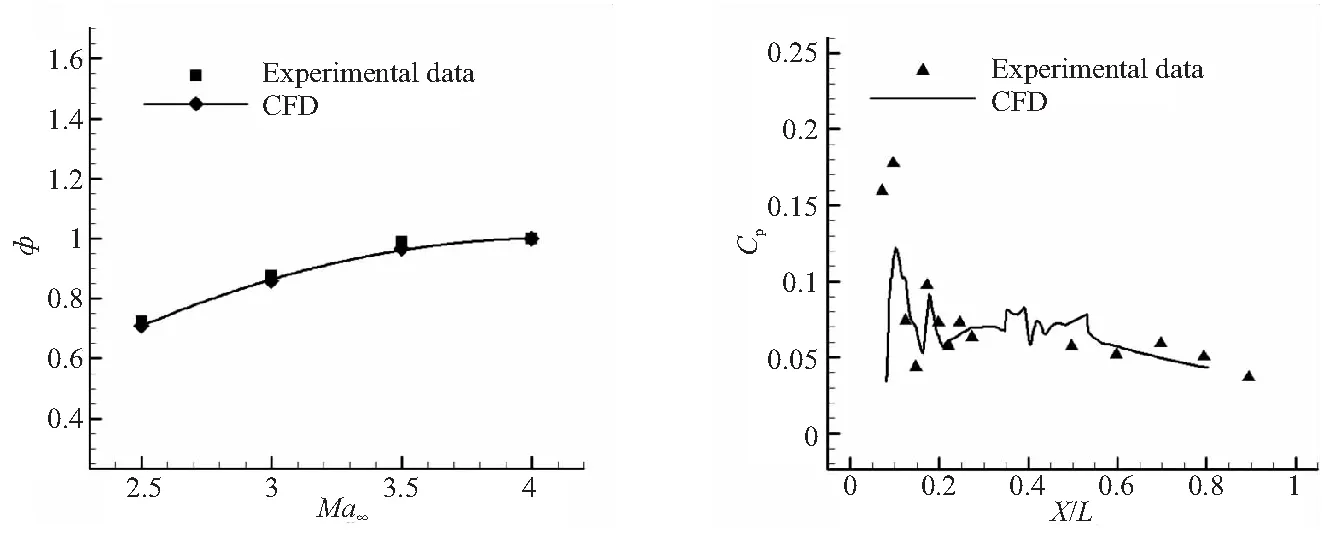
(a)Mass-flow coefficient (b)Wall pressure distribution
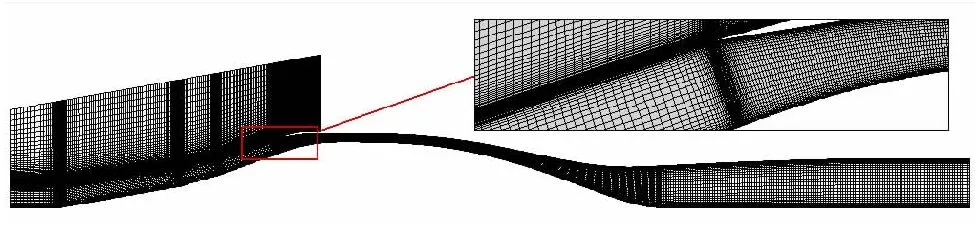
图4 网格划分
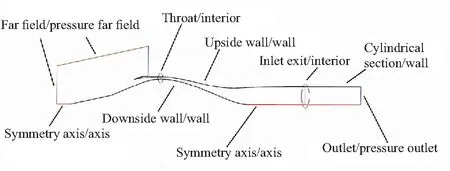
图5 计算域与边界条件
3 唇罩可动式轴对称进气道气动设计
3.1 外压段波系配置对进气道气动特性的影响
外压缩段位于进气道的最前端,是进气道的重要组成部分之一。对于本文拟采用的变几何设计方案而言,外压段波系配置不仅影响到下游内收缩段与扩压段的设计,同时也直接关系到进气道不同来流马赫数下的流量捕获特性,以及几何调节规律。外压缩方案中,单锥压缩方案结构简单,相同压缩角时长度最短,多锥压缩方案长度较长,但相同压缩比时,总压恢复系数更高,截短的曲面压缩方案则能在长度与性能间有所平衡。为此,从几何总转折角度相同以及气动压缩效果相近两个角度开展外压段方案设计,对比分析不同方案下的气动性能以及几何调节移动距离。
3.1.1 相同外压段总转折角下进气道性能对比分析
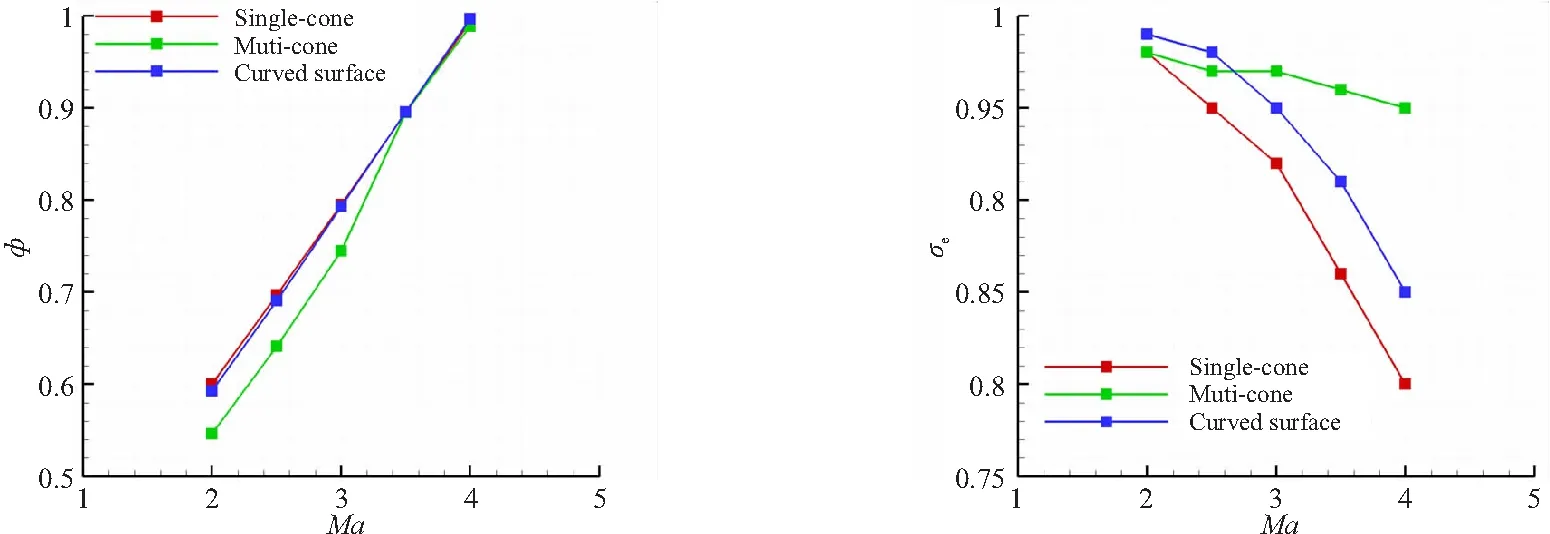
选择Ma=4为进气道激波封口马赫数,借鉴课题组前期研究积累[16],取外压缩段总转折角为20°。在相同的外压段转折角度下,3种不同波系配置下的外压段气动方案设计。其中,三级压缩方案是参考Oswaititsch最佳波系理论获取,三级半锥角分别为10°、16°、20°。曲面压缩采用流线追踪方法生成,型面由课题组曲面压缩设计程序给出,初始压缩锥半角为10°。图 6 给出了上述3种方案下进气道性能参数随来流马赫数的变化曲线,其中唇口位移参数以设计点Ma=4时的唇口位置为初始零点,随着来流马赫数降低唇口不断向来流方向前移,以满足进气道流量捕获特性与设计指标的一致性。
(a)Mass-flow coefficient of fixed geometry design (b)Total pressure recovery coefficient of the lip section

(c)Mach number of the lip section (d)Static pressure ratio of the lip section

(e)Moving distance of lip/Diameter of lip
从图 6 可看出,随着来流马赫数的增加,3种方案下进气道的流量系数、唇口截面的静压比和马赫数均逐渐增大,而总压恢复系数则逐渐减小。在总外压段转折角相同的条件下,在定几何设计时,三级锥压缩方案的流量捕获能力低于单锥压缩与曲面压缩,但总体来看,三级锥压缩的总压恢复系数最高,曲面压缩次之,单锥压缩最低。表2 给出了Ma=4状态下不同外压缩方案的性能对比。由于曲面压缩初始锥半角为10°,而总转折角为20°,因此相对较短的曲面压缩段使得曲面设计相比直单锥设计其总压恢复系数提高有限。3种压缩方案在唇口处马赫数、静压比相近,三级锥压缩略高于单锥与曲面压缩。引入唇口可动的变几何方案时,在满足不同来流马赫数的流量需求条件下,三级锥压缩唇罩的移动距离最短,这将使得变几何设计的结构实现难度降低,而单锥与曲面压缩唇罩移动距离较为相近。综合气动性能及几何调节移动距离,就本文的进气道流量捕获特性目标而言,三级锥压缩方案综合性能相对较优。

表2 Ma=4状态相同总转折角外压缩方案性能对比
3.1.2 唇口马赫数相同时进气道性能对比分析
取3种外压缩方案在设计点的唇口马赫数Mai在3附近作为对比的条件,此时单级锥外压段总转折角为19.2°,三级锥方案转折角度为20°,曲面压缩方案总转折角度为19.4°。
图 7 给出了上述3种方案下进气道性能参数随来流马赫数的变化曲线。从图 7 可看出,随着来流马赫数的增加,3种方案下进气道的流量系数、唇口截面的静压比和马赫数均逐渐增大,而总压恢复系数则逐渐减小。在设计点唇口马赫数均为2.94的条件下,在定几何设计时,三级锥压缩方案的流量捕获能力低于单锥压缩与曲面压缩,但总体来看,三级锥压缩的总压恢复系数最高,曲面压缩次之,单锥压缩最低, 表 3 给出了Ma=4状态下不同外压缩方案的性能对比,3种压缩方案在唇口处马赫数、静压比相近,三级锥压缩略高于单锥与曲面压缩。

(a)Mass-flow coefficient of fixed geometry design (b)Total pressure recovery coefficient of the lip section

(c)Mach numer of the lip section (d)Static pressure ratio of the lip section

(e)Moving distance of lip / Diameter of lip
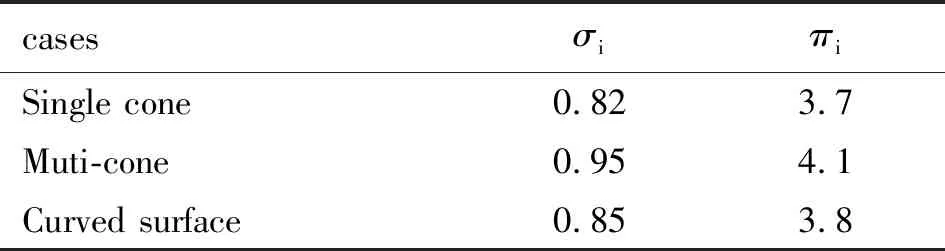
表3 Ma=4状态相同唇口马赫数外压缩方案性能对比
引入唇口可动的变几何方案时,在满足不同来流马赫数的流量需求条件下,三级锥压缩唇罩的移动距离最短。总体来看,三级锥压缩方案综合性能更好。这与保证总转折角相同时,不同外压缩段设计得到的流场参数随来流马赫数变化的规律基本一致。
3.2 内压段型面设计对进气道气动特性的影响
内压段设计对进气道气动性能具有重要影响,其主要设计参数包括内收缩比及影响内压段波系结构的唇罩内角度及沿程几何面积分布规律等。其中,内收缩比在保证进气道低马赫数起动的条件下取尽可能更大,这使得喉道位置基本确定,而喉道与外压段取合适的倒圆过渡连接。因此,就本文所研究进气道而言,内压段通道型面的主要设计参数为唇口内角取值。在进气道外压段和扩压段设计相同的条件下,本文对比了不同唇口内角所得到的内压段设计对进气道气动特性的影响。
唇口内角的设计,会影响内收缩段激波系分布以及拐点流场分离的大小,从而影响喉道流场参数,进而对进气道性能产生影响。为了保证唇罩平移的变几何方案在工程实现上无矛盾,需要唇罩在喉道附近有足够的圆柱段长度来做平移运动。因此,选择唇口内角的取值分别为9°、10°、11°、12°、13°。图 8 给出了随来流马赫数变化不同唇口内角进气道的性能变化曲线。
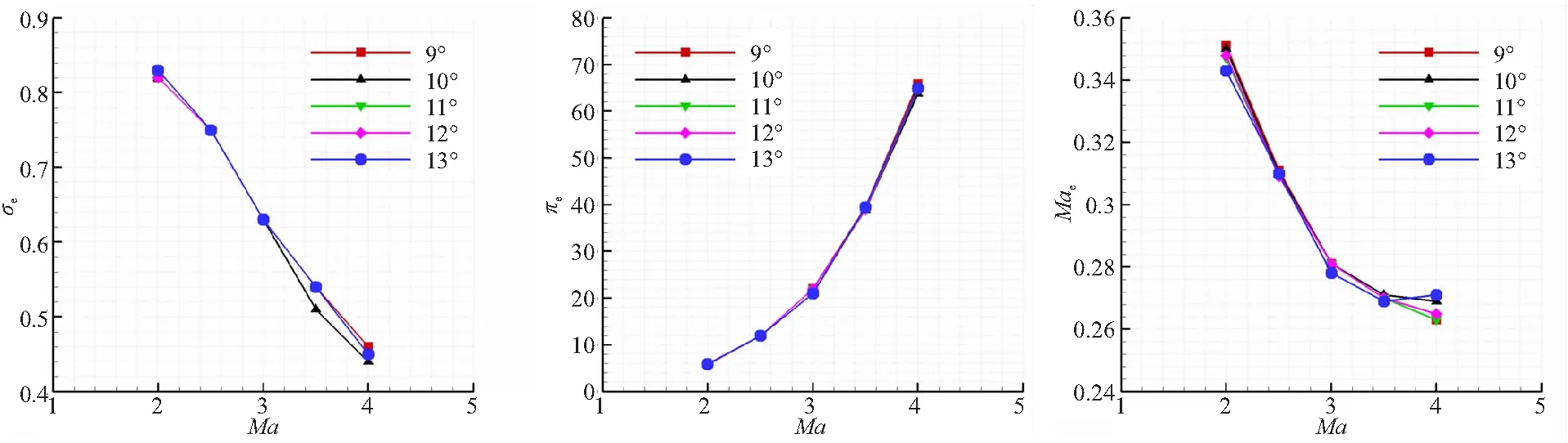
(a)Total pressure recovery coefficient (b)Static pressure ratio of the (c)Mach number of
从图 8 可看出,随着来流马赫数的增大,5种不同唇口内角设计的进气道,其出口总压恢复系数、马赫数均逐渐减小,而出口静压比则逐渐增大。表 4 给出了采用不同大小唇口内角的进气道性能对比,不同唇罩内角的进气道在出口的总压恢复系数和静压比相近,总体来看,9°方案均略高于其他方案。在设计点状态下, 10°与13°方案出口马赫数相对较高。总体来看,9°唇口内角方案的综合性能相对较好。
3.3 扩压段设计对进气道气动特性的影响分析
扩压段使得气流经过喉道激波串后的气流进一步减速增压,良好的扩压段设计能够保证更高的静压升与更低的粘性损失。扩压段的设计参数包括扩压段中心线变化规律、面积变化规律以及环形段占扩压器总长的比例。本文分别对比了不同的中心线、面积变化规律和环形段比例时,进气道在不同来流马赫数下的气动性能。其中,各个方案在压缩段设计相同的条件下进行对比。

表4 Ma=4状态不同唇口内角方案性能对比
3.3.1 中心线变化规律对进气道气动特性的影响
图 9 给出了不同的中心线变化规律下,进气道气动性能参数随来流马赫数的变化曲线。可见,随着来流马赫数的增大,不同中心线变化规律的进气道,其出口总压恢复系数、马赫数均逐渐减小,而出口静压比则逐渐增大。

(a)Total pressure recovery coefficient (b)Static pressure ratio of the (c)Mach number of
表 5 为采用不同中心线变化规律的进气道性能对比,3种中心线变化规律下,进气道出口的总压恢复系数、静压比以及马赫数均比较相近。采用缓急相当的变化规律的进气道总压恢复系数略高于其他方案,且出口马赫数略低于其他方案,总体来看,缓急相当的中心线变化规律较优。
3.3.2 面积变化规律对进气道气动特性的影响
图 10 为不同面积变化规律的进气道气动性能参数随来流马赫数的变化曲线。可见,随着来流马赫数的增大,不同面积变化规律的进气道,其出口总压恢复系数、马赫数均逐渐减小,而出口静压比则逐渐增大。
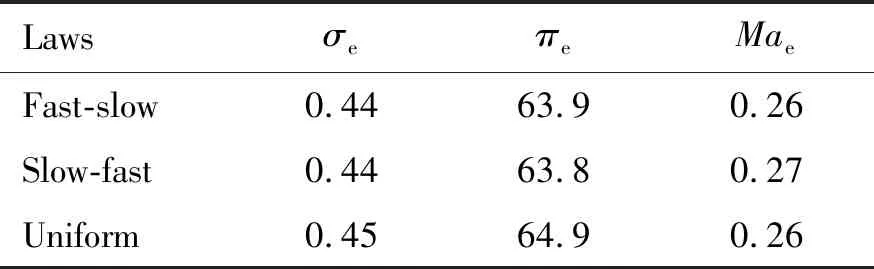
表5 Ma=4状态不同中心线规律性能对比

(a)Total pressure recovery coefficient (b)Static pressure ratio of the (c)Mach number of
表 6 给出了采用不同面积变化规律的进气道性能对比,3种面积变化规律下,进气道出口的总压恢复系数、静压比以及马赫数均比较相近。
采用先急后缓变化规律的进气道在低来流马赫数下出口马赫数更低,但在设计马赫数时较高,总体来看,缓急相当的面积变化规律较优。
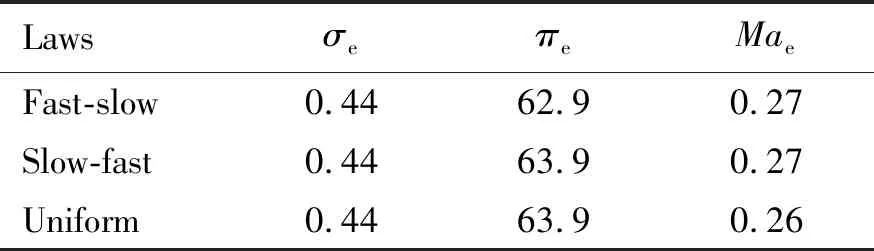
表6 Ma=4状态不同面积变化规律性能对比
3.3.3 环形段比例对变几何进气道气动特性的影响
中心锥与唇罩在喉道后形成的通道长度(即扩压器环形段长度)占扩压段总长度的比例,影响到气流在扩压器中粘性损失与流动特性。本文研究了环形段长度比例分别为0.4、0.5、0.6以及0.7时,进气道的性能变化规律。图 11 给出了不同环形段比例进气道的气动性能参数随来流马赫数的变化曲线。从图 11 可以看出,随着来流马赫数的增大,不同环形段比例的进气道,其出口总压恢复系数、马赫数均逐渐减小,而出口静压比则逐渐增大。表 7 给出了采用不同环形段比例的进气道性能对比,4种环形段比例的进气道,其出口的总压恢复系数、静压比均比较相近,但环形段比例为0.7时,进气道的出口马赫数总体低于其他方案。总体来看,比例为0.7的方案性能较优。

(a)Total pressure recovery coefficient (b)Static pressure ratio of (c)Mach number of the
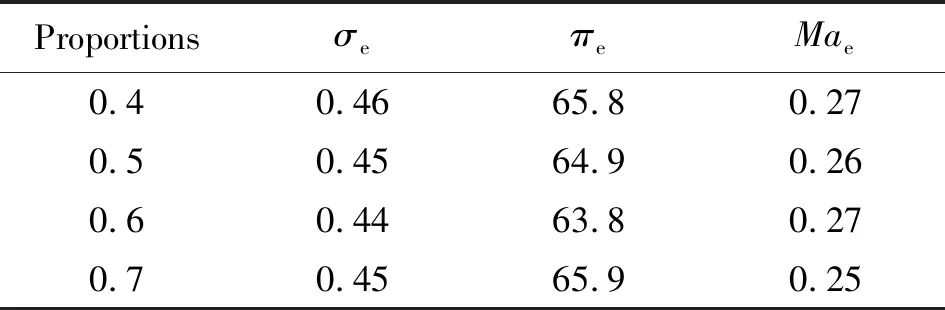
表7 Ma=4状态不同环形段比例的性能对比
4 唇口可动进气道气动设计方案及性能分析
通过前文对进气道典型设计参数的对比分析,选择最终的二维设计方案为三级锥压缩(第一级锥半角为10°,第二级锥半角为16°,第三级锥半角为20°)、9°唇口内角、缓急相当的面积变化规律、缓急相当的中心线变化规律,以及环形段占扩压段总长比例为0.7。图 12 展示了来流马赫数为4时最终的二维设计模型。进气道总长L=5000 mm,扩压段总长Ls=3260 mm。唇罩前缘直径Di=423 mm。

图12 进气道最终设计(Ma0=4)
图 13 给出了不同来流马赫数下,最终的变几何进气道设计方案数值模拟得到的流场,以及唇罩随来流马赫数变化的位移规律。
图 14 给出了不同来流马赫数下,最终二维设计方案的流量系数指标与需求的对比,以及进气道出口的总压恢复系数和马赫数变化。可以看到,根据本文设计方法所得到的唇罩可动式轴对称进气道能够达到预期设计目标,在设计点Ma=4状态时,其出口总压恢复系数为0.45。
5 结论
本文以不同来流马赫数下的流量系数为目标,对Ma=4级唇罩可移动型轴对称可调进气道设计开展了研究,由于平移唇罩方案在变几何过程中仅改变内压段通道,设计上与外压段、扩压段型面没有直接耦合,因此采用了对进气道分段设计、再组合每段最优方案的方法,达到了预期的设计目标,设计流程清晰,对此类进气道的设计方法上有一定借鉴意义,而在细节上对进气道各分段设计仍有进一步的研究空间。例如,对曲面压缩方法的优化研究。
(1)兼顾几何移动距离和气动性能综合考虑,采用三级锥压缩的外压段方案优于单级压缩锥方案和曲面压缩锥方案;
(2)内压缩段唇罩内角对进气道内压段流动和进气道性能,就本文研究的进气道而言,9°唇口内角设计时,进气道的性能相对较优;
(3)就本文研究的可调进气道而言,采用缓急相当的中心线、面积变化规律和环形段比例为0.7时的扩张段设计,在相近的总压恢复系数与静压比下,可以获得更低的进气道出口马赫数;
(4)三级锥设计获得了满足目标流量系数要求的轴对称可调进气道方案,给出了几何调节规律,数值模拟结果显示:不同来流马赫数下,可调进气道的流量系数与设计目标一致,Ma=4和Ma=2时,进气道的总压恢复系数为0.45和0.82。

(a)Ma=2.0 (b)Ma=2.5 (c)Ma=3.0
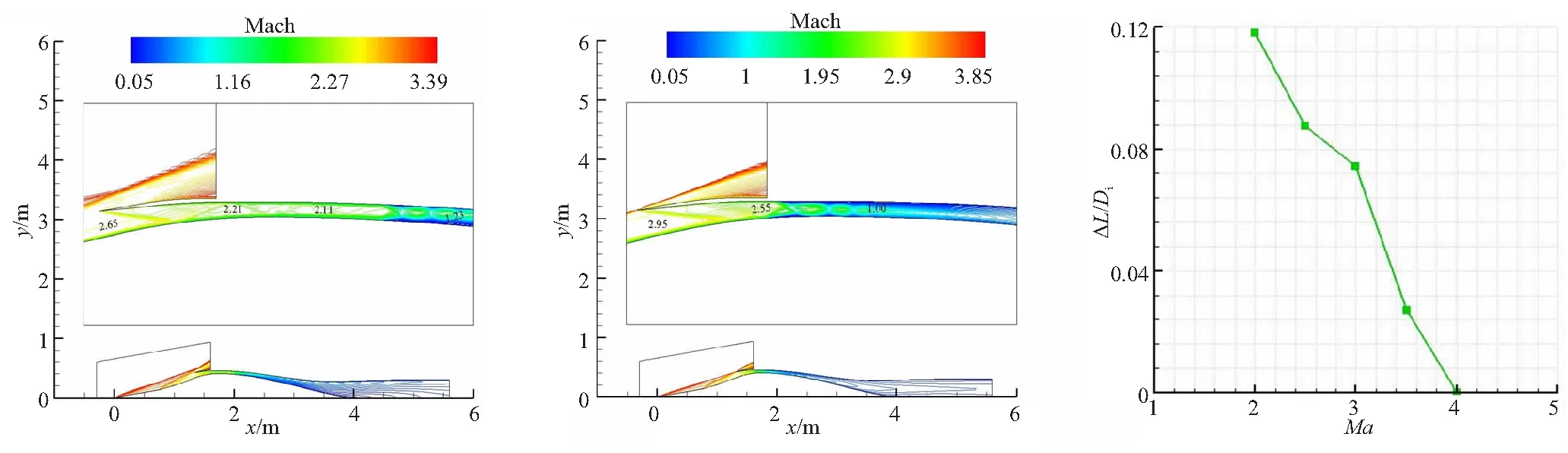
(d)Ma=3.5 (e)Ma=4.0 (f)Moving distance of lip/diameter of lip

(a)Comparison of mass-flow coeffication (b)Total pressure recovery coefficient and
