改进G1-RS-UMT模型在某配水工程围岩稳定预测中的应用

靳春玲， 党丹丹， 贡 力， 魏晓悦， 贺思乐

(1.兰州交通大学 土木工程学院， 甘肃 兰州 730070； 2. 国网甘肃省电力公司白银供电公司， 甘肃 白银730900)

1 研究背景

由于水工隧洞施工情况复杂，且开始呈现“长洞线、大洞径、隧洞群”的复杂特性，这使得水工隧洞围岩的稳定性难以得到保证，也增加了围岩支护方案设计和应力分析的难度[1-2]。因此，为预防支护结构不能稳固围岩，避免造成巨大的人力和财力损失，需要对围岩稳定性做出准确的预测[3]。

针对水工隧洞及地下工程围岩稳定性等级预测，李唱唱等[4]对深埋高应力地质条件下引水隧洞的围岩稳定性进行了研究；李一冬等[5]将基于Nguyen-Widrow初始化等算法改进的BP神经网络应用到围岩等级预测中，并筛选出了影响围岩稳定性的主导因素；Zhang等[6]构建了6个影响因子评价体系，基于距离判别分析理论建立了围岩稳定性等级分类模型；宫凤强等[7]根据突变级数理论对影响围岩稳定性的因素进行层次分解，并结合模糊数学理论得到了围岩稳定类别；Li等[8]选用6个影响因素作为贝叶斯判别分析法(Bayes discriminant analysis)的判别因子，用来确定围岩稳定性的类别；Luo等[9]通过对围岩机理的研究，运用Singh-Mitchell model模型对隧道运营前的围岩变形规律进行了分析和预测;王克忠等[10]基于围岩稳定支护结构的力学机理分析和数值模拟，提出了钢拱架复合支护体系可以保证引水洞室的稳定性。针对预测围岩稳定性的理论还有概率统计分析[11]、支持向量机[12]、突变级数法[7]、距离判别分析理论[13]等。上述研究均取得了一定效果，但存在对影响隧洞围岩稳定的因素考虑不全,评价指标数据处理不当和稳定性分级边界模糊的问题。

综上所述，本文选用能合理反映围岩各项特性的指标，建立了珠江三角洲水资源配置工程B4标段围岩稳定性预测体系，采用G1(G1-coefficient)[14]-改进RS(rough set)[15]对各影响指标进行主客观赋权，并引用博弈论理论(game theory)[16]运算组合权重，基于未确知测度理论(unascertained measurement theory, UMT)[17]构建了改进G1-RS-UMT模型，用以解决珠江三角洲水资源配置工程B4标段的输水隧洞围岩稳定性的预测问题。并依据预测结果进行了开挖及支护方案的设计，取得了理想的效果，本研究可为水工隧洞围岩稳定性等级预测提供一种新的探索方法。

2 水工隧洞围岩稳定性预测模型

水工隧洞围岩稳定预测模型的基础是利用“G1法-改进RS-博弈论法”对影响水工隧洞围岩稳定性的指标进行组合赋权，再将组合赋权的结果引入改进G1-RS-UMT模型中，预测出水工隧洞的围岩稳定性等级结果。

2.1 组合赋权

通过G1法计算评价指标主观权重，再由改进RS法得到指标客观权重，最后基于博弈论法将评价指标的主客观权重进行组合赋权。

2.1.1 G1法主观赋权 G1法是基于层次分析法改进后的一种方法，省去了矩阵一致性检验的步骤，同时计算过程也较为简便，其确定评价指标主观权重的计算步骤如下。

Step 1 根据重要度大小确定指标的顺序。对于指标集{x1,x2,…,xn}，x1为n项指标中最重要的一个指标，x2为次重要指标，对n项指标进行重要度排序可得到：x1>x2>…>xn。

Step 2 判断相邻指标间重要性大小ri，重要度量化见表1[18]。

表1 重要度量化表

Step 3 计算权重系数。

(1)

wi-1=wi·ri

(2)

式中：wn为第n项指标的权重。

2.1.2 改进RS法客观赋权 改进RS法是为了避免粗糙集理论计算重要度的结果出现“0”的情况，通过改进重要度计算方法[19]来提高结果的精确度，其确定评价指标客观权重的计算步骤如下。

(1)粗糙集理论。知识集S=(URVf)，其中U=(X1,X2,…,Xm)为对象集，称为论域；R=C∪D为属性集(若C与D分别为条件属性集与决策属性集，则C∩D=Ø；V=Ur∈R·Vr，Vr为属性，r∈R为值域；f：U×R→V为信息函数，∀r∈R，X∈U，f(x,r)∈Vr。在知识集S=(URVf)中，属性ai∈R在属性集R-{ai}的重要度定义见公式(3)。

(3)

属性ai的权重Wai计算见公式(4)。

(4)

(5)

式中：|Ri|为集合Ri中属性的个数。

(2)粗糙集的改进。属性c的重要度计算如公式(6)所示。

Sig′(c)=I(D|C-{c})-I(D|C)+

(6)

决策属性D(U| D={D1,D2,…,Dk})相对于条件属性集C(U| C={C1,C2, …,Cm})的条件熵见公式(7)。

(7)

属性c的客观权重计算见公式(8)。

(8)

2.1.3 博弈论组合赋权 G1法和改进RS法各有其优缺点，但究其根本两者有很强的互补性。基于博弈论理论将主客观权重进行线性组合，从而得到评价指标的综合权重，其计算步骤如下。

Step 1用w=(w1,w2,…,wn)表示各指标的权重集，构建主、客观权重任意线性组合式如公式(9)所示。

wj=t1αj+t2βj(j=1,2,…,n)

(9)

式中：t1，t2为线性组合系数;wj表示所有的权重向量集；αj和βj为第j种赋权法确定的权重向量。

Step 2 根据博弈论思想构建优化模型如公式(10)所示。

(10)

式中：W1为主观权重;W2为客观权重。

Step 3 利用矩阵的微分性质，求出优化模型的最优解。

(11)

Step 4 由式(11)计算可得t1和t2，然后由公式(12)进行归一化处理。

(12)

Step 5 计算评价指标的最优组合权重W*。

(13)

2.2 改进G1-RS-UMT预测模型

设待评价的水工隧洞有n个洞段，即待评价洞段空间R={R1,R2,…,Rn}。设第Ri洞段(i=1,2,…,n)有m个评价指标，形成指标空间I={I1,I2,…,Im}，则有第Ri洞段第j个指标的测量值Xij。设评价指标有q个预测等级，则等级空间A= {A1,A2,…,Aq}，其中At(t=1,2,…,q)表示第t级，并称{A1,A2,…,Aq}为A上的有序分割类。

Step 1 计算单指标未确知测度。建立指标的未确知测度函数μ(Xij∈At)，将测量值Xij代入求得单指标测度评价矩阵μijt如公式(14)所示。

本研究严格按照Delphi专家咨询法,构建了一套科学、合理的康复专科护士核心能力评价指标体系，包括8个一级指标、21个二级指标和66个三级指标。专家对各个指标的意见具有高度的一致性，可信度高，同时具有一定的科学性和权威性，并且各指标的权重设置合理，为康复专科护士培养、资质认证和能力评价提供参考依据。本研究并未对指标内在品质进行研究，因此，对康复专科护士核心能力评价指标的信效度检验，将是下一步研究的重点内容。

(14)

Step 2 计算多指标综合测度矩阵

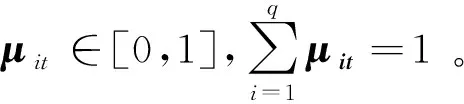
(15)

(i=1,2,…,n;t=1,2,…，q)

由公式(16)计算得到多指标综合测度矩阵。

(16)

Step 3 置信度识别准则。选取置信度λ=0.5(0.5≤λ≤1)，若λ满足公式(16)，则可以确定第Ri洞段属于第ta个预测等级Ata。根据预测等级可以得到每个洞段围岩的稳定性状态，进而设计相关开挖及支护方案。

(17)

3 实例应用

珠江三角洲水资源配置工程位于广东省东莞市沙田镇和厚街镇，主要为珠江口东岸三角洲平原地貌，东部沙溪水库附近局部分布丘陵，地表高程多为0～18 m。以珠江三角洲水资源配置工程的土建施工B4标段为例，其主要为8.453 km单线输水隧洞，将改进G1-RS-UMT模型应用于此水工隧洞围岩的稳定性预测中。

3.1 围岩稳定性预测指标体系

水工隧洞围岩的稳定是由多种因素之间的非线性关系所决定的，影响因素主要有内在因素和工程施工因素[20]，对其进行等级预测是一个非常复杂的过程。基于此，分析珠江三角洲水资源配置工程中影响B4标段输水隧洞围岩稳定性的各类因素，主要有：①岩体坚硬程度，岩体坚硬程度作为影响围岩稳定的首要因素，结合所处地质环境能极大程度上反映围岩岩体稳定性[21]；②岩体完整度，岩体完整度所反映的岩体结构状态是决定围岩岩体稳定的关键；③其他因素，除岩体本身以外，地下水、初始地应力等也能对水工隧洞围岩稳定性产生影响。

结合以上对影响围岩稳定性因素的分析，按照《水利水电工程地质勘察规范》(GB 50487—2008)、《岩土工程勘察规范》(GB 50021—2001)、《水工隧洞设计规范》(SL279—2016)、《工程岩体分级标准》(GB/T 50218—2014)、Q值法、BQ(basic quality)法和RMR(rock mass rating)法[22]，最终选取了10个具有代表性的指标，并将各指标的具体量化标准进行了归类，均分为5个等级[23]，Ⅰ、Ⅱ、Ⅲ、Ⅳ和Ⅴ级分别表示围岩处于稳定、基本稳定、局部稳定、不稳定和极不稳定5个状态，最后确定出的珠江三角洲水资源配置工程B4标段围岩稳定性预测指标体系见表2。

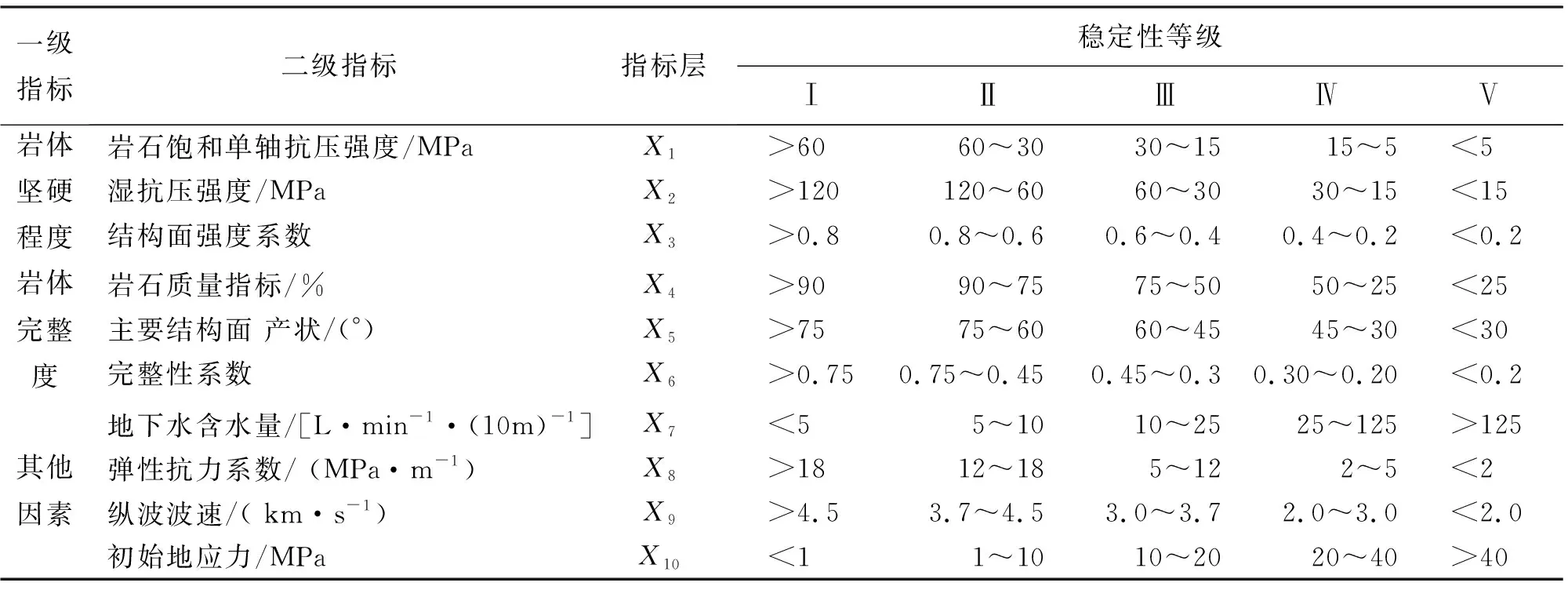
表2 珠江三角洲水资源配置工程B4标段围岩稳定性预测指标体系

3.2 数据收集与处理

按照主要结构形式和地质岩性的分布选取9个典型隧洞断面进行计算分析，根据《工程测量标准》(GB 50026—2020)、《工程岩体分级标准》(GB/T 50218—2014)的指标量化细则、实地测量、实验数据等资料，收集处理得到的围岩信息如表3所示。

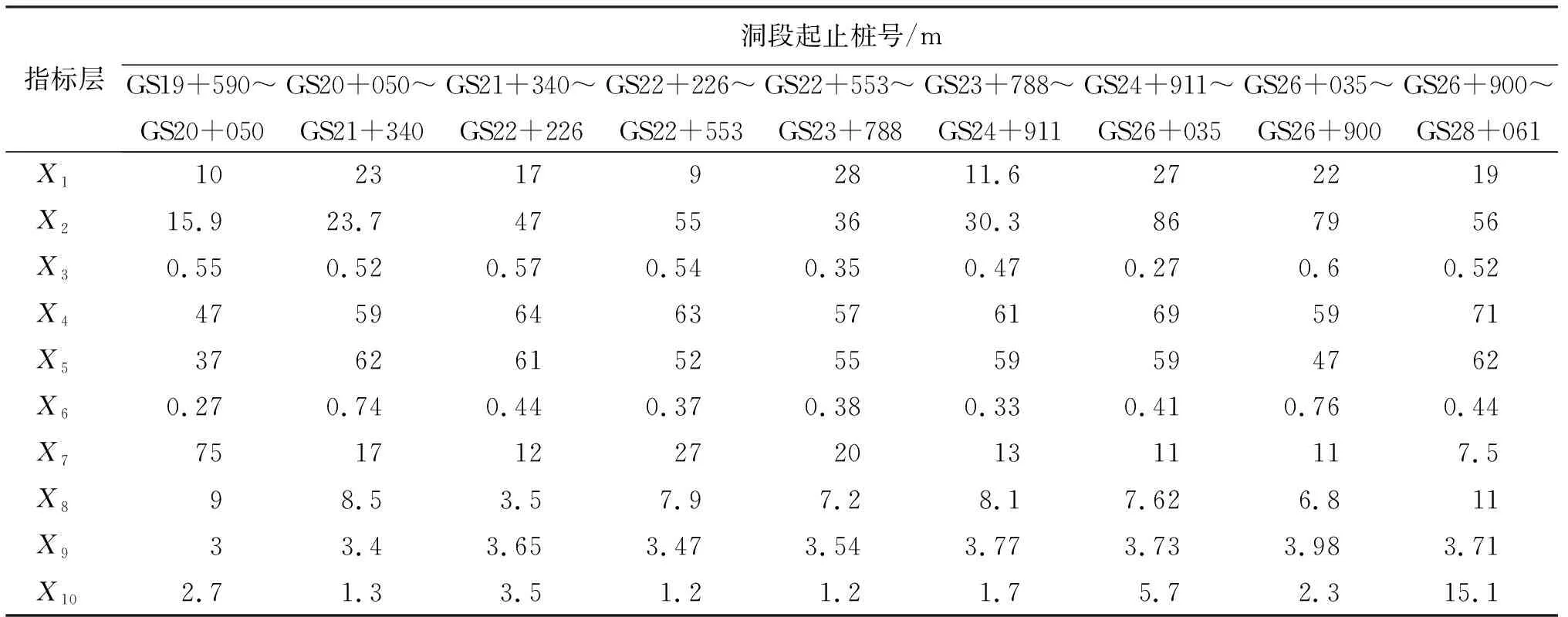
表3 珠江三角洲水资源配置工程B4标段各洞段围岩信息表

3.3 构建改进G1-RS-UMT预测模型

3.3.1 组合赋权

(1) G1法计算主观权重W1。根据表2珠江三角洲水资源配置工程B4标段围岩稳定性预测指标体系，向多位专家进行咨询，回收问卷并分析计算。W1=(0.0182∶0.0130∶0.1503∶0.2886∶0.1252∶0.2405∶0.0489∶0.0783∶0.0218∶0.0349)

(2) 改进RS法计算主观权重W2。由2.1.2节计算得W2=(0.1399∶0.1049∶0.1405∶0.0340∶0.0340∶0.0690∶0.1049∶0.1305∶0.0992∶0.1431)

(3) 运用博弈论计算组合权重W*。组合权重W*计算结果如表4所示。

表4 组合权重计算结果表

3.3.2 改进G1-RS-UMT预测模型

Step 1单指标未确知测度的计算。根据每个指标的未确知测度函数和表2，构造测度函数如图1所示，用以求得单指标未确知测度。以第一个洞段GS19+590～GS20+050为例，得到其单指标未确知测度矩阵μ1 jt。

Step 2多指标综合测度评价矩阵的计算。由公式(15)计算得到9个隧洞断面的多指标未确知测度向量, 以洞段GS19+590～GS20+050为例, 其他洞段同理可得，由于篇幅原因没有罗列，μ1t=(0.0396,0.0699,0.3460,0.5052,0.0393)。

Step 3置信度识别准则。本案例水工隧洞围岩稳定性的预测等级空间A={A1,A2,A3,A4,A5}满足At>At+1(t=1,2,3,4)，置信度λ=0.5。对于第1个洞段GS19+590～GS20+050有tc=min{0.0396+0.0699+0.3460+0.5052=0.9607>0.5} =4，故判定该段围岩稳定性预测等级为Ⅳ级。同理可以得到其他洞段的等级结果，珠江三角洲水资源配置工程B4标段水工隧洞围岩稳定性预测等级见表5。

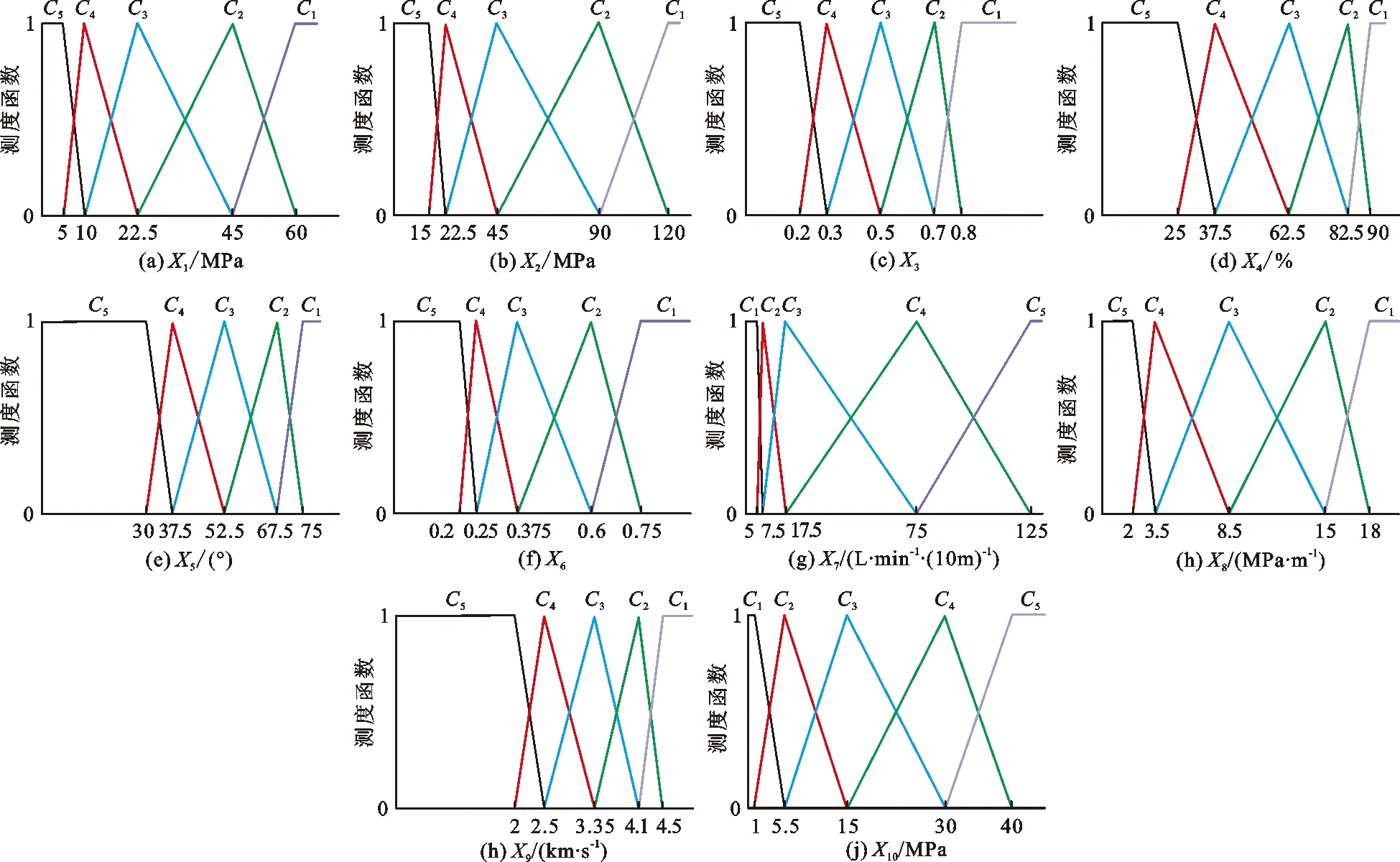
图1 各指标测度函数

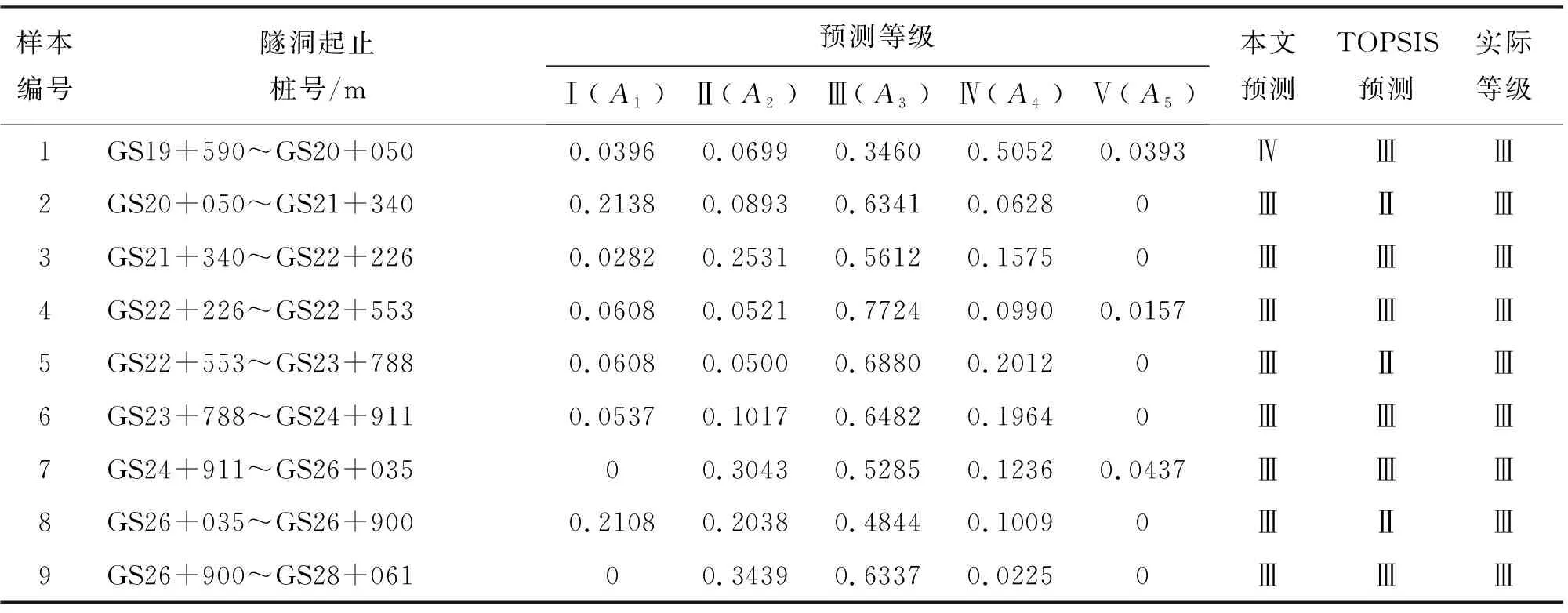
表5 珠江三角洲水资源配置工程B4标段水工隧洞围岩稳定性预测等级

3.4 结果分析

(1)通过计算结果可知该单线输水隧洞除里程范围为GS19+590～GS20+050段围岩等级为Ⅳ级，里程范围为GS20+050～GS21+340 、GS21 + 340～GS22+226、GS22+226～GS22+553、GS22 + 553～GS23+788、GS23+788～GS24+911、GS24+ 911～GS26+035、GS26+035～GS26+900、GS26 + 900～GS28+061段围岩等级皆为Ⅲ级。与地质资料中的实际等级相比，除GS19+590～GS20+050段以外其他各段围岩预测等级均相同。

(2)由图2和表5分析可得，改进G1-RS-UMT模型相比于TOPSIS(technique for order preference by similarity to an ideal solution)模型，围岩稳定性等级预测结果与实际等级相符合程度从66.67%提高到88.89%。改进G1-RS-UMT模型为围岩稳定性等级预测提供了一种新方法，可应用于珠江三角洲水资源配置工程的输水隧洞围岩稳定性等级预测问题中。

(3)基于改进G1-RS-UMT模型的预测结果，给出水工隧洞施工及支护方案设计的建议，其中Ⅲ级围岩采用全断面开挖法，炮孔周边间距不大于50 cm，开挖进尺应不大于3 m，洞室开挖过程中支护措施如下：①初次支护采用C15喷射混凝土，厚10 cm；②Φ22注浆锚杆，间距为2.0 m × 2.0 m；Φ8.0钢筋网，间距为15 cm×15 cm；③二次支护采用C25钢筋混凝土，厚度为20 cm。Ⅳ级围岩采用全断面开挖法，炮孔周边间距不大于40 cm,开挖进尺应不大于2 m，洞室开挖过程中支护措施如下：①初次支护采用C15喷射混凝土，厚15 cm；②Φ22注浆锚杆，间距为2.0 m×2.0 m，顶部180°范围内梅花型布置；局部采用20a型钢格栅拱架；③二次支护采用C25钢筋混凝土，厚度为35 cm。

4 结 论

(1)影响水工隧洞围岩稳定性的因素错综复杂，在既有研究和规范的基础上，构建了包含10个代表性指标的珠江三角洲水资源配置工程的水工隧洞围岩稳定性预测指标体系。

(2)由于该工程的水工隧洞围岩稳定性预测属于典型的有序分割类问题，且各评价指标信息具有模糊性和不确定性，因此在围岩稳定性等级预测模型中引入UMT，并提出了改进G1-RS-UMT模型。本模型相比于TOPSIS模型其准确度更高，预测结果与实测等级结果相符合程度由66.67%提高到88.89%，验证了该模型预测结果的可靠性。

(3)随着智能设备的普及化，可以将改进G1-RS-UMT模型设计成手机APP的形式，实现在勘察设计和施工阶段的水工隧洞围岩稳定性预测和分析，以便快速做出施工及支护方案的改进。