金属铑的反演势构建和应用
2021-02-13任县利周建仁王塞北陈静洪毕亚男
任县利,陈 松,周建仁,谢 明,王塞北,陈静洪,毕亚男
(昆明贵金属研究所 稀贵金属综合利用新技术国家重点实验室,昆明 650106)
原子间相互作用势是凝聚态物质在原子尺度上进行计算模拟的基础,特别是使用分子动力学等方法对物质的结构和性质进行模拟研究时。获得精确的原子间势函数一直是模拟计算的重点和前提,并直接决定了模拟结果的准确性和有效性。陈氏晶格反演势理论,作为一种对势理论,已经被广泛的应用于各种材料的研究中,包括金属间化合物,金属陶瓷,离子晶体,半导体和金属氢化物[1-5]等材料领域。陈氏晶格理论以数论中的莫比乌斯理论为基础,可以获得中心原子与任意近邻下的原子之间的相互作用,从而得到精确的原子间相互作用势,反演过程以数论为基础,不含经验成分,得到的结果是准确有效的。而传统的多体势模型如EAM 势(嵌入原子势),势函数中包含的参数往往通过拟合实验数据获得,含有较大经验性,并且在不同条件下,参数的值不同。同时,对于不同种材料,对应有不同的势函数形式。所以多体势模型往往普适性不强[6-8]。
本文以贵金属铑为研究对象,基于第一性原理和陈氏晶格反演理论,构建铑的精确反演对势。并利用对势的计算结果计算铑的声子谱以验证其有效性和可靠性。计算铑的线膨胀系数等物理量,为铑的研究尤其是在工程应用上的研究提供参考。
1 计算过程
1.1 反演势的构建
基于莫比乌斯理论,陈氏晶格反演方法[9]将得到的晶格内聚能反演,从而得到原子间的对势,可以总结为以下两个函数之间的转换。如果:
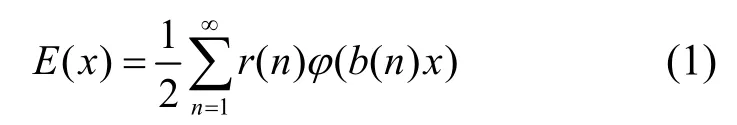
其中E(x)为原子内聚能,x为最近邻距离,r(n)为第n近邻原子的配位数,b(n)为第n近邻原子的相对距离,那么:
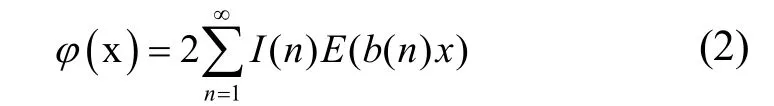
函数(2)中的I(n)为反演系数,可以通过式(3)计算:

集合{b(m)}满足乘法半群,并且通过计算机编程使得b(1),b(2)…b(n)按从小到大排序,并且b(1)=1。b-1[b(m)/b(n)]是一种数学运算,表示当b(m)/b(n)的值属于集合{b(m)}并等于b(k)时,那么该运算得到的值即为k。计算使用 Material Studio 软件中的CASTEP 模块,采用基于局域密度近似(LDA)的赝势,计算了fcc(面心立方)金属铑在不同原子距离下的孤立原子基态能。计算过程中布里渊区k空间网格划分为16*16*16,截断能设置为340 eV,迭代过程收敛精度选择1*10-5eV。计算选取的价电子为4d85s1,计算过程不考虑自旋极化[10-12]。孤立原子基态能计算结果如图1 所示。采用式(4)函数:
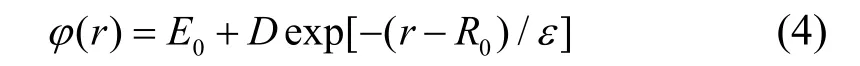
对图1 所示曲线进行拟合,其中E0表示孤立原子的基态能且有E0Rh= −601.483 eV。

图1 铑的孤立原子基态能曲线Fig.1 The isolated atomic ground state energy curve of Rh
在相同的参数设置条件下,在铑的fcc 晶格原胞中计算原子距离从0.2~0.7 nm,步长为0.01~0.05 nm 共计40 个格点的内聚能。并减去基态能的值即得到晶格内聚能曲线。如图2 所示。根据以上计算结果用自编程序计算得到原子距离从0.2~1.2 nm,步长为0.02 nm 的晶格反演势曲线,如图3 所示。

图2 铑的晶格内聚能曲线Fig.2 The lattice cohesive energy curve of Rh

图3 铑的晶格反演势曲线Fig.3 The lattice inversion potential curve of Rh
1.2 反演势曲线的拟合
精确的拟合函数,尤其是全局性符合程度高的函数,是下一步精确计算的基础。采用Origin 软件对图3 所示曲线进行拟合,拟合质量通过软件给出的相关系数进行评估。相关系数的值在0~1 之间,值越接近于1,表明拟合的效果越好。本文分别采用Rose 函数,Morse 函数及本文提出的新型的双指数型函数对反演势曲线进行拟合,并对拟合结果进行对比和分析。
1.2.1 Rose 函数和Morse 函数的拟合
Rose 函数常被用来做对势函数的拟合[13],其函数形式如下:

其中D、R0和α为拟合得到的参数,φ(r)表示对势势能,r为最近邻原子距离。拟合得到的相关系数值为0.99781,可见拟合质量符合要求。
Morse 函数已被广泛运用于fcc 金属的对势函数的拟合中,其函数形式如式(6)。
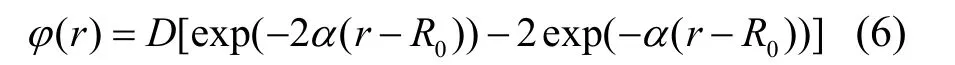
拟合得到的参数值如表1 所列,表1 中同时将计算得到的数据与Flahive 等[14]计算的数据对比。
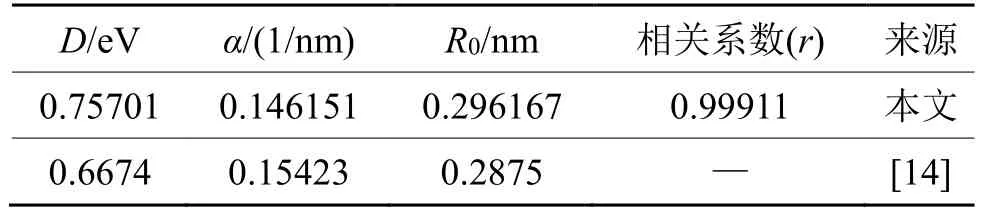
表1 利用Morse 函数拟合得到的铑参数对比Tab.1 Fitting parameters in Morse potential function of Rh
对比发现:R0和α的值相对差别较小,而D的值相差较大。这主要是两者选择的计算温度不同,本文计算选取0 K 为基准态;而文献[14]的数据计算基准态为气态,并且文献[14]中R0由平衡态最近邻原子距离决定,α与势函数的二阶求导有关,尽管随着温度的变化,原子间距离会以平衡态最近邻距离为中心做热振动,导致晶格常数发生改变,但根本上平衡态最近邻原子距离始终保持不变,所以当拟合选取的温度不同时,这两个参数的值差别较小。而D值与势函数对应的最低势能有关,由势函数选取的基准态决定,并且气态条件下,基准态能量要小于0 K 时孤立原子的基态能,所以导致了D值有0.0896 eV 的偏差,且文献[14]对应的值较小。所以本研究得到的势函数是准确有效的。
1.2.2 双指数型势函数的拟合
为了进一步提高函数拟合精度,本文提出了包含有5 个参数的双指数型势函数,其形式如下:

拟合得到的相关系数为1,表明拟合精度高,得到的参数如表2 所列。

表2 利用双指数型函数拟合得到铑的参数Tab.2 Fitting parameters in double exponential potential function of rhodium
为了对比和分析3 种函数拟合对势曲线的效果,将其拟合结果进行放大观察和分析。如图4 所示。结果表明,Rose 函数和Morse 函数虽然在对势函数曲线的长程段和短程段拟合效果较好,但是在曲线的拐点附近与曲线的一致性符合较差。所以两个函数的全局性精度相对不高。而本文提出的双指数型势函数,在拟合的全局上表现非常优异,且相关系数为1,表明拟合精度很高,为下一步的精确计算,提供有力的基础。
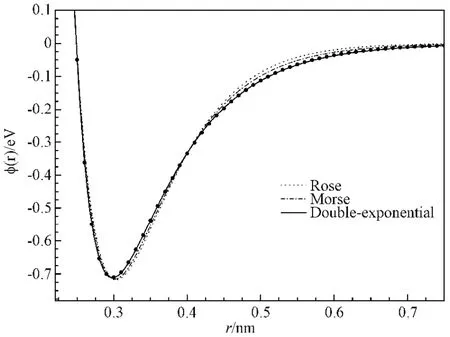
图4 三种势函数拟合结果的比较Fig.4 The comparison of the fitting results of these three potential functions
2 应用和分析
2.1 铑的声子谱的计算
为了验证对势函数的有效性,通过Material Studio 软件中的GULP 模块分别采用反演对势方法和EAM 势中的Sutton-Chen 多体势方法以及通过软件中的CASTEP 模块(采用有限位移法)计算了铑的声子谱,如图5 所示。
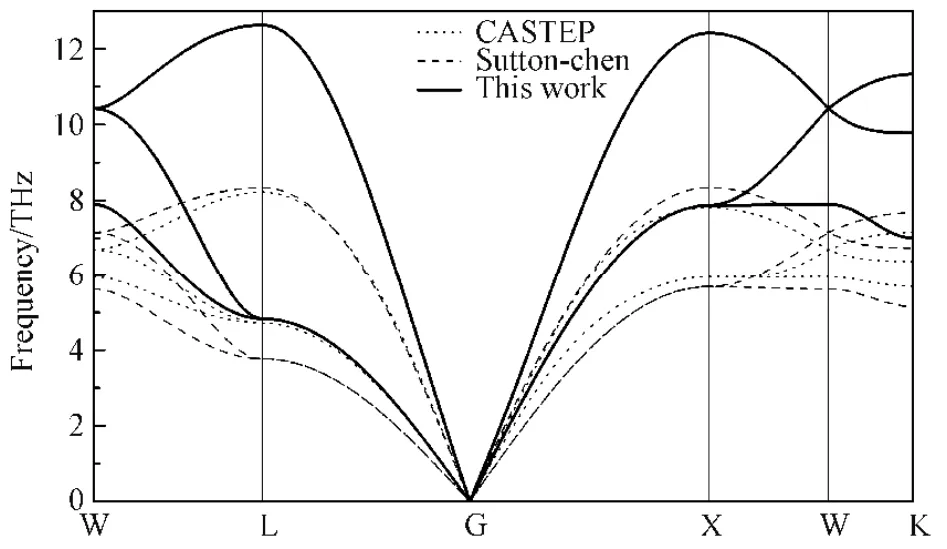
图5 铑的声子谱Fig.5 The phonon spectra of Rh
布里渊区对称点坐标为G(0, 0, 0)、X(0.5, 0, 0.5)、W(0.5, 0.25, 0.75)、K(0.75, 0.375, 0.375)、L(0.5, 0.5, 0.5)。结果表明,三种方法对应的声子谱曲线的变化趋势是相似的,表明反演对势可以有效的反应原子间的相互作用。同时,采用Sutton-Chen 方法计算声子谱时所需的时间比对势方法所需的时间要多40倍,说明对势函数在计算量上有明显的优势。
对于不同的材料体系,EAM 势的函数模型不同且均包含有经验成分[15]。并且其函数推导过程往往以Rose 函数为基础,导致在后续的计算精度不够。而反演对势函数基于数学理论,通过严格的数学证明,不含有任何经验成分,是一种全局精确的势函数。对于声子谱的计算结果也是有效和可靠的。
2.2 势函数的应用和计算
采用式(8)双指数型函数对图2 所示的铑的晶格内聚能曲线进行拟合,拟合得到的参数如表3,拟合相关系数为0.99996。


表3 利用双指数型函数拟合内聚能曲线得到的铑参数 Tab.3 Fitting parameters of cohesive curve using double exponential potential function for rhodium
对该函数求一阶导数,并令其值为0,得到0 K下,平衡态原子最近邻距离r0Rh= 0.2686139 nm。在此基础上,分别计算了铑的线膨胀系数,体弹性模量以及格林乃森常数等物理量,并与实验数据进行对比和分析。
2.2.1 线膨胀系数的计算
本方法基于计算得到的势函数的解析式以及玻尔兹曼分布函数[16],计算在不同温度下,铑的热振动平均位移。

其中δ=r−r0,r0为0 K 下平衡态原子最近邻距离。考虑到原子距离不可能为负值,且从a到∞变化,其中a为铑的离子半径。

由于线膨胀系数是一维物理量,V(r)应为一维原子链上的势能,而公式(8)中的u(r)为原子间总能,是三维的量。所以V(r)与u(r)之间的关系应为

将式(8)及表3 中的数据代入到式(10)中,用自编程序计算得到273~373 K 范围内不同温度下的原子平均热振动位移的数值解。结果如图6 所示。
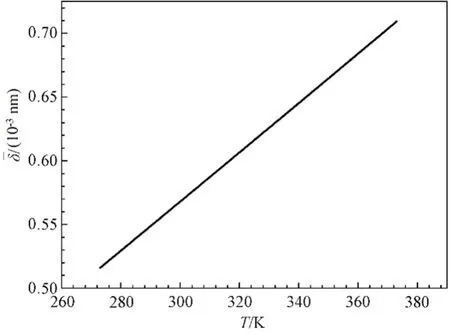
图6 铑的原子热振动位移-温度曲线Fig.6 Relationship between average atomic thermal vibration displacement and temperature curve of Rh
由式(12):

计算得到273~373 K 温度段的铑的线膨胀系数的平均值为αLRh=0.71978×10-5K-1。与文献[17]实验数据对比αLRh=0.85×10-5K-1,计算结果的相对误差为15.3%,说明计算数据与实验数据相比基本符合,但值较小。这主要是因为忽略了金属自由电子气的影响。根据格林乃森方程:

其中κ为体弹性模量,αV为体膨胀系数且与线膨胀系数之间的关系为αV=3αL,γ为格林乃森常数,CV为定容比热容。金属的比热容包括晶格比热容和电子比热容两部分[16],其表达式如下:

当温度高于德拜温度时,晶格比热容起主导作用,但是当温度较低时,电子对金属的比热容会有显著贡献,所以在273~373K 范围内,金属自由电子对比热容的影响不能忽略。所以导致计算结果值偏小。
但该计算方法是有效且十分有意义的,传统的计算线膨胀系数的理论方法,主要依靠近似原子间作用势和分子动力学方法等,每种方法都有自己的假设,许多假设只有在有限的温度范围内才有效[18],且计算量大,流程复杂。本方法结合原子间相互作用势和玻尔兹曼分布函数,计算量小,步骤简单,具有一定精度,适合实际使用。
2.2.2 体弹性模量的计算
体弹性模量和原子间相互作用势的关系[19]可以用下式表示:

其中U为原子内聚能,V为单个原子在fcc 晶格结构中所占的体积,所以有:

将公式(8)带入到上式得:
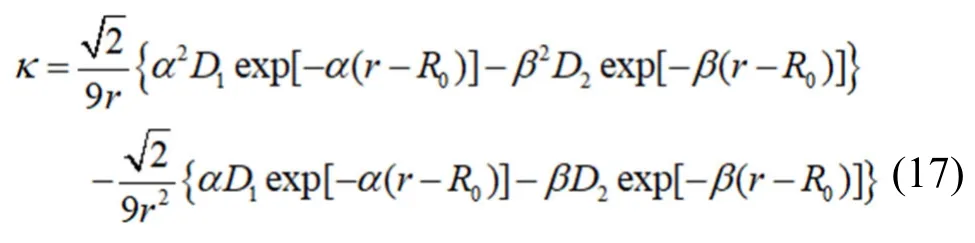
由公式(10)计算得到在室温293 K 下原子的平均热振动位移为δ-Rh=5.51×10-4nm,所以室温下原子平衡态最近邻原子距离为r0'=0.2719819 nm,r0'由公式r0'=r0+δ-计算得到。带入到公式(16)中,得室温(293K)下铑的体弹性模量为κRh=3.132099×1011N·m-2,与实验数据[17]κRh=2.76×1011N·m-2对比,误差为13.5%,说明计算结果是准确有效的。
2.2.3 格林乃森常数的计算
基于公式(13)及铑的线膨胀系数和体弹性模量的计算值,其中体积V 通过下式计算:

NA为阿伏伽德罗常数,r0为平衡态最近邻原子距离。且CVRh=24.98 J/mol·K,计算得到293 K 下,铑的格林乃森常数为γRh=2.25,与实验数据[17]对比γRh=2.26,相对误差为0.8%,说明得到的势函数势准确有效[20-23]。
3 结论
1) 以第一性原理计算为基础,通过陈氏晶格反演方法,得到了fcc 金属铑的精确的晶格反演对势曲线,并采用本研究提出的双指数型势函数对曲线进行拟合,得到对势函数的精确解析式。
2) 分别采用反演对势函数,Sutton-Chen 函数及有限位移法计算了铑的声子谱,对比发现本文得到的势函数是有效的。
3) 提出了基于反演势和玻尔兹曼分布函数计算线膨胀系数的方法,计算了铑的线膨胀系数、体弹性模量和格林乃森常数,与实验数据的对比相对误差分别为15.3%、13.5%和0.8%。表明本研究提出的计算方法是准确且有效的。
