分布式电驱动汽车复合制动控制策略

刘 畅，杨涛涛，王式民

（枣庄科技职业学院，山东枣庄 277599）

0 引言

以电能为主要能源的新型能源汽车已成为最新的研究方向，具有独立可控的电动轮转矩、系统响应快、控制精准且容易是分布式电动汽车的特有优点，已经得到业内人士的高度重视，且成为重点研究方向。需注意的是，新能源电动汽车存在续航里程短、充电慢、能量利用率不高等问题，而这些问题是目前最需要克服和突破的关键点。复合制动系统能有效回收制动能量，促使动能转化为电能，在解决能量利用率低的同时，增加了续航里程。

1 下层控制器设计

粒子群优化算法自1995 年被提出以来，得到社会各界的高度关注，该阶段主要应用于鸟类觅食行为的研究中，后续逐步发展，理念及方法得以持续更新。在粒子算法的理念中，将优化问题的潜在解均视为多维空间中的某个点，将其称之为“粒子”，并且通过目标函数的应用，任何粒子都有其适应值，同时也存在特定的飞翔方向与距离的速度，此条件下，粒子将朝着最优粒子在解空间内进行搜索。在该类算法的视域下，衍生出下层控制器，其设计要在满足上层控制器要求的同时，缩减车辆能耗。在车辆制动的过程中，动能原本转变为热能，而依托于电机的再生制动，可以实现部分动能向电能的转换。因此，制动时要优先使用电机再生制动。

2 上层控制器设计

2.1 基于变论域模糊比例积分的上层控制器设计

在该控制器中，输入指的是横摆角速度的期望值与实际值的差值，输出指的是附加横摆力矩，运行流程如图1 所示。

图1 变论域模糊比例积分控制器结构

2.2 变论域模糊控制器

相比而言，车辆稳定性控制比较复杂，在分析时从组织概念着手，引出模糊控制器，通过对控制器性能的全面检测，促进模糊论域范围自动调整目标的最终实现。模糊控制机制下，若系统从非理想状态转变为理想状态，此时偏差的实际值将有明显减小的特点，同时分布区的跨度也减小，集中在初始论域的某个特定的小区间内。若偏差值仅存在微小的变化，此条件下控制量也偏小，很大程度上也会固定在一个值长久不变。理想状态应该是系统逐渐变得稳定，其整个偏差的实际值只会越来越小，而此时的论域也会不断压缩；反之，随着偏差实际值的扩大，论域也会不断扩大（图2）。

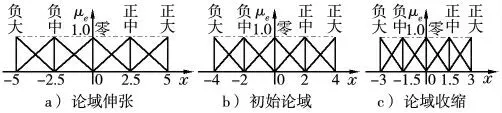
图2 论域伸缩过程

3 建立复合制动控制模型

在分层分配中，上层控制器的核心作用在于有效维持制动的可靠性，以实际条件为立足点，因地制宜地为各车轮分配相适配的制动力；下层控制器的关键功能在于尽可能实现能量回收最大化的目标，其又可细分为两个层面，即液压制动力与电机制动力，使其可以满足各车轮的要求，也能够立足于实际条件针对两类制动力做出调整，优化其在车轮上的比重关系和动力在每个车轮上的占比。首先要保证前后轴制动力的分配精确，为确保制动效果和质量均处于最优状态，分配前后轴的制动力要按照I 曲线进行。同时，考虑到车辆方向的稳定性要求，如不出现跑偏和位移等，需要以合理的方式向各轴的左右车轮分配制动力，必须确保制动力的分配具有均匀性，否则易出现横摆力矩或是其他异常状况。

在制动期间相较于最佳滑移率而言，若车轮产生的实际滑移率未大于该值，ABS 系统就不会被触发且保持运作；相反，若车轮的具体滑移率超过最初的最佳滑移率，ABS 系统就会被触发且保持持续的运作，实现对车轮制动力矩的动态化调节，使滑移率可维持相对合理的区间内。制动力矩分配模型能够确定电机所需的最大制动力，考虑到制动能量回收的效率要求，应当注重对制动力使用顺序的控制，即首先宜使用电机制动力，若该部分制动力难以完全满足要求，则借助液压制动力对空缺部分进行补充。

4 建立复合制动系统模型

在复合制动模型的组成中，以制动轮缸尤为关键，需要在AMESim 中建模。结合制动缸的工作原理和内部结构构建模型，如图3 所示。

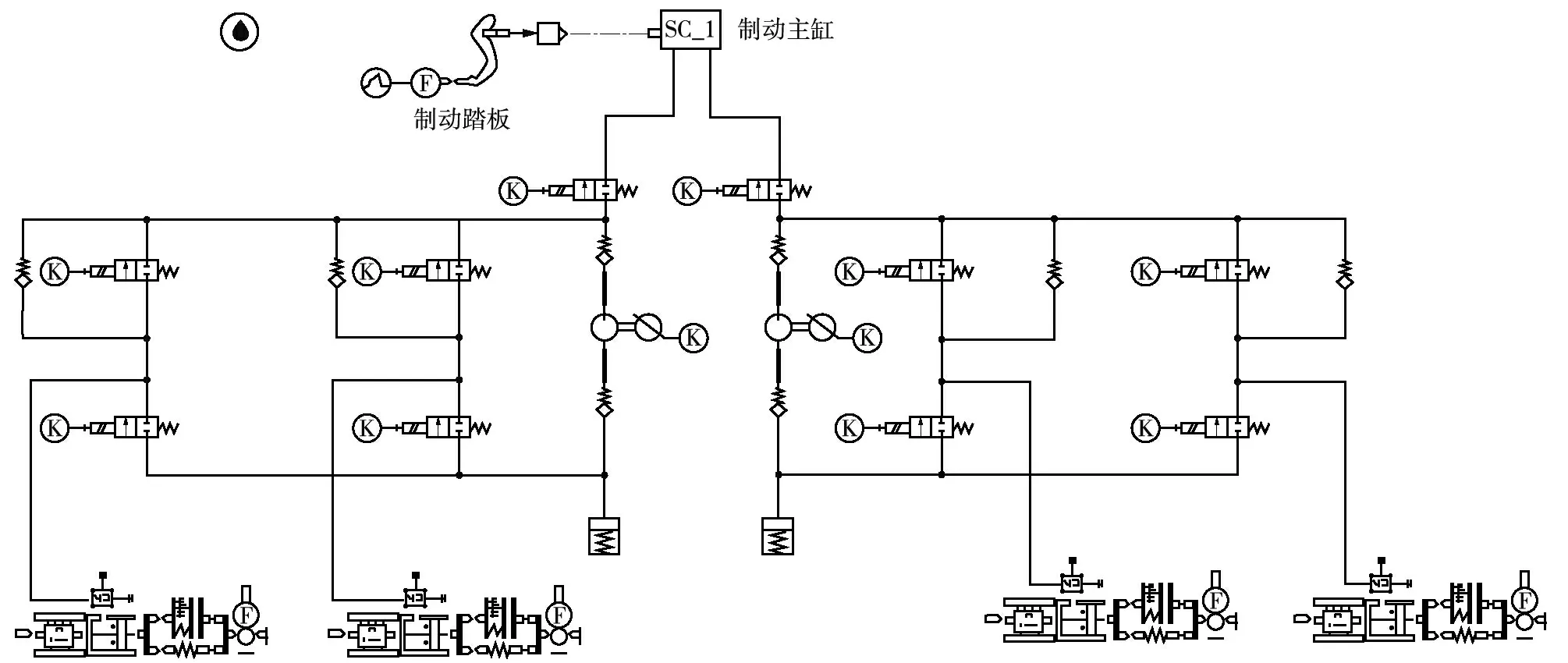
图3 ABS 模型

活塞的动力学方程为：

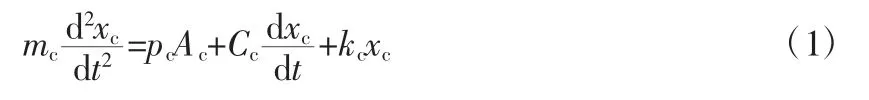
式中 mc——制动钳的质量，kg

xc——制动钳与制动盘间的测量距离，m

pc——轮缸压强，Pa

Ac——轮缸活塞横截面积，m2

Cc——等效阻尼

kc——等效刚度，N/m

现阶段的汽车行车制动系统的配套中，应用较为广泛的当属双回路制动系统，而该系统的功能得以正常实现的前提在于可靠的串列双腔制动系统。

制动主缸推杆推力与主缸内油液压力两项参数间存在密切的关联，具体如下：

式中 Fm——推杆推力，N

Pm——制动主缸压强，MPa

Am——与主缸等效的横截面积，m2

Fms——回位弹簧力，N

Fmf——缸壁摩擦阻力，N

制动主缸、制动踏板、控制器、回油泵、蓄能器、单向阀、开关阀、制动轮缸是构成液压系统的主要部件。

5 仿真结果

仿真工况中，绝大部分情况下将路面的附着系数取为0.7，同时初速度为72 km/h，但就实际试验环境来看，其经常会使用0.8 的制动强度来进行制动。如图4 所示，车速从72 km/h 降至0 所耗费的时间约为3.3 s，由此推断制动时间为3.3 s。在整个制动过程中，0.4 s 为明显的分界点，前后具有阶段性变化的特征。前0.4 s 的制动强度相对较小，此时只需要较小的制动力矩，因此前0.4 s 只依靠电机进行制动，整个液压制动系统并不参与车辆的制动工作，这可解释前0.4 s 内电机制动力矩直线增加而后轴液压制动力矩是0 的问题。一旦超过0.4 s，制动强度会快速增加，此时仅依靠电机产生的制动力矩根本满足不了制动的需求，液压系统会自动开启，自动补全制动力矩空余的部分，这时车辆的制动便属于电液复合制动模式。当整个制动作业推进到1.3 s 之后，电液复合制动的性能已经达到极限，但仍难以满足强度要求，在此运行环境中，电机不再保持制动状态。随着ABS 系统的介入，可以发挥出强有力的控制作用，有效控制前后轴车轮的滑移率，即稳定在最佳滑移率附近，并未出现过分的偏差。这也从侧面证明在复合制动系统的模型中，ABS 系统能产生较好的工作效果和质量。在最初的1.3 s 内，系统内部的工作机制具有协同性，即纯电机制动和电液复合制动两者协同。由于电机的参与，制动能量的回收率较高，促使电池的SOC荷电状态值发生变化，即从50%增至50.4%；而在该时间之后（1.3 s 后），电机不再继续参与到制动工作中，能量回收进程结束，此时可以发现电池的SOC 值维持在恒定状态。

图4 车速变化曲线

6 结果分析

以AMESim 和MATLAB 为主要分析平台，建立复合制动系统模型和制动控制模型，经仿真操作后，得到在特定工况下的具体图形结果，即制动距离曲线、制动力分配曲线、滑移率曲线及电池SOC 值变化曲线。本文搭建起来的复合制动系统和制动控制系统，能结合制动的实际工况合理分配制动力矩。同时由于ABS 的介入，可以较为可靠地控制滑移率，避免出现大幅度波动的情况，实际值可控性好，稳定在最佳滑移率附近，并在最大程度上实现制动能量的回收。