二维变量约束条件下的多属性群决策方法及应用

朱国成，赵瑞华

（1. 广东创新科技职业学院 通识教育学院， 广东 东莞 523960； 2. 云安中学 生物组， 广东 云浮 527500）

0 引 言

针对属性权重与属性值皆为实数的多属性群决策问题，国内外学者均通过定义集结算子实现信息融合：为了将众多属性信息融合，文献[1]建立了有序加权平均算子（OWA）模型，该模型的显著特征是第i 大变量赋予第i 个属性的权重，该算子取值在“求极大”和“求极小”之间；在OWA算子基础上，文献[2]证明了一般情况下所有OWA算子与Chquet 积分都可相互转换，具有普通等价关系；文献[3]建立了WOWA 算子模型；文献[4]定义了OWG 算子并在多属性群决策问题中验证其有效性；文献[5]根据OWA 算子的主要性质特点，拓展其应用范围，建立了IOWA 算子模型；陈华友等[6]在HOWA 算子基础上，进一步建立了有序加权调和平均算子模型；在OWA 算子基础上延伸出的新算子，还有GOWA[7]算子与IOWGA[8]算子等。

目前，有关实数信息集成手段研究较为成熟，应用也很全面。不同于传统多属性群决策方法，文献[9-10]将实数构成的属性值转化为区间直觉模糊数，利用新定义的集结算子进行融合；文献[11]将属性的具体实数值转化为区间数，再利用区间数排序准则，对各方案的属性进行比对，由此对各方案决策。

有别于前人研究，针对属性值为精确数的多属性群决策问题，本文未采用集结算子对属性信息进行融合，而是构建属性取值区间和权重取值区间，利用平均权重对属性权重区间加以整合，同时利用加权的专家组评分构成属性值取值区间，对于不同的方案，属性权重与属性值的取值是动态的。在此基础上，通过建立二维变量下的线性规划模型对各方案求解极大值，以此作为综合属性值进行比对决策。

1 多属性群决策方法构建

需要指出的是，上述排序方法没有在统一属性权重与属性值下得出各方案的综合属性值，从表面看有违决策公平，但属性权重及属性值在统一区间内动态取值，根据方案自身特征得出最优化结果，实际又是公平的。

2 案例分析

以教师课堂教学质量评价为例，说明上述方法的实际应用。设在教学评价中有4 位督导专家Ak（k = 1，2，3，4）构成评价专家组，对6 位教师Fj（j=1，2，…，6）进行评教，督导专家评分权重为（λ1，λ2，λ3，λ4）=（0.32，0.26，0.22，0.20）。有 m=14项评教因素，具体含义如下。

G1：精神饱满，仪态大方，仪表端庄，按时上下课；

G2：教学文件齐全，课件制作精美；

G3：提前到课室做好上课准备；

G4：教学目标明确（含知识目标、能力目标）；

G5：教学内容符合课标要求；

G6：执行教学计划，进度适中；

G7：观点正确，概念清楚，例证恰当，信息量适中；

G8：重点突出，难点讲解清楚；

G9：教学组织得法，教学形式合理，运用教学新技术、新载体，时间控制合理；

G10：表达清楚，讲解生动，语音、语速适中；

G11：严格课堂管理，做好学生考勤，及时纠正课堂上的不文明、不规范、不听课、不守纪现象；

G12：理论联系实际，深入浅出，注重运用创新教学方法，注重培养学生分析、解决问题的能力；

G13：课堂秩序良好，气氛活跃，教学互动效果好，学生学习积极性和主动性高；

G14：完成课堂教学任务，达到教学目的及要求。

各项评教因素Gi的评分范围事先给定为：i∈I′时[ai，bi]= [2，5]，i∈I″时[ai，bi]= [4，10]，其中I′={1，2，3，4，5，9，10，11}，I″={6，7，8，12，13，14}。专家组给各位教师的评分情况如表1 所示。

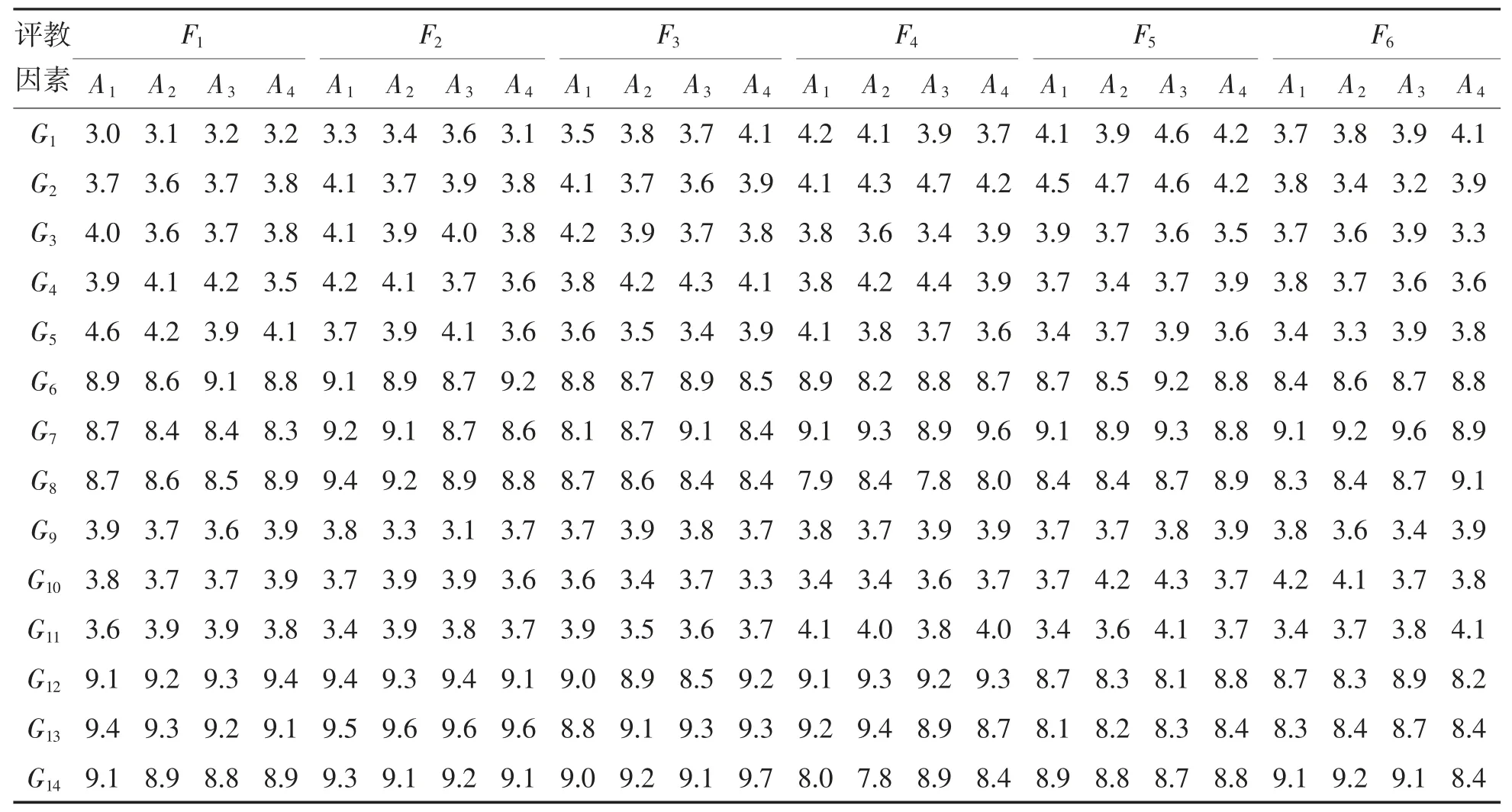
表1 专家评教评分表

运用上文所述方法，按步实施数据处理。

第一步：设立各评教因素Gi权重的取值区间。

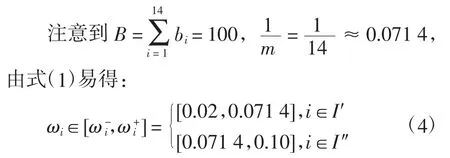
第二步：确定加权分pij的取值区间。

以教师F1为例，由已知的专家评分权重值（λ1，λ2，λ3，λ4）=（0.32，0.26，0.22，0.20），以及表1中对应F1的评分值qi1k，计算专家评分加权分λkqi1k（k=1，2，3，4），并按式（2）和（3）求出计算结果如表 2 所示。

类似地可以列出对其他教师F2—F6的专家评教加权分表。

第三步：对于每个方案，建立加权分的总量控制。

仍以教师F1为例，对表2 的最后一列求和，得到F1加权分的总量控制：

表2 专家评教加权分表

第四步：求解上文建立的线性规划max Z（Fj）=确定教师的综合属性值。

第五步：根据综合属性值的大小对方案进行排序。

比较第四步得到的max Z（Fj）（j=1，2，3，4，5，6）值，确定教师教学水平的优良排序为：

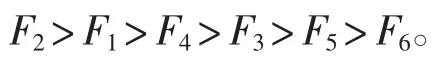
如果用传统的方法，将专家评价加权分直接相加获得综合评分值

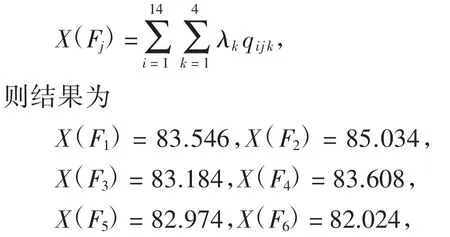
以此为依据得到各教师教学水平优良排序为：

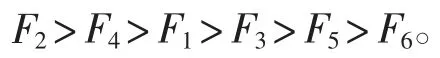
这与本文排序结果有出入，但最好与最差教师的位置未变。事实上，本文决策过程更注重教师的单个评教因素作用与专家认可程度，对教学水平处于中间位置的教师，其排序结果更富有弹性。

3 结 语

针对属性权重与属性值都为实数的多属性群决策问题，通过构造属性权重取值区间表达属性权重特征。为了更好地体现各属性的重要程度，利用平均权重对各属性权重进行适当整合，运用线性规划模型求解各方案的综合最优属性值。案例操作表明，该方法不仅可行，且提供了一种利用动态属性权重值进行群决策的思路，丰富了多属性群决策理论知识。