低段数学教学中“圈一圈”的价值分析与使用建议
2021-02-08费凤霞
费凤霞

【摘 要】低段数学教学中很多地方出现“圈一圈”。“圈一圈”可帮助学生获得直观的学习体验,促进学生内化概念,理解算理,掌握算法,有效构建笔算模型。在小学低段的学习中,教师通过“圈一圈”这一直观形式,引导学生从实物操作向數字运算过渡,在探索活动中促进学生对算理和算法的理解,发展了学生的思维。
【关键词】圈一圈;数感;算理;算法;模型
低段教学中很多地方都会出现“圈一圈”,圈一圈在教学中能起什么作用?对学生知识的学习和构建有何帮助?本文尝试解决这些问题。
一、寻理——“圈一圈”的价值
学者张天力说过:数学课程中的运算不再是单纯的技能训练,而是作为解决问题的组成部分,与问题情境相联系;不再按标准程序运算,而是寻求合理简洁的运算途径,倡导算法的多样化。
“圈一圈”介于操作和符号之间,是联通直观到抽象的桥梁,易操作。在教学中,“圈一圈”能有效帮助学生理解算理,掌握算法,建立算法之间、新旧知识之间的联系,形成直观操作、口算和笔算模型之间的纽带,为寻求简洁、合理的运算方法做铺垫,培养学生的运算能力。
二、探索——“圈一圈”的应用
笔者翻阅了北师大版的数学教材和课堂作业本,各册教材中都有与“圈一圈”有关的内容,主要体现在数的运算这一知识体系中(见下表)。
[册别 教学内容 圈一圈 一上 20以内数的认识
20以内数的进位加法 10个一圈
10根小棒一圈 一下 20以内的退位减法
100以内数的认识
100以内数的加减法(不进位,不退位)
100以内数的加减法(进位,退位) 借助小棒圈一圈 二上 乘法口诀
分一分与除法的认识
倍的认识
用乘法口诀求商 在点子图上圈
用小棒圈一圈
一份一圈
几个几个圈 二下 有余数的除法 平均分中的圈一圈 三上 一位数乘两位数
一位数除两位数 在点子图上圈一圈 三下 一位数除两位数
两位数乘两位数 借助点子图和小棒圈一圈 ]
这些内容的作用大致如下。
(一)圈一圈,内化概念
《义务教育数学课程标准(2011年版)》(以下简称《课程标准》)明确指出:“建立数感有助于学生理解现实生活中数的意义,理解或表述具体情境中的数量关系。”
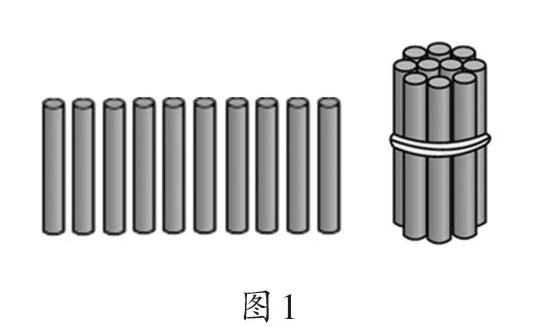
执教《20以内数的认识》时,为了让一年级学生理解“满十进一”的算理,教师将10根小棒捆成一捆(如图1),一根小棒、一捆小棒分别是1个一、1个十的实物直观形式。让学生“圈一圈”,既尊重了学生的认知起点,又促进了学生对十进制的直观理解。
习题中也多次出现圈一圈,10个一是十,那么10个一圈,一眼就能看出数量(如图2)。“圈一圈”属于实物操作,在“圈”的过程中学生的数感得到了培养。
“倍”的概念比较抽象,学生初学不易理解,需结合实物操作引入两个数量关系的比较,在头脑中形成两个数量之间倍数关系的直观表象。
在教学中,教师出示图3,让学生动手圈一圈,学生一眼看到图中有4只小猴、8只小鸭,教师引导学生用语言描述小鸭和小猴之间的关系,初步体会小鸭是小猴的 2 倍,以小猴为标准,小鸭有这样的2份,再放手让学生通过画一画、圈一圈等活动,发现小鸡是松鼠的 4倍(如图4)。
通过圈一圈,学生直观感受到比较两个数量关系,以其中的一个量为标准,另一个量有这样的几份,就是几倍,充分体会到了“倍”的内涵,在“圈”的过程中加深了对“倍”的理解。
(二)圈一圈,理解算理
《课程标准》指出:要想准确快速地进行运算,理解算理是基础。
“9加几”的进位加法是学生普遍反映的学习难点,也是学生加法学习中的第一个需跨越的障碍。进位不是经验思维而是抽象思维,为帮助学生清晰地理解算理,弄清为什么这样算,教师可让学生在事先准备好的学习单上圈一圈,学生主要有以下圈法(如图5、图6)。
两种不同的圈法,很好地呈现了学生的思维过程。圈法不一样,体现了学生不同的思考方法:一个是拆大数,一个是拆小数。教师让学生对比这两种不同的圈法,学生通过直观演示,很快能抽象出算理:不管哪一种方法,都是通过拆分来凑十,10个一圈。教师再让学生借助计算器拨一拨,其体现的算理实质都是满十进1。
授人以鱼不如授人以渔,学生初学进位加法时,“圈一圈”好比一座桥梁,让抽象的凑十法直观地呈现在学生眼前:10个一是十,满十进一。明白这一算理对掌握算法有促进作用,为后续理解两位数加一位数的算理提供了理论支持。
(三)圈一圈,掌握算法
《课程标准》明确指出:提倡算法的多样化,让学生经历“探究方法—明晰算理—掌握算法—总结算法”的过程是计算教学的主要特征。
教学“两位数乘一位数”这一内容,教师呈现了12×4的点子图,让学生圈一圈,算一算,并说说自己的思考过程——先算什么,再算什么,最后算什么,理解乘法竖式每一步的算法和算理。学生主要有以下几种算法:连乘、连加、拆成整十数和一位数(如图7)。
交流算法时,学生对每种圈法做出了合理的解释,进一步体会了算法多样化。在点子图上圈一圈,给学生提供了“素材”,帮助他们高效地达成“理解算理,掌握算法,能正确计算两位数乘一位数”的学习目标。学生明晰算法的来龙去脉,并且将此算法延伸到后续两位数乘两位数的学习中,真正做到了“知其然,更知其所以然”。
究竟哪种算法最简便呢?学生说法不一,为了让学生重点体会将12分成10和2这种核心算法的普适性,教师又出示23×7的点子图,让学生试着圈一圈并将计算步骤与点子图中圈的方法对应起来。学生在圈的过程中发现:23×7就无法用连乘的方法,用连加的方法计算起来也不是很方便,而将23拆分成20和3是最适用的方法。
