不同雷诺数条件下静止管道车环状缝隙流场数值模拟
2021-02-07贾晓萌孙西欢李永业
贾晓萌,孙西欢,李永业
(太原理工大学 水利科学与工程学院,太原 030024)
传统运输方式渐渐难以满足人们高速、便捷、绿色环保的发展理念,因此探寻高效、环保、节能的新型运输方式势在必行。基于此背景提出筒装料管道水力输送技术[1]。筒装料管道水力输送是以密闭容器为载体(一般为圆形料筒),以水为媒介,利用水压力将物体输送到目的地的一种新型运输方式[2]。当管道车在管道中处于静止状态时,水流流经管道车车体和支撑体属于类圆柱体绕流问题[3-7],而管道车车身壁面和管壁面形成的环状缝隙又属于环状缝隙流问题[8-9],由于黏性阻力的存在管道车车壁面处形成边界层,属于静边界层问题[10-12],当管道车在管道中运动时则又涉及到动边界和流固耦合等问题[13-20],同时筒装料管道输送技术还涉及自动化、交通运输等问题。因此,加强对筒装料管道水力输送技术的研究具有十分重要的意义。
目前,国内外学者已经对筒装料管道水力输送展开了研究。Mohamed等[21]分别运用代数模型、k~ω和k~ε模型对长直车体与管道形成的环状缝隙内的压力场进行了数值模拟,并通过物理试验进行验证,发现模拟结果同试验结果基本一致;Asim等[22]采用数值模拟的方法对水平方向和竖直方向运动的管道车所产生的压力场进行了计算,结果发现竖直运动的管道车环状缝隙内的压力梯度变化要大于水平运动;郑伟[23]通过模型试验对静止状态下不同导叶长度的管道车周身的环状缝环隙螺旋流进行研究,得出了管道车车身不同断面的压力变化和流速分布;吴剑等[24]对不同直径条件下的管道车车身环状缝隙流轴向速度进行了测量,发现随着车径的增加,环状缝隙流轴向速度增大且分布逐渐变得均匀;鲁一凡等[25]对不同缝隙宽度条件下的车后断面轴向流速进行了分析研究,发现随着环状缝隙宽度的增加,车后断面轴向流速变化幅度逐渐降低,且随着距离车后断面距离的增大,环状缝隙流轴向速度逐渐降低并趋于断面平均流速。
当管道车处于静止状态时,环状缝隙内的流速分布和压力分布会对管道车的启动状态产生影响,而雷诺数的大小又直接影响了环状缝隙内流速和压力的变化。因此,本文通过数值模拟、物理模型试验验证和理论分析相结合的方法对不同雷诺数条件下静止管道车环状缝隙流场进行研究,从而进一步丰富管道车环状缝隙流理论,为筒装料管道水力输送技术尽快实现工程应用提供一定的理论基础。
1 数值模拟设计
1.1 控制方程
数值模拟过程中假设流体为不可压缩黏性流体,则其连续方程(公式(1))和N-S方程(公式(2))如下:
(1)
(2)

由于管道内环状缝隙流为湍流,而对于充分发展的高雷诺数湍流,使用RNGk~ε湍流模型较为合适,其相关方程如下:
(3)
(4)
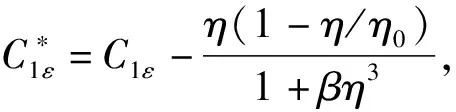
1.2 几何模型尺寸和相关边界条件
模型尺寸越接近于实际尺寸,数值模拟的准确度越高,同时为了减小运算量,在确保计算精确度的基础上,对模型进行适当的简化,通过Auto CAD软件进行模型构建,再将其导入ICEM中进行网格划分。试验模型主要包括管道车和圆形管路两部分(如图1所示)。管道车作为本次数值模拟的核心部件主要由圆柱形料筒和类圆柱形支撑体两部分构成,具体结构模型如图2所示。管道由内径为0.1 m、长度为2 m的有机玻璃管组成。管道车中心距离入口和出口的距离均为1 m(考虑到紊流的充分发展)。同时以水流流动方向为正方向,按照管道车与水流先后接触顺序将管道车车身等分为车前、车中、车后三个断面。

图1 几何模型

(a)管道车物理模型
根据公式v=Re·μ/ρd,分别求解不同雷诺数条件下的管道内水流平均流速,并将其作为速度入口的值代入计算模型。根据试验实测得到不同雷诺数条件下的管道出口处压力值,分别将其代入计算模型。
1.3 网格划分
本次试验采用1∶1等比例构建模型,由于管道车两端有支撑体存在,使得管道车整体结构相对复杂,为了提高试验计算精度,将整个系统划分为三个部分,即管道上游区域、管道车区域和管道下游区域,分别对这三部分进行网格划分。由于管道上游和下游区域内无管道车的存在,结构相对简单,在网格划分时所用尺寸相对较大,采用4 mm非结构化六面体网格进行划分,而管道车区域则采用1.5 mm的四面体非结构化网格进行划分。同时由于管道车自身结构会对环隙流场产生影响,为了计算的准确度,对管道车近壁面进行网格加密,壁面到第一层网格节点的距离为0.1 mm,共5层,层间递变梯度为1.2。
1.4 算法选择
由于SIMPLEC算法具有精度高、稳定性好、计算速度相对较快等优点,因此本次模拟的压力与速度耦合使用SIMPLEC算法。对流项采用二阶差分格式,动量方程、湍动能方程和湍流耗散率方程均采用二阶迎风格式。各项收敛精度设置为0.000 1。
2 物理试验设计
2.1 试验系统
为验证相关数值模拟结果的正确性,进行物理模型试验,试验系统如图3和图4所示。试验开始前先将试验水箱9注满水,并加入示踪粒子,之后将管道车固定于测试管段7,通过离心泵1将水箱中的水抽入管道当中,通过调节阀2和电磁流量计3调节试验所需流量,待管路内水流稳定之后,使用LDV激光流速仪进行测试,记录相应的试验结果。

1.离心泵; 2.调节阀; 3.电磁流量计; 4.管道车投放装置; 5.管道车制动装置; 6.电子计算机; 7.试验管段; 8.LDV激光流速仪; 9.试验水箱。

图4 试验管路和测试系统
2.2 测点布置
本次试验所用管道车尺寸为150 mm× 80 mm(长×直径),沿管道车车身方向每隔30 mm设置一个断面,共设置6个断面,在每个断面上分别布置测点。管道车与管壁之间形成同心环状缝隙,缝隙宽度L=10 mm,沿管径方向分别布置五个测环,如图5所示。沿直角坐标系顺时针方向每隔30°做管道半径(后称极半径)与测环相交,交点即为测点,共布置六十个测点。

图5 断面测点布置示意图
2.3 试验方案
本文研究不同雷诺数条件下管道车环状缝隙流流速分布状况,同时为便于物理模型试验进行验证,所选雷诺Re分别为:Re1=115 513、Re2=154 018、Re3=192 522,对应流量为30 m3/h、40 m3/h、50 m3/h,进行模型试验时可通过调节闸阀来改变流量大小,之后通过LDV激光流速仪对不同雷诺数下管道车环状缝隙流场进行测试。具体试验方案,见表1。
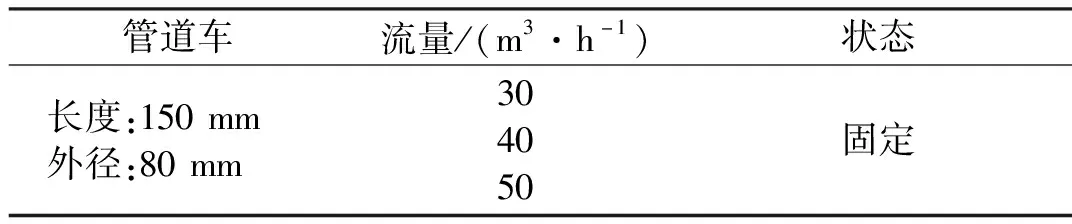
表1 试验方案
3 结果分析
3.1 环状缝隙流流速特性分析
本次试验对三种不同雷诺数下的管道车环状缝隙流场进行了数值模拟,管道内流速、环状缝隙流流速以及前后支撑体断面流速值如表2所示,同时选取雷诺数为Re2=154 018时的车前、车中和车后断面以及前后支撑体断面的三维速度分布云图(如图6所示)进行分析研究,其它雷诺数不做重复赘述。

表2 不同雷诺数下平均流速

(a)车前断面
从表2可以看出:当雷诺数一定时,环状缝隙内水流平均流速大于管道内水流平均流速,且前后支撑体断面处的平均流速也大于管道内的平均流速,这主要是由于当水流流经支撑体断面和环状缝隙断面时,过水断面面积减小,根据连续性方程A1V1=A2V2可知,当断面面积变小时,流速相应增大,由于环状缝隙断面面积远小于管道断面面积,从而使得环状缝隙流流速增大,前后支撑体断面较管道断面略小而大于环状缝隙断面面积,使得流经前后支撑体断面处的平均流速大于管道内平均流速而小于环状缝隙流平均流速。随着雷诺数的增大,管道内水流平均流速、前后支撑体断面处平均流速以及环状缝隙内水流平均流速均呈现出逐渐增大的变化趋势。这主要是由于随着雷诺数的增大,圆管水流流速也逐渐增大,依据连续性方程,环状缝隙流流速也相应增大。
从图6可以看出:同一雷诺数条件下,管道车车前、车中和车后三个断面的流速分布大致相同,均以管道中心成同心圆分布,即半径相等的圆环上环状缝隙流流速大致相等。从图6还可以看出,对于车前、车中和车后断面而言,靠近管壁和管道车壁面处的流速基本为0,而环状缝隙中部位置处流速较大,即沿管道半径方向,从管道车车壁面到管壁面环状缝隙流流速呈现出先增大后减小的变化趋势。这是因为管道车和圆管固定不动,车身壁面和管壁处的流速为零,同时由于黏性阻力的存在导致靠近管道车车壁和管壁处的水流流速较小,随着离管道车壁面和管道壁面的距离逐渐增大,环状缝隙流所受束缚作用逐渐减小,环状缝隙流流速也逐渐增大,在靠近环状缝隙中央位置处环状缝隙流流速达到最大。
从图6车前、车后支撑体断面的速度分布云图可以看出:前后支撑体断面处水流均呈现同心环状分布,即沿管道半径方向,自管道中心位置向管壁面流速呈现出先增大后减小的变化趋势,且在到达支撑体附近区域时流速值达到最大。这主要是由于支撑体距离管道车端面较近,管道车前后端面对水流起到阻碍作用,使得靠近该区域的水流流速值较低,而由于支撑体顶端与管道壁面存在微小缝隙,水流在流过支撑体顶部时,发生类圆柱体绕流现象,且断面急速收缩流线在此处被急速压缩并发生一定弯折,使得水流速迅速增大。从图6中还能观察到车后支撑体断面流速变化较车前支撑体断面剧烈,且车后支撑体断面在靠近管道壁面附近存在一个水流高速区,而车前支撑体断面在靠近管壁附近流速分布则相对缓和,这主要是由于水流在刚接触车前支撑体而未进入缝隙时流速较小,且在管道中分布较为均匀,在车前支撑体处虽也产生了绕流,但流速变化相对较小;而对于车后支撑体,当水流自环状缝隙流出时,流速已远大于管道内水流平均流速,由于支撑体距离车后断面距离较近,水流还未充分扩散流速也还未变小,所以在接触到车后支撑体且发生绕流时,水流速依然很大,从而使得车后支撑体附近的流速要大于车前支撑体。由此可知,支撑体附近的流场分布变化更加复杂,且支撑体的存在对车前、车后断面以及环状缝隙内的流场分布都起到一定的影响作用,因此加强对支撑体附近流场的研究分析,可为支撑体结构的优化提供一定的理论指导。
为了进一步分析环状缝隙流沿车身的变化规律,选取雷诺数Re2=154 018时的管道纵断面进行研究,如图7所示。

图7 雷诺数Re2=154 018时管道纵断面流速分布云图
图7为管道轴线所在纵断面,从图中可以看出:水流在管道中流动且未到达车前断面时,水流速度相对较小,当水流到达管道车前端时,由于管道车静止不动,对水流起到阻碍作用,端面近壁面处流速减小,水流流入环状缝隙时,在环状缝隙入口处流速突然增大,之后沿车身方向水流流速逐渐降低,当水流接近管道车车后断面位置时,水流流速又稍稍增大,这与上文的分析相一致,通过物理试验也验证了这一结论。水流流出环状缝隙后在车后支撑体处流速又再次增大。当水流离开管道车后,靠近管道壁面的水流流速并未迅速减小到管内平均流速大小,而是沿管道壁面向下游扩散一定距离之后逐渐趋于稳定,最终恢复到管道内平均流速大小。从图7中还可以看出当水流流出环状缝隙后,在距车后端面不远处出现一个流速稍大的圆形区域,这主要是由于水流流出环状缝隙后,部分水流向管道中心位置扩散,同时由于部分水流回流向端面,在靠近管道车端面附近形成漩涡,从局部矢量图中能观测出在车后端面处有上下两个漩涡,上部漩涡成顺时针方向,下部漩涡成逆时针方向,上下漩涡的水流在管道中心位置处相交汇,且速度方向相同均朝向管道车车后端面,进而使得该位置处的水流流速增大;而随着距离管道车端面距离的不断增大,漩涡逐渐消失,管道中心位置处的水流也渐渐恢复到管道内平均流速的大小。
3.2 压强特性分析
为对管道内压强变化进行研究,选取雷诺数Re3=192 522时0°极轴位置处管道纵断面沿程压强分布云图进行分析,如图8所示。

图8 沿程压强分布云图
从图8中可知:管道车上游位置处压强值较大,而管道车车身周围压强值较小,靠近管道车车后断面位置处压强值也较小,而随着距管道车车后断面距离的增加压强值又逐渐增大;同时还发现在环状缝隙入口和车后支撑体附近处出现了负压区。为了更加准确分析沿程压强变化情况,绘制不同雷诺数下沿程压强变化曲线,如图9所示。

Re1=115 513
图9中横坐标为0的位置表示管道车中心位置,0刻度左侧数字表示管道车中心距上游速度入口的距离,0刻度右侧数字表示管道车中心距压力出口的距离。从图9可以看出:① 不同雷诺数条件下,管道内压强值沿程变化的趋势大致相同,即从上游入口处到管道车车前断面压强值较大且沿程逐渐降低,而在管道车车前断面处压强值迅速降低,之后在车后断面处压强值又开始逐渐升高,待压强值增大到一定程度后又沿程逐渐降低,只是降低的幅度较小。这主要是由于在管道车上游位置处水流流速变化较小即动能变化不大,同时由于阻力的存在,造成部分能量的损失,根据能量方程可知,管道内压能也随之降低,即压强值沿程降低;当水流到达环状缝隙后,水流流速急速增大,使得动能瞬间增大,此时压能随之迅速降低,因此压强值在管道车车前断面处突然降低,甚至出现了负压区;当水流流出环状缝隙之后,由于水流扩散导致流速降低,此时压强值开始升高,随着距车后断面距离的增加,水流流速逐渐趋于稳定,压强值也逐渐达到最大,之后由于沿程水头损失,压能逐渐降低,压强值又开始沿程减小。② 随着雷诺数的增大,管道车上游断面、环状缝隙内以及管道车下游断面的压强值均呈现出逐渐增大的趋势,只是上游断面的增加值大于环状缝隙内和下游断面,且环状缝隙内部压强值随雷诺的变化相对较小。同一雷诺数条件下,管道车上游位置处压强值大于下游和环状缝隙内部压强值,这主要是由于管道车在管道内固定不动,对水流起到了拥堵作用,进而使得上游压强值增大;而在环状缝隙内部,压强呈现出现先增大后减小的变化趋势,这主要是由于水流流速在环状缝隙内呈现出先减小后增大的变化趋势,动能也呈现出先减小后增大的变化趋势,进而使得压能呈现先增大后减小的变化趋势。
3.3 涡特性分析
旋涡的存在是造成管道内能耗损失的一个重要原因,同时由于静止管道车车身轴线与水流方向平行,这与传统的圆柱轴线与水流垂直的绕流形式不同,存在区别和差异。因此,通过数值模拟计算,对不同雷诺数下的涡量特性进行分析,其涡量分布云图,如图10所示。
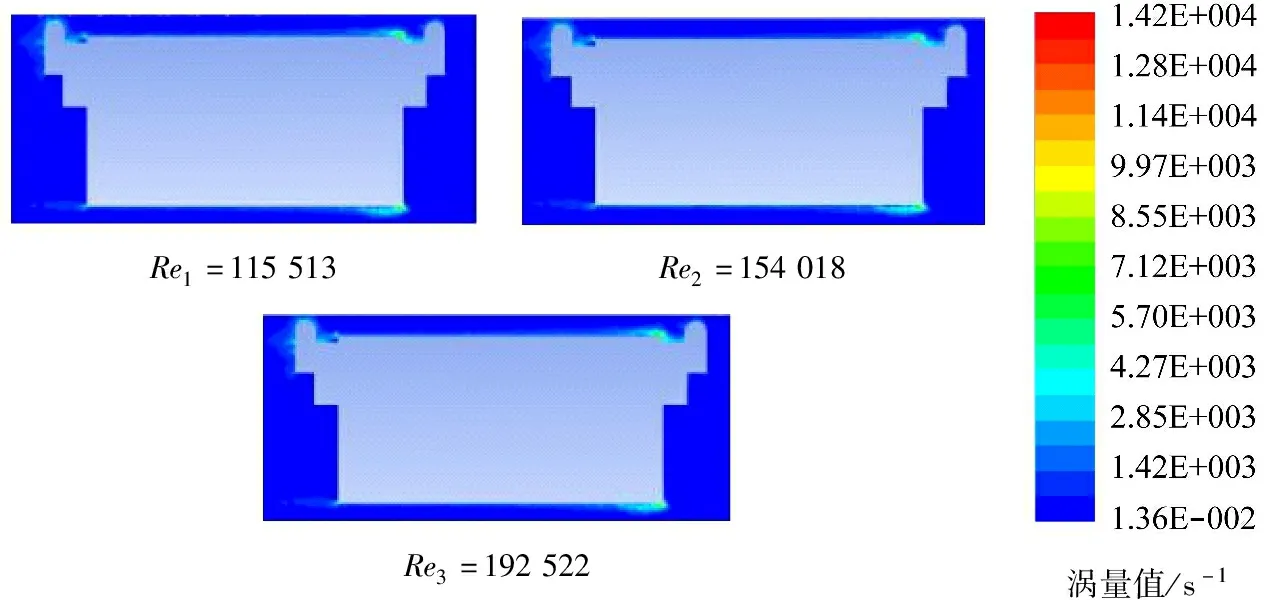
图10 不同雷诺数下0度极轴位置处纵断面涡量分布云图
从图10中可以发现:① 车前与车后断面附近涡量值较高,这主要是由于在环状缝隙进口处发生圆柱绕流,且车前断面收缩变小使得流速迅速增大,其动能也迅速增大,根据能量方程车前断面处压能减小,水流由高压区压向低压区,在车前断面靠近管道车壁面处形成漩涡,由于车前断面流速较大使得水流混掺剧烈程度增大,涡量值也随之增大。而对于车后断面,由于该处断面面积突然扩大,水流流速降低,动能也随之降低,压能随之升高,此处水流被压向低压区,在靠近出口断面的低压区附近水流相互混掺形成漩涡,使得缝隙出口处涡量值变大。前后支撑体附近涡量值也较大,这主要是因为在前后支撑体附近发生经典圆柱体绕流现象,使得该处的水流混掺效果增强,导致涡量增大。② 随着雷诺数的变化,在缝隙进口端和出口端并未观察到明显的脱涡现象,支撑体附近虽然发生了绕流但也未形成脱涡,这主要是由于环状缝隙进出口与管道壁面形成有限封闭区间,限制了涡的发展。③ 随着雷诺数的增大,涡量值也呈现逐渐增大的趋势,这主要是由于雷诺数增大,水流流速相应增大,水流之间的相互混掺变的更加剧烈,能量耗散也增大,相应的涡量值增大。
3.4 数值模拟验证分析
通过对比模型试验和数值模拟结果,验证数值模拟的准确性,选取车前断面0°极轴位置处不同极半径的速度实测值与模拟值进行对比分析,如图11所示。
从图11看出,试验实测值在模拟值上下浮动,通过对数值模拟和试验实测环状缝隙流流速进行计算,得出二者的最大相对误差不超过7%。从图11还可以看出,无论是数值模拟还是模型试验,随着雷诺数增加,同一极半径处环状缝隙流流速也呈现出逐渐增大的变化趋势;当雷诺数一定时,随着极半径的增大,环状缝隙流流速呈现出先增大后减小的变化形式;为进一步探究环状缝隙流的分布规律,对不同雷诺数下环状缝隙流流速模拟结果和实测结果进行公式拟合,如表3所示。

图11 环状缝隙流流速模拟值和实测值对比示意图

表3 环状缝隙流速度拟合
通过表3可知,环状缝隙入口处水流流速分布呈二次抛物线形式,而管道内无管道车时的水流按对数规律分布,两者存在一定的差异。水流在环状缝隙内的流速可分解为三个方向,即沿管道轴线的轴向速度、沿管道横断面圆周切线方向的周向速度以及沿管道半径方向的径向速度,为进一步对数值模拟结果进行验证,选取90°极轴、极半径45 mm位置处,在不同雷诺数下沿管道车车身方向环状缝隙流的轴向、周向和径向流速进行分析,如图12所示。
从图12可以看出,试验实测值和数值模拟值较为接近,两者最大相对误差不超过8%,从而验证了数值模拟的准确性。本试验规定轴向速度沿水流方向为正,周向速度沿测环切线逆时针方向为正,径向速度以背离管道断面圆心方向为正,则从图12(a)可以发现,在同一雷诺数情况下,随着车身长度的增加,环状缝隙流轴向速度呈现出先减小后增大的趋势,且在车前位置处流速最大,这与环状缝隙流流速整体分布大致相同,同时随着雷诺数的增大,环状缝隙流轴向流速也呈现出逐渐增大的趋势,但在不同雷诺数条件下,沿管道车车身方向轴向流速的整体变化趋势大致相同。从图12(b)可以看出,同一雷诺数条件下,径向速度沿车身方向呈现出先减小再增大最后再减小的趋势;径向速度有正负,表明径向速度沿管道半径有指向圆心和背离圆心两个方向;在车前断面径向速度达到最大,且径向速度为正,表明车前断面径向速度背离圆心方向,这主要是由于水流进入环状缝隙时,在车前断面处发生绕流现象,水流在该处被压缩然后挤向管道壁面,从而产生背离管道圆心的径向速度;随着车身长度的增加,径向速度逐渐趋于零,这主要是由于水流进入环状缝隙之后逐渐趋于稳定,流线与管道轴线近乎平行,从而使得沿半径方向的速度分量减小,即径向速度变小。从图12(c)发现,较轴向、径向流速相比,周向速度分布规律性较差沿车身方向变化较为激烈,且周向速度值也较小;周向速度值有正有负,表明周向速度沿断面圆周切线呈顺时针和逆时针两个方向。
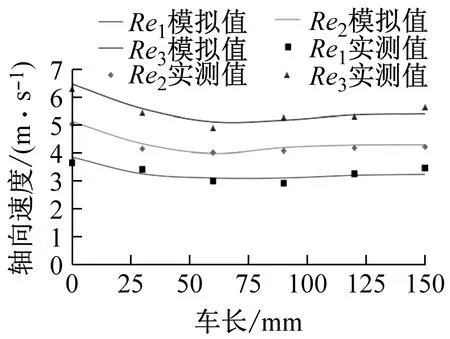
(a)轴向速度
4 结 论
本文通过数值模拟和物理模型验证相结合的方法对不同雷诺数条件下静止管道车环状缝隙流流速特性进行了研究,所得结论如下:
(1)同一雷诺数条件下,车前断面环状缝隙流流速大于车中和车后断面,即沿车身方向,环状缝隙流呈现出先减小后增大的变化趋势;随着雷诺数的增加,车身环状缝隙流速呈现出逐渐增大的变化趋势。
(2)不同雷诺数条件下,管道内压强值沿程变化趋势大致相同,即在上游段压强值沿程降低,在环状缝隙内部压强值沿程先增大后减小,在下游段压强值先增大后逐渐降低;随着雷诺数的增加,管道内压强值也呈现逐渐增大的变化趋势。
(3)车前支撑体附近流速小于车后支撑体,车前和车后支撑体断面流场仍呈同心圆环状分布。车前和车后断面附近涡量值较大,且在支撑体和车后断面处并未观察到脱涡现象,随着雷诺数的增大,涡量值也呈现出逐渐增大的趋势。
(4)环状缝隙流流速成二次抛物线形式分布,且环状缝隙流轴向流速远大于周向和径向流速。
(5)物理模型试验结果与数值模拟结果最大相对误差不超过7%,即通过数值模拟来研究不同雷诺数下的环状缝隙流流速特性是可行的。
通过对静止管道车环状缝隙流场进行研究,进一步丰富管道水力输送理论,同时有助于优化管道车模型结构,而对于管道车静止状态下的压强分布和能量耗散还有待进一步研究。
