相位敏感OTDR和布里渊OTDR结合的双参量分布式光纤传感的研究
2021-02-07李书华王泽义范明华
张 凯,药 炜,原 军,赵 杨,张 坤,陈 冉,李书华,,王 坤,,王泽义,范明华
(1.国网太原供电公司,山西 太原 030012;2.武汉康普常青软件技术股份有限公司,湖北 武汉 430073)
1 引 言
相对于传统的点式传感器,分布式光纤传感器能够实现整条传感光纤上物理量的连续测量,因而分布式光纤传感技术引起国内外的广泛关注。此外分布式光纤传感技术具有测量范围广、结构简单、体积小、抗腐蚀、耐高温、抗电磁干扰以及灵敏度高等优点,在诸多领域得到广泛应用[1-5]。基于布里渊散射和瑞利散射的光时域反射计因其传感原理基于光纤中传输光的布里渊散射光频率和瑞利散射光相位变化,所以其测量精度和灵敏度极高,非常适用于温度/应变和振动事件的检测,可广泛应用于地质灾害监测、长距离大范围温度监测、结构健康监测、通信线路安全监测、输电线路运营监测、周界安防系统监测、油气管道运营安全监测、天然气开采等领域[6-9]。
随着光纤传感技术的发展和应用,多参量监测已成为光纤监控系统的必然发展趋势,为故障事件的综合识别提供了更全面的判断依据和更有效的途径[10]。而基于布里渊散射或瑞利散射的光时域反射计均只能测量单一物理量,如布里渊光时域反射计(BOTDR)只能检测光纤沿线的温度/应变,而相位敏感光时域反射计(Φ-OTDR)只能检测光纤沿线的振动及分布,因此单一设备无法做到满足多参量物理场的监测应用需求。针对该多参量物理场的测量需求,在BOTDR和Φ-OTDR的基础上,本文提出了一种基于分布式光纤传感的多参量测量传感系统,可通过一根光纤实现温度/应变和振动的同时测量,并进行了实验验证得到比较好的测量效果。经验证分析,该系统的测量距离达50 km以上,空间分辨率可达20 m,温度测量精度为±3 ℃,频率测量精度±0.15 Hz以上。
2 基本原理
2.1 BOTDR技术
光纤中布里渊频移υB主要决定于入射光频率υ0、光纤介质折射率n、光纤内声速V等参量[11-12]:
υB=(2υ0/c)nV
(1)
其中,c为真空中光速。当光纤的温度/应变出现变化时,光纤介质的折射率和声速会随之发生相应的变化,使得光纤布里渊中心频率发生改变。通过检测布里渊中心频率的变化量就可获知温度/应变的变化量。
如图1为基于布里渊散射的分布式光纤传感原理图。若z处的入射脉冲光功率为P(z),则距入射端z处的dz小段光纤上产生的后向布里渊散射光功率为[13]:
(2)
其中,αz是光纤衰减系数;g(υ,υB)为布里增益谱[5]:
(3)
其中,w为布里渊增益谱的线宽;g0为布里渊增益谱峰值;υB为布里渊频移,随光纤的温度或应变而变化。布里渊频移与应变或温度的关系为[14]:
υB(ε,T)=υB0+CT·ΔT+Cε·Δε
(4)
其中,υB0为光纤初始温度下无应变的布里渊频移;CT是布里渊频移随温度的变化系数;Cε是布里渊频移随应变的变化系数。依据光时域反射技术测量并记录沿光纤每一点z处的后向散射光的布里渊频移,布里渊光时域反射计即可实现沿光纤各位置点的应变/温度测量。
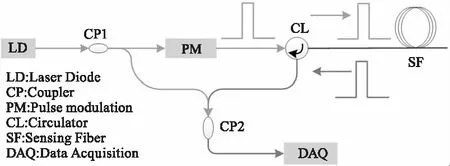
图1 BOTDR系统
2.2 Φ-OTDR技术
相位敏感光时域反射技术(Φ-OTDR)是在光时域反射技术(OTDR)为基础发展起来的。如图2所示,窄线宽激光器输出高度相干的连续光被调制成脉冲光信号,经由环形器进入传感光纤。探测光脉冲在传感光纤中传输的过程中,因为光纤沿轴向的折射率的分布的不均匀性,产生瑞利散射光,其中背向瑞利散射光通过环形器输出到信号采集单元。
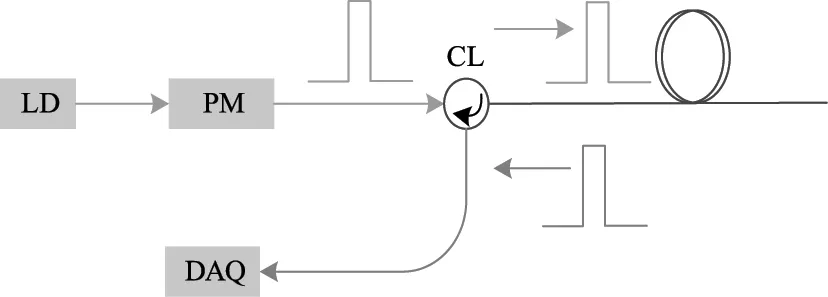
图2 Φ-OTDR系统
当有传感光纤上振动发生时,瑞利散射信号会受到相位调制。在振动区域的瑞利散射信号受到的相位调制互不相同,使得信号的幅度产生变化,通过检测及分析这种变化就可以探测到振动事件的发生[15]。Φ-OTDR曲线的幅度受到光纤折射率分布的影响,具有随机性,但没有外界扰动时,是较为稳定的。当发生振动时,振动位置散射信号的幅度发生变化[16]。所以观察检测到的后向散射曲线的时间差分,就可看出振动信号的位置。
2.3 双参量监测系统
传感应用中,BOTDR系统只能监测光纤沿线的应变/温度,而Φ-OTDR只能监测光纤沿线的振动信息。同时相位敏感光时域反射计(Φ-OTDR)和布里渊光时域反射计(BOTDR)的基础均为光时域反射(OTDR)技术,不同之处在于检测的信号有区别,即瑞利散射信号和布里渊散射信号。本文所设计的双参量分布式光纤传感系统采用窄线宽脉冲光源产生布里渊散射信号和瑞利散射信号,并通过耦合器分离光纤中散射信号并分别检测,具体原理图如图3所示。其中利用相干检测方式来检测光纤中的布里渊散射信号;由于光纤中的布里渊散射信号强度较瑞利散射信号弱3个数量级左右,可以忽略布里渊散射信号强度对瑞利散射信号的影响。因此采用直接检测的方式检测瑞利散射信号的强度变化。即该系统通过同时测量光纤中的瑞利散射和布里渊散射信号,在一根传感光纤中实现了温度/应变和振动的双参量检测。
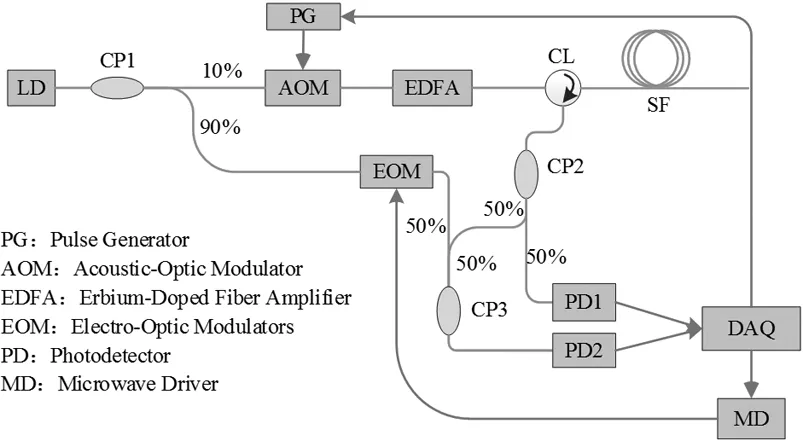
图3 双参量分布式光纤传感系统
3 分析与讨论
3.1 实验装置
图3中所示的双参量传感系统主要由以下几部分组成:窄线宽光源输出连续光经过1×2耦合器(Coupler 1)分为两路,一路经声光调制器(AOM)调制成脉冲后经过光脉冲放大器(EDFA)进入光纤作为探测信号,另一路作为参考信号。参考信号经电光调制器(EOM)调频,接着通过扰偏器(PS)作用及单边带滤波器(Filter)后进入耦合器(Coupler 3)。探测信号在光纤中与其作用产生瑞利散射及布里渊散射信号,散射信号通过环形器(Circulator)三端口输出到1×2耦合器(Coupler 2)。其中耦合器2的一个输出信号输出到耦合器3并与参考信号混频得到包含位置信息的差频信号,通过解析得到光纤沿线的应变/温度信息。耦合器2的另一路信号直接被探测器(PD2)接收和采集,进行光纤沿线振动信息分析。
DAQ最大采样速率为100 MHz,双通道采集,分别对应布里渊差频信号和瑞利散射信号。其中布里渊散射信号采集设置50 MHz,瑞利散射信号采集设置12.5 MHz。经过DAQ采样后,对布里渊差频信号数据进行洛伦兹拟合(Lorentz fitting),通过拟合的结果可以得到布里渊散射信号中心频率(Brillouin center frequency)。进而可以分析得到光纤沿线的温度/应变分布;对瑞利散射信号中进行傅里叶变换(parallel Fourier transform)分析,得到光纤沿线的振动及幅度大小分布。实现温度/应变和振动的多参量测量。
本文通过集成BOTDR和Φ-OTDR,由单个系统实现双参量分析解调和监测的分布式光纤传感探测系统。
3.2 实验结果分析
为了验证系统能进行双参量测量和分析,根据双参量分布式光纤探测系统方案和结构搭建了样机系统及测试方案。如图4所示,实验中通过恒温水浴槽和压电陶瓷管(PZT)同时给同一条传感光纤的不同位置分别加载温度和振动信号,系统采集散射信号并交由上位机软件分析。传感光纤的总长度为50 km,将50 km末端的一段光纤(约20 m)绕成光纤环并放置于恒温水浴槽中进行温度测试;在光纤45 km附近的位置接入PZT振动模块进行振动频率测试及分析。得到温度曲线及其线性曲线、频率曲线及其线性曲线分别如图5~8所示。
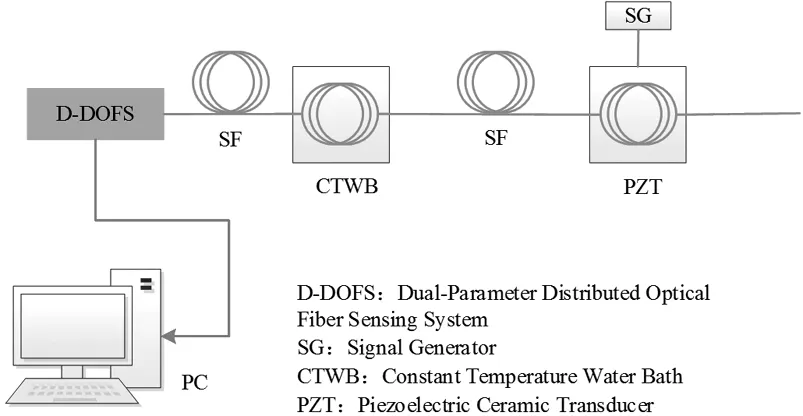
图4 性能测试方案
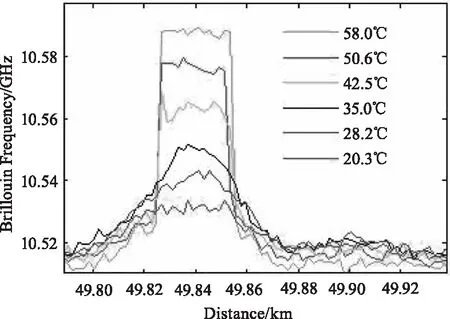
图5 不同温度下测量效果
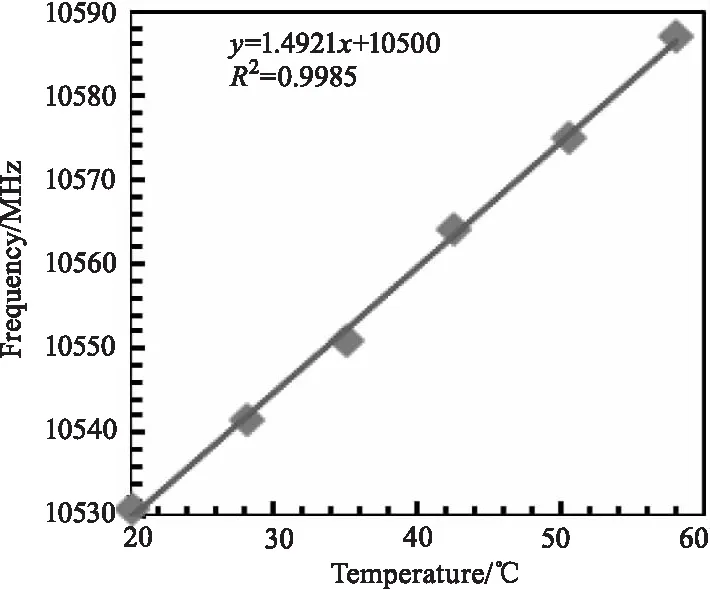
图6 温度拟合曲线图
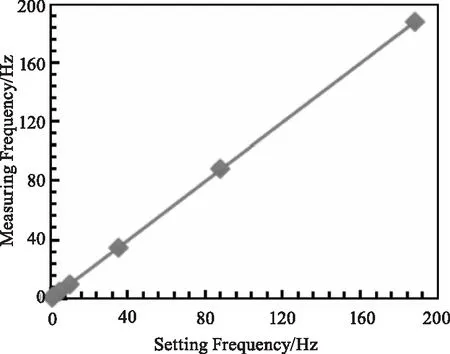
图7 PZT设定值和测量值拟合曲线
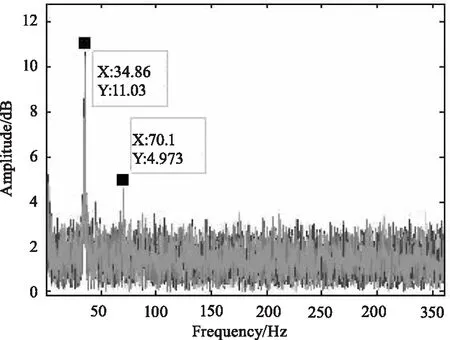
图8 PZT设定35Hz多次测量效果
3.2.1 温度测量效果分析
将采集到的布里渊散射信号数据利用洛伦兹最小二乘法进行拟合,分别得到光纤沿线各位置点的布里渊中心频率。
将50 km传感光纤末端20 m左右段置于恒温水浴槽中,分别加热至20.3 ℃,28.2 ℃,35.0 ℃,42.5 ℃,50.6 ℃,58.0 ℃,得到其不同温度对应的布里渊谱中心频率值,图5为检测结果。实验中采用多次累加平均去噪方式,减小其他因素的扰动引起的测量误差,提高系统测量精度和信噪比。对数据进行线性拟合如图6所示,可以看到设置温度与获得的布里渊散射中心频率之间具有良好的线性关系,曲线的斜率为1.492 MHz·℃-1,线性度为0.9985。
3.2.2 振动频率测量效果分析
对采集的振动数据进行频域分析,通过FFT变换,在一定时间尺度上对光纤上每一点的数据进行FFT分析,得到各位置点的频域数据。如图7所示,设定PZT频率值为1 Hz,2 Hz,5 Hz,10 Hz,35 Hz,88 Hz,188 Hz,分析测量数据得到相应的振动频率值分别为1.027 Hz,1.85 Hz,5.01 Hz,10.01 Hz,34.86 Hz,88.09 Hz,188.05 Hz,线性拟合对比,其拟合斜率为1。该系统能准确感测光纤沿线振动频率大小,并定位。
图8是对同一频率(35 Hz)设定值进行多次测量的分析结果,由图8可知,多次测量得到的分析结果稳定,在70Hz处有一个倍频信号,其测量误差为0.4 %@35 Hz。
由实验测试结果可知:①在200 ns脉冲宽度下,系统测量距离可达50 km以上;② 系统空间分辨率可达20 m;③温度测量精度为±3 ℃,振动频率测量范围为1~750 Hz@50 km,频率测量精度为±0.15 Hz(与采样频率有关);④系统的温度测量线性度较好,可达0.9985。
3.3 监测参量交叉敏感实验及分析
该系统在一根光纤中实现了温度/应变和振动等参量的同时监测和解析。根据系统原理,其所检测的两个参量分别由不同的散射信号(即布里渊散射信号和瑞利散射信号)解析得到。基于前文的分析,从信号解析的角度,瑞利散射信号强度较布里渊散射信号高出3个数量级左右,因此在瑞利散射信号的检测中可以忽略布里渊散射信号的影响。同时,对布里渊散射信号的检测是采用相干检测的方式,该检测方案可以直接过滤瑞利散射信号,即排除了瑞利散射信号对布里渊散射信号的干扰;从基本原理角度,BOTDR和Φ-OTDR都是由外界信号对光纤折射率的调制而加载信息到布里渊散射信号和瑞利散射信号上,通过对不同信号的解析来分析得到外界参量的变化。所不同的是,外界参量的变化速率及对折射率调制的速率。下面通过实验及分析验证该系统的监测参量的交叉敏感性能。
3.3.1 温度/应变对振动测量的影响
实际测量及应用场景中,对振动的测量在数秒甚至更少时间内即可完成,温度和应变的变化是较缓慢的,可以当作静止状态来处理。也就是说温度和应变对振动的影响可以忽略不计。
对于快速的应变变化,如果是周期性的,可以转换为振动参量进行振动频率测量和振幅测量,根据频率和振幅来定性分析应变变化趋势。如果测量光纤长度不大于2 km,可通过设置测量参数实现温度/应变的快速测量,进而分析其变化频率。根据系统性能情况,其应变测量频率为0 Hz~10 Hz。
3.3.2 振动对温度/应变测量的影响
一般振动为连续的周期性的变化,通过对光纤的作用将振动信息加载到瑞利散射信号上。其周期大小跟振动频率直接相关。
而温度/应变参量的测量是基于光纤布里渊频移的,其单次测量时间较长,为几十秒至几十分钟不等,远大于单次振动参量测量时间。为研究光纤振动对温度/应变(即布里渊散射频移)的影响,设计以下实验,具体测试方案如图9所示。
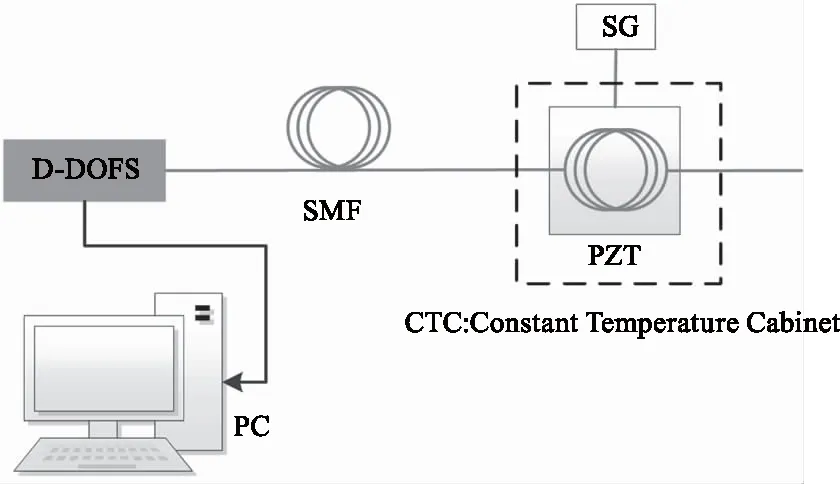
图9 双参量交叉敏感试验方案
根据图9所示的测试方案,测量系统接入30 km传感光纤,并在光纤末端串接40 m左右长度的光纤,其中20 m光纤紧密缠绕于PZT上。将PZT置于恒温箱内,设置恒温箱的温度稳定为(24 ±1 ℃)。为保证信号质量,提高信噪比,设置叠加次数为4096,扫频范围跨度200 MHz,步距5 MHz,则其单次测量时间约为60 s。测试过程中,通过信号发生器给PZT加载振动信号,振动频率范围为0.1 Hz~1 MHz。观察分析振动信号对布里渊频移的影响。具体测试效果如图10和图11所示。尾端串接光纤布里渊频率约为10.272 GHz,其前端20 m左右光纤由于缠绕在压电陶瓷管上而出现一定应变效果,使得该段光纤布里渊频率变为10.415 GHz左右。测试过程中设置信号发生器输出不同频率的正弦信号,振幅为0.5 V。由图10可知,在没有加载振动及加载不同的振动频率振动情况下,该区段光纤布里渊散射频率在10.411 GHz~10.417 GHz范围内变化,即频率变化幅度为±4 MHz,结合温控箱的控温精度误差,可知该测量结果处于系统测量精度范围内。也即是说振动不影响光纤布里渊频率的测量,也不影响其温度/应变的测量。图11展示了测试光纤段的布里渊频率与振动频率的关系。曲线显示,在恒温环境下,给光纤段加载不同振动频率,其布里渊频率并不随着振动频率而变化,处于随机波动,波动范围小于±4 MHz。
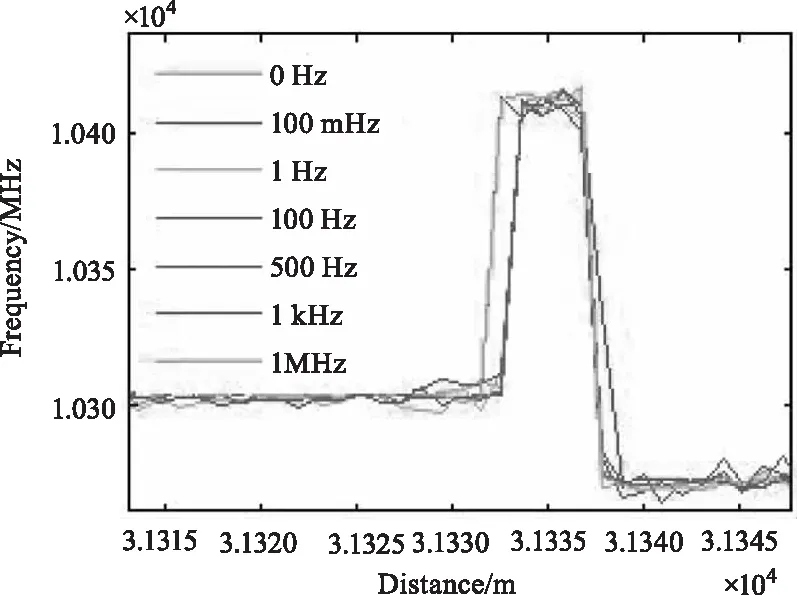
图10 不同振动频率下测试光纤段的布里渊频移
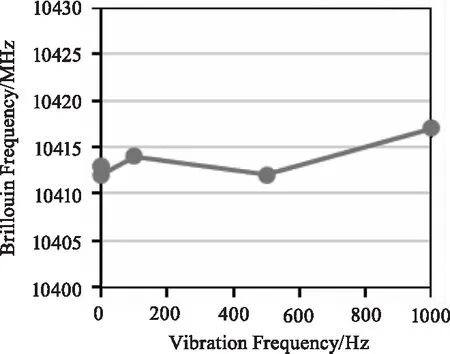
图11 PZT设定35 Hz多次测量效果
根据以上实验及分析可以得到,温度/应变一般为缓慢的变换,相对于一般频率(0.1 Hz~1 MHz)的振动来说,处于静止状态,因此不会影响振动的测量;同时振动为连续的周期性的快速变化,亦不会影响温度/应变的测量。即在实际应用场景中,温度/应变和振动参量不会交叉敏感。
4 结 论
本文通过分析BOTDR和相位OTDR技术,综合其分布式光纤传感技术优势,提出了一种多参量同时测量的分布式光纤传感方案,将原来需要多套系统实现的传感方案改进为单个系统即可实现。降低了传感系统的结构及应用成本,拓展了应用市场领域。实验结果表明,多参量分布式光纤传感系统可实现应变/温度和振动信号的测量,不会产生温度/应变与振动监测参量的交叉敏感问题。且达到测量距离50 km,空间分辨率20 m,温度精度±3 ℃,频率测量精度±0.15 Hz的测量效果。
