烟幕扩散模型中任意光路电磁波透过率的计算

蒋 云,李 伟,宋伟伟,于照亮,代晓东

(防化研究院,北京 102205)

1 引 言

烟幕是现代战争中对抗精确制导武器和光电观瞄器材的有效手段,能够遮蔽干扰可见光、激光、红外、毫米波等电磁波,具有使用方便、效费比高等特点,受到世界军事强国的重视[1-3]。烟幕能够对波段电磁波形成有效干扰的关键因素在于:首先,烟幕中含有大量能够对电磁波产生散射或吸收效果的烟幕粒子；其次,烟幕粒子能够在大气中通过扩散形成足够浓度和尺寸的烟幕云团,在制导武器和保护目标之间形成有效屏障[4-6]。在烟幕技术领域,烟幕粒子扩散特性的研究一直是一个难点和热点,人们利用各种计算模型对烟幕云团的扩散特性进行计算和模拟,高斯扩散模型和随机游走模型是该领域最常用的两个计算模型[7-8]。特别是随机游走模型,它基于拉格朗日算法,不受平衡和均匀假设的限制,扩散过程与时间相关,具有广泛的适用性[9-10]。在随机游走模型中,输入烟幕施放源参数、风场参数、温度场参数以及其他相关参数,可以较为准确的模拟出烟幕的扩散尺寸以及浓度分布情况。电磁波会从任何可能的方向穿过烟幕云团,在计算模拟中需要准确得到烟幕云团沿任意路径的浓度变化情况,从而计算出电磁波沿这一路径穿过云团时的透过率,得到烟幕云团对电磁波的衰减效果。文献中关于随机游走模型本身的介绍较多,在实现任意方向和角度的计算和分析方面,目前没有公开可见的报道。本文基于空间几何坐标变换原理、线性代数矩阵运算方法以及烟幕材料消光理论,推导了烟幕扩散模型中电磁波入射方向改变时的坐标系变换矩阵、积分浓度及透过率计算公式,为烟幕扩散模型的多角度(方向)数据分析、烟幕云团图像处理以及更多应用场景中的使用奠定了基础。

2 透过率的计算

在烟幕随机游走模型中,需要构建一个长方体形状的计算区域,烟幕施放点设为坐标原点,施放出的所有烟幕粒子都在该计算区域里扩散运动,通过随机扩散模型可模拟烟幕粒子在该三维空间中的分布情况。计算模拟时一般将计算区域被划分为若干网格,设坐标轴x、y、z三个方向的网格精细度分别为Δx、Δy和Δz,则每个长方体小网格中的浓度可由式(1)计算得到[11]:

(1)

其中,C(i,t)为第i个网格在t时刻的质量浓度;Q(t)为t时刻施放的烟幕粒子总质量;ni(t)为t时刻第i个网格中的烟幕粒子数量;N为总的烟幕粒子数量。根据朗伯-比尔定律[12-13],电磁波经过第i个网格的透过率Ti可表达为:

Ti=e-c(i,t)·ΔLi·α

(2)

其中,α为烟幕的质量消光系数;ΔLi为电磁波经过第i个网格时的光程。

如果电磁波入射方向与任意一个坐标轴方向平行,则很容易知道其经过每个网格的光程。例如电磁波沿x轴穿过烟幕云团,则经过每个网格的光程均为Δx,设x轴方向的网格数量为m,电磁波的初始能量为I0,则电磁波经过第一个网格后的能量I1为I0·T1,经过第二个网格后的能量I2为I0·T1·T2,以此类推,经过第m个网格后的能量Im为I0·T1·T2…Tm。因此一束电磁波沿x轴经过整个烟幕云团的透过率Tx为:

(3)

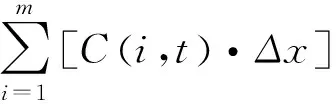
Tx=e-α·Cx

(4)

显然,只要知道了沿空间某一路径L的积分浓度CL,就可以根据式(4)得到电磁波经过该路径后的透过率TL。

当电磁波沿任意方向入射时,无法准确知道电磁波穿过每个网格时的路径长度ΔL,从而无法准确计算积分浓度。特别是把烟幕模型嵌入一个更大的视场中时,烟幕模型中的坐标只是相对坐标,无法根据该坐标系的坐标值进行积分浓度的准确计算,无法获知任意方向入射的电磁波经过该烟幕云团时发生的衰减情况。烟幕扩散模型中任意光路下积分浓度的计算和分析,以及该模型嵌入其他应用场景中,均涉及到空间坐标系的变换。

3 三维坐标系的转换

实现任意光路积分浓度计算的基本思路是:建立一个新的空间几何坐标系O′(X′Y′Z′),其原点O′(0,0,0)与原坐标系的原点O(0,0,0)重合,X′轴的方向为电磁波入射方向；得到两个坐标系之间的转换关系,使烟幕模型的空间坐标可以在两个坐标系之间自由转换；将烟幕云团的空间坐标由O(XYZ)坐标系转换到O′(X′Y′Z′)坐标系,然后可以计算得到烟幕在X′方向上的积分浓度分布和电磁波穿过烟幕云团的透过率。

3.1 三维坐标系的建立

新坐标系O′(X′Y′Z′)与原坐标系O(XYZ)的关系如图1所示,两个坐标系均为右手坐标系。图中,X轴的正向为风向,Z的正向为地面的法线方向,XOY平面为水平面,OR为电磁波入射方向(也是新三维坐标系的X′轴),OR′为OR在XOY面上的投影。α角为OR与OR′的夹角,β角为OR′与X轴的夹角。根据地理关系,也可以把α角称为俯仰角(0°～90°),β角称为方位角(0°～360°)。

图1 新三维坐标系与原三维坐标系的关系

3.2 空间坐标系转换矩阵

要实现原坐标系O(XYZ)和新坐标系O′(X′Y′Z′)之间的转换,需要求得它们之间的转换矩阵,包括原坐标系到新坐标系的转换矩阵M以及新坐标系到原坐标系的转换矩阵M′。

(1)M的推导

M的推导方法是:X′轴经过两次旋转操作,与X轴重合,得到原坐标系到新坐标系的转换矩阵M。右手坐标系中绕坐标轴的旋转操作均遵循右手法则,即右手拇指指向旋转轴正向,其余四指的指向便是旋转角的正方向[14]。

第一次旋转操作:OR(即X′轴)绕Y′轴旋转α角度,使OR与OR′重合,其转换矩阵为:

(5)

旋转后得到坐标系O″(X″,Y″,Z″),其X″轴为OR′,Y″轴为OY′,Z″轴为过O(0,0,0)点垂直于X″O″Y″平面的方向。

第二次旋转操作:OR′绕Z″轴旋转(-β)角度,使OR′与X轴重合,其转换矩阵为:

(6)

整个过程的转换矩阵为:

M=My·Mz

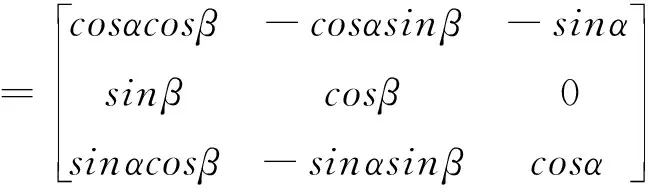
(7)

利用转换矩阵M,可以实现原坐标系中任意一点(x,y,z)到新坐标系的转换,即

(8)

(2)M′的推导

M′推导过程是M的逆过程,操作方法是:X轴经过两次旋转操作,与X′重合,得到新坐标系到原坐标系的转换矩阵M′。

第一次旋转操作:X轴绕Z轴旋转β角度到OR′,其转换矩阵为:

(9)

旋转后得到坐标系O1(X1Y1Z1),其X1轴为OR′,Z1轴为OZ,Y1轴为过O(0,0,0)点垂直于X1O1Z1平面的方向。

第二次旋转操作:OR′绕Y1轴旋转(-α)角度,使OR′与OR重合,其转换矩阵为:

(10)

经过两次旋转,完成了X轴到OR轴的变换,整个过程的转换矩阵为:

(11)

(12)

(3)转换坐标系原点不重合的情况

有时将烟幕扩散模型嵌入另外一个场景中,此时两个转换坐标系的原点不重合,设原坐标系的原点O在新坐标系中的值为(a,b,c),则原坐标系中的任意一点(x,y,z)在新坐标系中可表示为:

(13)

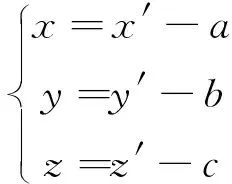
(14)

4 烟幕积分浓度分布计算

4.1 二维坐标系

以三维坐标系O′(x′y′z′)的X′轴为投影方向,Y′O′Z′平面为投影幕,可以得到如图2所示烟幕云团二维投影坐标系,求得二维坐标系中每点的烟幕积分浓度,则得到烟幕云团在X′轴方向的积分浓度二维分布图,进而可以计算电磁波经过二维投影图中任意一点的透过率。

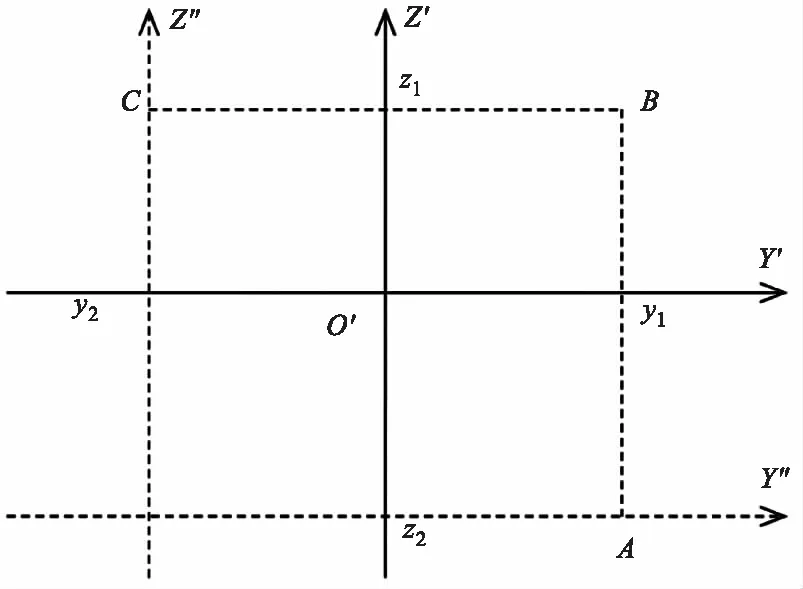
图2 烟幕二维视场坐标系

烟幕云团所在的三维空间投影到Y′O′Z′平面,在Y′轴上的最大值和最小值分别为y1和y2,在Z′轴上的最大值和最小值分别为z1和z2,因此烟幕的投影区域为矩形O″ABC所包含的区域。投影区域的四个顶点O″、A、B、C的坐标分别为(y2,z2)、(y1,z2)、(y1,z1)和(y2,z1)。将坐标系原点O′平移到O″,两个坐标系之间的转换关系为:

(15)

4.2 烟幕积分浓度和透过率的计算

在投影区域内任意一点(y″,z″)上烟幕的积分浓度为:

(16)

其中,x1和x2分别为烟幕体在X′轴方向的最小值和最大值,Δx为X′轴方向的计算精度,y′、z′与y″、z″的关系为:

(17)

(x′,y′,z′)在原坐标系对应的点为(x0,y0,z0),根据式(8)可得:

(18)

从而得到:

C(x′,y′,z′)=C(x0,y0,z0)

(19)

根据朗伯-比尔定律,电磁波沿X′轴方向经过点(x′,y′,z′)的透过率T为:

(20)

5 总 结

通过以上推导,得到了烟幕随机游走模型中三维坐标系的转换矩阵,通过转换矩阵可以很方便地实现新旧坐标系之间的坐标变换,计算烟幕云团沿任意路径的积分浓度和电磁波衰减率。同时,推导了烟幕积分浓度的二维投影算法,可计算出任意投影面上的积分浓度分布情况和电磁波透过该点的透过率,为烟幕扩散模型在多角度数据分析、烟幕云团红外图像处理、更多场景中的应用奠定了基础。