多普勒激光雷达风场反演研究进展

左金辉,贾豫东

(北京信息科技大学仪器科学与光电工程学院,北京 100192)

1 引 言

大气风场探测对生产生活和科学研究具有重要的意义,如何高精度、实时性获取大气风场的各个参数成为大气风场研究的工作之一。传统的大气风场的探测手段有无线电探空仪、天气微波雷达、多普勒声雷达、风廓线雷达等,但传统的探测手段已经无法满足复杂的大气条件、小型化、实时性和高精度等综合性的应用需求。多普勒激光雷达具有高精度测量、高空分辨率、探测范围广、响应速度快的特点[1],在晴空天气的大气探测中具有显著的作用。但通过多普勒激光雷达只能获得一系列的径向风速,必须通过风场反演技术获取风场结构。多普勒激光雷达风场探测模式和反演方法主要源于微波天气雷达,在此基础上进行一系列的改进及创新。通过回顾多普勒激光雷达风场反演技术的发展史,介绍了主要相关算法的研究进展以及优缺点等相关内容。

2 单部多普勒激光雷达风场反演研究

单部激光雷达的径向速度资料只提供风矢量的一个分量的信息,不足以产生水平或三维风场的分析。为弥补单部激光雷达测速观测信息的不足,必须增加更多的信息或者是在反演时施加约束。主要分为两类方法,一是增加信息的方法,二是施加动力约束的方法。

第一类方法中主要从观测量的空间变化(多点观测)和时间演变(多时次观测)方面获取额外的信息,这类方法进行风场反演时往往也需要施加一些约束。主要在微波雷达风场反演方法的基础上进行发展和创新,空间演变的典型的方法有速度方位显示(Velocity Azimuth Display,VAD)、速度方位处理(Velocity Azimuth Processing,VAP)等,时间演变的典型方法是各种平流反演技术。

在观测量的空间变化方面,1961年Lhermitter[2]等在均匀风场假设的下提出的VAD方法在线性风场假设下进一步完善,提高了反演算法的有效性。2000年,VAD算法广泛用于气象业务,成为美国天气雷达(Weather Surveillance Radar-88 Doppler,WSR-88D)的一种主要算法。但一些情况下风场假设的前提并不能很好的成立,风场呈非线性变化时反演实际风场会出现较大的偏差。随激光雷达的应用,基于单部多普勒激光雷达的均匀风场假设下的VAD风场反演方法在业界得到较广泛的应用,早期的VAD方法在方位角的扫描范围和径向分量的个数等方面的要求对激光雷达的反演有一定程度上的影响。针对上述问题在早期微波雷达方面相关人员对VAD风场反演的求解方法上进行部分研究,后Holleman等人[3]研究表明VAD的傅里叶级数的求解方法对多普勒激光雷达的约束较高,从而降低其风场的监测能力；另一方面,Levenber-Marquardt最小二乘法、Newton-Gaussian最小二乘法等非线性最小二乘法的提出及在多普勒激光雷达上的应用证明了该方法的有效性,但Levenber-Marquardt算法对初始值敏感、Newton-Gaussian算法的一阶偏导矩阵不满秩等特征都导致误差增大,限制了多普勒激光雷达高精度、高分辨率条件的满足。针对上述状况提出了梯度下降算法反演、序列二次规划法(Sequence Quadratic Program,SQP)的滤波正弦波拟合(Filter Sine Wave Fitting,FSWF)反演、共轭梯度算法等在保证激光雷达系统的测量性能的同时为动态风场的监测能力提供了更佳的选择。

20世纪70年代后期出现的空间呈线性分布假设下的体速度处理方法(Volume Velocity Processing,VVP),较VAD方法可反演三维风场。较大的分析体积导致VVP算法的运算量增加,同时复杂的矩阵运算和病态矩阵的解算问题都将导致VVP算法反演的误差增加,无法满足激光雷达风场反演的需求。早期研究发现,算法的病态矩阵问题是影响风场反演精度的主要原因。病态矩阵问题作为线性方程组系数矩阵的固有问题,无法将该问题完全解决进而得到准确结果。微波雷达的研究表明,不针对原有的病态线性方程组直接反演风场,而是做一定的改变就有机会减小病态矩阵解算问题所带来的误差。早期仅仅分析系数矩阵的特点,降低方程矩阵的条件数,减小求解难度；避开原始病态方程组直接求解的设想下对VVP算法分布求解的分步的体速度处理[4](Step Volume Velocity Processing,SVVP)方法提出,减小了病态矩阵影响,克服误差放大的问题,进一步证明了SVVP算法的有效性；郎需兴等[5]提出一种新的速度体积处理方法,在分析体积内风场均匀的条件下由变分思想求出水平切向风速,能够反演中尺度风场,该思路进一步在多普勒激光雷达中进行不断改进,以满足反演需求。周生辉等[6]选取主要参量进行反演,引入随机误差、改变模拟风速确定了算法的适用范围；同时VVP算法通过减少部分待求参量的条件下能提高反演精度,并在特定天气情况下进行了实验验证。

80年代后期,我国逐步开展对多普勒激光雷达的风场反演的研究。基于同一距离圈上相邻方位角的风矢量相等的假设下,陶祖钰[7]提出了VAP技术反演二维风场,主要适用于风场变化不太大的情况。VAP反演算法以计算量小、运算简便、效率高等优势在均匀风场反演中广泛受到欢迎,并可以作为大气动力学反演中的初始场。进一步研究表明,当两个相邻径向速度之间的夹角很小时,风速与风向的反演误差很大,甚至超出规定范围,且对含有风切变与较强风向的风场,假设条件不能很好的满足不能进行很好的反演。白洁等人[8]利用二维滤波的方法对原始雷达资料进行预处理,有效的减少了计算误差。随着多普勒激光雷达的的发展,针对VAP算法假设过于理想化的问题,扩展的速度方位处理方法(Extended-VAP,EVAP)[9]的“风速恒定,风向均匀变化”假定提出使其具有反演线性风场的能力,提高反演精度,更好的反演涡旋区域的风场,对机场等特定区域有重要的作用；2011年,罗昌荣对比VAP和EVAP的不足提出VAP方法的扩展应用(EVAP for Tropical Cyclone,EVAPTC)[10]用来更好的反演热带气象近中心风场。VAP的改进主要是基于不同的应用场景,进行不同的前提假设,具有一定的针对性。

观测量的时间演变方面,认为反射粒子在随风漂移的过程中保持守恒。Gal-Chen等[11]提出了平流反演技术,在反射率因子具有Lagrangian守恒性和大气风场的涡度守恒的假设之下,利用多时次体扫获取的原始雷达资料(径向风速和反射率因子)进行三维风场的反演。研究表明,利用运动坐标系进行反演计算,连续性假定无需验证,改善了反演效果。与此同时,在流体不可压缩与冻结湍流的条件下Shapiro等[12]利用双标量法反演行星边界层的三维风场。以上两种非伴随反演技术既使用了诊断分析又有反射率守恒方程和某些附加条件的约束,但假设条件过于严苛。之后对恶劣天气利用参考运动坐标的单多普勒风场反演对平流反演技术进一步完善。

由上述研究可以看出单部多普勒激光雷达风场反演方法的第一类方法中,往往也需要添加一些约束,约束条件的恰当与否则是反演效果和运算量的关键。若要在业务上使用激光雷达的径向风速资料进行反演,更要保证运算量小、精度高、简单适用等条件。所以在不同的条件下,选择不同的约束条件也是尤为重要。这类约束最简单的就是对风场的空间变化做一定的限制,此类限制在实际风场中往往不能总是满足。更有效的是引入大气动力约束,就是在反演时考虑大气运动所要遵循的动力方程。

第二类方法主要是施加大气动力约束,进行风场反演,其中全伴随方法是这类方法的典型。早期基于大气动力学特征提出的涡度与散度的近似表达式,利用傅氏变换的方法进行切向风分量的求解。但符合此模式的观测资料太少,只能应用于理论研究。姜海燕等[13]提出涡度-散度法,应用在微波雷达上利用简化的垂直涡度方程反演水平风场。实验研究表明,该方法反演出的二维风场对于回波单体分裂和演变机制有很好的论证,但方程组本身适用于大尺度系统,使得中尺度风场的反演具有一定的误差。涡度-散度法对小尺度的系统有较好的描述可反映风场的微细的结构但会使得大气中的辐散幅度和涡度进一步增大。之后,葛润生等人在连续方程的约束下进行三维风场的反演,该方案的可行性为今后利用涡度-散度法进行三维风场反演提供了依据,可进一步完善研究和发展。在此基础上引入到多普勒激光雷达的使用,进行了理想模式下低空三维风场反演的研究,表明涡度-散度法可以较好的反映小尺度风场的结构,为今后实际的业务应用提供了依据；之后蒋立辉等[14]首次结合集合卡尔曼滤波同化方法(Ensemble Kalman filtering assimilation,EnKF)和涡度散度方法,EnKF将瞬息万变的大气背景场因素考虑进来后利用涡度-散度方法进行反演,提高了反演的实时性。

1991年,Sun等人提出四维变分同化的方法(全伴随方法)[15]通过连续时间内的雷达信号(径向速度与反射率)的变化信息结合模式共轭方程组反向积分和共轭梯度计算法进行多次迭代,反演三维风场,该算法仅对预报模式做了简化为同化方法的使用提供了基础。在四维变分同化方法的基础上,吴绍荣等[16]提出平面同化反演方法(Plane Assimilation Retrieval,PAR),通过简化垂直方向上的物理量,变为平面位置显示(Plane Position Indicator,PPI)平面上的二维情况,但边界条件的选取确是相当困难。

邱崇践等采用简单伴随函数的方法[17],利用回波强度水平对流方程或者径向风动量方程反演风场结构,大大简化了预报方程,减小了运算量。利用最优控制方法,将一个方程作为控制方程,切向速度、垂直速度等非观测的量值作为该控制方程中的控制变量,利用迭代法进行优化。相关研究表明:(1)使用多时次的原始雷达资料,提高了反演的精确度,降低对观测误差的敏感性,但多时次原始资料中的数据量庞大,计算量明显增加；(2)忽略弱散度和涡度的影响,抑制了数据噪声导致的虚假细微结构；(3)目标函数的系数对反演结果有很大的影响,合适的系数可明显改善反演效果,反之则会偏离正常值。为选择最优的系数,在搜索过程中的计算量较大,今后借助计算机技术的发展,使得该技术进一步发展成为可能。目前,变分同化系统主要基于Sun建立的单多普勒参数反演系统[15],由三部分组成:预报模式、伴随模式、优化方法。

在此基础上对多普勒激光雷达变分同化风场反演进行了研究,Newsom等[18]将多普勒激光雷达四维变分同化(Four-Dimensional Variational Data Assimilation Retrieval,4DVAR)应用到大气边界层模式,并考察了4DVAR算法同化激光雷达资料的性能；之后,Qiu[19]提出三维变分同化(Three-Dimensional Variational Data Assimilation Retrieval,3DVAR)分为两步,第一步是在低阶谱空间反演一个光滑的三维风场作为背景场,第二步在格点上反演风场的细致结构,同时利用了空间变化的约束和时间演变的信息综合考虑了各种约束信息和吸收各种可能的信息,并证明了该算法的有效性；Sun等[15]提出变分多普勒分析系统(Variational Doppler Radar Analysis System,VDRAS)将边界层模式扩展为“湿”模式,不仅获取三维风场也同时获取温度场及微物理场的反演。背景场能改善与弥补资料缺损对同化反演的影响,2010年王改利等[1]人利用4DVAR与3DVAR算法利用多普勒激光雷达对近海面风场资料进行反演,表明将浮标资料为背景场资料的4DVAR算法较优于3DVAR算法,为海面风场反演提供了依据；李勇等[20]人根据平滑罚函数中的平滑罚因子可以改善最小化问题并加速收敛,研究了其在变分同化中的作用表明将平滑罚因子至代价函数提高了风场数据反演的灵敏度,对于小尺度结构时间罚平滑函数较空间罚平滑函数影响不大。

通过上述研究可以发现,变分方法不仅可以得到高精度的风场反演结果,还能获取其他气象参量(气压、温度、热力场等)更加适合业务上的应用。变分方法不仅可以为数值天气预报模式提供初始场,也对多普勒激光雷达观测资料不足的地方进行弥补。满足了当前对多种气象参数的要求,而且随着计算机技术的发展使得短时间计算大量数据成为可能,该技术应该是最有前途的方法。

结合上述在微波天气雷达的反演算法在多普勒激光雷达中的改进及创新算法可以大体归结为以下内容(具体见表1)。

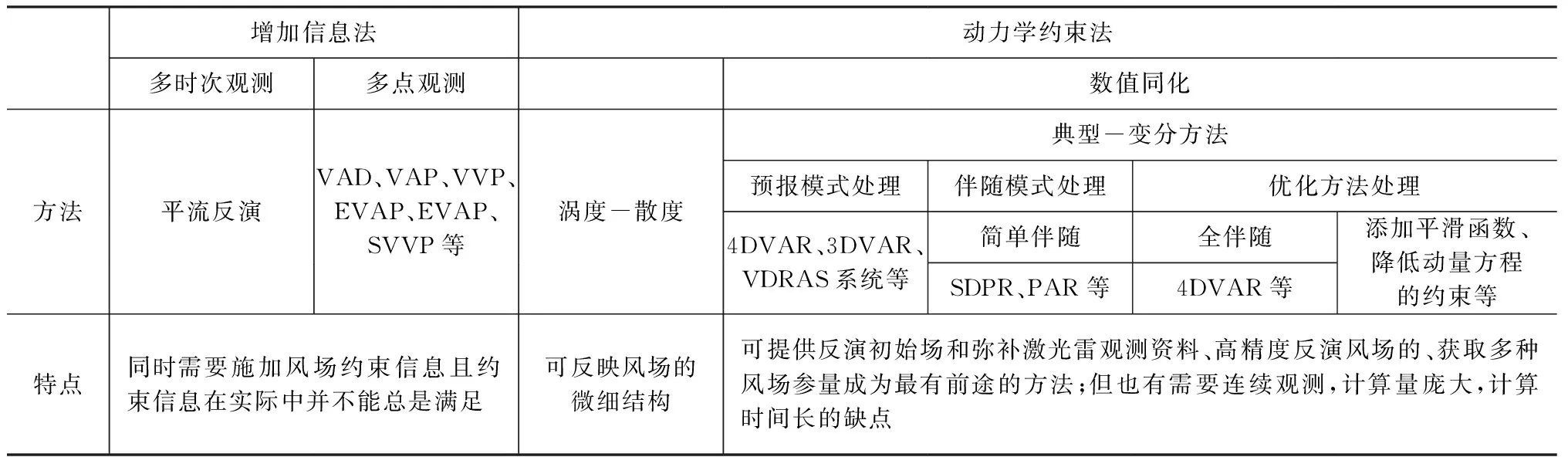
表1 单部多普勒激光雷达主要反演算法的分类

3 多部(两部及以上)多普勒激光雷达风场反演研究

早期的研究重点解决观测点的同一性问题。1969年,Armijo[21]首次在笛卡尔坐标系中构建多部普勒雷达探测大气风场的方程组,多部多普勒雷达的风场反演有了一定的发展。Lhermitte和Miller[22]最先提出了“共面”扫描法(COPLAN),理论上双部多普勒雷达需同时获取同一目标点的信息,实际操作中不能确保这种同步性,这种方法要求雷达的体扫范围是过雷达基线的斜面确保两部多普勒雷达的原始资料尽量处于同一采样空间,减小了上述误差。之后更具体划分了两雷达之间风场反演效果较好的区域,但不易在实际操作中达到这种效果。1983年Ray等人[23]提出超定双多普勒技术(Over-Determind Dual-Doppler,ODD),利用质量连续方程的最小二乘法以及低通滤波算子对其进行补充完善,Chong等人引入了扩展ODD(Extended ODD,EODD)方法,通过欧拉方程进行反演,克服了迭代法引入的问题的同时存在一定技术上的限制,插值误差和双部雷达的不同步性等。Bousquet等基于变分的方法提出综合和连续调整技术[24](Multiple-Doppler Synthesis And Continuity Adjustment Technique,MUSCAT),不仅克服了使用迭代法和多次插值引入的误差,而且通过引入约束条件一定程度上降低了连续方程所造成的累计误差等,效果较好。

上述算法从几何角度看主要分为两种,一种为Armijo提出的笛卡尔坐标系下的反演,另一种Lhermitte等提出的圆柱坐标系下的风场反演,双部多普勒雷达下的风场反演主要基于以下几种假设:(1)忽略地球曲面的影响；(2)假设粒子下降的末速度可直接获取；(3)激光束沿直线传播；(4)两部雷达具有同步性。除假设条件下引入的误差外,笛卡尔坐标系下求解连续方程时边界的选择、对原始数据的空间插值都会增大误差。以共面法为代表的圆柱坐标系,以雷达为基准建立圆柱坐标系经过连续体扫后,在斜面上获得准确的正交分量,求解水平风速,利用连续方程获取垂直速度,需要多次插值。

从大气风场反演的理论上讲,至少需要三部多普勒雷达进行同步探测,且联合探测的最佳布局为等边三角形。在实际操作中如何保证多部多普勒雷达同时获取同一目标点的资料是早期的一个难题。三部及以上的多普勒雷达的同步观测加之合理的布局,理论上可以提高大气风场的反演精度,扩大风场的监测范围并且提高系统的稳定性。

研究发现,早期基于微波雷达的多部雷达风场反演方法,重点解决观测点的同一性问题,该问题激光多普勒雷达也依旧存在。双雷达观测覆盖区域有限,也很难发挥作用,最近十多年的研究已经不多,针对多普勒激光雷达也没有提出更有效的方法。随着变分方法的应用,单部雷达和多部雷达不再有根本的区别,同时观测点的同一性也不是问题,更多转向研究同化资料的方法反演风场。在上述单部多普勒激光雷达的研究中以变分同化为主同化方法成功的反演,为同化方法在多部多普勒激光雷达上的使用提供了依据。

4 总结与展望

本文在微波雷达风场反演发展的基础上介绍不同个数下的多普勒激光雷达的风场反演方法,根据多普勒雷达个数的不同可分为单部多普勒激光雷达和多部多普勒激光雷达风场反演。

20世纪70年代到20世纪末,由于多普勒天气雷达在发达国家的布设引发了风场反演的研究热情,提出了许多不同的方法。随着多普勒激光雷达的发展将微波雷达的风场算法进一步应用和创新,重点偏向于单部多普勒激光雷达的研究。研究发现,单部多普勒激光雷达由于观测信息先天不足以及观测误差的影响,第一类方法中大多基于均匀或线性风场的假设下利用径向风速反演,很多情况下反演方法精度不高,在实际的风场在业务预报中几乎没有发挥作用。双雷达观测覆盖区域有限,也很难发挥作用。因此最近十多年相关研究已经不多,也没有提出更有效的方法,且在多普勒激光雷达上也没有太大的创新,而更多的研究转向多普勒激光雷达资料的同化,且变分方法应用后单部多普勒激光雷达和多部多普勒激光雷达就不再有根本的区别,多部激光雷达的同一性也不是问题。变分方法不仅可以得到高精度的风场反演结果,还能获取其他气象参量,变分同化方法应该是最有前景的方法。同化方法利用完整的大气模式和模拟结构作为约束条件获取的风场可信度更高。随着计算机技术的发展和同化技术在激光多普勒雷达中的改进,进而在业务中实现应用。