隐性轨迹题型面面观

■福建省龙岩市永定区城关中学 (特级教师)

我们在解题时常碰到隐性轨迹问题，隐性轨迹就是轨迹不太明显，需要我们去发现。理论上说，我们学过的轨迹都可能成为隐性轨迹，下面我们就谈谈常见的隐性轨迹问题。

1.隐性轨迹是直线或在直线上的某些点

例1已知圆C1：x2+y2=4与圆C2：(x-3)2+(y-3)2=4，过动点P(a，b)分别作圆C1，圆C2的切线PM，PN(M，N分别为切点)，若|PM|=|PN|，则a2+b2-4a-6b+13的最小值是( )。

解析：由题意知PM⊥C1M，PN⊥C2N，C1(0，0)，C2(3，3)。

由|PM|=|PN|，得|PC1|2-4=|PC2|2-4，即a2+b2=(a-3)2+(b-3)2，则a+b=3。

a2+b2-4a-6b+13=(a-2)2+(b-3)2。

图1

至此，我们有两种解决问题的方法。

法一：这式子可看成是定点(2，3)到直线x+y=3 上动点(a，b)的距离的平方，在直线外定点到直线上动点的距离中，垂直线段最短。

故(a-2)2+(b-3)2的最小值为最短距离的平方，即=2。选B。

法二：(a-2)2+(b-3)2=(a-2)2+a2=2a2-4a+4=2(a-1)2+2≥2，当且仅当a=1时取得最小值2，选B。

点评：法一通过隐性轨迹转化为点到直线的距离问题，法二通过配方法求得最小值。

例2设Sn为等差数列{an}的前n项和，若(m≠n)，则Sm+n-4的符号是( )。

A.正 B.负

C.非负 D.非正

2.隐性轨迹是圆或圆弧

例3(2020年北京卷第5题)如图2，已知半径为1的圆经过点(3，4)，则其圆心到原点距离的最小值为( )。

A.4 B.5

C.6 D.7

图2

解析：设圆心为C(x，y)，则，化简得(x-3)2+(y-4)2=1。

由图知，|OC|+1≥|OM|=5，即|OC|≥5-1=4，当且仅当C在线段OM上时取得等号，选A。

点评：圆心C的轨迹是以M(3，4)为圆心，1 为半径的圆，所以|OC|的最大值是|OM|+1，最小值是|OM|-1。

例4(龙岩市2020 年5 月质检题理数第11 题)如图3，在棱长为2 的正方体ABCD-A1B1C1D1中，P是正方形ADD1A1内(包括边界)的动点，M是CD的中点，且∠PBA=∠PMD，则当△PAD的面积最大时，|PA|的值为( )。

解析：由题意可知，|PA|=2|PD|，以AD所在直 线 为x轴，AD的 中垂线为y轴建立直角坐标系，设A(-1，0)，D(1，0)。设P(x，y)，所以(x+1)2+y2=4(x-1)2+4y2。

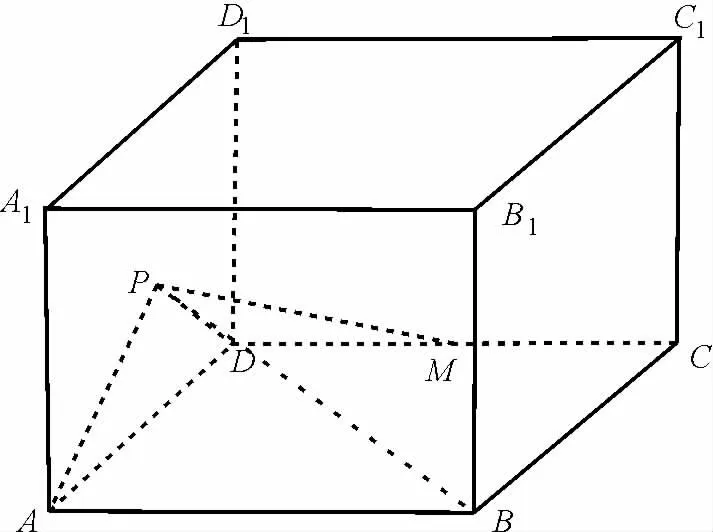
图3

点评：本题是立体几何与解析几何的综合问题，难点之一是要探求点P在平面ADD1A1满足的条件，难点之二是在此条件下求出点P的轨迹(阿波罗尼斯圆弧)。

例5(龙岩市2020 年高中毕业班3月月考卷)已知数列{an}满足an+1=2+，则a1+a2020的最大值是( )。

3.隐性轨迹是椭圆

根据椭圆性质，可得|PE|的最大值为3。

点评：说是通过定义解答了本题，其实是从许多的隐性轨迹转化而成的，一是点A在以E为圆心，4 为半径的圆上，即得到|AE|=4;二是PQ为线段AF的中垂线;三是点P在AE上，然后落实在|PE|+|PF|=4这个定值上，点P在右端点时取到最大值。

4.隐性轨迹是抛物线

图4

例7如图4，三条直线a、b、c两两平行，直线a、b间的距离为p，直线b、c间的距离为，A、B为直线a上两定点，且|AB|=2p，MN是在直线b上滑动的长度为2p的线段。假设d是△AMN的外心C到直线c的距离，试探求：当△AMN的外心C在什么位置时，d+|BC|最小，最小值是多少?

解析：以直线b为x轴，以过A点且与直线b垂直的直线为y轴建立直角坐标系。

设△AMN的 外 心 为C(x，y)，则A(0，p)，M(x-p，0)，N(x+p，0)。

由题意知|CA|=|CM|，故：

化简得x2=2py。

点C的轨迹是以原点为顶点，y轴为对称轴，开口向上的抛物线E。

由此可得直线c恰为轨迹E的准线。

由抛物线的定义知d=|CF|，其中是抛物线的焦点。

则d+|BC|=|CF|+|BC|。

线段BF与抛物线的交点即为所求的点。

点评：求出点C的轨迹是解决问题的关键。本题似曾相识，却又很新颖，有较强的探究性。