直击圆锥曲线最值问题的解题策略

■江苏省太仓市明德高级中学

圆锥曲线的最值(范围)问题，因考查知识容较多、分析能力要求高、区分度高而成为高考命题的一个热点。由于这类问题解法灵活且综合性较强，故而成为高考的一大难点。那么，突破这一难点有哪些基本策略呢? 下面举例说明。

一、利用圆锥曲线定义

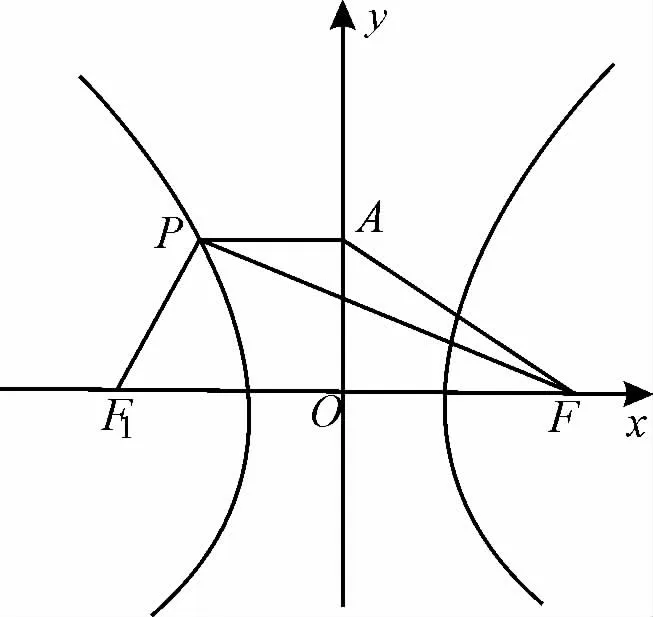
图1

例1如图1，已知点P在离心率为2 的双曲线=1的左支上，A(0，)，F是 双 曲 线 的 右 焦点，若△PAF周长的最小值是20，则此时△PAF的面积为( )。

解析：先由双曲线的定义可知△PAF周长的最小值等于|AF1|+|AF|+2a，再根据离心率的值可求出双曲线方程，然后直线AF1与双曲线联立即可求出P点的坐标，最后利用S△PAF=S△AF1F-S△PF1F求出面积。

设双曲线的左焦点为F1，由题可知，|PF|-|PF1|=2a，|PF|=2a+|PF1|。

图2

如图2，△PAF的周长=|AP|+|PF|+|AF|=|AP|+|PF1|+|AF|+2a≥|AF1|+|AF|+2a，当且仅当A，P，F1三点共线时取等号。

因此，|AF1|+|AF|+2a=20。

点评：对于某些椭圆或双曲线中的最值问题，通常利用定义把到左焦点的距离转化为到右焦点的距离，反之亦然;对于抛物线中的最值问题，同样可依据定义把到焦点的距离转化为到准线的距离，反之亦然。这些方法的本质是利用几何关系求最值。

二、利用基本不等式

例2(1)抛物线y2=2px(p＞0)的焦点为F，已知点A，B为抛物线上的两个动点，且满足∠AFB=120°。过弦AB的中点M作抛物线准线的垂线MN，垂足为N，则的最大值为( )。

(2)设抛物线y2=2x的焦点为F，过F的直线交该抛物线于A、B，则|AF|+4|BF|的最小值为_____。

点评：当依据题意得到关于求最值的表达式含有两个未知数时，一般利用基本不等式求最值，但必须先要判断是否满足“一正二定三相等”。

三、转化为函数的最值问题

图3

例3在等腰梯形ABCD中，AB∥CD，且|AB|=2，|AD|=1，|CD|=2x，其 中x∈(0，1)。以A，B为焦点且过点D的双曲线的离心率为e1，以C，D为焦点且过点A的椭圆的离心率为e2，若对任意x∈(0，1)，不等式t＜e1+e2恒成立，则t的最大值为( )。

解析：在等腰梯形ABCD中，由余弦定理得：

点评：依据题意建立目标函数时，一定要注意自变量的取值范围，同时注意在求函数的最值时，遇到复杂函数采用换元法可以化繁为简，还要关注函数的单调性。

巩固练习

1.已知点R(0，2)，曲线C：y4=(px)2(p＞0)，直线y=m(m＞0且m≠2)与曲线C交于M，N两点，若△RMN周长的最小值为2，则p的值为( )。

A.8 B.6

C.4 D.2

2.已知F1，F2是椭圆和双曲线的公共焦点，P是它们的一个公共点，且∠F1PF2=，则椭圆和双曲线的离心率乘积的最小值为_____。