用圆锥曲线的定义解题

■甘肃省白银市第一中学

圆锥曲线是高中数学学习的重要内容，同时也是高考考查的重点内容，而圆锥曲线的定义不仅是推导圆锥曲线方程及性质的基础，而且也是解题的重要工具。

一、椭圆问题

二、双曲线问题

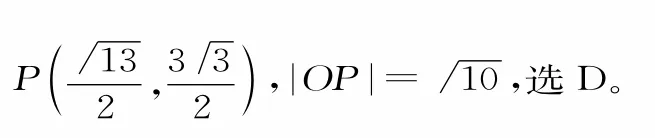
三、抛物线问题

例5若点P到直线x=-1的距离比它到点(2，0)的距离小1，则点P的轨迹为( )。

A.圆 B.椭圆

C.双曲线 D.抛物线

解析：点P(x，y)到直线x=-1的距离比它到点F(2，0)的距离小1，则点P(x，y)到直线x=-2的距离与它到点F(2，0)的距离相等，所以动点P的轨迹是以F(2，0)为焦点的抛物线，得=2，即p=4。于是P的轨迹方程为y2=8x，选D。

练习已知是动点M满足的坐标方程，则M的轨迹方程为( )。

A.圆 B.椭圆

C.双曲线 D.抛物线

解析：因为动点M满足的坐标方程，此方程表示的是动点M(x，y)到定点(0，0)与定直线3x+4y-12的距离相等，且定点不在定直线上，根据抛物线的定义知动点的轨迹是以定点为焦点，定直线为准线的抛物线。选D。

例6在抛物线y2=2x上求一点P，使P到焦点F与到点A(3，2)的距离之和最小。

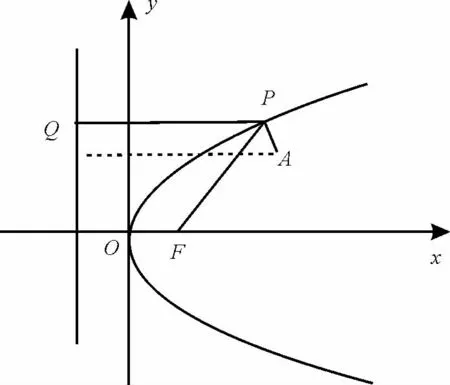
图1

解析：如图1，设抛物线上的点P到准线的距离为|PQ|。

由抛物线定义可知：

|PF|+|PA|=|PQ|+|PA|＞|QA|。显然当P、Q、A三点共线时，|PQ|+|PA|最小。

因为A(3，2)，将y=2代入y2=2x，得x=2，所以P点坐标为(2，2)。