无油线性压缩机的频率特性和活塞偏移特性研究

2021-02-06李诚展李建国蔡京辉

振动与冲击 2021年3期

李诚展, 李建国, 孙建, 蔡京辉

(1.中国科学院大学,北京 100049;2.中国科学院理化技术研究所空间功热转换技术重点实验室,北京 100190)

随着技术的发展，电子电气设备在电子设备、发电厂、航天航空工业等领域被广泛应用，设备功率密度的提高使得散热量和热流密度均出现显著增长。然而由于设备本身结构的限制，传统的空冷式热沉和翅片结构不能有效地满足排热需求，因此需要寻求更加高效的冷却方式。微型蒸汽压缩式制冷循环以其显著的效率和优良的性能在电子冷却中有明显的优势[1]。Liang等[2]指出线性压缩机相比其他类型压缩机在电子冷却应用中有很多优势。线性压缩机摒弃了传统活塞压缩机中的传动机构[3]，采用线性电机直接驱动活塞运动，同时采用径轴向刚度较大的板弹簧作为径向支撑，活塞受到的径向力极小，保证活塞与气缸的间隙密封，减少了活塞受到的摩擦损失，压缩机机械效率得以提升，比传统的活塞压缩机总体效率高20%[4]。线性压缩机采用自由活塞结构，可通过改变活塞行程来对容量进行实时调节以适应外界热负荷的变化。但间隙密封技术的应用使得压缩腔内气体通过间隙向背压腔的泄漏，在一个周期内，压缩腔和背压腔之间时均泄漏量不为零，压缩腔平均压力和背压腔的压力存在压差，加之线性压缩机采用自由活塞结构使得活塞运动中心出现偏移[5]。这是线性压缩机的显著特点之一。活塞运动中心的偏移会使得在同样行程下压缩机容积效率下降；同时活塞运动中心的偏移量随着工况变化而变化，对压缩机的控制带来了很大的挑战，因此，明确活塞中心位置偏移量对提高压缩机性能和压缩机控制来说都是十分必要的。线性压缩机是一种典型的质块-阻尼器-弹簧组成的机械振动系统，其另一个显著特点是在共振频率下运行时，直线电机的效率最高[6]。众所周知，振动系统的共振频率与弹簧刚度和质块的质量有关。振动系统的弹簧刚度主要包括两部分，一部分是机械弹簧刚度，另一部分就是气缸内气体力对系统产生的类似弹簧作用的气体等效弹簧刚度[7]。气体等效弹簧刚度随着工况而发生变化，共振频率也会随之变化，因此很有必要对气体等效弹簧刚度值进行有效的预测，以便在压缩机运行时能根据工况来实时调整运行频率。目前用来计算气体等效弹簧刚度的模型有两种，一种简化的线性等效模型，也被称作平均值法[8-10]；另一种是傅里叶变换的方法[11]。因此需要对这两种方法的计算结果进行比较，以便于对压缩机的共振频率准确的预测。

针对线性压缩机随着工况和热负荷变化而引起共振频率和活塞偏移发生变化问题，本文建立了关于压缩机共振频率的线性等效模型和傅里叶变换计算模型，分析了活塞行程、排气压力对共振频率的影响，并与实验结果进行了对比。同时利用傅里叶变换计算模型对活塞的偏移量进行了预测，分析了活塞行程、排气压力和运行频率对活塞偏移量的影响，并通过实验对计算结果进行验证。

1 线性压缩机结构及原理

线性压缩机样机为动圈式线性压缩机，具有动质量小、径向力小和启动转矩低等优点。图1为动圈式线性压缩机结构示意图，主要包括动圈式线性电机部分、支撑结构部分和气体压缩结构部分。动圈式直线电机部分由线圈、永磁体、回铁组成，支撑结构部分采用的是径轴向刚度比较大的板弹簧，气体压缩结构部分主要包括活塞、气缸和吸排气阀组。活塞与线圈通过连接件组成一个动部件，被称为动子，由动圈式直线电机直接驱动。板弹簧作为谐振弹簧，同时保证了活塞与气缸之间的间隙密封，进而实现了压缩机的无油润滑。为进一步提高压缩机的运行效率，降低流动阻力和吸气再热损失，将压缩机的吸气阀安装在具有环形气流通道的活塞前端面，排气阀安装在气缸顶端，形成轴向流动的吸排气流道。当向压缩机的线圈中通以交流电，线圈在与永磁体产生的磁场的相互作用下进行往复运动，从而带动活塞运动。当活塞在上止点时，排气阀关闭，开始反向运动，余隙容积中残留的高压气体就会膨胀，直至气缸内部压力低于吸气腔或者吸气流道的压力时，吸气阀打开，开始吸气过程，随后活塞运动到下止点时，吸气过程结束，吸气阀关闭，活塞再次进行反向运动，开始逐步压缩气缸内的气体，当气缸内气体压力高于排气腔的压力时，排气阀打开，排气过程开始，直至运动到上止点，此过程结束，气缸内气体重新开始膨胀过程，如此形成周期性的排气、膨胀、吸气和压缩四个工作阶段。

图1 压缩机结构示意图

2 数学模型

2.1 简单线性等效模型

Cadman等[12]提出了一种简单线性化计算模型，也称作平均值法，即在压力-活塞位移图中，压缩过程和膨胀过程起点之间的斜率即为等效气体弹簧刚度值，如图2所示。因此等效的气体弹簧刚度kg为

图2 压缩机的压力-活塞位移图

(1)

式中：psuc和pdis分别为压缩机的名义吸、排气压力，Ap为活塞面积，xs为活塞行程。

从而压缩机振动系统的等效总刚度k为

k=kg+ks

(2)

式中,ks为板弹簧的弹簧刚度。

共振频率为

(3)

式中:mmov为振动系统的等效动质量，包括活塞、线圈、板弹簧质量的三分之一以及连接件的质量[13]。

2.2 傅里叶变换计算模型

通过对机械系统进行受力分析，根据牛顿第二定律可得系统的振动方程为

(4)

式中:mmov为动子质量；x(t)为实时活塞位移；ks为板弹簧弹簧刚度；cm为系统机械阻尼系数；Fg(t)为气体；k0为电机常数，i(t)为实时电流，其表达式为

Fg(t)=Ap(pcyl(t)-pb)

(5)

式中:pcyl(t)为气缸气体压力；pb为背压腔气体压力，这里背压腔压力等于吸气压力。

压缩腔的工作过程分为吸气、压缩、排气和膨胀四个阶段，为了简化气体力计算，针对气体力提出以下假设：

(1)将吸排气阀当作理想阀来处理，即认为吸排气过程中不存在压力波动；

(2)压缩和膨胀过程当做多变指数为n的多变过程；

(3)压缩、排气和膨胀阶段不存在泄漏。

基于上述假定，其p-V示功图可如图4～7所示，图中V0=x0Ap，Vs=xsAp。

因此气缸中吸气、压缩、排气和膨胀四个过程的气体力可表示为

(6)

式中：x0为压缩机未运行时活塞的位置。

对于直线压缩机来说，忽略电磁推力系数、等效电阻和等效电感等参数的非线性特性影响，仅气体力存在非线性特性，会产生高次的谐波分量，但由于机械振动系统的低通滤波特性，并且一般来说机械弹簧力会高于气体力，因此，在正弦电压驱动下，在稳态下活塞的振动曲线很接近谐波曲线，因此，振动系统的动力学方程可以通过描述函数法来求解，同时气体力表示为等效弹簧力、等效阻尼力和等效的静态力之和：

(7)

式中:kg为气体等效弹簧刚度，cg气体等效阻尼系数，Fs为等效的静态力。

此时系统的振动方程可表示为

(8)

由于气体力是周期性函数，从数学上可知，该周期函数可以展开为Fourier级数，即无数个谐波函数与常数项的和：

(9)

其中，

(10)

(11)

(12)

对于式(9)中常数项即气体力在一个周期内的平均值，称为直流分量。

根据相关的研究[13]表明，气体力的高次谐波分量对其幅值影响作用较小，且由于直线电机具有带通滤波特性，因此对于处于一定基频ω(ω=2π/T)激励的振动而言，取一阶谐波分量与直流分量即可，因此气体力可等效为：

Fg=a1cosωt+b1sinωt+Fs

(13)

(14)

(15)

(16)

将气体力的表达式(5)和(6)以及代入上式可得气体力的傅里叶级数展开式中的谐波的幅值和直流分量的表达式，同时对照式(7)和(13)可以得出气体等效参数。

气体等效弹簧刚度kg为

(17)

气体等效阻尼系数cg为

(18)

由于压缩机运行时，压缩腔与背压腔存在压力差，因此会产生一个轴向的静态力，就会压缩机械弹簧，从而引起活塞中心位置发生偏移，而Fs表示气体力在一个周期内的平均值，根据振动理论[14]可知，该平均值相当于恒力，作用于振动系统上，使系统产生一个静变形，即活塞中心位置产生偏移，因此活塞中心位置的偏移量可表示为：

(19)

3 实验装置

图3即为测量压缩机共振频率和活塞偏移量而搭建的实验平台的系统示意图。主要包括蒸发器，线性压缩机，冷凝器，质量流量计，干燥过滤器和膨胀阀。蒸发器处的冷量采用电加热的形式来进行测试。西门子的质量流量计(SITRANS FC MASSFLO MASS2100，精度为±0.5%)用来测量液体制冷剂的质量流量。6个Pt100铂电阻温度计(精度为±0.1 K)分别安装在蒸发器的进出口，压缩机的进出口，冷凝器出口，膨胀阀入口。两个压力传感器(精度为±0.5%)用来测量压缩机的吸排气压力。压缩机的驱动电源采用的是NF EC1000S型号的交直流电源，用以实现对压缩机工作电压和运行频率的调节。两台功率计(PF9811，精度为±0.4%)分别用来测量压缩机的输入功率和对蒸发器的加热功率。为了便于测量活塞位移，压缩机后壳采用带有石英玻璃的可视化窗口，通过激光位移传感器(Keyence，LK-H080，分辨率为1 μm)进行测量。通过示波器可以显示出位移运动曲线，通过示波器可以显示出活塞运动中心的偏移量，为了降低实验过程中压缩机振动对位移测量的影响，将压缩机与激光位移传感器通过工装固定在石英台上。实验中所用采集板卡为Keithley 7700，用以采集实验中温度传感器和压力传感器的数值，通过软件Labview以Excel表格的形式存储至计算机中。

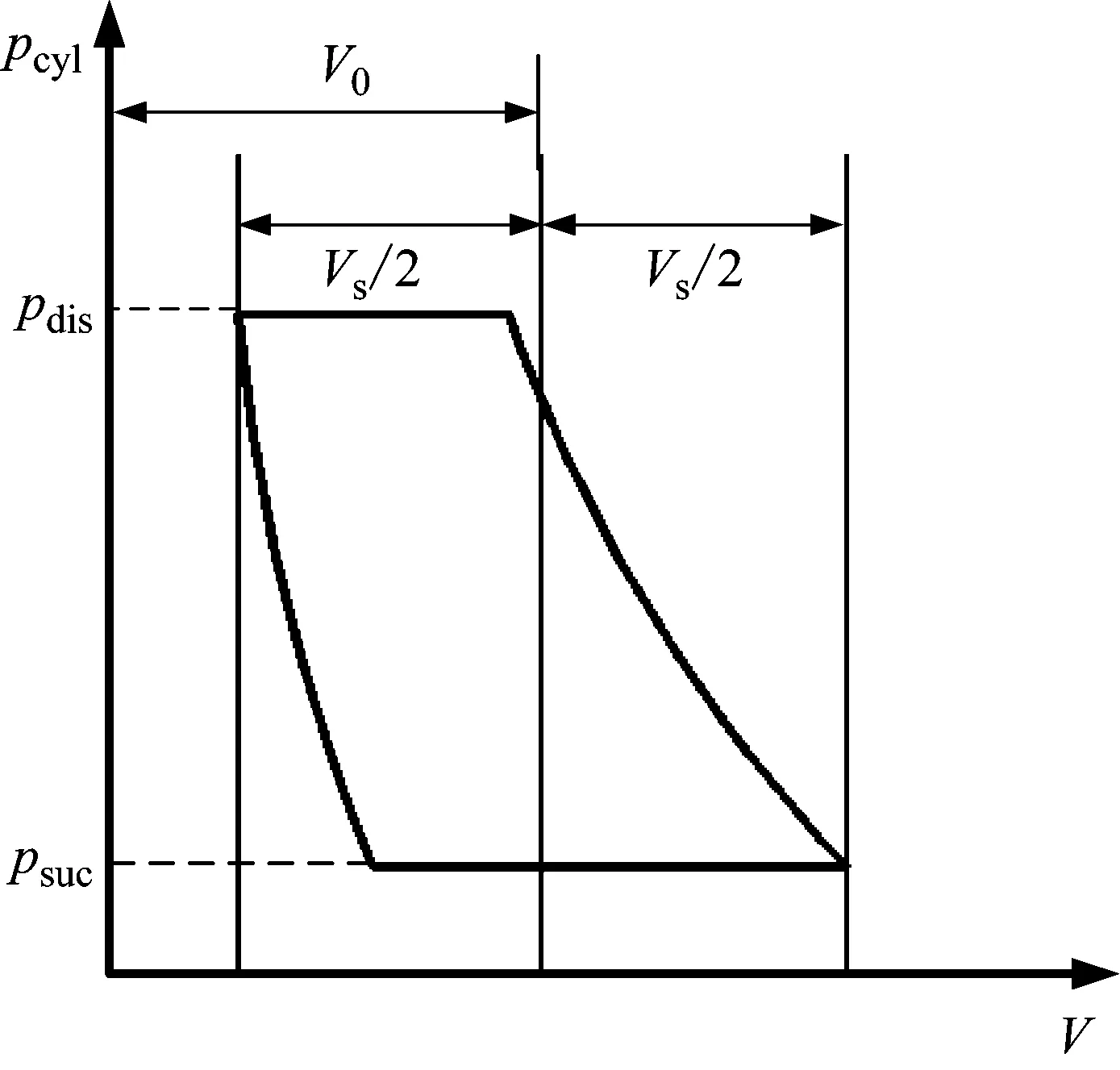
图3 压缩机简化示功图

图4 压缩机测试系统图

实验中向制冷系统中充注一定量的制冷工质R134a，在不同参数下(行程、排气压力、频率)对线性压缩机进行测试，并记录下压缩机的输入功率和蒸发器的电加热量，实验室周围环境温度设定为25 ℃。实验中，活塞的行程的改变是通过调节驱动电源的输入电压来实现。从实验中可以计算得出系统的制冷量和COP，容积效率和等熵效率。计算公式如下：

(20)

(21)

式中,Pin为压缩机的输入功率。

压缩机容积效率为

(22)

式中:ρsuc为压缩机入口气体密度，f为压缩机驱动频率。

压缩机的等熵效率为

(23)

式中:hdis,ise为排气压力下等熵条件得出的制冷剂的比焓值；hsuc为吸气状态下制冷剂的比焓值。

根据误差传递函数计算可以得到各个导出参数的误差，表1给出了该实验中主要的导出参数的测量范围及其误差。

表1 各个参数的误差范围

4 结果与分析

4.1 共振频率的测量

本节是通过实验测量系统的电机效率从而确定压缩机的共振频率来验证这两种模型的准确性。因此首先介绍一下共振频率的测量和实验结果。实验时，通过逐渐改变驱动电源的运行频率，并改变输入电压来保持其行程恒定，并通过调节节流阀来保证压缩机的吸排气压力相同，当实验中铜损最小时，即电流最小时，此时对应的电机效率最高，此时对应的频率即为共振频率。电机效率的计算式为

(24)

式中:R为压缩机线圈电阻，Irms为电流的有效值。

图5给出了在行程为8.5 mm，吸排气压力分别为0.35 MPa和0.887 MPa时，不同频率下的电机效率，从图中可以看出在频率为62.5 Hz时，此时电机效率最大，即为共振频率。

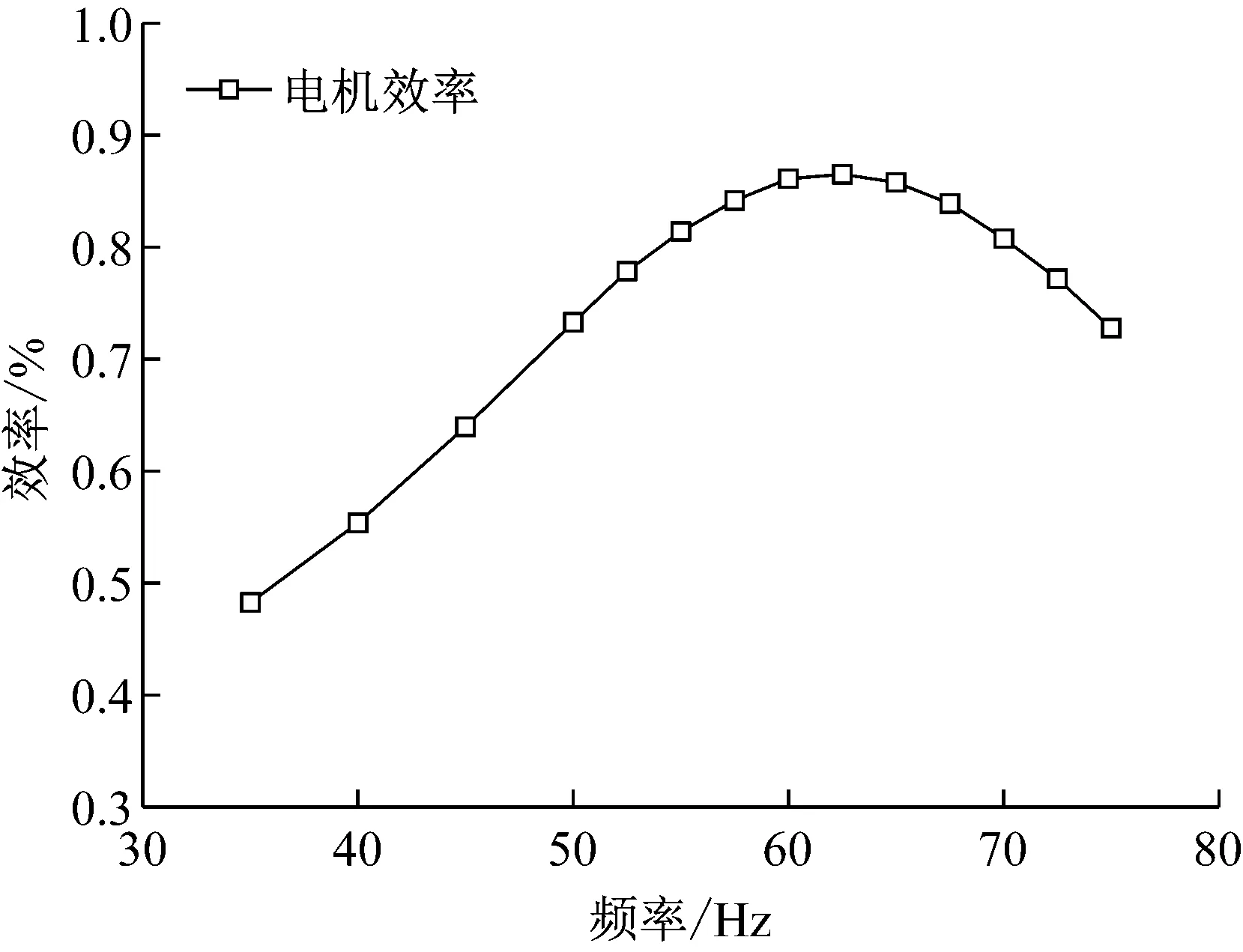
图5 不同频率下的电机效率

4.2 活塞行程对压缩机频率特性的影响

图6给出了不同行程下压缩机共振频率的测量值与两种模型的计算值。实验和计算时，保持压缩机吸排气压力相等(吸气压力和排气压力分别为0.35 MPa和0.887 MPa)。从图中可以看出，压缩机的共振频率随着行程的增加逐渐减少，实验测量值和两种模型计算值的变化趋势是相同的。但实验测量值高于两种模型的计算值，在活塞行程较低时，傅里叶变换计算模型计算值更接近测量值，而在活塞较高时，简单线性化模型计算值则更接近实验值，总体来看，简单线性化模型更接近实验测量值。傅里叶变换计算模型在行程6.5 mm时，所得计算值与实验值的误差最小，为4.5%；而此模型在行程为9.5 mm时，误差最大，为9.5%。简单线性化模型在行程6.5～9.5 mm的计算值，误差范围为4.8%～7.1%，这表明二者的计算值与实验值的误差都在10%之内。从图中可以看出，计算值是低于实验值，这可以通过计算中所采用的等效气体弹簧刚度是低于实际实验中的等效气体弹簧刚度值。等效气体弹簧从物理意义上来讲，是由于压缩机气缸前端存在余隙容积所引起的，在压缩机运行时，由于余隙容积的存在，在压缩腔内部始终残存着高压气体，在膨胀阶段可以回收利用余隙容积中残存气体所储存的能量，这就类似储能元件弹簧的作用，因此可以将此部分等效为气体弹簧[14]，此部分弹簧等效的弹簧刚度系数为kg。在计算时由于只考虑了余隙长度对应的余隙容积里面的残存气体，但实际上由于压缩机中气缸前端阀板处存在排气孔，同时可能由于排气阀片关闭不严引起排气腔内高压气体向压缩腔内的气体进行泄漏，这些因素都使得压缩腔内残存的高压气体量会高于计算值，使得等效气体弹簧刚度值高于计算值。因此，共振频率的实测值会高于计算值。

图6 不同行程下的共振频率的计算值与实验值对比

4.3 排气压力对压缩机频率特性的影响

固定压缩机行程(8.5 mm)和吸气压力(0.35 MPa)，测量和计算压缩机的共振频率。图7给出了不同排气压力下压缩机的共振频率的测量值和两种模型的计算值。从图中可以看出，随着排气压力的增加，压缩机的共振频率逐渐增大，实验测量值和两种模型计算值的变化趋势是相同的。但实验测量值高于两种模型的计算值，简单线性化模型更接近实验测量值。但两者的计算值与实验值的误差都在10%之内。描述函数法模型在吸排气压差为0.67 MPa时，所得计算值与实验值的误差最小，为7.0%；而此模型在压差为0.42 MPa时，误差最大，为9.5%。简单线性化模型在压差0.42～0.67 MPa的计算值，误差范围为5.9%～7.7%，计算值与实验值的误差都在10%之内。

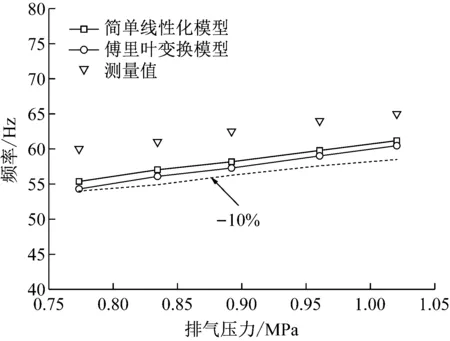
图7 不同排气压力下的共振频率的计算值与实验值对比

4.4 压缩机振动系统的非共振特性

为了进一步确认模型的适用性，对压缩机的在偏移共振频率-12%～8%的制冷性能进行了研究。图8给出了55～67.5 Hz范围内压缩机的COP、电机效率、容积效率和等熵效率。从图中可以看出，COP和电机效率随着频率的增加先增加后逐渐减小；容积效率和等熵效率随着频率增加接近一致，上下变化范围在6%之内。共振频率为62.5 Hz，在两端即55 Hz和67.5 Hz时，压缩机的COP分别比共振频率下相比降低了5.9%和3.7%，而电机效率分别降低了5.9%和2.9%。在偏移共振频率-12%～8%的运行频率范围内，其制冷性能降低范围是可以接受的，因此，在压缩机实际运行控制中，在压差在0.42～0.67 MPa的范围内，可以采用两种模型的计算值来进行运行控制，其中采用简单线性化模型的计算值更接近实验测量值，推荐采用简单线性化模型。

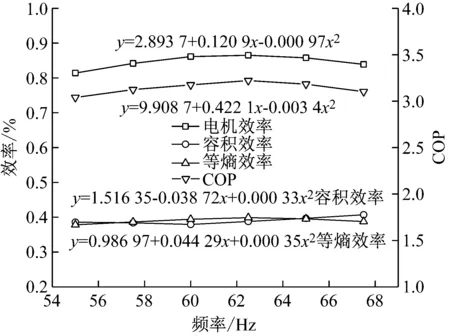
图8 非共振特性下压缩机的效率和COP

4.5 活塞行程对活塞运动中心位置偏移量的影响

实验测量装置采用图4所示，实验中通过调节输入电压来调节压缩机行程，并通过调节节流阀开度来保持吸气压力和排气压力一致。通过激光位移传感器记录下活塞的行程，并通过示波器显示出活塞在不同行程下偏移量的大小。图9给出了两种不同工况下不同行程下活塞的偏移量的计算值和实验测量值。从图中可以看出，实验测得的活塞中心位置的偏移量随着行程的增加总体呈减小趋势，但减小并不大，在8%之内，可认为活塞偏移量随行程不变。通过式(19)计算得出的中心位置的偏移量随着行程的增加逐渐减小，但随着行程的增加，计算的偏移量逐渐接近实验测量值，并在接近活塞的上止点的位置，通过计算的偏移量与实验测量值相差较小，不高于10%。实验测量值低于计算值是因为在计算假设中并未考虑通过活塞与气缸之间的间隙泄漏所引起的。

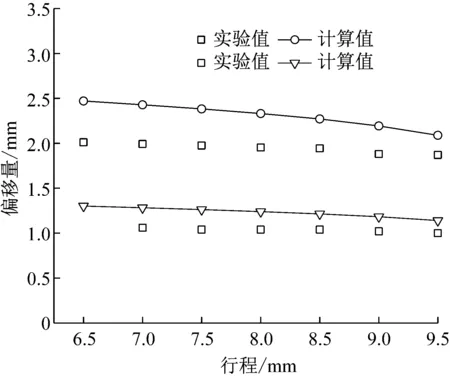
图9 不同行程下活塞中心位置的偏移量

因此，根据对不同行程下活塞中心位置偏移的实测结果，可以得出活塞中心位置的偏移随着行程变化可以忽略，且可以通过式(19)计算在行程等于上止点的活塞中心位置偏移量来得到。

4.6 排气压力对活塞运动中心位置偏移量的影响

在探究排气压力对活塞中心位置偏移量的影响时，固定活塞行程为8.5 mm，保持吸气压力不变，通过调节输入电压和节流阀开度使得排气压力逐渐增大。图10给出了不同排气压力下活塞中心位置的偏移量的计算值和实验测量值。从图中可以看出，随着排气压力的增大，活塞中心位置偏移量的测量值逐渐增大，从1.68 mm逐渐增大至2.35 mm。图10中的计算值是采用式(19)在行程等于上止点时所计算得出的中心位置的偏移量，与实验测量值相差很小，不超过10%，这进一步验证了此种计算方法的正确性。

图10 不同排气压力下活塞中心位置的偏移量

4.7 运行频率对活塞运动中心位置偏移量的影响

由于压缩腔向背压腔的泄漏是在一个周期内产生的结果，因此有必要考察一下运行频率对偏移量的影响。固定压缩机行程为8.5 mm，通过调节膨胀阀和输入电压使其吸排气压力保持一致，逐步增加压缩机的运行频率。图11给出了不同频率下活塞中心位置的偏移量。从图中可以看出，随着运行频率的增加(50 Hz增加至75 Hz)，活塞的中心位置的偏移量逐渐增加，这表明一个周期内的通过间隙的泄漏量逐渐增加。频率从50 Hz增加至75 Hz，偏移量从1.9 mm增加至2.2 mm，增长了15%。但采用式(19)所得结果是活塞的偏移量不随频率而发生变化，这与实验结果不符。实际上，线性压缩机在共振频率中运行，工况和热负荷变化会引起共振频率的变化，但共振频率的波动范围较低，因此偏移量随频率的变化并不大，因此，在实际控制中可以忽略频率对活塞中心位置偏移的影响。