α稳定分布噪声下非对称三稳系统的随机共振特性分析

张 刚，谢 攀，张天骐

(重庆邮电大学 通信与信息工程学院，重庆 400065)

随着非线性动力学和统计物理理论的不断发展，随机共振(Stochastic Resonance, SR)[1-5]方法的提出为信号处理领域开辟了新的思路和方法。有别于传统抑制噪声的信号检测方法，随机共振是利用噪声、信号和非线性系统之间的协同作用，将噪声部分能量转移到信号上，实现检测微弱信号的目的[6-10]。调节系统结构参数[11-12]和噪声的强度，均可诱导实现随机共振。

近年来，学者们研究的系统势函数主要是对称的，而对于非对称系统的随机共振关注较少，但是在实际工程应用中，系统对称性是不能保证的，故磁通量闸门磁力计量器与超导量子干涉设备中利用势阱非对称性来检测微弱信号[13-14]。与对称系统相比，非对称系统具有更普适的理论基础和实用价值[15]。Zhang等[16]探究了乘性与加性高斯白噪声环境中非对称双稳系统随机共振以及在轴承故障检测中的运用，张晓燕等[17]通过解析方法探究了白噪声和周期矩形信号对时滞非对称单稳系统共振的影响。

目前对高斯噪声环境中随机共振[18-19]的研究已相对成熟，然而在实际工程应用中遇到的噪声大多数都是非高斯分布的，它们具有明显脉冲特性与拖尾特性[20]，所以需要α稳定分布噪声[21-22]来模拟这些特征。α稳定分布噪声满足广义中心极限定理分布，高斯分布是其中一种特殊情况，所以研究α稳定分布噪声环境下的随机共振现象比高斯噪声环境更具有现实价值。焦尚彬等[23-24]探究了α稳定分布噪声环境中时滞非对称单稳系统和非对称双稳系统的随机共振以及参数诱导和噪声诱导对信噪比增益的影响。

通过对已有非对称系统研究成果分析，基本上研究的都是非对称单稳系统或非对称双稳系统，关于α稳定分布噪声环境中非对称三稳系统随机共振尚未见诸报道。因此，本文将α稳定分布噪声与非对称三稳系统相结合，以A-SNRI为衡量指标，首先对非对称三稳势函数进行了分析，然后探究了非对称三稳系统检测微弱信号的能力，最后分析了α稳定分布噪声不同特征指数α(0<α≤2)，对称参数β(-1≤β≤1)时结构参数a、b、偏度r和强度放大系数D对系统共振作用规律，为自适应算法实现随机共振中合理选择参数范围提供了参考依据。

1 随机共振模型

非对称三稳系统模型可以用Langevin方程(LE)[25]描述为：

(1)

式中:U(x)是非对称三稳势函数，A是微弱周期信号幅值，f是信号特征频率，ξ(t)为α稳定分布噪声，D代表ξ(t)的放大系数，通过调节D可以改变ξ(t)的强度。

经典对称三稳系统势函数形状如图1所示，表达式如下[26]：

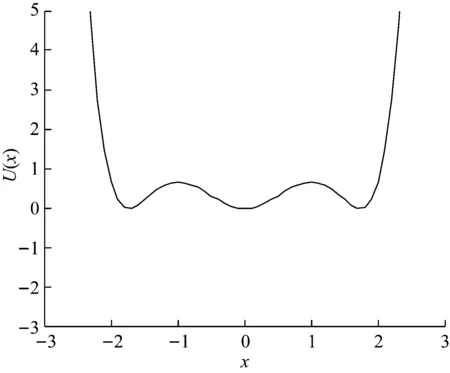
图1 经典对称三稳势函数

(2)

本文提出的非对称三稳势函数，在式(2)的基础上引入了偏度系数r,刻画了系统的非对称性。其势函数表达式为：

(3)

式中:参数a>0,b>0,c>0,r≠0，为了简化分析，在后面的研究中c都取为1。当r为0时，此时U(x)退化为经典对称三稳势函数。

图2表示刻画系统偏度r对势函数形状的影响。由图2可观察到，势函数形状是非对称的。当r>0时，势函数向右偏，当r<0时，势函数向左偏，当r的绝对值相等时，势函数向左或向右偏的幅度是相同的。由此可以推测，当r的绝对值相等时对系统的影响是一样的。

图2 非对称三稳势函数

2 α稳定分布噪声特性及产生方法

α稳定分布噪声特征函数表达式[27-28]为：

φ(t)=

(4)

式中：特征指数α∈(0,2]，α值越小，噪声脉冲特性就越强，而拖尾特性则相反，如图3所示。对称参数β∈[-1,1]，决定了分布的对称性。当β=0时，噪声是呈对称分布的，β≠0时，分布中心向左或向右偏移。尺度参数σ∈[0,+)，是度量样本值相对于均值的分散程度。位置参数μ∈(-,+)，决定了分布的中心。

(a)α=0.8

本文α稳定分布噪声的随机变量X采用CMS(Chambers-Mallows-Stuck)算法[29]产生。

当α≠1时，

(5)

式中:V,W为独立随机变量，V服从(-π/2,π/2)上均匀分布，W服从均值为1的指数分布，且Cα,β和Dα,β,σ表达式为：

(6)

Dα,β,σ=σ[cos(arctan(βtan(πα/2)))]-1/α

(7)

当α=1时，

(8)

3 数值解析方法

本文采用四阶Runge-Kutta算法[30]对式(1)进行求解，具体步骤如下：

k1=h[-ax(n)+bx3(n)-

cx5(n)+rx2(n)+s(n)],

k4=h[-a(x(n)+k3)+b(x(n)+k3)3-

c(x(n)+k3)5+r(x(n)+k3)2+s(n+1)]

(9)

式中:s(n)与x(n)分别是输入和输出信号第n次采样值，ξ(n)为α稳定分布噪声第n次采样值，h为时间步长。由于α稳定分布噪声具有特征指数α越小，脉冲特性越强特征，导致粒子跳跃距离趋向无限大。因此，在数值仿真时需要对输出信号x(t)进行人为限幅[31]，为了实现更好的共振效果，本文采取的限幅措施为：当|x(t)|>2时，令x(t)=sign(x(t))×2。

4 系统性能指标

描述一个系统共振效应的性能指标有很多，其中应用最广泛是信噪比(SNR)和信噪比增益(SNR Improvement,SNRI)。SNRI比SNR更能直接反应出输出信号相对于输入信号品质改善程度，当SNRI>1时，说明待测信号在通过随机共振系统后能量得到了增强。并且SNRI越大，系统对输入信号增强和改善作用越好。SNRI定义为输出SNR和输入SNR的比值[32,33]，其表达式为：

(10)

式中:Pin与Pout分别为系统输入和输出总功率，Sin(f0)与Sout(f0)分别为系统输入和输出信号功率。

为了减少SNRI随机性，本文采用平均信噪比增益(Average-SNRI,A-SNRI)来衡量系统的性能，其定义为：

(11)

式中:n为仿真次数，本文中n取50次，SNRIi为第i次仿真的信噪比增益。

5 α稳定分布噪声环境中非对称三稳系统的微弱信号检测与参数诱导的随机共振

取式(1)中待测信号A=0.5，f=0.03，α稳定分布噪声参数α=1，β=0，σ=1，μ=0，放大系数D=0.2，采样频率fs=5 Hz，取样点数N=10 000。当系统参数a=0.3，b=1.3，c=1，偏度r=0.1，通过仿真实验得到结果,如图4所示。

(a)系统输入时域图

图4(a)是加α稳定分布噪声的待测信号时域图，图4(b)是对应的FFT变换得到的频谱图。由4(a)与(b)可以观察到，待测信号淹没在噪声中，不能有效提取有用信息。将含噪待测信号输入非对称三稳系统，然后调节系统参数a和b，当a=0.3，b=1.3时，系统输出时频图如图4(c)和(d)所示。由于α稳定分布噪声的尖峰脉冲特点，所以在图4(c)不能观察到输出信号的时域信息。从图4(d)中可以清晰看到有一个显著的尖峰值，且该值对应的频率0.03 Hz正好是待测信号的频率，说明待测信号能被检测出来且幅值被放大了，这是由于通过调节系统参数改变了势垒高度，使得粒子有足够能量越过势垒，在不同势阱间往返跃迁运动，此参数条件下，待测信号、噪声和非对称三稳系统间实现了较好匹配，发生了随机共振现象。因此，通过调节参数，非对称三稳系统能产生随机共振，达到α稳定分布噪声环境中微弱周期信号检测目的。

接下来将深入研究α稳定分布噪声中，特征指数α与对称参数β分别取不同值条件，非对称三稳系统结构参数a，b，偏度r和噪声放大系数D与非对称三稳系统随机共振输出效应作用规律。

5.1 不同特征指数α下的随机共振

5.1.1 不同特征指数α下A-SNRI随参数a的变化

令特征指数α分别为0.7，1，1.3，其余噪声参数分别为β=0，σ=1，μ=0。待测信号，采样频率及采样点数保持不变，固定参数b=1.3，c=1，r=0.1，D=0.2，通过仿真实验得到A-SNRI随参数a的变化规律如图5所示。从图5(a)可以看出，当α取0.7，1和1.3时，随着a的增大，A-SNRI整体先增大后减小，且当α=1，a=0.3，A-SNRI最大，此时待测信号、噪声和非对称三稳系统之间实现了较好匹配，噪声转移到信号的能量最大，达到了更佳共振效果。并且，随着a的继续增大，系统响应时间过长，使得这种较好匹配关系被打破，A-SNRI逐渐下降，系统性能也大幅下降。此外还观察到，共振效果较好区间不随α变化而改变，并且当α=1时A-SNRI最大。由图5(b)与(c)可以看出，当α<1时，随着α增加，A-SNRI越来越大，当α>1时，随着α增加，A-SNRI越来越小，产生此现象的原因，在5.1.2节解释。

(a)不同α下A-SNRI随a的变化

5.1.2 不同特征指数α下A-SNRI随参数b的变化

固定a=0.3，令r=0.1，D=0.2，其余参数与前面保持一致，通过仿真实验得到A-SNRI随b的变化规律如图6所示。由图6可以看出，A-SNRI随b是非线性变化的，且存在一个合适值b使得A-SNRI最大，即此时随机共振效果更好，对信号检测能力更强。当α=1时，A-SNRI最大，α<1，随着α减小，α稳定分布噪声的脉冲特性越强，导致粒子跳跃距离趋向无限大，所以A-SNRI越来越小。α>1，随着α增大，A-SNRI越小，说明α并不是越大越好，它存在一个合适值使A-SNRI最大，这与图5(b)与(c)的结论一致。

(a)不同α下A-SNRI随b的变化

5.1.3 不同特征指数α下A-SNRI随参数r的变化

固定参数a=0.3，b=1.3，令D=0.2，其余参数与前面保持一致，仿真得到A-SNRI随参数r的变化规律如图7所示。由图7可知，当α不相同时，都存在一个值r使A-SNRI在该α下最大，且当α=1，r=0.1时，A-SNRI最大，此时产生较好共振，信号检测效果更佳，这是因为不仅参数a和b能改变势函数形状，偏度r也能改变形状，使粒子能够越过势垒，进而影响系统共振效果。

图7 不同α下A-SNRI随r的变化

5.1.4 不同特征指数α下A-SNRI随噪声强度放大系数D的变化

固定a=0.3，b=1.3，r=0.1，其余参数与前面保持一致，仿真得到A-SNRI随D的变化规律如图8。从图8可以看出，随着系数D的增大，A-SNRI先增大后减小，这是由于刚开始随着D的增大，噪声能量转移到信号上的能量逐渐增强，当A-SNRI最大时，此时转移到信号的能量最大，随着D的继续增大，噪声干扰太强，信号被噪声淹没，因此A-SNRI越来越小。随着α增大，粒子需要更多的能量才能越过势垒实现阱间跃迁，所以随着α的增大，A-SNRI的峰值向右移，且当α=1时，A-SNRI峰值最大，共振效应较好区间不随α的变化而发生改变，说明系数D的较好共振区间不受α变化的影响。

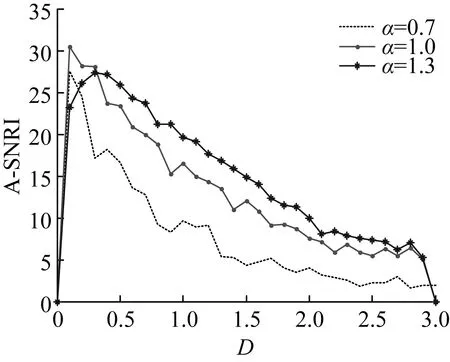
图8 不同α下A-SNRI随D的变化

5.2 不同对称参数β下的随机共振

对称参数β分别取-1，0，1，其余噪声参数分别取α=1，σ=1，μ=0。待测信号，采样频率及采样点数均保持不变，固定参数b=1.3，r=0.1，D=0.2，通过仿真实验得到不同β下A-SNRI随参数a的变化规律如图9所示。由图9可知，与前面不同α下A-SNRI随参数a变化规律相同，即不同β下A-SNRI随参数a呈先增后减趋势，表明参数a的变化降低了势垒高度，使得粒子发生跃迁所需能量较低，粒子的能量达到了跃迁需求，从而实现了随机共振。发生随机共振现象较好区间不随参数β变化而变化，且在区间[0,2.5]时，β=-1与β=1时曲线大致相同，β=0时A-SNRI峰值大于β≠0时的峰值，说明参数β的改变对参数a产生较优A-SNRI的区间无影响，这对参数的合适选取具有参考价值，且α稳定分布噪声呈对称分布(β=0)时A-SNRI最大。

图9 不同β下A-SNRI随a的变化

图10是β分别取-1，0和1时，固定参数a=0.3，r=0.1，D=0.2，其余参数不变得到的A-SNRI随参数b变化规律曲线。从图中可以观察到，β取不同值时，A-SNRI随b的变化与前面不同α时随b变化规律是一样的，因此这里将不再详细描述。

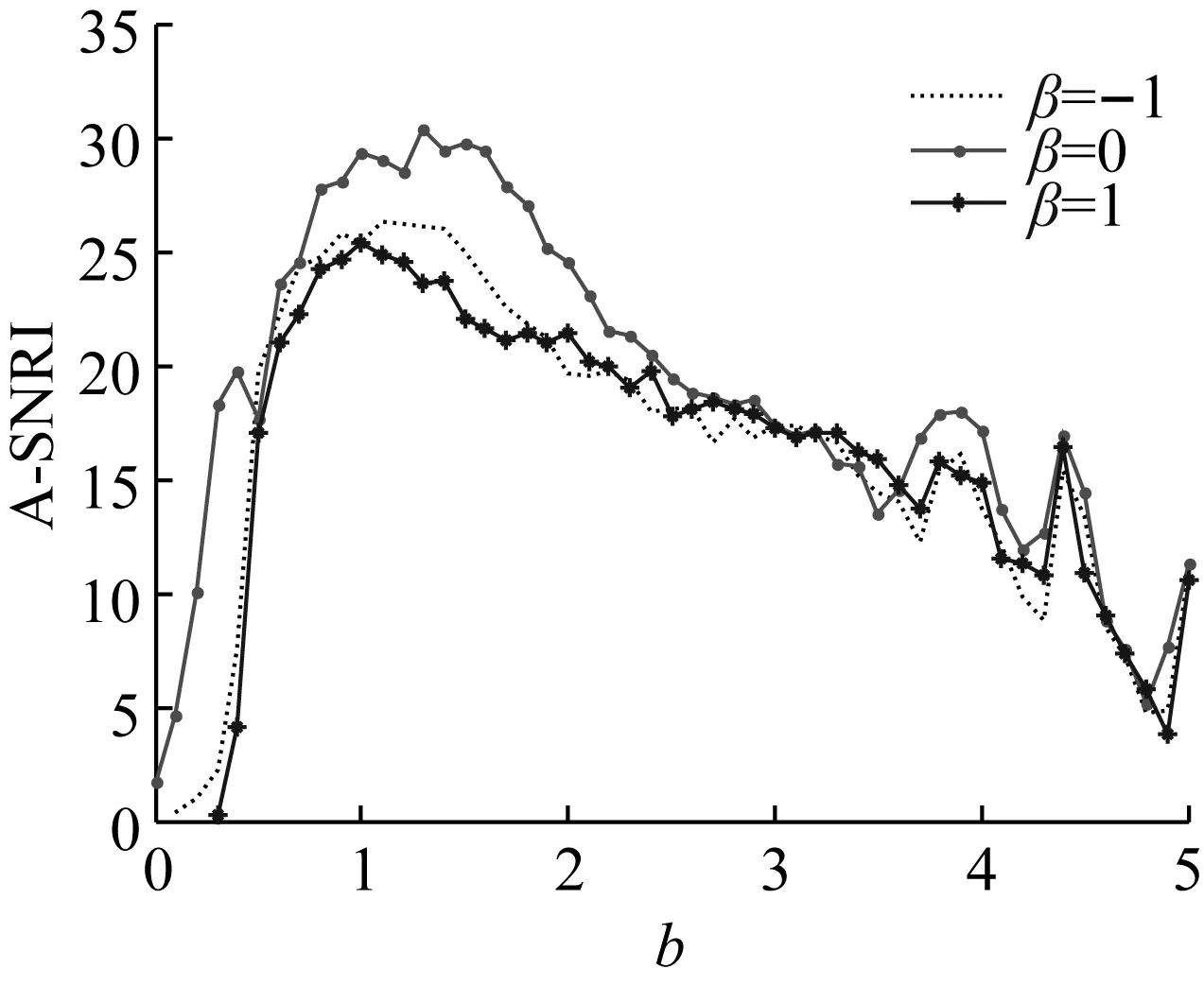
图10 不同β下A-SNRI随b的变化

图11是固定参数a=0.3，b=1.3和D=0.2得到的A-SNRI随偏度r变化规律图，从图中可以观察到，不同β下A-SNRI随r非线性变化，并且存在一个最大值。A-SNRI最大，说明在此参数条件下随机共振效应更好。由于当β=0时，α稳定分布噪声是呈对称分布的，β>0时，分布中心向左偏移，β<0时，中心向右偏移，图11中A-SNRI的峰值在β≠0时的偏移现象与噪声分布是对应的，且只有当噪声呈对称分布时，A-SNRI才最大，此时系统性能更好。

图11 不同β下A-SNRI随r的变化

图12是固定参数a=0.3，b=1.3，和r=0.1得到的A-SNRI随强度系数D变化关系图。从图中可以观察到，当D逐渐变大，A-SNRI出现先增后减趋势，呈现非线性特征，A-SNRI存在峰值，说明系统产生了随机共振现象。共振效果相对较好区间不随β变化而改变，并且β=0时A-SNRI大于β≠0时A-SNRI，进一步验证了噪声呈对称分布时，共振效果更好。

图12 不同β下A-SNRI随D的变化

6 结 论

本文研究了α稳定分布噪声中非对称三稳系统的随机共振特性，当α稳定分布噪声参数α和β为不同值条件，从系统结构参数a、b，刻画系统偏度r和噪声强度放大系数D这几个方面详细分析了A-SNRI随a、b、r和D变化规律，通过研究分析得出以下结论：

(1)不仅系统参数a、b能改变势函数形状，偏度系数r也能改变势函数形状，从而影响系统随机共振性能，当r>0时，势函数向右偏，右边势阱加深，左边势阱变浅，当r<0时，势函数向左偏，左边势阱加深，右边势阱变浅，当r=0时，退化为传统对称三稳势函数形状；

(2)调节系统参数，当参数a=0.3，b=1.3，r=0.1，D=0.2时，系统能产生随机共振现象，实现α稳定分布噪声环境中微弱周期信号检测；

(3)当α稳定分布噪声参数α、β分别取不同值时，调节系统结构参数a、b，偏度系数r和D都能诱导产生随机共振；

(4)对任意一个参数a、b、r或D，A-SNRI都出现先增大后减小的趋势，且A-SNRI较优区间不随α或β的变化而改变；

(5)当特征指数α不同时，在任一参数a、b、r或D随机共振区间中，α=1时对信号检测效果更好，当α>1时，随着α增大，A-SNRI逐渐减小，当α<1时，随着α增大，A-SNRI逐渐增大；

(6)当对称参数β不同时，在任一参数a、b、r或D随机共振区间中，β=0时对信号检测效果较好，说明了α稳定分布噪声呈对称分布时系统对信号检测能力更好，且当β=-1时，A-SNRI峰值向右移，当β=1时，峰值向左移。以上结论对研究非对称三稳系统随机共振现象时合理选择参数范围实现自适应随机共振奠定了基础，有助于实际应用中对微弱信号的检测。

本文研究了α稳定分布噪声环境下非对称三稳系统的随机共振作用规律，将非对称三稳系统应用在实际轴承故障检测中，以及对系统参数的选取采用自适应优化算法，实现更好检测效果是接下来研究的方向。