基于幂次混合趋近律的Buck变换器滑模控制方法研究
2021-02-05刁冠勋代运滔
刁冠勋,代运滔
(1.国网上海市电力公司检修公司,上海 200063;2.遵义供电局,贵州 遵义 563000)
随着工业化程度不断提高,用电设备飞速发展,对电能质量提出更高要求。开关变换器作为电能转换重要的一环,受到国内外学者的普遍关注。尤其降压(Buck)变换器,由于在体积、重量和能耗等方面的优势,被广泛应用于航空航天、电动汽车、全电舰船等高新领域[1-4]。
Buck变换器输出电压及电流谐波含量越低,波形越平滑,电能质量越好。高性能控制算法无疑会提高Buck变换器输出的电能质量[5]。滑模变结构控制算法对系统外部扰动和内部变化具有强鲁棒性,能较好地应用于Buck变换器。文献[6]针对Buck变换器传统PI控制动态响应和抗干扰能力差等缺点,提出一种鲁棒离散积分滑模电压控制方法,提高输出电压的动态品质和抗扰性,抑制了滑模抖振。文献[7]针对Buck变换器滑模系数难以确定、动态响应和鲁棒性难以同时提高等缺点,提出一种电感电流自适应终端滑模控制方法。通过李雅普诺夫求解系数,构建非线性环节,实现双闭环滑模控制方法,解决了上述不足。
作为滑模控制算法重要组成部分,趋近律控制方法通过设计趋近律表达方式,调节系统到达滑模面动态性能,进而缩短Buck变换器输出电压到达稳态作用时间,减小超调量[8]。文献[9]针对传统等速趋近律趋近时间较长、抖振严重等情况,提出一种新型趋近律控制方法。该方法提高系统趋近速度,抑制滑模抖振,仿真结果证明了该方法的有效性。为补偿Boost变换器非线性滑模等效和实际控制之间的误差,文献[10]提出一种新型趋近律,使系统状态在远离和靠近滑模面时,均能保持较快趋近速度,减小滑模抖振。文献[11]通过引入滑模参数和系统状态,重新设计趋近律参数,并采用幂次函数取代开关函数,加快Buck变换器动态响应,减小超调量。
在上述文献基础上,本文针对Buck变换器,提出一种新型幂次混合趋近律控制方法。通过对趋近律参数进行自适应调节,进一步提高系统收敛速度,减小抖振。
1 Buck变换器状态方程
Buck变换器又称降压变换器。通过开关管通断,将变换器输入电压转换为低输出电压,以供用电设备使用。Buck变换器拓扑结构如图1所示。
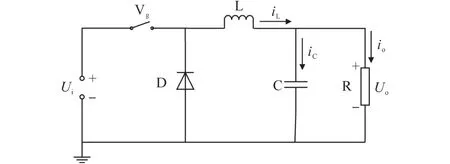
图1 Buck变换器拓扑结构Fig.1 Buck converter topology
图1中,变换器输入电压、输出电压分别用Ui和Uo表示。假设Buck变换器带线性负载R,主体结构由开关管Vg、二极管D、电感L、电容C组成。当开关管Vg导通时,电流通过电感L,流到电容C和负载R,电感L和电容C分别起滤波和储能作用。此时二极管承受反向电压关断。当开关管Vg关断时,二极管承受正向电压导通,电感L电流不能立刻降为零,起续流作用,同时电容C释放存储电能给负载R。通过快速通断开关管,输出电压Uo能稳定于参考电压Uref。定义u=1为开关管Vg导通,u=0为开关管Vg关断,因为电感L和电容C均为储能元件,以电感电流iL和输出电压Uo为状态变量,求得状态方程如下:

以式(1)为基础,进一步求解Buck变换器二阶状态方程。定义Buck变换器输出电压误差x1=Uref-Uo,输出电压误差变化率根据系统状态,可得Buck变换器二阶状态方程为
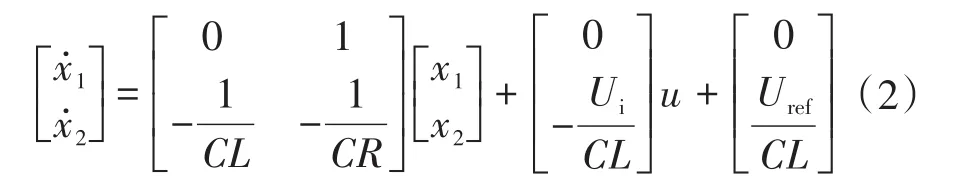
式(2)状态方程为非线性,滑模控制同样为典型的非线性算法,非常适合应用于式(2)的方程。对于滑模控制算法,滑模面选取至关重要,本文选用线性滑模面如下式:
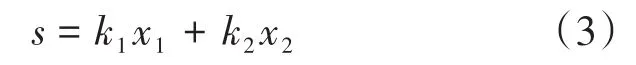
其中,滑模面参数k1>0,k2> 0。对式(3)求导,并将式(2)代入,可得开关管Vg控制作用u为
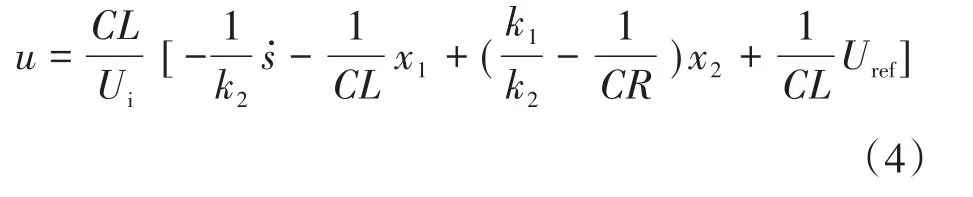
式中:为幂次混合趋近律。
2 Buck变换器滑模控制方法设计
2.1 幂次混合趋近律提出
高为炳院士最早提出趋近律控制方法[12]。指数趋近律设计简单,应用最广,其数学表达式为

当系统从初始位置s(0)运行至滑模面s(t)=0时,求得到达时间为
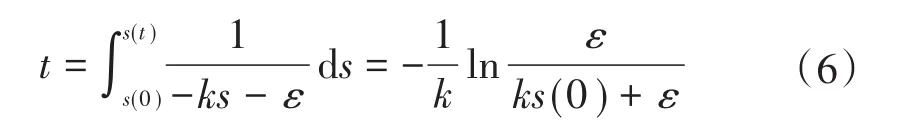
初始位置s(0)<0运行至滑模面作用时间以此类推。从式(6)可以看出,在初始位置不变的情况下,到达时间与趋近律参数k和ε有关,与系统数学模型无关。到达时间保持不变,是指数趋近律最大的优点。但指数趋近律缺点明显,无法真正意义上消除系统抖振。
为克服指数趋近律的缺点,文献[13]提出一种变指数趋近律:
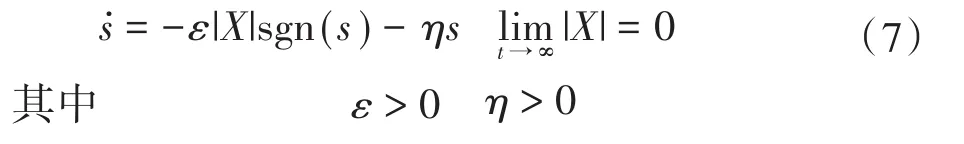
式中:X为系统状态。
相比指数趋近律,变指数趋近律能加快系统趋近速度,在距离滑模面较近时,随系统状态大小调节趋近速度,最终收敛于平衡点。但变指数趋近律有两大不足:1)距离滑模面较远时,系统趋近速度没有幂次趋近律快;2)当到达滑模面,系统状态较大时,趋近速度较快,超调量较大。
针对以上两点不足,本文在变指数趋近律基础上,提出一种新型幂次混合趋近律,表达形式如下:
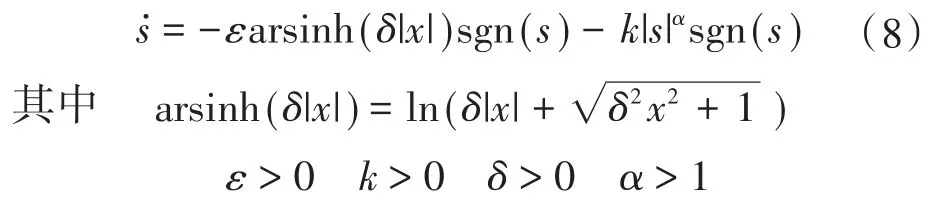
式中:sgn(s)为符号函数;x为系统状态;arsinh(δ|x|)为反双曲正弦函数。
arsinh(δ|x|)根据系统状态x自适应调节趋近速度,曲线如图2所示。
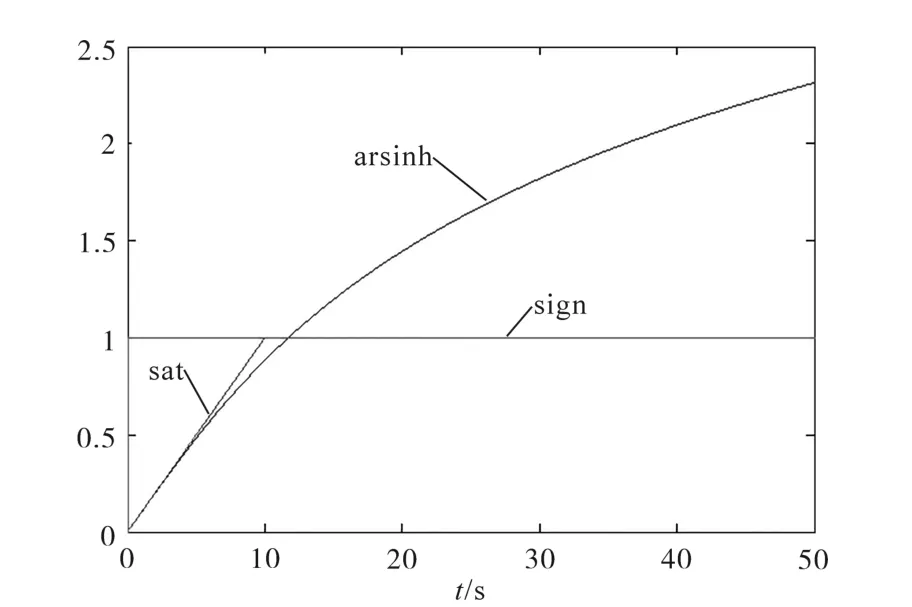
图2 三种函数曲线比较(δ=0.1)Fig.2 Comparison of three function curves(δ=0.1)
从图2中可以看出,系统状态较大时,arsinh具有比符号函数sign和饱和函数sat更快的收敛速度;系统状态靠近滑模面时,arsinh收敛速度变缓,且曲线光滑性更好,能减少超调量,减小系统抖振。
幂次混合趋近律由-εarsinh(δ|x|)sgn(s)项和-k|s|αsgn(s)项组成。通过以上分析,当系统距离滑模面较远时,-k|s|αsgn(s)项起主要作用,与-εarsinh(δ|x|)sgn(s)项共同作用,维持较快的趋近速度。当系统距离滑模面较近时,-k|s|αsgn(s)项由于幂次项,趋近速度呈几何倍速放缓。-εarsinh(δ|x|)sgn(s)项起主要作用,且趋近速度随系统状态减小而减小,自适应调节滑模抖振,直到系统最后收敛于平衡点。
切换带能调节系统到达滑模面的抖振大小。由上文分析,幂次混合趋近律到达滑模面的抖振大小,主要由 -εarsinh(δ|x|)sgn(s)项决定。系统到达滑模面,趋近平衡点过程中,若平衡点附近x=0+→x=0,则
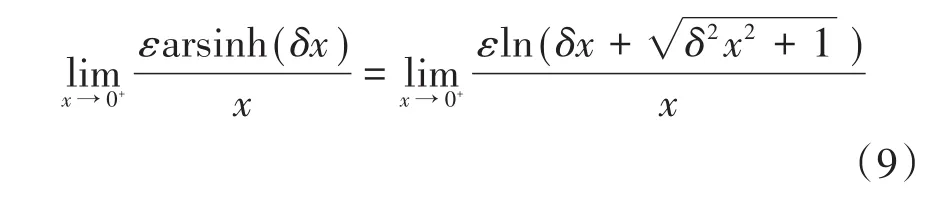
对分子、分母求导,得:
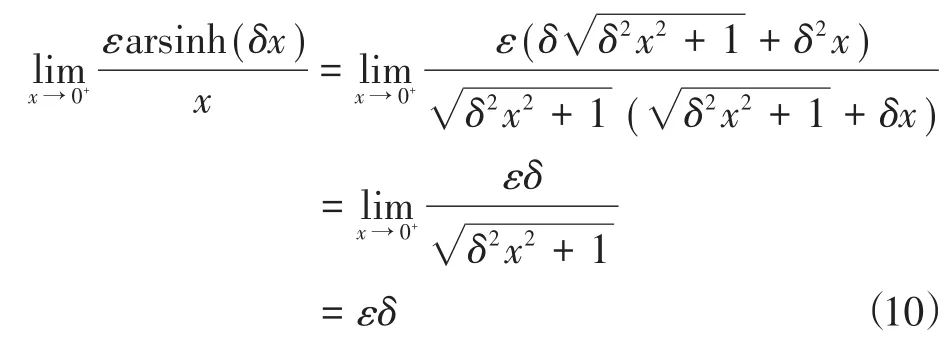
同理,若平衡点附近x=0-→x=0,则
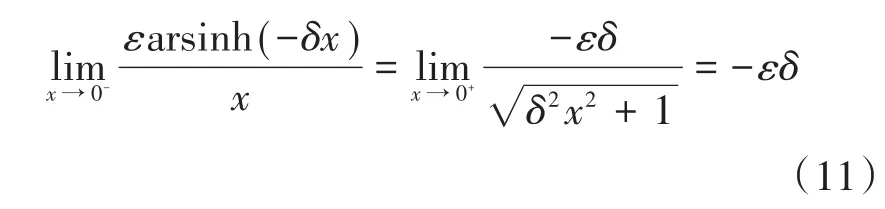
根据式(10)、式(11),系统到达滑模面后的稳态性能由参数ε,δ决定,尤其平衡点附近抖振,由参数ε和δ的乘积决定。
本文提出的幂次混合趋近律控制方法,有效克服文献[13]变速趋近律不足。首先,引入幂次项,有效提高系统趋近速度。其次,当到达滑模面,系统状态较大时,arsinh(δ|x|)arsinh(δ|x|)项有效降低系统状态大小,进而减小超调量。
2.2 控制性能分析
滑动模态成立的前提是满足到达条件,定义李雅普诺夫(Lyapunov)函数为

对式(12)求导,得:
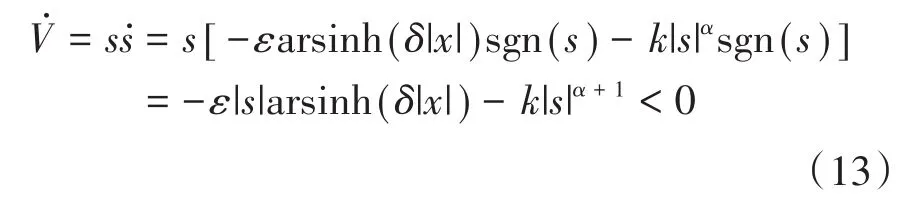
由式(13)可知,本文设计的幂次混合趋近律控制方法满足到达条件。
Lyapunov稳定性条件只是定性分析幂次混合趋近律控制方法有效性,下面对到达时间进行定量分析。
1)若系统状态s(0)>0,则式(8)化为
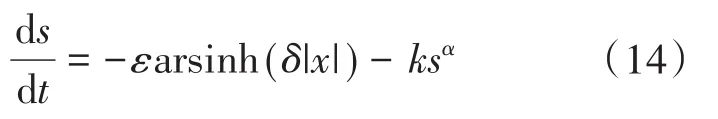
系统从初始状态第1次到达滑模面s(t)=0的作用时间为

由上文分析,距离滑模面较远时,-k|s|αsgn(s)项起主要作用;距离滑模面较近时,-εarsinh(δ|x|)sgn(s)项起主要作用。两者以s=1为分割点,则式(15)变为
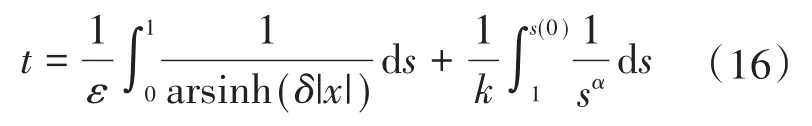
由于 arsinh(δ|x|)是递增函数,在s(0)→0 过程中,|x|∈ [xmin,xmax],则

2)若系统状态s(0)<0,推导方法依次类推。
由此可见,采用幂次混合趋近律控制方法,系统能在一定时间内到达滑模面。
2.3 比较验证
为验证幂次混合趋近律控制方法的快速性和稳定性,与指数趋近律和幂指数趋近律进行比较,并应用于二阶系统:
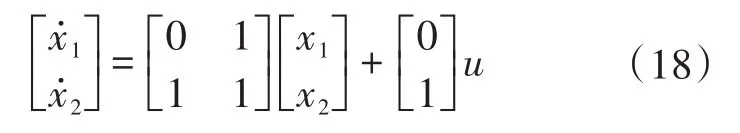
初始状态为[20,0]T,滑模面如式(3),k1=10,k2=1。三种趋近律参数分别如下:
1)幂次混合趋近律:趋近律表达式见式(8)。
2)指数趋近律:

3)幂指数趋近律:
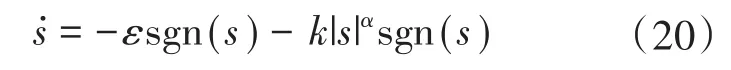
参数取k=10,ε=10,α=2,δ=0.2,滑模面s如图3所示,系统状态x1,x2分别如图4、图5所示。
通过比较指数趋近律和幂次指数趋近律,|s|α项有效提高系统趋近速度;通过比较幂指数趋近律和幂次混合趋近律,arsinh(δ|x|)项减少了超调量,随着系统状态自适应调节滑模抖振,最终收敛于平衡点。通过式(17),计算系统从初始状态到滑模面作用时间t<0.1 s+0.2 s,符合图3系统到达滑模面时间,印证了计算方法的有效性。
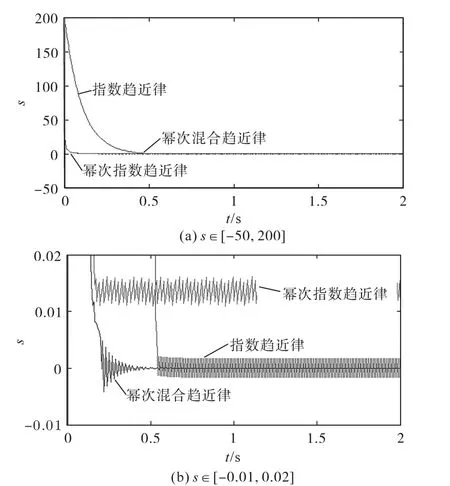
图3 滑模面sFig.3 Sliding surface s
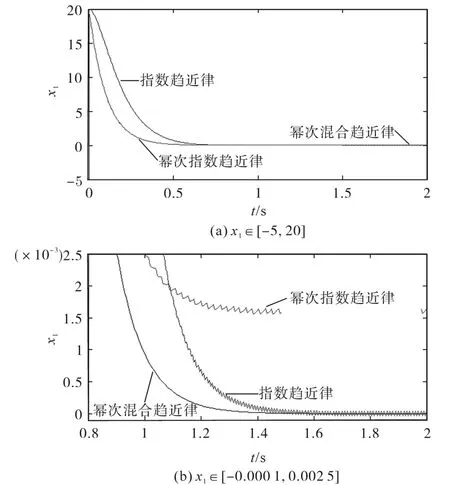
图4 系统状态x1Fig.4 System status x1
2.4 二阶控制器设计
滑模控制算法对外部干扰和参数变化具有极强的鲁棒性。理想的Buck变换器输出电压最终收敛于Uref,但实际滑模控制中,时延和滞后等干扰会产生误差。定义误差为d,则滑模面s变为
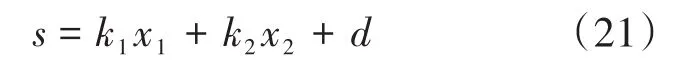
当系统到达滑模面,求得系统状态为

由此可见,当存在误差d时,系统状态最终收敛于-d/k1。增大k1能减少Buck变换器的稳态误差,但过大的k1会造成输出电压超调量较大。
根据李导数定义,求得等效控制ueq为
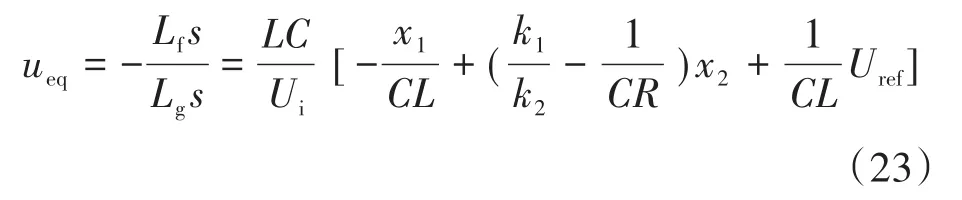

当k1/k2=-1/CR时,等效控制ueq不再受输出电压变化率影响,此时等效控制ueq=Uo/Ui。综上,对滑模面参数k1,k2取值时,应该先确定k1值,进而通过比例关系,求得k2值大小。
将式(8)代入式(4),求得开关管Vg控制作用u为
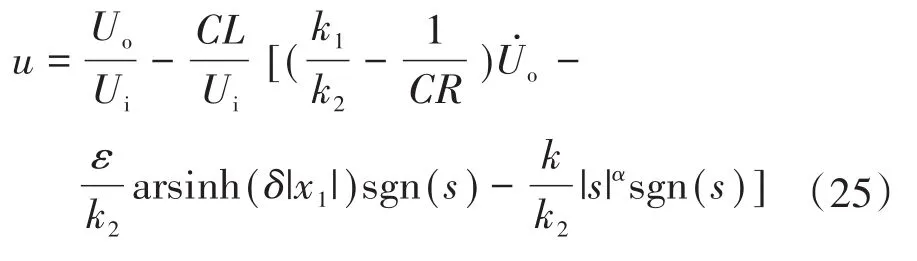

图5 系统状态x2Fig.5 System status x2
3 仿真和实验
为验证本文提出的Buck变换器幂次混合趋近律控制方法有效性,将其与指数趋近律控制方法进行比较,并搭建控制器Matlab/Simulink仿真模型。Buck变换器参数为:电容C=0.05 mF,电感L=0.75 mH,电阻R=10 Ω,输入电压Ui=36 V,参考电压Uref=20 V。滑模面参数:k1=200,k2=1。图6为基于两种趋近律控制方法的Buck变换器输出电压比较;图7为基于两种趋近律控制方法的Buck变换器电感电流比较。
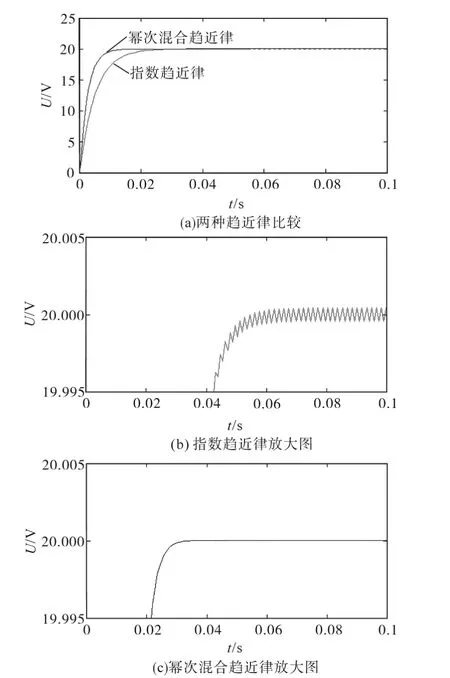
图6 Buck变换器输出电压Fig.6 Buck converter output voltage
从图6、图7可以看出,采用指数趋近律控制策略,输出电压到达稳态时间较长,超调量较大,稳态后波动较大。而采用幂次混合趋近律控制策略,输出电压到达稳态时间较短,超调量几乎为零,稳态后无波动。电感电流进一步证明控制策略的有效性。
为验证基于幂次混和趋近律的滑模控制器有效性,搭建实验平台将其与指数趋近律相比较。Buck变换器输入电压由可编程电源Chroma 6250P提供,输出电压范围0~600 V,选择36 V作为输入电压。二极管型号为STPS20200CT,电感型号为具有高额定电流的VLB12065HT-R36,大小为0.5 mH。电容型号为GRM32ER71H106MA12,采用2个10 μF电容并联。负载采用可编程电子负载Agilent 6060B。开关管采用TI公司的CSD16414Q5。图8为通电后,基于两种趋近律控制方法的输出电压实验波形比较;图9为稳态后,基于两种趋近律控制方法的输出电压实验波形比较。

图7 Buck变换器电感电流Fig.7 Buck converter inductor current
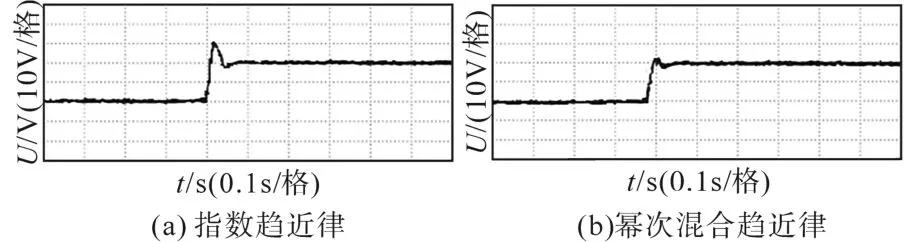
图8 通电后输出电压实验波形比较Fig.8 Comparison of output voltage experimental waveforms after power-on
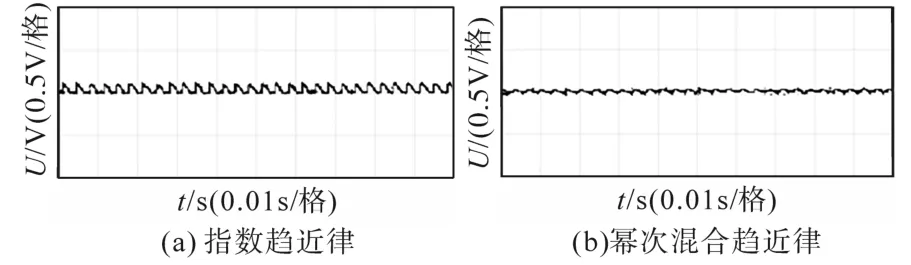
图9 稳态后输出电压实验波形比较Fig.9 Comparison of output voltage experimental waveforms after steady state
从以上实验图可以看出,相比于指数趋近律控制方法,本文提出的幂次混合趋近律控制方法输出电压动态调节时间更快,超调量较小,稳态后电压波动小,与仿真结果保持一致。
4 结论
本文在指数趋近律基础上,提出一种基于幂次混合趋近律的Buck变换器滑模控制方法。通过引入幂次函数和反双曲正弦函数,提高系统趋近速度,减少稳态误差,提高稳态性能。给出Buck变换器状态空间方程以及滑模控制器设计流程。本文提出的基于幂次混合趋近律滑模控制方法不仅用于Buck变换器,还能用于一般意义的非线性模型,例如永磁同步电机、机械臂等,具有较强的普适性。
