基于谐振式MMC的直流变压器设计
2021-02-05
(河南工学院电气工程与自动化学院,河南 新乡 453003)
高压直流(high voltage direct current,HVDC)输电的快速发展引起了对直流电网配电技术的研究热潮[1]。而模块化多电平变换器(modular multilevel converter,MMC)技术已在许多应用中实现[2],未来的演变趋势必然是一对多的电能变换形式。在中、高压应用中开发模块化DC/DC直流变换器具有重要意义[3]。高压应用场合中模块化直流变换器的研究集中于提高变换器性能[4],然而在保持低成本的同时考虑提高可靠性才是变换器研发的首要任务。
与高压应用的变换器相比,具有并联输入级联输出的直流变换器广泛应用于中压直流变压器[5]中,电力电子变压器除了适用于在配电网中[6],还可用于牵引系统[7]。直流变换器采用输入级联输出并联配置,要求对级联电压和并联电流进行强制均衡控制。对于高压应用,这种配置需要大量的隔离变压器,这会给均衡控制带来高复杂性,并且会因为变压器故障而导致高故障风险。
高压应用中,基于半桥或全桥子模块的MMC直流变换器通常无需变压器配置[8]。但传统谐振式MMC直流变压器的变比设置较大,且低压侧电流必须流过高压侧的功率半导体器件。为此,本文设计了一种新颖的谐振式MMC直流变压器,通过更灵活的调制方案,可实现宽范围变比,同时不需要额外的电压均衡控制。最后,对所研发的谐振式MMC直流变压器的性能进行了实验验证。
1 谐振式MMC直流变压器
具有N个子模块的单极谐振式MMC电路结构如图1所示。图1中,第j(j=1,2,…,N)个子模块的电容电压和输出电压分别用uCj和uj表示。所有子模块的电压叠加为us=u1+…+uj+…+uN。单极谐振式MMC电路的调制规则为:1)应充分利用子模块以保持低成本;2)子模块电压应低于2Udc/N,Udc为输入直流电压;3)子模块电容器电压应该是自平衡的,无需额外的均衡控制。第2条规则是第1条的扩展,可保证所有子模块都参与变换而降低成本,详见后文。
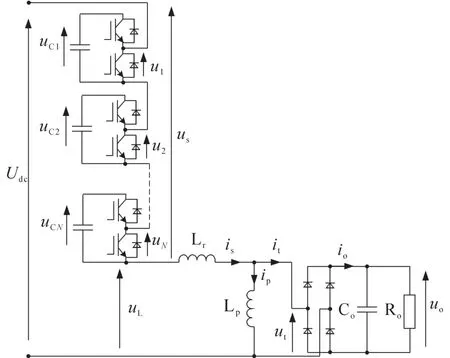
图1 单极谐振式MMC电路结构示意图Fig.1 Schematic diagram of monopole resonant MMC circuit
直流变压器通过叠加的子模块直流电压来支持输入直流高压,以及处理交流电压纹波。通过调制策略设计,可实现最少数量的子模块工作对应直流变压器最大变比,也就是说,us在N-1个子模块电容器电压之和与N个子模块电容器电压之和之间交替。假设级联的子模块电容器总数为X,不投入的子模块电容器总数量为Y(0<Y<X≤N),则当X=5和Y=4时,直流变压器的时域电压波形示意图如图2所示。
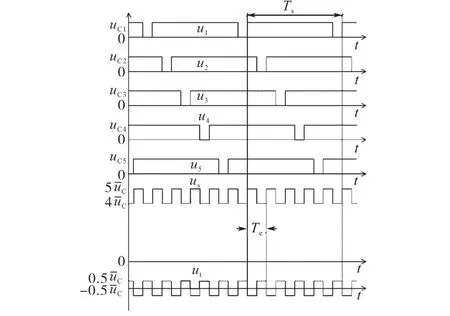
图2 当X=5和Y=4时的子模块电压波形Fig.2 Submodule voltage waveforms with X=5 and Y=4
值得注意的是,谐振式MMC的子模块开关动作与常规MMC不同,在谐振式MMC中,子模块的上下开关在一个周期中的导通时间不同。从图2中可以看出,每个子模块在1个周期Ts中只有1个互补脉冲。故整流器输入电压峰峰值为单个子模块电容器电压。为了简化分析,忽略桥臂电感的影响,该运行模式下的直流变压器的变比为2N-1。然而,对于HVDC链路而言,如果直流变压器变比范围更宽,则更为有利,而这可以在不改变电路配置的情况下通过改进调制策略来实现。改成第N-2~N个子模块调制后,变换器的变比将发生改变,如图3所示。图3中每个子模块输出电压uj在每个周期中具有2个互补脉冲。HVDC链路中Udc等于级联的N-1个子模块的电压,但输出电压等于1个子模块的电容电压,故直流变压器的变比减小到N-1。通过在子模块中施加更多互补脉冲可进一步降低直流变压器的变比。若采用第2~N个子模块调制,则变比变为(N+2)/(N-2)。若变换器使用1~N个子模块调制,则变比达到最低。
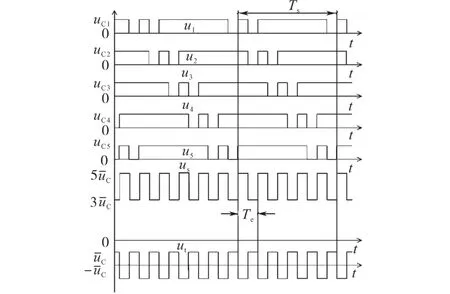
图3 当X=5和Y=3时的子模块电压波形Fig.3 Submodule voltage waveforms with X=5 and Y=3
谐振式MMC以谐振模式运行。不同变比下整流器电压ut具有相同的频率,谐振具有固定周期Te。单极谐振式MMC处于不同导通模式下的谐振回路电压和电流波形如图4所示。

图4 谐振回路电压和电流波形Fig.4 Voltage and current waveforms of the resonant tank
在固定的等效工作频率下,谐振式MMC工作在断续工作模式(discontinuous conduction mode,DCM)或连续工作模式(continuous conduction mode,CCM),或是DCM和CCM的组合模式。图4a中为谐振式MMC在DCM模式下谐振回路中的电压和电流波形。前半周期以ut=uo开始,其中is和ip已重叠。级联电流随着谐振波形开始上升,并在达到峰值后下降。在不到半个Te周期内,io下降到零。输出与并联电感Lp断开,此时ut取决于电流ip,级联电流下降到与并联电流重叠,直至前半周期结束。在该周期的后半部分期间,整流器的输入电压ut=-uo,级联电流开始谐振到其负峰值。在级联电流达到负峰值后,它开始上升并最终与并联电流重叠,其运行与先前分析的相同。图4b中为谐振式MMC在CCM模式下谐振回路中的电压和电流波形,图中整流器电流连续,而输入电压为完整方波。在前半周期中,级联电流谐振,直到整流器输入电压ut反转为-uo,整流器电流换向迫使级联电流与并联电流重叠。之后,级联电流在后半周期再次开始谐振,当ut再次反转为uo时,级联电流与并联电流重叠。
2 谐振式MMC直流变压器的运行分析
2.1 谐振式MMC的变比
变换器的平均子模块电压为
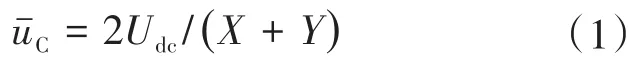
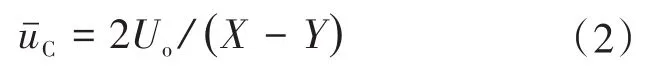
式中:Uo为负载侧电压。因此变比为

由式(3)可知,当X=N且Y=N-1时,可实现最大变比Udc/Uo=2N-1,当X=N且Y=1时,可实现最小变比Udc/Uo=(N+1)/(N-1)。需注意到,如果X<N,则存在子模块未被充分利用,在这种情况下,只需要X个子模块,且子模块数应减少到X而不是N。因此,根据第1个设计规则,为了保持低成本,应令X=N。基于式(1)和式(3),子模块电容电压与输入电压的比率与X和Y的关系如图5a所示(N=20),直流变压器变比与X和Y的关系如图5b所示(N=20)。
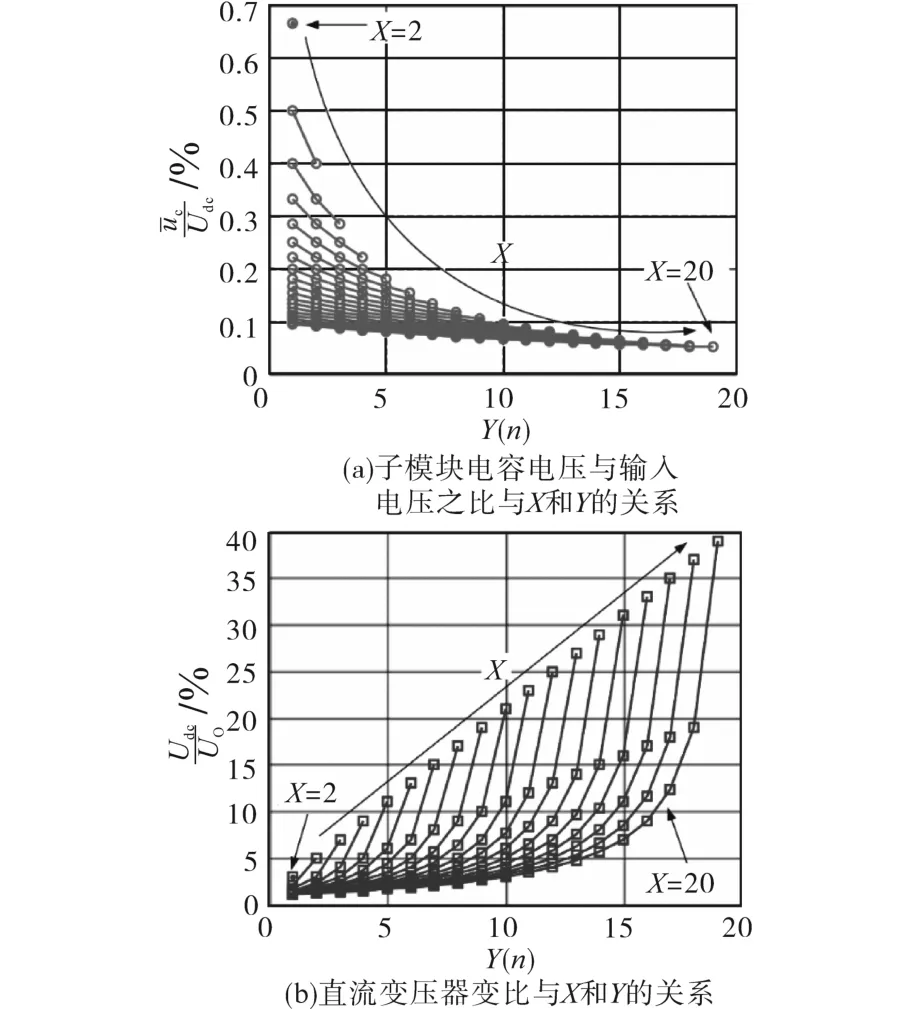
图5 电压比与X和Y的关系Fig.5 Relationship between voltages ratio and X and Y
从图5b中可以看出,X必须尽可能大,以充分利用子模块来承担HVDC链路直流电压。当X=N时,Y取值范围为从1~N-1的值,故通常设定X=N,变比范围为(N+1)/(N-1)~2N-1。
2.2 固有的电容电压平衡能力
谐振式MMC无需额外的电压均衡控制即可实现子模块电容器电压平衡。以图2调制策略为例(X=5和Y=4),有以下电压关系式:
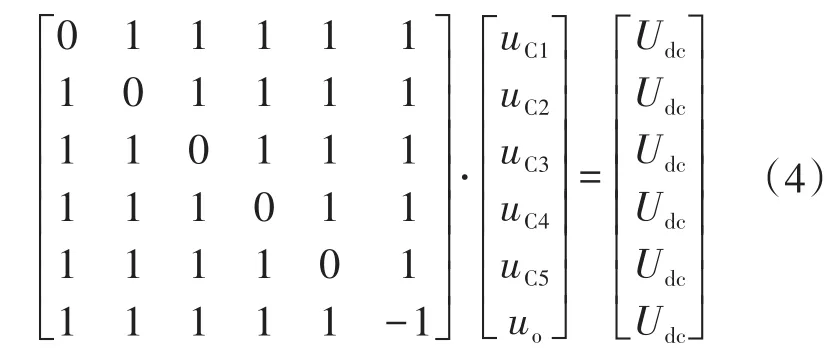
式中:uC1~uC5为5个子模块的电容电压。
式(4)具有唯一解,并且谐振式MMC自身是自平衡的。如果采用图3所示的调制策略(X=5和Y=3),则子模块电容电压为
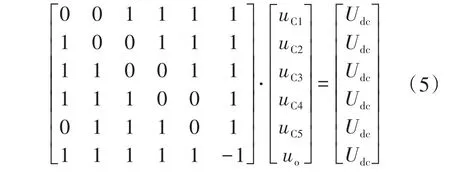
式(5)同样具有唯一解决,即子模块电容电压是自平衡的。类似地,如果设置X=5和Y=2或X=5和Y=1,子模块电容电压方程依然具有唯一解。因此,在X=5并且设置不同Y值的所有情况下,子模块电容器电压是自平衡的。此外,所有上述方程组都可用以下格式表示:

式中:A为不同调制策略(不同X和Y配置)。
如果等式(6)具有唯一解,即矩阵A满秩,则意味着子模块电容器电压是自均衡的。当X=5时,此条件始终满足。但当X变化时,A并不总是满秩。若X和Y设置不当,变换器可能会失去自平衡能力。图6所示为谐振式MMC的自平衡能力分析。从图6中可以看出,当设置Y=1和Y=X-1时,不论X取值如何,均具有自平衡能力,这是因为此时X和Y没有任何公约数,矩阵A满秩。此外,如果X是素数,则X和Y也没有公约数,矩阵A满秩,系统可自平衡。故推荐固定X为素数,改变Y来调节变比。
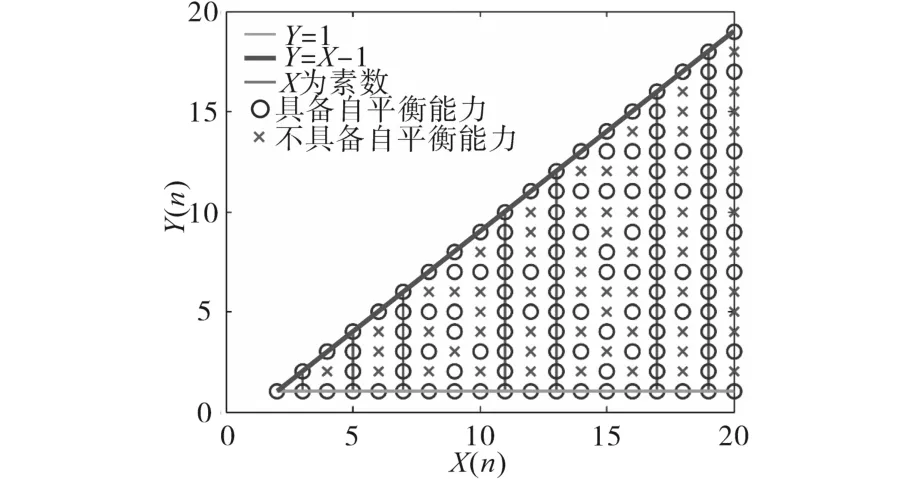
图6 自平衡能力分析Fig.6 Inherent-balancing capability analysis
3 高压应用设计实例
要将谐振式MMC直流变压器应用于高压系统,其设计过程必须遵循某些规定。用于HVDC的谐振式MMC具有与传统MMC类似的特征。但由于谐振式MMC与传统MMC的运行原理有很大不同,故应特别注意确保可靠性和兼顾经济性。
下面进行一项实例设计,单极谐振式MMC直流变压器额定功率4 MW,输入10 kV,输出4 kV,设置X=N,子模块由IGBT半桥模块和电容组成。子模块电容电压应低于0.67倍最大IGBT集电极-发射极电压UCES,如下式:

式中:UC为子模块电容电压;UCES为最大IGBT集电极-发射极电压。
由式(7)可知,谐振式MMC中子模块数量N由IGBT的电压UCES确定。考虑使用额定电压为3 300 V的IGBT,则N+Y≥10。另一方面,根据式(3)和10 kV至4 kV的变比可得:
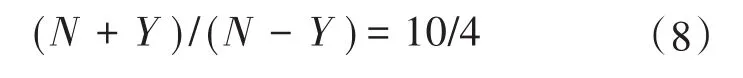
子模块电容器电压纹波应符合限制在±10%以内的要求。为了简化分析,使用粗略估计方法。假设桥臂电流包含有直流和交流分量,并且交流分量具有与整流器输入电压有相同的相角。在子模块输出电压持续高的时间内,电容在桥臂电流变为正时开始充电,在桥臂电流下降到零时结束充电。在开关周期其余时间内,电容放电。因此,可通过计算能量累积来近似能量峰峰值偏差,即

式中:ΔE为能量峰峰值偏差;Te为开关周期;P为平均功率;pdc,pac分别为瞬时直流功率和瞬时交流功率。
另一方面,子模块能量累积与电容器的平均电压的增加有关,其由下式给出:
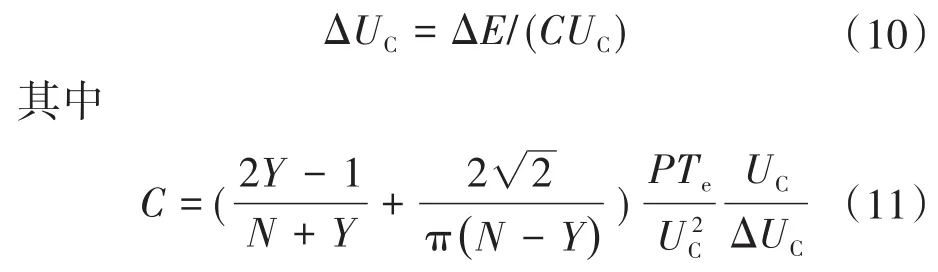
式中:C为子模块的电容器的容值。
取Te=1/1 400 s,Ts=0.01 s,因此,在ΔUC/UC<0.2的限制下,最终子模块电容容值选择为C=3 mF。
负载阻抗可用于估算电感。由于整流器输入电压为方波,峰值4 kV,电流均方根值1 kA。因此,负载阻抗为4 Ω,级联电感的阻抗不应超过负载阻抗的15%。开关频率为1.4 kHz时,级联电感选择为Lr=40 μH。并联电感器的设计需折衷考虑电压调节能力和峰值电流,故选择为Lp=700 μH。
图7为所设计的4 MW谐振式MMC直流变压器的仿真波形,其中整流器电压是频率为1.4 kHz的方波。级联电流在CCM模式下谐振,并且在整流器换向时与并联电流重叠。级联和并联电流共享直流分量,如图7a所示。is的直流分量和直流电压可计算输入直流功率;is的交流分量与整流器电压ut一起构成交流电源输出。输出直流电压为4 kV,纹波小于5%,如图7b所示。子模块电容器的电压波形为图7c,平均值2 kV,纹波±10%。
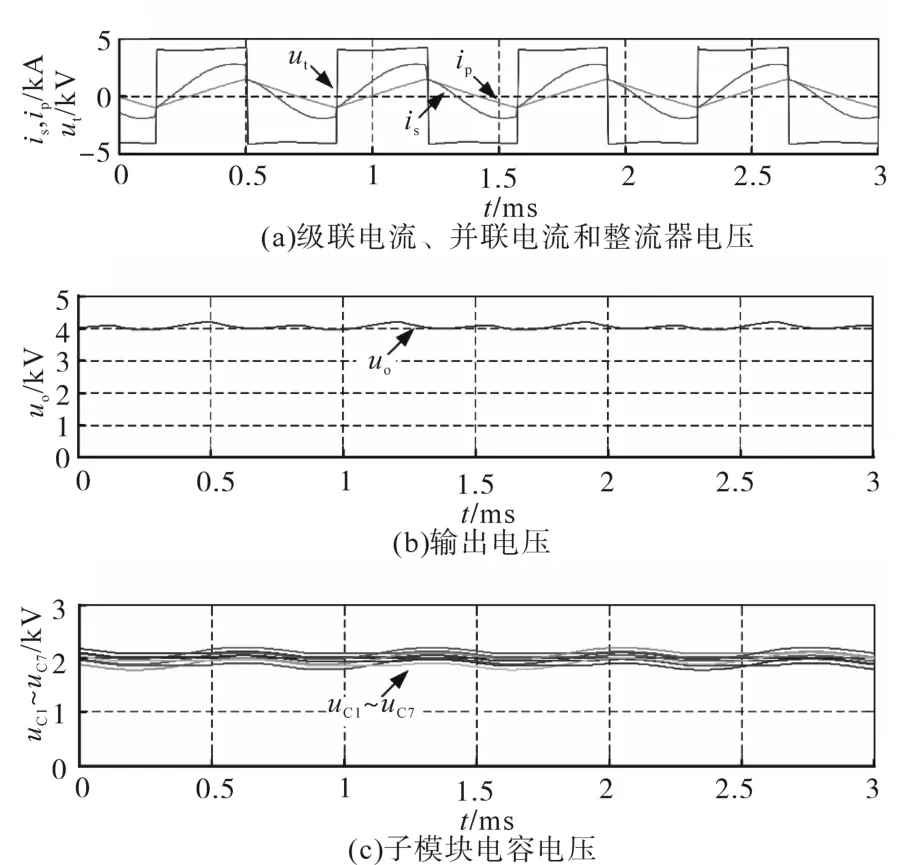
图7 4 MW直流变压器的仿真结果Fig.7 Simulation results of the 4 MW DC transformer
4 实验验证及结论
为了验证谐振式MMC直流变压器设计,在实验室搭建了具有5个子模块的小功率原理样机并进行了实验研究,实验平台如图8所示,电量数据采用KEYSIGHT公司的示波器DSOX1014A采集,控制器采用TI公司的数字信号处理器TMS320F28335,子模块采用英飞凌公司的半桥模块FF150R12ME3G。级联电感和电容放置于并联电感和整流器之间。详细的电路参数为:输入直流电压Udc=300 V,子模块电容容值C=49 μF,并联电感Lp=3 310 μH,输出电容Co=175 μF,级联电感Lr=331 μH,子模块数n=5。

图8 实验平台Fig.8 Experimental setup
图9所示为配置X=5和Y=4时的整流器输入电压ut、桥臂电流is波形、子模块输出电压u1和桥臂电流is波形。图9a、图9b和图9c中谐振式MMC的等效工作频率分别为3 kHz,3.5 kHz和4 kHz,对应子模块开关频率为600 Hz,700 Hz和800 Hz。图9a中直流变压器处于DCM模式,等效工作频率3 kHz。图中所示,当整流器电流为零时,其电压ut受到影响,这是由并联电感和整流器电容之间的谐振引起的。将等效工作频率增加至3.5 kHz,则工作在DCM模式和CCM模式的切换边界处,如图9b所示。进一步将工作频率增加到4 kHz,则完全在CCM模式下运行。在每半个工作周期结束时,桥臂电流被迫流过并联电感,整流器输入电流被迫换向,这可以从图9c中观察到。相对于工作频率,直流变压器的开关频率是非常低的。由于承受直流链路电压的子模块电容数量从4变为5,所以总级联电容的变化并不明显,如图9所示。故正半周期中的桥臂电流波形与负半周期中的桥臂电流波形没有太大差别。
图10a所示为工作频率为3.5 kHz时的整流器输入电压ut、桥臂电流is、子模块电容电压uC1和并联电流ip的实验波形。其中ip为三角波,且斜率随ut变化。输出电流io和输出电压uo如图10b所示,图中ut作为参考,uo接近子模块电容电压的50%。图10c为子模块上开关电压uSW1和电流iSW1的实验波形,图中波形表明上下开关均为零电压开关。
图11所示为配置X=5和Y=3,以及X=5和Y=1时的ut和is波形。图11a中直流变压器处于DCM模式,等效工作频率2.5 kHz。将等效工作频率增加至3 kHz,则桥臂电流在正半周期处于DCM模式和CCM模式的边界处,在负半周期中处于在DCM模式,如图11b所示。由于三个子模块电容级联,故桥臂电流在正半周期中以较低频率谐振。进一步将等效工作频率增加到3.5 kHz,则完全处于CCM模式运行,整流器输入电流在每半个运行周期结束时被强制换向,这可以从图11c中观察到。从图11中可看出,正半周期中的桥臂电流波形与负半周期中的桥臂电流波形略有不同,因为用于承受母线电压的子模块数量从3变为5,因此,级联电容总数的变化是不可忽略的。图11(d)中直流变压器处于DCM模式,等效工作频率2 kHz。将等效工作频率增加至2.5 kHz,则桥臂电流在正半周期处于CCM,在负半周期中处于DCM模式,如图11e所示。进一步将等效工作频率增加到3 kHz,则完全处于CCM模式运行,如图11f中所示。

图9 当X=5和Y=4时直流变压器实验波形Fig.9 Test waves of the DC Transformer with X=5 and Y=4
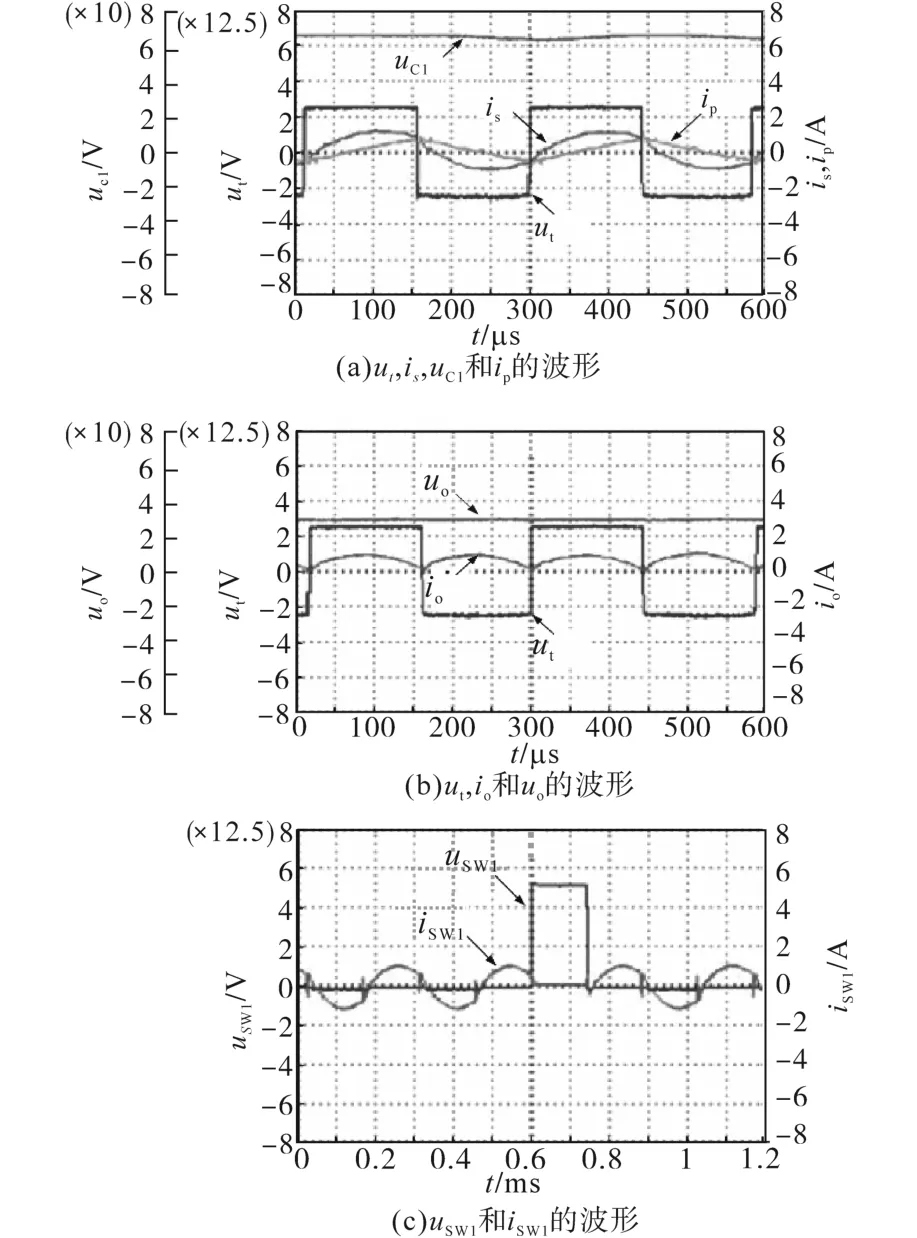
图10 工作频率为3.5 kHz时的直流变压器波形(X=5,Y=4)Fig.10 Experimental waveforms of DC transformer with 3.5 kHz operating frequency(X=5,Y=4)
设置输入电压Udc=300 V和X=5的来测试子模块的固有电容电压自平衡能力,实验结果如图12所示。可以看出,在X=5时,所有调制方案下的子模块电容器电压固有的平衡。
为了实现高压直流电网中不同电压等级的电能变换,设计了一种基于谐振式MMC的直流变压器,同时研究了谐振式MMC在不同调制方案下的工作原理和对应直流变压器变比关系。研究结果表明,使用不同的调制方法,可使谐振MMC实现从(N+1)/(N-1)至2N-1的灵活变比,其中N是子模块数量。选择合适的调制方案后,即在设置X和Y不具有任何公约数时,谐振式MMC具有固有的子模块电容电压自平衡能力。同时,基于谐振式MMC的直流变压器具有良好的线性度和灵活可扩展性。最后,通过实验室的原理样机实验验证了分析和设计。
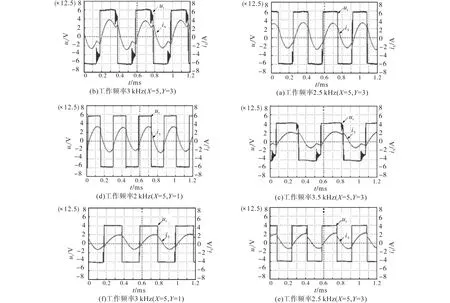
图11 整流器输入电压和桥臂电流实验波形(当X=5和Y=3时和当X=5和Y=1时)Fig.11 Experimental waveforms of rectifier input voltage andarm current with X=5 and Y=3 or X=5 and Y=1
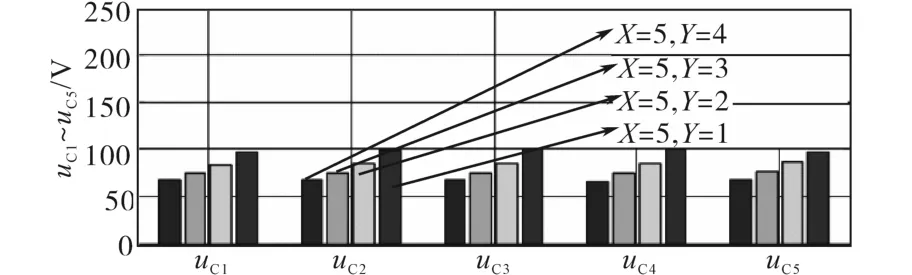
图12 子模块电容电压平衡实验结果Fig.12 Submodule capacitor voltage balance experiment results
