多机系统励磁与UPFC非线性协调控制策略研究

（国网陕西省电力公司电力科学研究院，陕西 西安 710100）

统一潮流控制器（UPFC）是目前柔性交流输电系统（flexible AC transmission system，FACTS）中功能最强大、综合性能最好的装置[1-2]。由于UPFC集合了静止同步补偿器（static synchronous compensator，STATCOM）和静止同步串联补偿器（static synchronous series compensator，SSSC）的优点，在互联电网潮流控制、稳定电压、提高电网稳定性方面均表现出良好的应用效果，因此其控制策略的研究是当前电力系统研究的热点[3]。文献[4]通过将UPFC的有功和无功潮流解耦设计了UPFC并联侧的控制器，并通过三环解耦设计了其串联侧的控制器，但是这种控制方式破坏了UPFC的非线性特性。文献[5]利用暂态能量函数法和模糊滑模控制法设计了UPFC的控制器来抑制系统的低频振荡，但控制器设计基于的模型是系统等效模型。文献[6]通过构造UPFC的Lyapunov函数和坐标变换完成了UPFC控制器设计，但是在控制器设计过程中仍进行了部分线性化处理。由于UPFC装置及电力系统都是非线性系统，因此需要利用非线性方法设计系统的稳定控制器。

Hamilton系统理论上可以根据系统的内部结构特征，在不经过任何线性化处理的基础上完成控制器的设计，因此在非线性系统控制方面具有广阔的应用前景[7]。文献[8]利用广义Hamilton理论设计了TCSC（thyristor controlled series compensator）的控制器并在仿真平台上搭建实际电网模型验证了其控制效果。文献[9]通过无源控制方法设计了电网稳定控制器，并在设计中考虑了相关元件的转移电导。文献[10]在考虑发电机广域励磁信号存在时滞的前提下，通过伪广义Hamilton理论设计了STATCOM与时滞励磁的协调控制器。但是，利用Hamilton系统理论设计UPFC控制器的研究还很欠缺。

本文在考虑系统相关元件转移电导的情况下根据Hamilton系统理论设计了多机励磁和UPFC的协调控制策略。在定义出UPFC对电网影响的前提下，建立了包含UPFC装置的多机电力系统数学模型。进而将此系统表示成含参数扰动的广义Hamilton系统形式。根据边界函数法和L2干扰抑制控制法设计了相应的协调控制器。系统动态响应结果表明了本文所提非线性协调控制策略的正确性和良好应用效果。

1 广义Hamilton理论L2干扰抑制控制法

考虑如下的含有扰动项的仿射非线性系统：

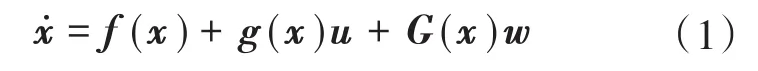
式中：x为系统的n维状态变量，x∈ Rn；f(x)为n维微分流形；u为m维控制输入向量，u∈Rm；w为系统的s维扰动项，w∈ Rs；g(x)，G(x)为适当阶数的系数矩阵。

若存在一个标量函数H(x)，则能将式（1）所示的系统表示为

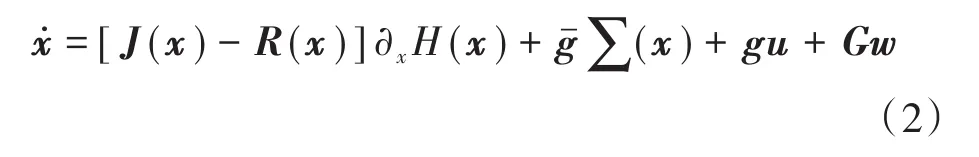
式（2）中的∑(x)在x的定义域上是一致有界的，并且在系统的平衡点x0处的取值为零，此式中其余变量的含义可以参考文献[11]。根据边界函数理论[12]，∑(x)的表达式需要满足下式：

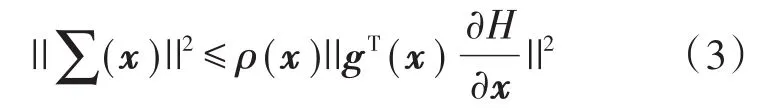
式中：ρ(x)是一个正定函数。

由于系统中含有参数扰动，则考虑如下的惩罚函数：

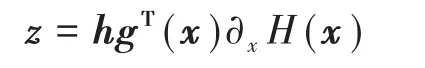
式中：h为权重矩阵。

当式（2）所示系统满足以下三点要求时：

1）式（2）所示系统是零状态可检的；

2）系统的Hamilton函数H(x)为非负定函数；

3）给定的干扰抑制水平γ（大于零）满足：

则可令控制变量u满足下式，从而使系统在平衡点x0处渐近稳定：

式中：λ为满足R(x)-λ/2gˉgˉT≥ 0的非负数；I为单位对角矩阵。

上述控制策略的推导过程详见文献[13]。

2 含UPFC装置的多机电力系统广义Hamilton系统实现

本文所研究的n机系统包含m个负荷节点和一台UPFC装置。其中发电机采用三阶模型，1,2,…,n为其节点；n+1和n+2为安装有UPFC的母线节点；n+3,…,n+m+2为负荷节点。

2.1 UPFC的动态模型

UPFC装置可以看成是由一台STATCOM和一台SSSC合并而成的，其模型结构图如图1所示。

UPFC的非线性动态方程[14]如下：

式中，id1，iq1分别为UPFC并联部分注入的d轴和q轴电流；id2，iq2分别为UPFC串联部分注入的d轴和q轴电流；Un+1∠θn+1，Un+2∠θn+2分别为UPFC并联部分和串联部分接入母线的电压；Rs1，Ls1分别为并联耦合变压器的等效电阻和漏电感；Rs2，Ls2分别为串联耦合变压器的等效电阻和漏电感；Cdc为直流侧电容器的电容；Rdc为两个换流器的等效切换损失；Udc为直流侧电容电压；ωs为系统角频率；ζ1,ζ2,ζ3,ζ4为UPFC的等效有界输入扰动；k1，k2分别为并联侧换流器调制比和串联侧换流器调制比；α1，α2分别为并联侧换流器相位移和串联侧换流器相位移；其中的ωs为有名值，其余变量均为标幺值。

定义UPFC的控制输入变量为u1，u2，u3和u4，其表达式为

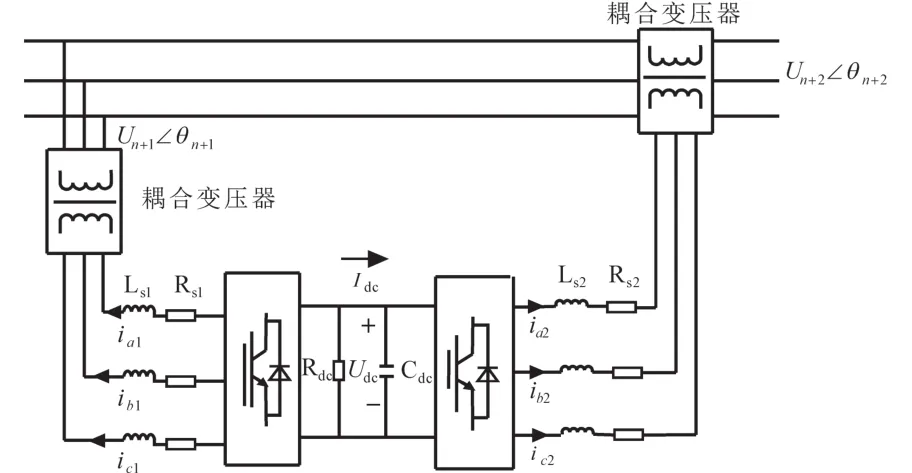
图1 UPFC的电路结构图Fig.1 Circuit structure diagram of UPFC

2.2 多机电力系统模型

将由于UPFC装置的存在，电力系统中发电机输出的附加电磁功率和d轴电流定义为ΔPei和ΔIdi。则在n机电力系统中第i台发电机的三阶动态方程为

式中：下标i为第i台发电机的相应变量，i=1,2,…,n；ωi为发电机角速度；ω0为是发电机同步角速度；xdi为发电机的d轴同步电抗；x′di为发电机的d轴暂态电抗；T′d0i为发电机的d轴暂态开路时间常数；E′qi为发电机的q轴暂态电势；Gij，Bij分别为发电机i与发电机j间的互电导及互电纳；δij为E′qi的复矢量与E′qj的复矢量之间的相角差；Di，Mi分别发电机的阻尼系数和惯性时间常数；Pmi为固定的机械输入功率；ufi为发电机励磁输入控制量；Efis为平衡状态下励磁电压值；wi1，wi2为发电机的有界输入扰动。

2.3 系统的广义Hamilton形式实现

在得到UPFC装置和第i台发电机的数学模型后，联立式（5）和式（7）就可以得到含有UPFC装置的多机电力系统的数学模型表达式。根据实际电力系统将x=[δ1,ω1,E′q1,…,δn,ωn,E′qn,id1,iq1,id2,iq2,Udc]T作为其状态变量，系统的初始平衡点为x0。为了简便，后续表述定义：

构造上述系统的Hamilton能量函数为

此能量函数H(x)具有明确的物理意义，代表了包含UPFC装置附加能量在内的系统总能量。

计算能量函数H(x)对各个状态变量的偏导数，则多机系统的动态方程可表示为

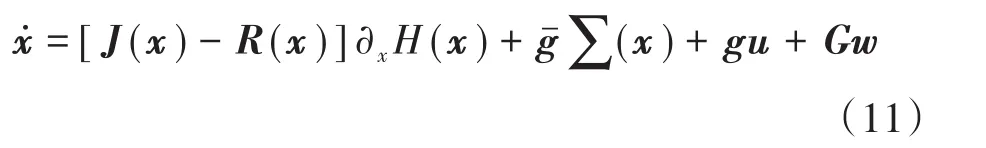
式中：u为多机电力系统的控制输入量；u10，u20，u30，u40分别为UPFC在系统平衡状态下的控制变量初始值；id10，iq10，id20，iq20为UPFC在系统平衡状态下的初始值；w为多维扰动矩阵。

3 发电机励磁与UPFC装置的协调控制器设计

将装设有UPFC的多机电力系统表示成广义Hamilton形式后，要想利用式（4）所示的扩展L2干扰抑制控制法设计系统的协调控制器，需要首先验证一下系统的几个性质：

1）当控制变量u=0时，很明显多机系统是零状态可检的。

2）从H(x)的表达式可以看出，在x0处，H(x)的值为零，并且∂xH(x)|x=x0=0。要想保证H(x)为非负定函数，就要求其Hessian矩阵正定。但是像H(x)这样一个复杂函数的Hessian矩阵的正定条件很难用具体表达式给出，故通常采用计算机数值计算法进行判定[15]。

3）通过对下式进行计算来确定系统的干扰抑制水平γ：

并且从∑(x)的表达式可以验证∑(x0)=0且在x的定义域空间中一致有界。根据式（3）可定义出ρ(x)=[ρ1i(x),ρ2(x)]T，只要找到合适的ρ(x)就可以根据式（4）来设计多机励磁与UPFC装置的非线性协调控制策略。

多机系统中第i台发电机励磁的控制策略为

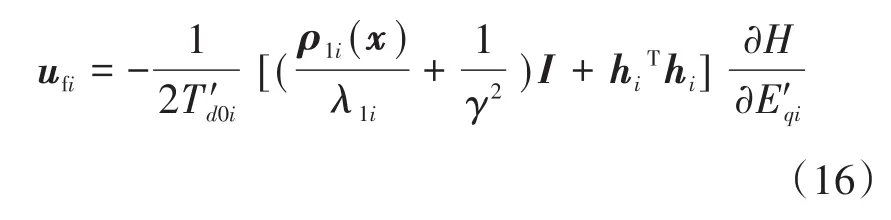
式中：hi为特定系数。

UPFC装置的控制策略为

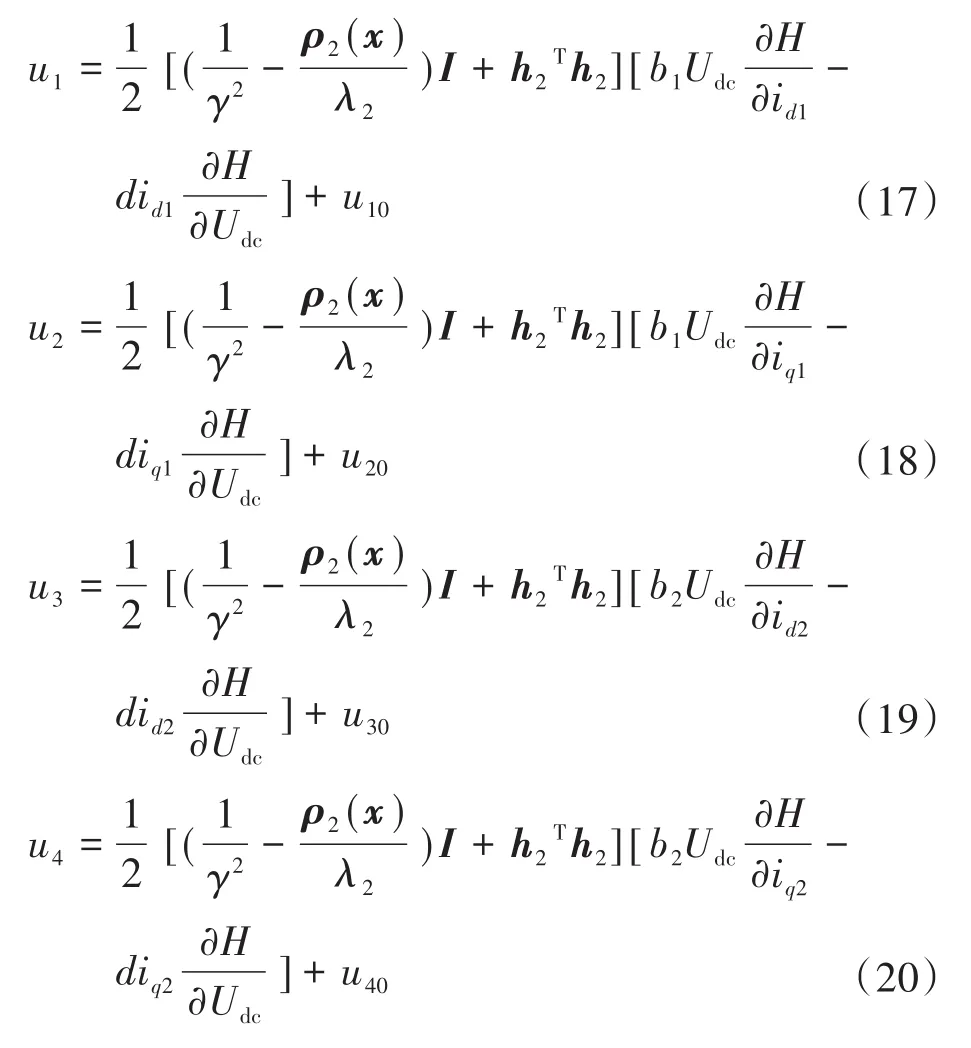
式中：h2为待定系数。

由式（6）可将u10，u20，u30，u40转化成UPFC装置的触发控制变量：

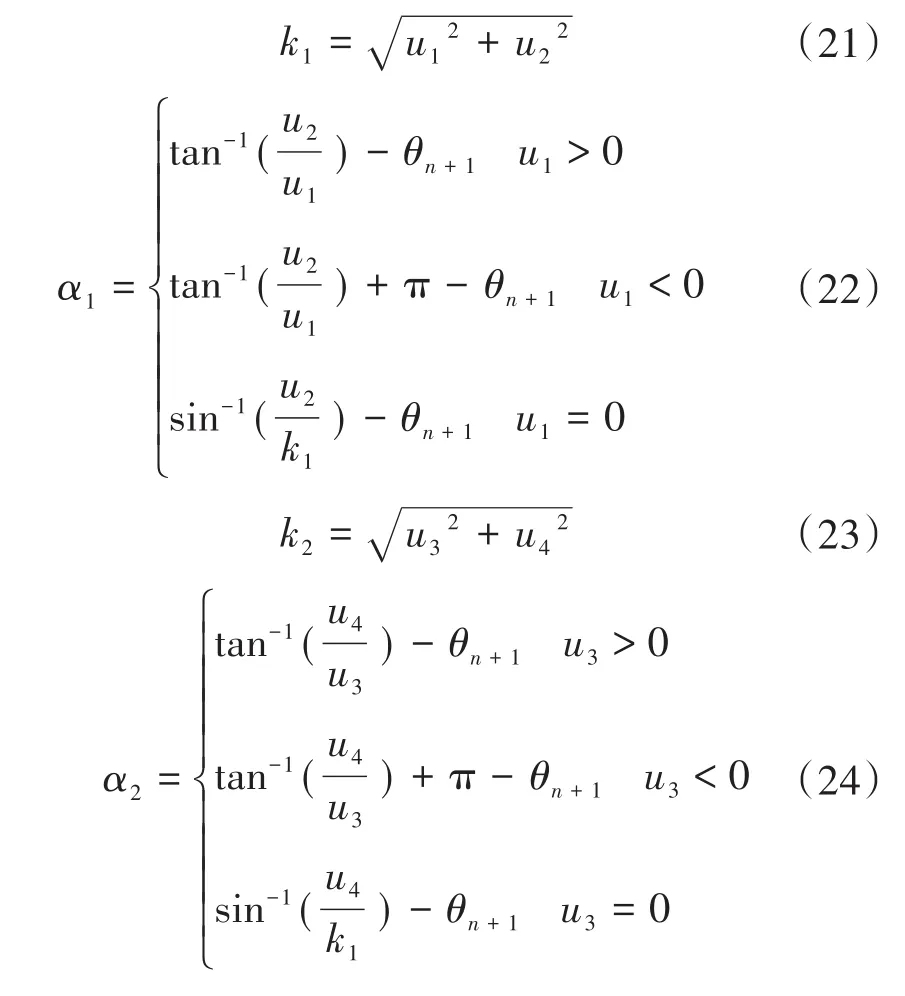
4 仿真分析与验证

为验证本文所提的多机励磁与UPFC的协调控制策略的有效性，在PSCAD仿真环境中搭建如图2所示的包含UPFC装置的四机两区域仿真模型。此仿真模型中所有发电机的额定容量为900 MV·A，额定电压是20 kV。系统输出电压的额定值为230 kV。以额定值为基准值的发电机和UPFC装置的具体仿真参数分别如表1和表2所示。根据系统在平衡点处的初始值和第1节所述控制理论的约束条件通过多次仿真优化法确定控制器参数，取λ1i=λ2=0.1，hi=h2=2，γ=2，边界函数取通过PSCAD/EMTDC仿真平台中测量单元的测量值来模拟实际系统中PMU装置的测量值，为本仿真提供所需的发电机和UPFC装置的实时运行参数。

图2 四机两区域系统结构图Fig.2 The system structure of two-area including four generators

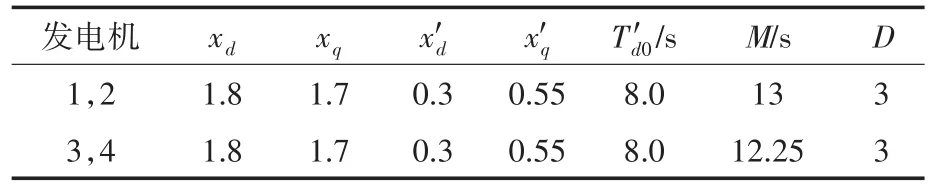
表1 发电机仿真参数Tab.1 Generator simulation parameters

表2 UPFC装置仿真参数Tab.2 UPFC device simulation parameters

本仿真中系统初始运行于稳定平衡点，设定的系统故障情况如下：1）UPFC装置串联母线右侧在2 s时发生三相瞬时性接地短路故障，0.1 s后故障切除，系统恢复正常；2）母线7处的负荷在2 s时忽然减少为原来的50%，并在2.5 s时恢复正常负荷。为了充分验证本文所提非线性控制策略的有效性，将其与由发电机的AVR/PSS和UPFC的PI控制组成的分散控制进行对比仿真。

故障1的设定用来验证非线性协调控制器的有效性；故障2的设定用来验证非线性协调控制器的鲁棒性。图3～图8分别展示了系统联络线传输功率、发电机功角差及母线9电压在两种故障情况下的动态响应曲线。

图3 G1和G3的功角差Δδ13的响应曲线（故障1）Fig.3 Response curves of the power angle difference Δδ13betweenG1andG3（fault 1）

图4 联络线传输功率P7-8的响应曲线（故障1）Fig.4 Response curves of tie line transmission powerP7-8（fault 1）

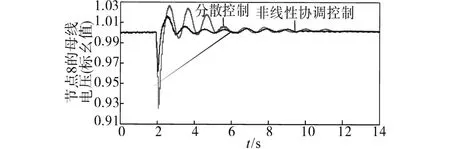
图5 母线9电压的响应曲线（故障1）Fig.5 Response curves of bus 9 voltage（fault 1）

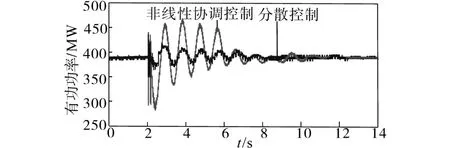
图6 G1和G3的功角差Δδ13的响应曲线（故障2）Fig.6 Response curves of the power angle difference Δδ13betweenG1andG3（fault 2）

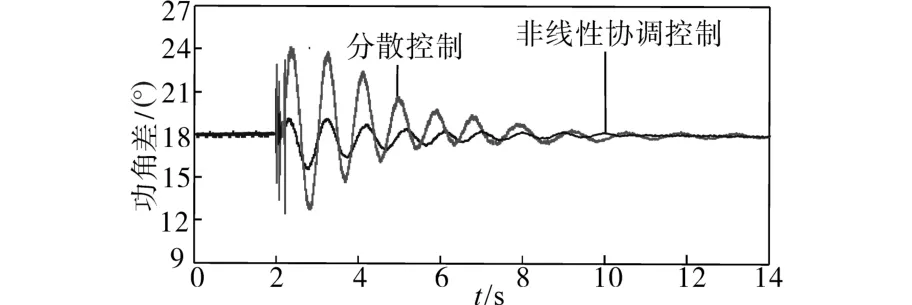
图7 联络线传输功率P7-8的响应曲线（故障2）Fig.7 Response curves of tie line transmission powerP7-8（fault 2）

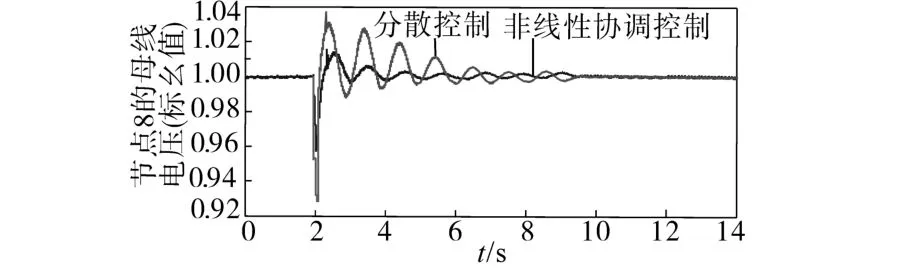
图8 母线9电压的响应曲线（故障2）Fig.8 Response curves of bus 9 voltage（fault 2）

从图3～图8中可以看出，与传统分散控制相比，本文设计的非线性协调控制器具有较快的响应速度，并且能够以较小的超调量在较短的时间内使系统迅速恢复稳定，从而验证了本控制器的有效性和鲁棒性。

5 结论

本文利用广义Hamilton理论的扩展L2干扰抑制控制法设计了多台发电机励磁与UPFC装置的协调控制器，解决了具有参数扰动的含UPFC装置的多机电力系统的稳定性问题，同时系统动态方程的建立和Hamilton函数的构造为研究多台UPFC装置和多台发电机的协调控制问题提供了基础。仿真结果验证了所提非线性控制器的有效性和鲁棒性。本文中的一些控制器参数是通过多次仿真优化得到的。下一步工作的重点是，研究一种适用于确定非线性控制器参数的简便优化方法。