利用多基数系统的高效椭圆曲线多标量乘算法

尤文珠，葛海波

（西安邮电大学电子工程学院，西安 710121）

0 概述

随着无线通信技术的快速发展，人们对物联网安全的需求与日俱增，而加密技术可在确保用户身份验证和授权、通信数据机密性和完整性等方面发挥重要作用。自1975年RIVEST、SHAMIR和ADLEMAN提出RSA公钥密码体制以来，其得到了广泛的研究和应用，但该系统严重依赖使用1 024 bit和2 048 bit等大密钥位的整数分解难题（Integer Factorization Problem，IFP）［1］。之后，MILLER［2］和KOBLITZ［3］提出的椭圆曲线密码体制（Elliptic Curve Cryptography，ECC）使该情况得到了改善。ECC具有与RSA相同功能的公钥密码体制［4］，其计算原理是求解椭圆曲线离散对数问题（Ellipse Curve Discrete Logarithm Problem，ECDLP）。相比当前主流的加密系统，ECC以更小的密钥尺寸提供了更高级别的安全性，并且运行速度快，适用于计算资源受限的智能移动终端。

ECC中的标量乘法相比其他运算层是求逆次数最多且最核心的运算，标量乘法的运算速率对实现整个密码体制的性能起到关键作用。标量乘运算又称为点乘运算，即其中，k是一个整数，P为椭圆曲线上的一个基点。在多数情况下，二元表示、非邻接形式（Non-Adjacent Form，NAF）、滑动窗口法以及双基多基标量乘等［5-6］方法通过研究标量k来改进标量乘运算，从而找到更有效表示k的方法。ECC中的多标量乘运算在ECDH［7］等密码协商协议中具有重要作用，可表示为k1P1+k2P2+…+km Pm，在验证椭圆曲线数字签名时通常需要计算kP+JQ［8］，其中，P、Q是椭圆曲线上的两个基点，k、J是两个正整数。ECC中的直接算法、Shamir算法［9］、交错NAF算法［10］等多标量乘算法都是通过将ki分解为0和1比特串使其最大限度地出现零列。

文献［11］提出双基数系统（Double-Base Number System，DBNS）。文献［12］改进双基思想，将其扩展为多基数系统（Multi-Base Number System，MBNS），且提出5倍点的计算公式及标量乘法，大幅提高了计算速度。文献［13］主要给出一种k1，k2，…，km的带符号二进制表示方法，使其全零列的数量尽可能多，并且在此基础上提出一种新的计算多标量乘的算法，降低了算法时间复杂度。文献［14］提出一种基于互反形式（MOF）的标量乘并行计算方法。文献［15］从计算复杂度的角度研究ECC标准曲线优化问题，提出一种基于w-NAF（其中w表示窗口宽度）的标量点乘算法。文献［16］研究基于NAF的ECC标量乘算法优化问题，提出一种将加减标量乘算法与NAF表示相结合的新算法，提高了ECC计算性能。文献［17］将双基数系统用于多点乘运算并提出3种基于双基数系统的多点乘算法。本文在文献［17］算法的基础上，提出一种以2、3、7为基元的多基链整数表示方法和两种多标量乘快速算法。

1 相关概念

1.1 椭圆曲线定义

定义1有限域上的椭圆曲线方程在域K上定义为［11］：

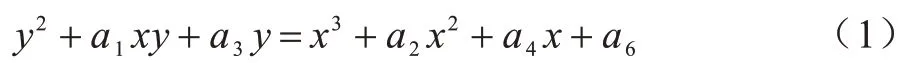
其中，系数a1，a2，a3，a4，a6∈K，Δ≠0，Δ为椭圆曲线判别式，域K中的每个点(x1，y1)都满足式（1）。在素域K=Fp上，式（1）可简化为：

其中，a，b∈K，Δ=4a3+27b2。

在二元域K=F2上，式（1）可简化为：

其中，a，b∈K，Δ=b≠0。

标量乘运算在实现过程中会调用点加和倍点运算，而点加和倍点运算又会再调用底层有限域算术运算，即标量乘算法的运算效率受底层域运算的影响。表1给出了有限域中相关操作的运算量统计，其中，I表示求逆操作，S和M表示平方和乘法操作。

表1 相关操作的运算量统计Table 1 Statistics of computation amount of related operations

1.2 整数k 的双基表示

双基链是椭圆曲线标量乘算法的一种加速方法，其中每个正整数n都可表示为2a3b的和或差形式。

定义2设集合B={2，3}，则整数k可表示为如下形式［1］：

该形式为整数k的双基链表示，其中，{ai}，{bi} 为单调递减序列，di∈{-1，1}。双基链表示高度稀疏，可减少标量展开的汉明权值。由于三元基表示方法引入了高效的三倍公式，因此其大幅减少了标量乘法的运行时间。例如，使用双基链计算4012174=21137-2936-2835-2735+2532+2431-2130。

1.3 w-NAF算法

整数k可表示为长度为l的二进制序列，考虑到NAF一次只能处理两个连续的相邻位。w-NAF对NAF进行了扩充［18］，采用整数k的w位表示，这样便可使非零元素的取值范围从[-1，1 ]扩展到[-2w-1，2w-1-1]。令w≥2，则正整数k的w位宽度的NAF表达式为：

其中，ki是奇数且|kj|＜2w-1。

算法1w-NAF算法

2 多基整数表示方法和多标量乘算法

2.1 多基整数表示方法

多基数系统作为双基数系统的一个扩展，其汉明重量变小，标量表示链长也随之变短，进而使标量乘运算效率得到明显提高。对于一组小整数集合B={b1，b2，…，bi}，如果用元素和的形式来表示标量k，则任何一个整数k都可以表示为其中si表示符号位，{ei1}，{ei2}，…，{eil}≥0为单调递减序列。由于多基整数表示系统将{2，3，7}作为多基系统的基元，因此本文提出标量k的多基表示方法。

定义3设集合B={2，3，7}，则整数k可以表示成如下形式：

该形式即为整数的多基数表示，其中，{bi}、{ti}、{qi}变化呈递减形式，si∈{-1，1}，m为多基数表示的长度。多基链相较双基链冗余度不仅更高，而且汉明重量也更小。例如，当si=1时，整数100总计有402个双基数表示方法，而多基数表示可达8 425个［19］。bi、ti、qi的数值大小对2、3、7倍点运算的运算次数有直接影响。使用DBNS表示一个160位的大数，需约23项，然而使用MBNS表示则仅需约15项［20］。由此可看出，使用多基链能有效提高ECC中的标量乘法运行效率，通常采用贪婪算法编码可获得多基链的整数表示。

算法2贪婪算法

2.2 基于MBNS滑动窗口的多标量乘快速算法

算法3采用滑动窗口算法可以有效降低时间复杂度。该算法运行在底层元素集合的大数组上的一个子列表上，在运行整个列表时会进行特定操作，动态寻找窗口以减少存储空间，其中实际窗口计算数小于d。点加的运算次数由多基表示的链长和非零位数决定，也会随着窗口宽度w的变化而变化。基于算法3的有限域中窗口宽度及相应点加平均运算次数如表2所示，其中表示二元域，E(FP)表示素域分别表示二元域和素域上不同窗口宽度下的平均点加次数。

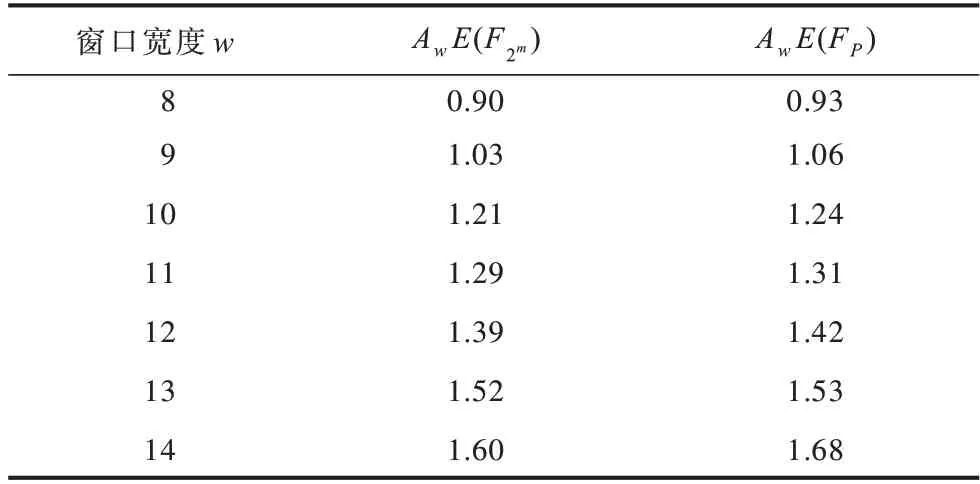
表2 基于算法3的有限域窗口宽度及相应点加平均运算次数Table 2 The window widths and the average computation number of corresponding point plus in the finite field based on algorithm 3

算法3中假设基点已知，即定点标量乘运算，因此无需多次更换预计算表，主要计算赋值阶段的运算消耗。本文在jmax=3下对算法性能进行分析研究，先对MBNS表示的每个窗口进行点加操作，然后分别对i(i=3)个标量求和，算法3在赋值阶段所需总的点加运算次数为

2.3 基于交错MBNS滑动窗口的多标量乘快速算法

基于交错MBNS滑动窗口的多标量乘快速算法I-MB NS采用w-NAF表示，只需计算小于2w-1的奇数项。例如，对于一个数的7-NAF表示，只需计算介于-63～63的奇数项，因此其点加运算次数会减少。首先计算标量kj的NAFw形式，其次进行预处理操作，使用MBNS表示串并计算出iP1、mP2、的数值结果，最后根据预处理值，经点加和倍点的反复运算操作得到

算法4基于交错MBNS滑动窗口的多标量乘快速算法

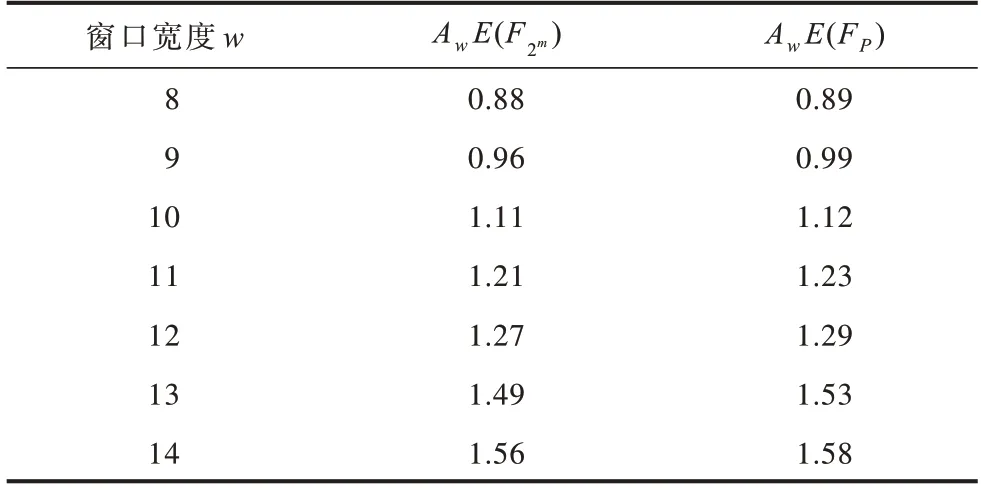
表3 基于算法4的有限域窗口宽度及相应点加平均运算次数Table 3 The window widths and the average computation number of corresponding point plus in the finite field based on algorithm 4

3 运算效率分析

本文对Sliding MBNS和I-MBNS算法在jmax=3下进行实验并用Python实现上述算法。为便于算法性能对比，Shamir算法［21］和交错NAF算法［22］的窗口大小分别为2 bit和4 bit～8 bit，Sliding MBNS和I-MBNS算法的窗口大小为10 bit～16 bit。表4将Shamir算法、交错NAF算法、Sliding MBNS和I-MBNS算法在二元域（E(F2m)）和素域（E(FP)）上的底层域平均运算量进行比较，设置，标量长度分别取160 bit、192 bit和230 bit。

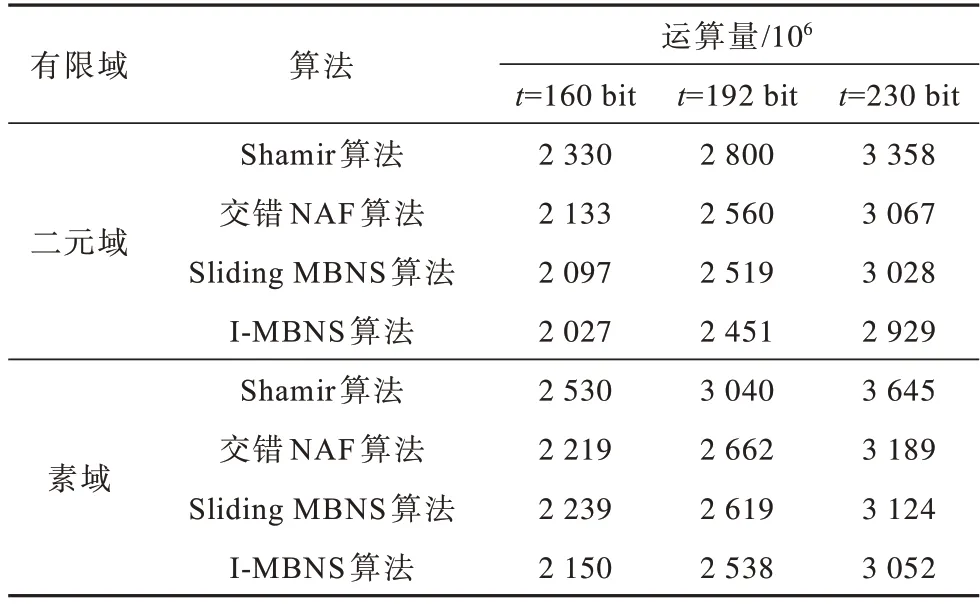
表4 算法平均运算量比较Table 4 Comparison of average computation amount of algorithms

根据实验数据分析可知：在二元域上t=160 bit时，Sliding MBNS算法相比Shamir算法和交错NAF算法运算量分别减少了10.00%和1.69%；I-MBNS算法相比Shamir算法和交错NAF算法运算量分别减少了13.00% 和4.97%。在素域上t=160 bit时，Sliding MBNS算法相比Shamir算法运算量减少了11.50%，I-MBNS算法相比Shamir算法和交错NAF算法运算量分别减少了15.02%和3.11%。Shamir、交错NAF、Sliding MBNS和I-MBNS算法在二元域和素域上的运算量对比结果如图1和图2所示。由图1和图2可以看出，无论二元域还是素数域，Sliding MBNS和I-MBNS算法的运算量明显低于Shamir和交错NAF算法，运算效率更高。本文还分析了算法运算量与窗口宽度的关系。以二元域I-MBNS为例，t=160 bit时不同窗口对应的平均运算量如表5所示。

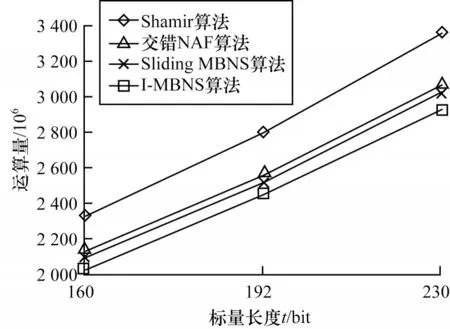
图1 二元域算法运算量对比结果Fig.1 Comparison results of algorithm computation amount in binary domain

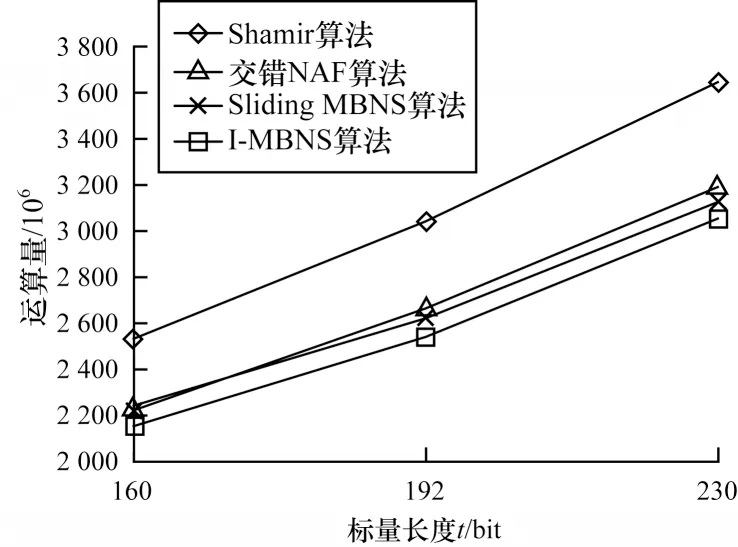
图2 素域算法运算量对比结果Fig.2 Comparison result of algorithm computatuion amount in prime field

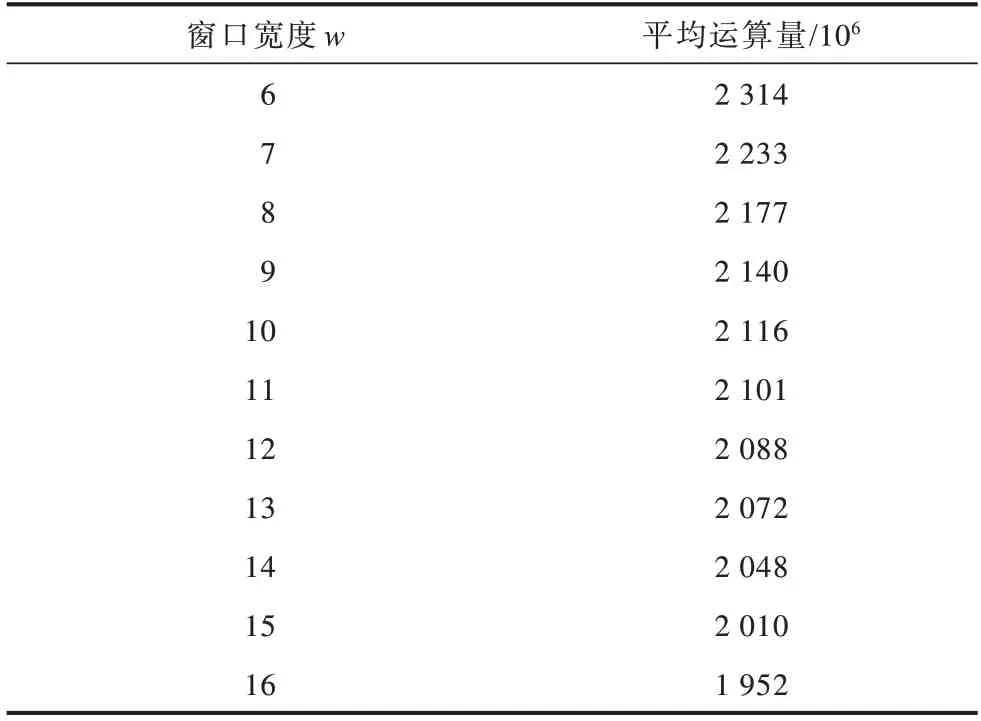
表5 t=160 bit时不同窗口宽度对应的平均运算量Table 5 Average computation amount corresponding to different window widths when t=160 bit

由表5可知，不同窗口宽度对应的平均运算量不同，并且随着窗口宽度的不断增大，平均运算量逐渐减少。为能更清晰地显示两者之间的变化情况，绘制二元域窗口宽度与平均运算量的曲线图，如图3所示。可以看出，当t=160 bit时，随着I-MBNS算法窗口宽度的不断增大，平均运算量呈下降趋势。

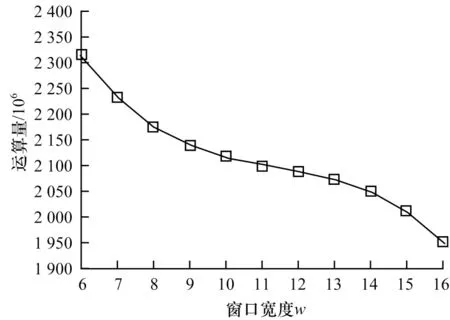
图3 二元域窗口宽度与平均运算量的关系Fig.3 The relationship between the window widths and the average computation amount in binary domain

4 结束语

本文结合多基数系统和滑动窗口算法，提出一种以2、3、7为基元的多基整数表示形式及Sliding MBNS和I-MBNS两种多标量乘算法，分析并比较了Sliding MBNS和I-MBNS算法在二元域和素域及不同窗口宽度下的平均运算量。实验结果表明，Sliding MBNS和I-MBNS算法大幅提升了运算效率，且随着窗口宽度的不断增加，平均运算量呈现下降趋势，进而加速多标量乘运算及ECC整体实现。下一步将融合目前主流椭圆曲线密码体制的硬件实现，将标量乘算法应用于网络信息安全传输中，保证信息传输的高效性和安全性。