基于交叠组稀疏非凸Lp伪范数高阶全变分的地震随机噪声压制

2021-02-05梁上林胡天跃隋京坤

石油地球物理勘探 2021年1期

梁上林胡天跃* 崔栋隋京坤

(①北京大学地球与空间科学学院，北京 100871； ②中国石油勘探开发研究院，北京 100083)

0 引言

地震记录中常常混杂着大量的随机噪声，严重降低了资料的信噪比。有效压制地震数据中的随机噪声是地震资料处理的重要环节。然而，由于其产生具有随机性且无固定频率和视速度，随机噪声压制一直是勘探地球物理界的难点之一。目前，压制随机噪声的方法可归纳为时间域滤波[1-2]、频率域滤波[3]、空间域滤波[4]和各种变换域滤波[5-9]等。Rudin等[4]于1992年首次提出空间域的全变分(Total variation，TV)模型，利用含噪数据总变分比无噪信号总变分大的性质，构造能量泛函以达到去噪的目的。鉴于其有效性，该模型被广泛应用于噪声压制[10-12]、波阻抗反演[13]和全波形反演[14]等领域。

尽管TV模型具有保护图像边缘信息的优势，但存在严重的阶梯效应，导致信号分片光滑。针对此问题，Selesnick等[15]率先将交叠组稀疏(Overlapping group sparsity，OGS)引入TV模型，指出信号的一阶差分不仅具有稀疏特性，还具有结构稀疏特性。之后Selesnick等[16]通过正则化技术有效识别出平滑区域内被强噪声污染的信号。为挖掘图像一阶梯度和二阶梯度的结构稀疏性，陈颖频等[17]将OGS与TV模型相结合，构建了一种改进的去噪模型。

上述方法[15-17]从本质上都是在寻找不同的正则项及惩罚函数，以达到最佳去噪效果。考虑到L1正则项是一种凸近似，往往使重构的非零信号比真实值小而导致过拟合，Ahlad等[18]提出组内使用L2范数和组间使用L1范数的加权方式。Lp伪范数本质是一种非凸正则项，它具有比凸核更接近秩函数的优点，能在恢复信号细节与给定残差稀疏解之间达到平衡，被广泛应用于图形修复、地震数据重建和重力反演等领域[19-21]。Adam等[22-23]基于高阶TV模型，引入非凸正则项技术，在图形去模糊方面取得一定效果；同时指出OGS与非凸高阶TV模型在去除斑块虚假信息上是互补的。然而，目前尚未见到将Lp伪范数、OGS和TV模型三者相结合应用于地震资料去噪的实例。

鉴于一阶TV模型不能有效保护信号的边缘及纹理特征，存在严重的阶梯效应，本文将高阶TV模型与OGS相结合，目的是充分挖掘和利用两者的优点，在减弱阶梯效应的同时较好地保护局部信息；同时，为解决信号重构过程中产生的斑点和块状问题，保护非零有效信号，引入非凸Lp伪范数；最后通过模拟数据和实际资料对本文方法进行验证，并与常规五种去噪方法进行对比。

1 去噪原理

1.1 传统TV去噪模型

实际地震数据可表示为

y=s+n

(1)

式中：y表示检波器接收到的地震数据；s表示有效信号；n为随机噪声。TV去噪模型对应如下数学极值问题[4]

(2)

1.2 二维OGS正则项

Selesnick等[15]定义了窗尺度为K×K且中心点为(i,j)的二维矩阵

(3)

m1=K-12、m2=K2,

式中表示向下取整，K表示组稀疏交叠程度。二维OGS正则项定义为

(4)

可见，OGS将邻域信息作为参考形成组合梯度，能充分挖掘信号的局部相似性。

1.3 基于OGS非凸Lp伪范数高阶TV模型

考虑到OGS能有效恢复全局较大轮廓而高阶TV模型可较好地保护局部弱信号，将OGS与高阶TV模型结合，充分利用两者优点形成一个混合去噪模型；同时，引入非凸Lp伪范数以更准确地重构噪声数据中非零信号。该模型所对应的数学极值问题[22]表示为

(5)

改进的方法是以信号周围点的信息作为参考形成组合梯度，使孤立的噪声污染点与邻域的组合梯度下降；同时保持图像边缘点与邻域的组合梯度强度，通过设定合理的阈值，可在有效去除噪声的同时，减弱阶梯效应，较好地保护有效信号。

采用分离变量法将式(5)转化成如下受约束的极值问题

s.t.a=s,b=2s,c=s

(6)

该式对应的无约束增广拉格朗日极值为

L(s,a,b,c;ξ1,ξ2,ξ3)=

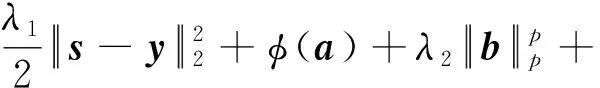
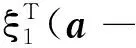
(7)

为求解式(7)所示的复杂耦合问题，本文采用交替方向乘子法(Alternating direction method of multipliers，ADMM)[25]，按照下式交替迭代更新

(8)

可见，式(7)所示耦合问题被分解成四个子问题。下面利用式(9)～式(13)求解相应子问题。

sk+1是一个最小平方问题，其解析解为

sk+1=[λ1I+βT+β(2)T2+βI]-1[λ1y-Tξ1+

βTak-(2)Tξ2+β(2)Tbk-ξ3+βck]

(9)

ak+1的约束如下

(10)

式中包含了式(4)所示的OGS正则项，当K=1时式(10)退化成传统的高阶TV模型；当K>1时，式(10)表示求解OGS正则项。鉴于最大最小值(Majorization minimization，MM)算法具有高效利用函数凹凸性搜寻原函数最值的优点，当原目标函数难优化时，不直接对其求解，而是求解一个易于优化且逼近于原目标函数的替代函数[26]。本文通过二次函数替代φ(a)实现MM算法。

同理，bk+1的约束为

(11)

式(11)是一个非凸优化问题。非凸优化算法和阈值的选取是决定去噪效果的两个重要因素。鉴于经典的加权方向迭代L1算法能有效平衡信号的正负二阶微分[27-28]，因此本文采用该算法求解

(12)

式中：ζ和ε都是较小量，用以避免分母为零； max表示求二者较大值； sign为符号函数。

类似地，ck+1的约束为

(13)

另外，求解式(7)所需的三个拉格朗日乘子可表示如下

(14)

至此，四个子问题已求解完成。

将整个算法流程总结如下：

(1)输入二维地震数据y，给定参数λ1>0，λ2>0，K，p；

(2)初始化模型：s0=y，k=0，β=0.004，si=1,2,3=0，模型更新率εmin=1×10-6；

(3)更新式(9)中的sk+1；

(4)采用MM迭代算法更新式(10)中的ak+1；

(5)更新式(12)中的bk+1；

(6)更新式(13)中的ck+1；

2 模拟数据验证

2.1 评价指标

信噪比通常用信号总能量与噪声总能量的比值SNR(Signal to noise ratio)表征，是评价整体去噪效果的常用指标；结构相似性参数SSIM(Structural similarity)从亮度、对比度、结构三方面度量两幅图像的相似性，常作为衡量图像失真或噪声压制情况的客观标准[29]；同时，为表征高斯噪声强弱，定义零均值噪声的标准差为δ。三者的具体定义如下

(15)

(16)

(17)

式中：M、N分别表示二维地震数据的行数和列数；μs、μy对应表示s、y的均值；σs、σy分别表示s、y的方差；σsy表示s与y的协方差；C1和C2是维持稳定的两个常量，一般分别取2.252和6.752。为了更全面地评判去噪效果，本文将SNR、SSIM和运算耗时作为三个客观评价指标。

2.2 模拟数据

构建一个水平层状模型，通过有限差分声波正演模拟得到图1所示的共炮记录。模拟采用主频为20Hz的雷克子波，采样间隔为4ms，采样长度为4s，接收道数为500。为了模拟地震数据中不同强度的随机噪声，向该记录加入标准差为δ的高斯白噪声，得到图2所示的含噪数据。由图2可知，随着δ增大，背景噪声加强，SNR降低，SSIM变差，弱反射信号逐渐被强噪声淹没。

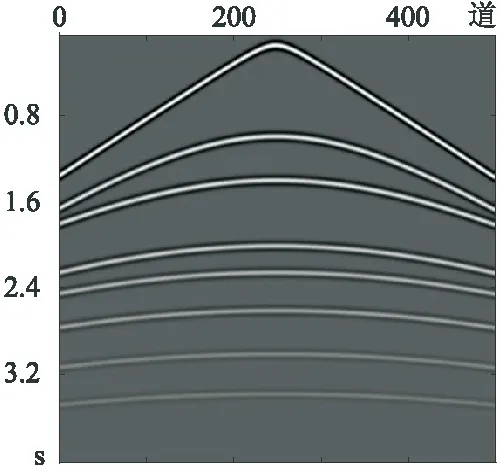
图1 正演模拟共炮记录

图2 不同δ的含噪数据(a)δ=10； (b)δ=20； (c)δ=30； (d)δ=40

2.3 参数优选

OGS从一个点向四周延伸K×K个点，可有效挖掘信号的局部相似性。为考察K值对去噪效果的影响，通过不断调整其大小，分别对图2所示的四种不同噪声背景下的地震数据做去噪处理。

图3展示不同K值得到的去噪结果所对应的三种指标的变化曲线。从图3a可见，随着K值的增大，SNR先从小到大逐渐增加，达到最大值后减小。当SNR取最大值时，K值分别为3、5、7和10，说明K值的优选与背景噪声强度有关。当背景噪声较弱时，较小K值就能达到满意的去噪效果；当背景噪声增强时，应适当增大K值以提高SNR。图3b中的SSIM表现出与SNR类似形态，区别在于当SSIM达到最大值后缓慢减小。这说明K值超过最优值后，对SSIM的影响不显著。图3c显示，随着K值的增大运算耗时也不断增加，这是由于邻域信息的引入，导致计算量增大。

图3 去噪结果的三指标随K值的变化曲线(a)SNR； (b)SSIM； (c)耗时

因此，K值对本文方法去噪效果有显著影响。当K值过小时，邻域信息不足导致SNR和SSIM达不到最优，去噪效果欠佳；而当K值过大时，又会引入过多不相似的数据点，反而导致评价指标减小，去噪能力下降，这不仅会产生平滑效应，还会因使用过多邻域信息增加不必要的计算量。

边界与局部细节的恢复主要受非凸正则化阶数p控制，对图2含噪数据进行处理并得到图4所示三种指标随p的变化曲线。图4a表明，当δ=10时，SNR随p值增大而快速增至最大值，然后快速减小；当δ=20、30和40时，SNR曲线都具有平缓段、快速上升段和快速下降段。在平缓段SNR对p值不敏感，经快速上升后达到最大值。SNR取最大值时对应p值分别为0.23、0.46、0.62和0.75，这说明p值的优选与噪声强度有关。图4b表明，弱噪声情况下SSIM曲线先上升，然后保持平缓；当背景噪声变强时，SSIM曲线呈现平缓段—快速上升段—平缓段分布。该指标取最大值时对应p值分别为0.16、0.47、0.62和0.83。图4c表明，随着p值增大，运算耗时先增至最大值，然后逐渐减小，显然该指标与背景噪声强度无关。

图4 去噪结果的三种指标随p值的变化曲线(a)SNR； (b)SSIM； (c)耗时

综上，p值对本文去噪方法有同样显著的影响。高SNR资料应取较小p值；反之，低SNR资料应适当增大p值，以达到最佳去噪效果。

图5展示K与p最优情形下对图2所示四种不同强度噪声背景下地震数据的去噪效果。不同强度随机噪声均得到有效压制，剖面整体干净，反射波同相轴清晰，深层弱能量信号得到有效保护。

图5 含有不同δ背景噪声数据的去噪结果(a)δ=10； (b)δ=20； (c)δ=30； (d)δ=40

以上去噪试验表明，本文方法能压制阶梯效应，去除不同强度随机噪声，提高信噪比，并能有效保护弱能量信号。

2.4 方法对比

为进一步验证本文方法的有效性，分别与各向异性全变分(Anisotropic total variation，ATV)、交叠组稀疏全变分(Overlapping group sparsity total variation，OGSTV)、中值滤波(Median filter，MF)、三维块匹配(Block matching 3D，BM3D)和K奇异值分解(K-singular value decomposition，KSVD)等五种方法进行对比。其中，ATV和OGSTV与本文方法属于同类，后三者为常用去噪方法。

表1展示这些方法去噪后各项指标对比结果。从SNR和SSIM指标看，本文方法明显优于其他五种方法。从运算耗时指标看，本文方法用时虽然大于MF、ATV和OGSTV，但都未超过8s，在可接受范围内。对比后发现，用时明显小于BM3D和KSVD，这是由于最后两种方法涉及到耗时的非局部块匹配和字典训练。

表1 针对四种含噪数据的六种方法去噪结果评价指标对比

图6展示δ=40时上述六种方法去噪结果。强噪声背景下，ATV(图6a)去噪并不理想，残留明显斑点和小块，阶梯效应严重。OGSTV(图6b)引入邻域信息，阶梯效应得到一定压制，但仍存部分斑点伪影。MF(图6d)去噪效果最差，存在大量残余噪声。BM3D(图6e)产生了平滑效应，对深层弱信号的保护能力差。KSVD(图6f)存在一定斑点，影响了最终去噪效果。图6c所示剖面干净，阶梯效应弱，深层反射波同相轴连续性好，说明本文方法具有保护弱信号能力。

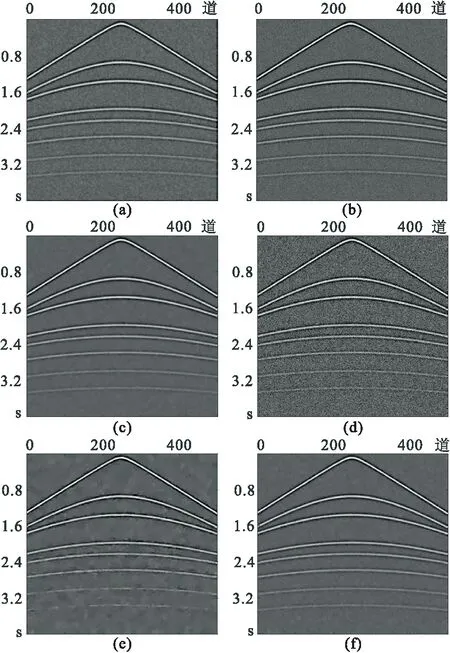
图6 不同去噪方法对比(a)ATV； (b)OGSTV； (c)本文方法； (d)MF； (e)BM3D； (f)KSVD

从上述不同方法纵横向对比可知，本文方法能有效去除随机噪声，压制阶梯效应，更好地保护弱信号，在效率与精度上能达到良好的平衡。

3 实际资料应用

将本文去噪方法应用于M工区实际地震资料。所选单炮记录(图7a)共有240道，采样点数为700，采样间隔为2ms。由于存在大量随机噪声，反射波同相轴连续性差，弱能量信号被掩盖，信噪比较低。其叠后剖面(图7b)共有800道，采样点数为800，采样间隔为2ms。该剖面深部地层有一定起伏，且发育微断层。随机噪声的存在致使剖面不清晰，同相轴错断，给地质解释带来诸多不便。

分别用上述六种方法进行去噪处理并得到图8(单炮)和图9(剖面)所示结果。历经多次试验并优选，针对图7所示实际资料，本文方法参数设置为K=4、p=0.18和K=3、p=0.21。对比所得单炮记录去噪结果可知，ATV(图8a)和MF(图8d)去噪效果差，信号失真严重，尤其是1.2～1.5s和2.1～2.5s区间的弱信号；相对而言，OGSTV(图8b)阶梯效应明显减少，去噪效果有一定提升，但仍存残余噪声； BM3D(图8e)能保留强能量信号，但弱信号恢复能力差，产生了严重的平滑效应； KSVD(图8f)和本文方法(图8c)去噪效果相对较好，但KSVD在一些细节(弱信号)上不如本文方法。

图7 原始地震资料(a)单炮资料； (b)叠后剖面

图8 不同单炮记录去噪结果对比(a)ATV； (b)OGSTV； (c)本文方法； (d)MF； (e)BM3D； (f)KSVD

对比、分析图9及表2可知，MF去噪效率高，但剖面(图9d)上仍有大量噪声残留； OGSTV(图9b)去噪效果有改善，但仍不理想； ATV(图9a)去噪后产生的阶梯效应使部分细节丢失；同样地，BM3D(图9e)出现平滑模糊区块，不利于微断裂等信息的恢复； KSVD(图9f)和本文方法(图9c)都有效压制了随机噪声，但KSVD计算效率低。