透视三点问题的一种快速且稳定的代数解法

耿庆华 刘伟铭

(华南理工大学 土木与交通学院，广东 广州 510640)

透视n点(PnP)问题被认为是使用图像坐标系和世界坐标系之间的n个对应的控制点来估计已校准摄像机的旋转角度和位置关系。PnP问题已广泛用于摄影测量[1]、机器人定位[1]、摄像机校准[2]、姿势估计[3- 4]、增强现实、地铁和自动驾驶中的自动视觉检查等。在过去的几十年中，已有各种解决方案来解决PnP问题，例如最小二乘法、迭代法[5]、代数法[6]和几何方法[7]。这些方法极大地提高了相机的性能。作为PnP问题的最小子集，透视三点(P3P)问题是一个最基本的问题[7- 8]。因此，当图像坐标系和世界坐标系之间的对应点不足时，P3P问题的求解方法对于估计摄像机的旋转角度和相对位置起到了关键作用。P3P问题最早是由Grunert[9]提出的。许多研究人员为解决P3P问题付出了巨大的努力，并提出了许多方法。Haralick等[10]对P3P问题进行了总结与回顾，并仔细验证了文献[1，8- 9]中算法的稳定性。Bujnak等[11]采用Gröbner基作为方程求解器，以边长比为约束条件，减少了未知参数的数量，获得了焦距未知的P4P通用解。Linnainmaa等[12]提出了一种新的P3P问题求解方法，用来估计一个在图像中形状已知的物体的三维位置和方向，即通过使用广义的Hough变换，将物体上点的三元组与图像中可能对应的三元组匹配来确定值的分布，以此估计物体位置的6个参数。Su等[13]采用Wu-Ritt’s消元法获得了P3P问题的主要解以及一些非退化解，然后采用斯图姆(Sturm)序列得出了判定P3P问题正解个数的充要条件。Quan等[6]回顾了透视三点问题代数解法，并提出了一种线性方法，当控制点达到5个以上时，该线性方法可以获得一个特解。Gao等[14]采用Wu-Ritt’s消元法第一次给出了多项式方程组完整的三角分解，而且给出了用于判断完整根的个数的判定条件，但该算法计算过程复杂，导致计算效率低下。Wu等[15]利用正交变换求解正解等价于求解基于变换定义的旋转矩阵和平移向量[16]，但只给出了解的上限，并没有进行详细的证明。总的来说，这些方法具有多解，或者在某些情况下根本没有解。大多数经典的P3P问题求解法都采用了余弦定律，并采用两个步骤来求解[17]。首先，这些方法确定从相机中心到三维(3D)控制点的距离，利用余弦定律可得到二次方程。除了一些特殊情况，一个三元组的二次方程最多可以获得4个解[4,17]。其次，这些方法通过对齐世界坐标系和相机坐标系中描绘的三角形来估计出已校准相机的旋转角度和相对位置。Kneip等[18]针对一个特定的角度，使用复杂的几何变换来构造3个二次方程式，消去中间变量，获得一个只有一个未知参数的四次方程，从而求得P3P问题的封闭解，但其复杂的几何变换在一定程度上不仅削弱了算法的性能，而且导致计算效率低下。Li等[19]利用相似三角形提出了一种P3P问题的透视相似三角形(PST)算法。PST算法在排序问题和图像噪声存在的情况下获得了很高的稳定性，而且不依赖于特定的方程求解器，即使在“危险圆柱体”(P3P的一种典型的几何奇点)中也可以获得可靠的结果。然而，PST算法并不是直接求解算法，因为PST需要构造一个透视图三角形。胡钊政等[20]提出了透视三点问题贝叶斯解法(BP3P)。该方法不仅能求解P3P问题，还能进一步分析P3P问题解的分布情况。该方法首先将P3P问题转化为支撑平面的计算问题。支撑平面的计算可以利用3个三维控制点产生的角度、长度和比例等约束条件，通过贝叶斯理论转化成最大似然概率估计问题，该方法通过搜索高斯半球面来计算最大似然概率，确定支撑平面结构信息，完成P3P问题的求解，并对P3P多解现象进行分析[20]。王波等[21]提出了一种根据本质二次曲线的交点判断P3P问题解的个数的方法。P3P问题的解与由其基本约束方程式导出的2条二次曲线在第一象限内的交点之间存在一一对应的关系。通过判断两条二次曲线交点的个数，可直观地确定P3P问题解的个数。Ke等[22]提出了一种有效的P3P问题的代数求解方法，该方法首先使用相应的几何约束来建立三角方程组，进而直接确定相机的姿态，然后通过代数求解方式确定未知的摄像机的旋转矩阵及位置。Persson等[23]提出了一种精确、快速、鲁棒的P3P问题求解法。该方法利用基本的椭圆方程，通过快速且数值精确的对角化来求解。这种对角化需要一个三次方根，用于查找最多4个P3P问题的解。Wang等[24]提出了一种计算效率非常高的P3P问题的求解方法，该方法利用中间坐标系变换简化了P3P问题的计算模型，从而提高了计算效率。

当控制点的Z轴坐标在相机坐标系的较宽范围内随机分布时，上述P3P问题的求解方法随高斯图像噪声的增加，其旋转矩阵和平移矢量的标准误差出现了峰值，这是由异常值结果导致的，且误差较大。基于上述分析，本文提出了一种快速且稳定的P3P问题的代数求解方法，该方法通过引入一个中间坐标系来简化P3P问题的求解过程。本文选取两个控制点的中心作为中间坐标系的原点，以提高P3P问题求解方法的稳定性以及在退化配置中的抗噪性能；引入两个辅助变量，将P3P问题简化为一个四次方程式，通过该方程式求得相机位姿的封闭解。最后通过计算机仿真，对文中提出的方法与其他3种经典的P3P算法(Wang的方法[24]、Gao的方法[14]和Kneip的方法[18])进行了对比实验，并比较分析了实验效果。

1 代数求解方法

1.1 问题描述

首先使用针孔模型作为摄像机模型，并且假定摄像机已校准。摄像机的图像平面有两条垂直轴，它们穿过图像中心。焦距是从光学中心(透视投影的中心)到图像中心的距离，设为1，则图像平面变成了归一化的图像平面。在摄像机模型使用针孔模型的前提下，透视三点问题定义为：在已知的世界坐标系下，3个空间控制点在世界坐标系的坐标及其在像平面上的对应坐标已知，且摄像机的内参数已标定的前提下，求摄像机在世界坐标系的位置与姿态。

图1 参考点在像平面上的透视投影

1.2 旋转角度和相对位置的估计

本文选择一个基坐标系来描述空间中任何物体的位置，并以该基坐标系来描述摄像机的位置，该坐标系称为世界坐标系(OwXwYwZw)，由Xw、Yw和Zw轴组成。世界坐标系与摄像机坐标系之间的关系可以通过旋转矩阵Rwc和三维平移矢量Twc来描述。假如空间中任一点P在摄像机坐标系与世界坐标系下的坐标分别是(Xc,Yc,Zc)和(Xw,Yw,Zw)，于是存在如下关系：

(1)

其中，Rwc为正交单位矩阵，Twc为三维平移矢量，Rwc和Twc可以分别参数化为

(2)

其中，(u,v)为p点在像平面上的坐标，f为摄像机焦距。由于文中已设定焦距f=1，若用齐次坐标与矩阵表示上述透视投影关系，则式(2)可以简化为

(3)

将式(1)代入式(3)，可得如下关系式：

(4)

综上分析，若直接求解旋转矩阵Rwc和平移矢量Twc，那么需要求解12个未知参数(r1,r2,…,r9和tx、ty、tz)，计算过程十分复杂。为了简化计算，文中引入一个新的坐标系，称为中间坐标系，如图1所示。中间坐标系相对于摄像机坐标系的旋转矩阵和平移向量分别定义为Rmc和T，并参数化为

(5)

(6)

(7)

重新调整参数，得到

Mα=0

(8)

其中，α=[R1,R4,R3,R6,Tx,Ty,R7,R9,Tz]T，M=

矩阵M的所有分量都是已知的，而向量α由9个未知参数组成，需要确定。矩阵M的秩为6，小于未知变量的个数9，因此不可能获得唯一解。但方程式(8)具有9-6维的基础解系，其任何线性组合都满足方程式。在上述情况下，6×9矩阵M是3个向量α1、α2、α3的零空间矩阵，并且α1、α2、α3彼此线性独立。满足等式(8)的解α一定可以由α1、α2、α3线性表示：

(9)

此时未知参数的数量减少到3。通过表达式αi=(αi1,αi2,αi3)，Ri可以表示为

(10)

(11)

至此，将问题转换为3×3×3张量方程[25]。

1.3 旋转矩阵和平移向量的估计

将式(8)的系数矩阵M分为两个矩阵，即M=(A|>B)，其中A部分是6×6矩阵，B部分是6×3矩阵。显然，A是一个可逆矩阵，可通过以下方式求得零空间的3个向量，即

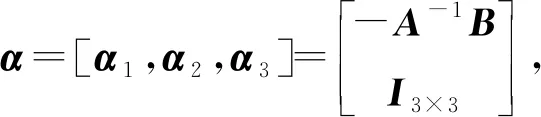
(12)

(13)

将式(12)代入式(13)并重新安排各项参数，得到

(14)

根据等式(14)中的第二个约束，可以得到

(15)

将式(15)代入式(14)中的第一个约束，可得

f4θ4+f3θ3+f2θ2+f1θ+f0=0

(16)

θ可以从等式(16)获得，该式最多有4个解。将θ代入式(15)可获得ω，通过方程(12)得到{ω，θ}和ri后，可以确定

根据式(9)可直接确定α的其他分量。(R2,R5,R8)T可以通过(R1,R4,R7)T×(R3,R6,R9)T来计算。Rwc和Twc可由Rmc和T确定，即

Rwc=RwmRmc，

Tmc=T-RwmRmcOm。

2 实验及结果分析

为评估本文算法的性能，采用具有640×480像素的图像尺寸和800像素焦距的虚拟透视相机进行实验，并对比分析了本文算法与文献[14,18,24]算法的实验结果。假定照相机的主点位于图像中心，3个控制点在相机坐标系中随机分布在[-2,2]×[-2,2]×[2,80]的范围内。在2D像平面没有添加噪声的情况下，4种算法各运行执行了60万次运算，实验结果如图2所示。从0像素到5像素的高斯白噪声被添加到2D像平面后，对不同的图像噪声进行了2 000次测试，结果如图3所示。

图2 4种算法的数值稳定性比较

从图2可知，本文算法的误差直方图在最小误差区域的集中度更高。这表明，所提出的算法具有更好的数值稳定性。

从图3可知：在计算旋转矩阵和平移矢量时，本文算法的标准误差随高斯图像噪声线性增加的幅度较小且没有出现峰值，而其他3种算法增加的幅度较大，甚至出现了峰值；4种算法的平均误差比较接近，均随高斯图像噪声的增加而增加，但本文算法增加的幅度相对较小。这表明本文算法在计算旋转矩阵、平移矢量时的抗噪性能更好，在退化配置中的抗噪声干扰能力更强。

4种算法在Matlab中各执行(主机配置为Intel Core i7、3.5 GHz，8 GB RAM)1 000次，通过电脑上测量1 000次运行的平均计算时间，可以获得运行时间的相对准确值，从而减轻量化误差和其他任何由计算开销引起的误差的影响。此外，在不同平台上进行计算的时间可能会有所不同。本文算法、文献[24]算法、文献[18]算法与文献[14]的算法的平均运算时间分别为1.977 7×10-5、1.963 0×10-5、2.371 0×10-5和3.961 8×10-5s。在算法的计算效率方面，本文算法与文献[24]的算法几乎相同，但与文献[14，18]中算法相比，大大减少了执行时间。

(a)旋转矩阵

(b)平移矢量

3 结论

当3D控制点的Z轴坐标在相机坐标系内大范围随机分布时，针对传统P3P问题的经典算法存在数值稳定性差、对图像噪声敏感、计算效率低的问题，本文提出了一种快速且稳定的代数求解方法。实验结果表明：本文算法的数值稳定性及在退化配置中的抗噪性能优于其他3种算法；当3D控制点的Z轴坐标在相机坐标系内大范围随机分布时，本文算法以相当低的计算成本保证了计算的精度和准确性。