某磁浮大跨斜拉桥竖向刚度限值研究
2021-02-04郑晓龙陈星宇徐昕宇宋晓东游励晖
郑晓龙,陈星宇,徐昕宇,宋晓东,游励晖
(中铁二院工程集团有限责任公司,四川 成都 610031)
磁浮交通是城市轨道交通领域中的一种新型交通模式,列车通过直线电机驱动,依靠悬浮架与轨道之间的电磁力实现列车的悬浮和导向。与普通轮轨交通相比,磁浮交通的行驶噪声低、运行振动小,且易于维护。此外,磁浮列车运行时无轮轨接触,因而不存在轮轨间黏着系数对列车牵引力的不利影响,显著提升了磁浮列车的爬坡能力和转弯半径适应范围。上述优点使得磁浮交通成为未来轨道交通发展的一个重要方向[1]。
目前磁浮轨道交通的商业运营线还很少,仅有日本东部丘陵线、长沙磁浮快线、北京轨道交通S1 线等。现有磁浮交通设计规范仅适用于中小跨度桥梁,规范对桥梁结构的变形和竖向刚度要求极为严格,对于大跨桥梁的结构形式、刚度限值还缺乏设计指引和技术标准。针对长沙某磁浮(85+110+85)m 连续梁桥的研究表明,若刚度控制指标采用简支梁的控制标准,将出现建设成本高、景观效果差的问题[2-5]。目前对磁浮大跨桥梁的刚度限值研究较为少见,亟须开展相关研究,为磁浮大跨桥梁设计提供科学依据。
本文以某中低速磁浮线的(40+80+228+228+80+40)m 斜拉桥设计方案为研究对象,建立全桥有限元模型及磁浮列车多体动力学模型,进行不同车速、不同梁高的车桥耦合动力仿真分析,进行主梁不同竖向刚度下桥梁及车辆的动力响应及中低速磁浮大跨桥梁的竖向刚度限值研究。
1 工程概况
本文研究的(40+80+228+228+80+40)m钢箱梁斜拉桥位于设计时速120 km 的某磁浮线路,线间距为4.4 m。该斜拉桥的梁宽为12 m,主梁断面形式如图1 所示。桥塔设计为H 型,塔全高60 m,主梁以上高34 m,横桥向宽4 m,顺桥向宽7 m,采用单箱单室截面,C55 混凝土。斜拉索采用1 670 MPa 级平行钢丝束,呈对称扇形布置,梁上索间距9 m,塔上索间距1.2 m。全桥效果图如图2所示,上方悬索桥为既有公路桥。

图1 主梁截面示意图

图2 全桥效果示意图
2 车桥动力分析仿真
磁浮列车—桥梁系统耦合振动模型由4 个子模型组成,分别是磁浮列车子模型、桥梁子模型、电磁铁系统子模型和悬浮控制系统子模型,如图3所示。

图3 磁浮列车—桥梁系统耦合模型
基于南车株洲厂磁浮车辆,采用多体动力学软件UM 建立磁浮列车子模型,模型中每节车体由5个电磁转向架构成,每个转向架的左右悬浮模块看成1 个整体模块对称分布,不考虑车辆的侧滚运动,1 个悬浮模块共有4 个电磁铁,转向架和车体之间的连接采用空气弹簧,将磁浮车辆组合成在轨道结构上运行的多刚体系统,考虑车体质量及其点头惯量、转向架质量及其点头惯量、空气弹簧的悬挂刚度和阻尼。车辆自由度包括车体的沉浮运动和点头运动、5 个转向架的沉浮运动和点头运动,整个模型共12个自由度[6]。
采用有限元软件ANSYS 建立桥梁子模型,桥梁结构按实际尺寸建立有限元模型,梁高考虑了4种高度,分别为2.5,3.0,4.0 和5.0 m,桥梁的阻尼比按0.5%选取。主梁和桥墩采用梁单元模拟。
梁部二期恒载按均布附加质量添加到梁单元中,墩梁间支座采用主从约束处理,该模型总共705 个节点,710 个单元,有限元模型如图4 所示。不同梁高时全桥基频结果见表1。

图4 全桥有限元模型

表1 不同梁高全桥基频
电磁铁系统子模型如图5 所示,电流在通过恒流线圈时,根据电磁感应定律,在电磁铁中产生电磁场,由电磁场产生的电磁力保证磁浮车体的悬浮状态。输入的电压经过一定的控制,并输入到电流线圈中产生电流,这样受控制的电压可以对控制线圈的电流也加以控制,从而产生受控制的电磁力,通过受控制的电磁力调整悬浮间隙。

图5 电磁铁系统模型
悬浮控制系统是根据产生悬浮间隙信号生成控制电压,控制过程则是根据在电磁铁两端的传感器的反馈信号,根据设置的控制算法产生控制电压,控制电压输入到电磁回路中产生一定的电磁力,以保证悬浮间隙在适当的范围内变化,达到控制器控制的效果。采用PD 控制方法模拟悬浮控制系统[7-8]。
仿真时,采用联合仿真技术,将ANSYS 软件建立的桥梁有限元模型导入多体动力学软件UM中,以悬浮控制系统作为相互反馈作用的关联,将磁浮列车、桥梁、电磁铁作为耦合体系,求解桥梁和磁浮列车的动力响应,如动位移、加速度、悬浮间隙等,并进行相应评价[9-10]。以车辆前进方向为纵向,轨道平面上与纵向垂直的方向为横向,垂直于轨道平面的方向为垂向。磁浮车辆、轨道及桥梁结构的振动往往由轨道不平顺引起。参考Hul⁃lender,Snyder 等提出的柔性高架线路采用的轨道随机不平顺功率谱[11-12],基于三角级数法,将功率谱密度函数转换为本文车桥耦合分析所用的磁浮线路高低不平顺数据曲线,如图6所示,轨道不平顺样本的长度1 000 m,竖向不平顺幅值为3.7 mm。本文中悬浮间隙δ设定为10 mm。
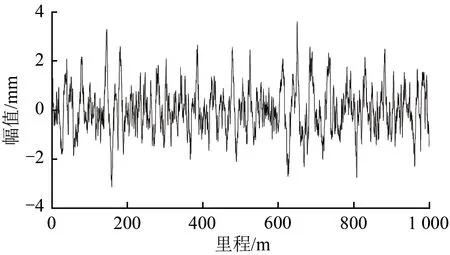
图6 轨道高低不平顺
3 车桥动力响应评价指标
对于车辆运行安全性与舒适性的评定标准依据GB 5599-1985《铁道车辆动力学性能评定和试验鉴定规范》,车体加速度按竖向≤0.15g、横向≤0.10g,舒适性Sperling 指标按优<2.50、 良2.50~2.75、合格2.75~3.00 评定。桥梁动力响应限值选取依据CJJ/T 262-2017《中低速磁浮交通设计规范》、铁运函〔2004〕120 号《铁路桥梁检定规范》等相关标准,设定桥梁动力响应为连续梁竖向挠度限值L/4 600(L为桥梁跨度);桥梁梁端水平折角限值1.5‰;桥梁竖向振动加速度限值0.50g(半幅)、横向振动加速度限值0.14g(半幅)[13-14]。
4 车桥系统动力响应
仿真分析中,单列列车采用6 节车编组,每节车重35 t,运行速度范围为1~140 km·h-1,选取2 列磁浮列车相向行驶并在斜拉桥左侧主跨跨中交会的最不利情况作为分析工况。
4.1 列车运行速度对车桥系统动力响应的影响
针对梁高为5 m 时的桥梁结构,开展列车运行速度对车桥系统动力响应影响的分析,磁浮列车和桥梁结构的竖向动力响应结果见表2。

表2 梁高为5 m时不同车速下车桥动力响应结果
由表2 可见:在车速为1~140 km·h-1范围内,梁体竖向位移的变化幅度约为3 mm;梁体的竖向位移和梁端竖向折角受车速变化影响较小,梁体的竖向加速度变化较为显著,但最大值仅为0.068 m·s-2,远小于梁体竖向加速度限值;磁浮列车的竖向动力响应均随着列车车速的增大而增大,且增幅明显。
后续针对140 km·h-1车速情况下梁体刚度与列车竖向动力响应的关系开展分析研究。
4.2 梁体高度对列车系统动力响应的影响
4.2.1 列车竖向加速度
140 km·h-1速度下,不同梁高时的梁体挠跨比及磁浮列车竖向加速度响应结果见表3。

表3 不同梁高时梁体竖向挠跨比及磁浮列车竖向加速度(车速为140 km·h-1时)
由表3 可见:随着箱梁高度的增大,竖向挠跨比显著减小,磁浮列车的车体竖向加速度响应减小趋势明显;梁高为2.5 m 时,梁体竖向挠跨比达到1/2 129,磁浮列车竖向加速度为1.126 m·s-2,仍满足要求,且有一定富余量,说明车体竖向加速度不是该中低速磁浮大跨桥梁结构刚度限值的控制因素。
4.2.2 列车竖向Sperling指标
表4 给出了列车在140 km·h-1速度下,不同梁高时梁体竖向挠跨比及列车车体竖向Sperling指标。
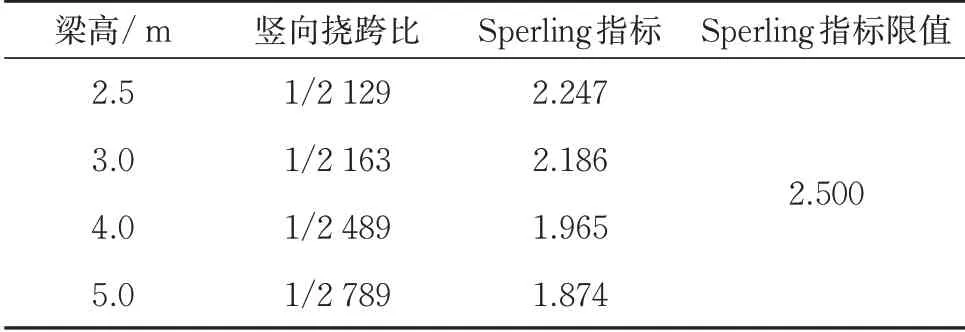
表4 不同梁高时梁体竖向挠跨比及磁浮列车竖向Sperling指标(车速为140 km·h-1时)
由表4 可以看出:车体竖向Sperling 指标随着梁高增大而明显减小;梁高仅2.5 m 时,梁体竖向挠跨比达到1/2 129,列车的Sperling 指标为2.247,仍然达到“优秀”,各刚度水平下列车的Sperling 指标均在“优秀”,说明车体竖向Sperling指标也不是该中低速磁浮大跨桥梁结构刚度限值的控制因素。
4.2.3 列车悬浮间隙
140 km·h-1速度下,不同梁高时梁体挠跨比及磁浮列车悬浮间隙见表5。
由表5 可以发现,不同于列车的竖向加速度和Sperling 指标,列车的悬浮间隙随梁高变化显著。对比可知,当梁高较小时,磁浮列车的悬浮间隙的最值已经非常接近于0 和20 mm,即存在车体与轨道接触碰撞的较大可能性。随着梁高的增大,梁体刚度逐步提高,悬浮间隙的波动范围明显减小,悬浮间隙的最值与额定悬浮间隙的差距变小。
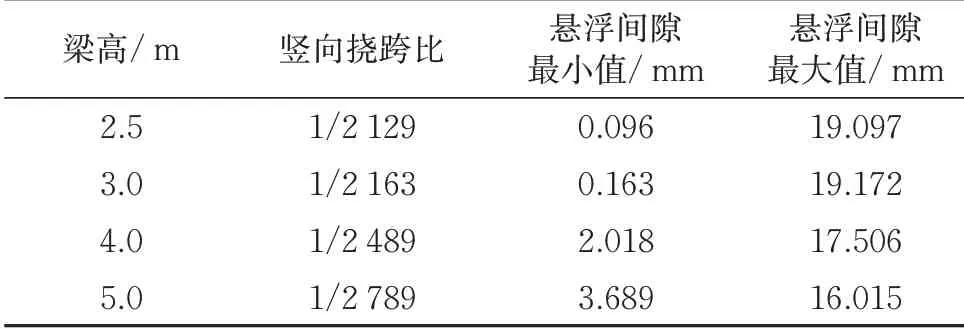
表5 不同梁高时梁体竖向挠跨比与磁浮列车悬浮间隙(车速为140 km·h-1时)
由此可见,磁浮列车的悬浮间隙对梁体刚度变化较为敏感,当梁体刚度较小时,悬浮间隙波动明显,说明列车的悬浮间隙可作为该中低速磁浮大跨桥梁结构刚度限值的控制指标。
5 竖向刚度限值
由前述分析可得,对于该中低速磁浮大跨度斜拉桥,磁浮列车的悬浮间隙是桥梁结构刚度限值的控制指标。根据分析结果,对该中低速磁浮大跨度桥梁梁体挠跨比限值进行分析。图7给出了不同梁高时梁体的挠跨比及磁浮列车的悬浮间隙。

图7 不同梁高时梁体刚度及磁浮列车悬浮间隙
由图7 可见,以5~15 mm(δ±δ/2)为悬浮间隙的容许安全波动范围,当梁高为5 m、竖向挠跨比为1/2 789时,悬浮间隙仍不满足要求。因此,采用样条插值方法,对竖向挠跨比、悬浮间隙最大值以及最小值分别进行非线性外插,当悬浮间隙最大值和最小值均在容许波动范围内时,此时的梁体竖向挠跨比即为满足磁浮列车行车性能要求的临界值。通过上述分析,得到梁体竖向挠跨比临界值为1/3 015。
6 结 论
(1)该中低速磁浮大跨度斜拉桥的桥梁动力响应在1~140 km·h-1车速范围内均满足要求。
(2)对于不同竖向刚度方案,即使梁体竖向挠跨比达到1/2 129,列车的车体竖向加速度和Sperling 指标均满足要求,且富余量较大,说明车体竖向加速度和Sperling 指标不是该中低速磁浮大跨桥梁结构刚度限值的控制因素。
(3)当梁体刚度偏小时,列车悬浮间隙将超出容许值范围,影响行车安全;随着梁体刚度逐步增大,悬浮间隙距离稳定悬浮间隙值的波动变小,梁体挠跨比减小约25%,悬浮间隙波动减小幅度达到35%。因此,悬浮间隙可作为该中低速磁浮大跨桥梁结构刚度限值的控制指标。
(4)对于该中低速磁浮大跨度桥梁的竖向刚度,根据仿真分析结果,可将梁体挠跨比控制在1/3 015以内。
