基于代价敏感卷积神经网络的扣件缺陷检测算法

侯 云，范 宏，熊 鹰，李 立，李柏林

（西南交通大学 机械工程学院, 四川 成都 610031）

扣件作为连接钢轨与轨枕的重要部件，起着固定钢轨的作用。列车在运行过程中产生的异常振动可能导致扣件发生断裂或者脱落。这些情况如不能及时地处理，可能影响扣件功能和列车运行安全。传统的扣件检测方法主要依靠人工进行检测，该方法效率低，很难满足现代高速铁路的需求。

国内外许多学者将图像处理技术引入到扣件检测领域，并提出了诸多自动检测算法。文献［1］依据铁路各部件先验位置关系定位出扣件子区域后，利用小波变换、结合PCA 降维对扣件子区域进行特征提取，并将所提特征输入到RBF 神经网络和BP 神经网络中进行分类。文献［2］依据先验位置关系确定出扣件子区域后，利用Daubechies小波和Haar 小波对扣件子区域提取特征，并将所提特征输入到多层感知器神经分类器中进行分类。文献［3］将扣件子区域的方向场作为特征，并在此基础上利用模板匹配的方法对扣件状态进行识别。文献［4］利用垫板位置定位扣件子区域，然后分别对扣件关键部位提取PHOG 和MSLBP特征并将其进行融合，最后使用支持向量机对融合特征进行分类。文献［5］根据轨枕与钢轨的相对位置定位扣件子区域，继而分别对4个扣件关键部位提取Haar-like 特征，并将所提特征输入到AdaBoost分类器进行分类。文献［6］利用钢轨和轨枕的边缘直线特征定位扣件子区域，并将子区域的Haarlike 特征与概率主题模型结合检测扣件状态。文献［7］利用垫板位置定位扣件子区域，并基于扣件子区域的边缘特征实现扣件的缺失检测。文献［8］通过构建扣件邻域纹理图和引导图与被定位图之间置信图的极大值点快速定位扣件子区域，并基于半监督深度学习方法建立扣件缺陷识别模型，实现无砟轨道扣件缺陷样本识别。文献［9］根据轨道图像的先验知识和模板匹配方法定位扣件区域，并利用深度卷积神经网络实现扣件缺陷识别。文献［10］利用模板匹配以及扣件先验位置关系定位扣件子区域，并以2 个相邻扣件子区域的特征差值作为依据检测扣件缺失状态。上述扣件检测方法均是在人为选定的小批量、各类样本均衡的扣件数据集上进行的试验。由于小批量的均衡数据集不能很好地体现实际扣件数据集的数据分布，这些传统的扣件检测方法的适应性往往较差。在实际情况中，扣件断裂或者丢失的情况很少发生，这导致所收集的扣件数据集中断裂或丢失的缺陷扣件样本数远小于正常扣件样本数。这种现象称之为类不平衡，其中缺陷扣件称之为小类，正常扣件称之为大类。在扣件检测算法中，研究者往往更关注扣件断裂或丢失的小类情况。

近年来，深度卷积神经网络（Convolutional Neural Network，CNN）作为一种非常流行的方法，在很多领域都有应用［11-13］，并取得了较传统分类器更好的识别效果。卷积神经网络避免了复杂的图像特征提取过程，可以直接输入原始图像进行处理。深度卷积神经网络是在大批量且分布相对均衡的图像训练集上，以最小化训练集的整体误差为目标构建最优分类模型。对于不平衡数据集而言，这往往会导致分类器倾向于将断裂或者丢失的扣件误认为是正常扣件。因此，直接将深度学习算法应用到不平衡的扣件数据集是不合适的。目前，一些学者将代价敏感策略引入到深度神经网络中，通过给小类分配较大的代价因子的方式提高小类样本的识别率［14-16］。但是，这些方法都没有考虑同一类别中不同样本个体之间存在的差异。在实际分类中，扣件的断裂程度不同，其识别的难度也会不同。如果分类器不考虑类别内样本间客观存在的这种差异，往往会降低最终模型的识别率。

本文针对扣件数据集不平衡问题，借鉴Ada⁃Boost 算法的思想，对深度卷积神经网络进行改进，提出一种同时关注类别间差异和类别内差异的基于代价敏感卷积神经网络的扣件缺陷检测算法。

1 代价敏感策略

卷积神经网络的核心是利用反向传播算法最小化训练集整体误差，以训练得到最优的网络模型。假设训练集X中有N个样本，这些样本可分为K个类别，即

式中：Xcj为第j类的样本集合；Nj为第j类的样本个数。

训练集整体误差E为

式中：Xi为训练集中第i个样本；E（Xi）为训练集中样本Xi的误差。

由式（3）可见，CNN 的整体误差是所有训练样本误差的平均值。对于扣件这种不平衡数据集而言，由于断裂或丢失的扣件样本较少，这类样本在整体误差函数中只占很小的比重，这很容易导致最终得到的神经网络模型偏向于正常样本。为了克服传统神经网络的这一缺陷，代价敏感策略［14-16］将代价矩阵引入到神经网络中，对不同类别分配不同的惩罚因子，使算法偏向于小类样本。目前，这些已提出的代价敏感策略只考虑不同类别样本之间的差异，并没有考虑同一类别中不同个体之间的差异。以扣件图像为例，图1 为2 个断裂程度不同的扣件样本，断裂程度相对较小的扣件所提特征往往处于分类边界附近，处于分类边界处的样本要比远离边界的样本更难学习，却对确定分类边界起着更为重要的作用。

图1 2种不同断裂程度的扣件

AdaBoost 算法［17］是一种增强困难样本学习的有效方法，其思想是通过给错误学习的样本分配更大权重的方式，使后续学习过程关注那些更难学习的样本。受AdaBoost 算法启发，本文提出一种代价敏感卷积神经网络算法，使训练网络在考虑类别间差异的同时增强类内难样本的学习。与传统代价敏感策略不同，本文算法在训练过程中给每个样本分配不同的权重，并在后续学习中依据先前网络的错误率不断地调节这些权重。其目的是使每个类别中分类错误的样本比分类正确的样本具有相对更大的权重，从而使后续训练的神经网络关注各个类别中的难学习样本。与此同时，本文算法对更新后的各类样本权重进行了特殊的归一化处理，以便提高缺陷样本的关注度。为实现上述步骤，本文将训练集整体误差函数式（3）修改为

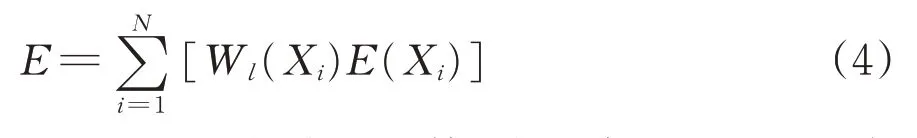
式中：Wl（Xi）为样本Xi在第l次迭代时的权重；当l=0时，W0（Xi）为初始权重。

在AdaBoost 算法中，每个样本的初始权重都设置为1/N。而本文算法按照1 种非对称的方式将每类样本的初始权重W0对应地设置为

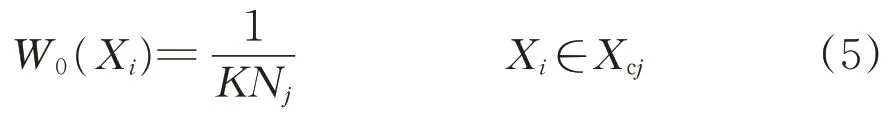
在计算完成1 次迭代之后，算法利用当前训练好的网络对训练集进行测试，并计算错误率ε为

式中：Nerror为识别错误的样本数。

当错误率ε小于0.5时，计算权重更新参数α为

每个样本在第l次迭代时的权重Wl按照下式更新。

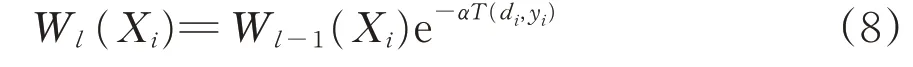
其中，

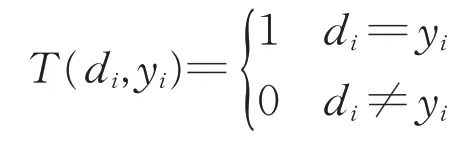
式中：yi为样本Xi的预测类别；di为样本Xi的真实类别。

由式（8）可见，当样本判断正确时，其权重缩小为原来的e-α；当样本判断错误时，其权重不变。

由式（4）可见，训练集整体误差是所有样本误差的加权和，由于正常扣件样本数量众多，这类样本势必要在整体误差函数中占主导作用，这往往会使得缺陷扣件样本在训练过程中被忽略，从而导致缺陷样本识别率低。为了增大缺陷样本在整体误差函数中的比重，提高对这类样本的关注度，本文算法对更新后的样本权重进行一个特殊的归一化处理，使每类样本的权重和为1/K。

不同于AdaBoost 算法，本文算法只选择最优训练模型作为最终的输出模型，而不是对所有弱分类器进行集成。

2 扣件缺陷检测的代价敏感卷积神经网络

以VGG19 网络作为基础网络，针对扣件数据集不平衡的特点，引入代价敏感策略设计扣件缺陷检测的网络结构，如图2 所示。由于扣件子区域为灰度图像，需要将网络第1层卷积核的颜色通道设置为1。由于扣件数据集只包括3 个类别，最后1个全连接层的神经节点数相应地设置为3，分别对应扣件正常、断裂和丢失3种状态。除此之外，其他与原始VGG19 网络保持一致。该网络由16 个卷积层和3个全连接层组成，每个卷积层的卷积核尺寸为（3×3）像素，步长为1 像素；池化操作的方式取最大值池化（Maximum pooling），窗口尺寸为（2×2）像素，步长为2 像素；激活函数采用修正线性单元（Rectified linear unit，ReLU）；每个卷积操作后采用批归一化处理（Batch normaliza⁃tion）；前2 个全连接层后使用随机失活（Dropout）策略。输入图像的大小为（180×180）像素，而扣件图像实际大小为（180×120）像素，需要将扣件图像进行插值运算以便适应该网络。

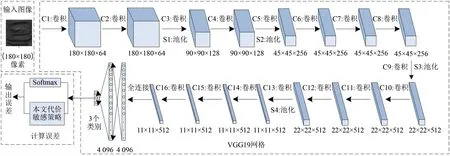
图2 基于代价敏感策略训练网络

为了增强网络对缺陷扣件的学习，将代价敏感卷积神经网络应用于扣件检测中，以减小样本数量失衡对识别性能的影响。修改后模型的训练过程主要分为3个步骤，具体如下。

步骤1：按照式（5）设置训练集中每个样本的初始权重；

步骤2：开始训练，迭代每完成1 次后，对训练集进行测试，统计错误率，调整每个样本权重并对其进行归一化处理；

步骤3：重复执行步骤2，直至所有迭代次数完成为止；

步骤4：结束训练，保存模型参数。

该网络采用随机梯度下降算法进行训练，样本批量大小为100个，迭代训练次数（Epochs）为80次，随机失活比例为0.5，动量（Momentum）为0.9，权重衰减因子为0.000 3。初始学习率为0.1，每迭代10次后学习率下降至原来的0.1。

需要说明的是，在本文算法中，训练集整体误差是由单个样本误差的加权和组成，因此其反向传播过程与原始VGG19网络算法一致。

3 试验验证

试验利用Python 软件开发，使用CUDA9.0，Tensorflow 等工具库。计算服务器采用1 块Intel Xeon Silver 4110 型CPU 和1 块NVIDIA GeForce GTX 1080 Ti型GPU计算卡。

3.1 试验数据集

利用文献［10］提出的扣件定位方法，分别截取高速铁路无砟和普速铁路有砟轨道的扣件子区域图像作为研究对象，验证算法的有效性。其中，高速铁路无砟轨道的扣件数据集由20 000 张扣件子区域图像组成，包括正常图像19 836张、断裂图像93张以及丢失图像71张。图像大小为（180×120）像素，如图3所示。

图3 高速铁路扣件典型样本

普速铁路有砟轨道的扣件数据集由20 000 张扣件子区域图像组成，其中包括正常图像19 334张、断裂遮挡图像503 张以及丢失图像163 张。图像大小为（180×120）像素，如图4所示。

本试验分别将2 个扣件数据集都平均分成5份，其中4份作为训练集，剩余1份作为测试集。

图4 普速铁路扣件典型样本

3.2 试验评价指标

平均准确率是传统分类中常用的评价指标。由于它可能会导致分类器忽略小类样本，这个评价指标已被证明不适用于不平衡分类［18］。例如，现有1个数据集包括999 个正样本以及1 个负样本，以准确率为导向的分类器会将所有的样本都认为是正样本，这样其准确率依然会达到99.9%，但是对于负样本而言其准确率却为0%。在实际应用中，往往扣件断裂或丢失的负样本才是更被关注的。为了克服平均准确率的缺陷，本文引入一种新的评价指标G-mean［16］来衡量分类器的分类性能。G-mean平衡了不同类别的召回率，当其中任意1个小类的召回率值为0时，最终的G-mean值为0。

其中，

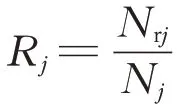
式中：Gmean为G-mean 值；Rj为第j类样本的召回率；Nrj为第j类中识别正确的样本个数。

3.3 试验结果

应用本文方法、原始VGG19 网络算法以及国内外其他3 种识别率较高的扣件检测算法对3.1 选取的高速铁路无砟和普速铁路有砟轨道扣件数据集进行识别，其结果见表1。

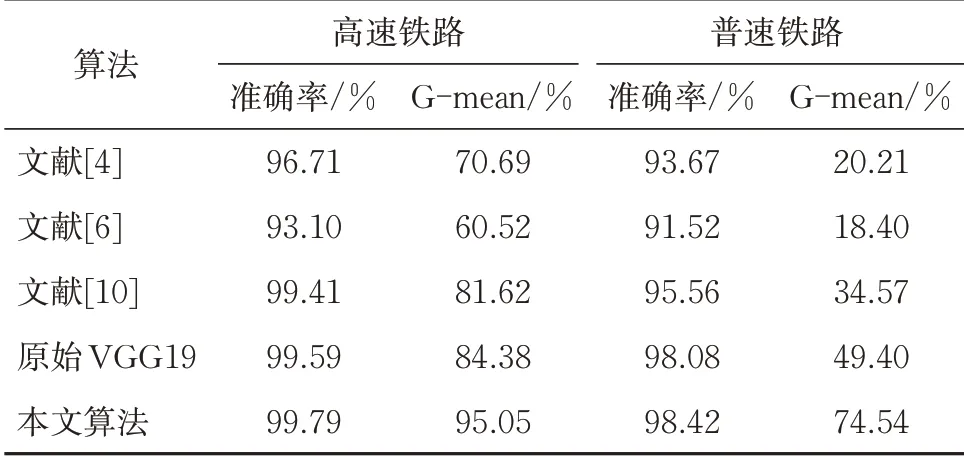
表1 扣件数据集试验结果

由表1 可知：在高速铁路无砟轨道扣件数据集上，本文算法与传统扣件检测方法相比，尽管准确率提高得并不明显（＞0.3%），但是却取得了更高的G-mean 值（＞13%）；在普速铁路有砟轨道扣件数据集上，本文算法取得比传统扣件检测方法更高的准确率（＞2%）以及G-mean 值（＞39%）。所有的算法在高速铁路无砟轨道扣件数据集上的分类性能均比在普速铁路有砟轨道扣件数据集上高，这是因为高速铁路无砟轨道扣件数据集不受道砟影响，背景情况单一；而普速铁路有砟轨道扣件数据集受道砟影响较大，背景较复杂。相比于原始VGG19 网络算法，本文算法在高速铁路无砟和普速铁路有砟轨道扣件数据集上分别提高了至少10%和25%的G-mean值。分析其原因为：

（1）扣件数据集中绝大多数的扣件是正常的，而断裂和丢失的扣件样本较少。传统的分类器往往人为构建一个小批量的均衡数据集来训练模型，而此类算法往往适应性较差。本文算法引入代价敏感策略来修改卷积神经网络模型中的训练集整体误差，并利用特殊的归一化方法增大断裂和丢失这类缺陷样本在整体误差中的比重，能够使算法偏向于这些小类样本。

（2）正常扣件和丢失扣件这2 类样本间的特征差异较大，容易被正确区分；而对于断裂扣件图像样本而言，其断裂程度越小，样本越难识别。本文算法在训练过程中给不同的样本分配不同的权重，并依据先前分类器的错误率不断地增加各个类别中难学习样本的权重，从而使算法更关注断裂程度小的扣件样本。

4 结 语

引入代价敏感策略对卷积神经网络进行修改，提出一种基于代价敏感卷积神经网络的检测图像识别计算方法，实现扣件缺陷检测。该方法增强了扣件数据集中难学习样本以及缺陷扣件类别的学习。通过对某高速铁路无砟及普速铁路有砟轨道的扣件数据集进行试验，发现修改后的算法在处理不平衡数据集方面取得了一定程度的提升，在高速铁路无砟和普速铁路有砟轨道扣件数据集上G-mean 值分别提高了10%和25%以上，这可为实际相关应用领域提供一定的技术支撑。