高铁CFG桩—筏复合地基固结解析解及特性

商拥辉，徐林荣，陈钊锋

（1.黄淮学院 建筑工程学院，河南 驻马店 463000；2.中南大学 土木工程学院，湖南 长沙 410075；3.中南大学 高速铁路建造技术国家工程实验室，湖南 长沙 410075）

高速铁路具有高平顺性、高舒适性等优势，其经济社会效益也显著，是各国客运铁路发展主要方向［1］。相比桥梁而言，高铁路基软土地基处理更为复杂，运营期沉降超限的概率更高。目前，高铁路基软土地基处理多采用桩—网复合地基［2］、桩—筏复合地基［3］与桩—板复合地基［4］。综合考虑经济、处理能力等综合因素，桩—筏复合地基在工程实践中占比较大［5］。2005年，桩—筏复合地基首次应用到京津（北京—天津）城际铁路软土试验段地基处理中，以桩作为竖向增强体，与桩间土、褥垫层和筏板共同组成承载体系［3，5］，在提高地基强度、减少压缩变形方面效果显著。目前，桩—筏复合地基已在武广（武汉—广州）客运专线［6］、沪宁（南京—上海）城际铁路［7］、京沪（北京—上海）高速铁路［8］等线路中广泛应用。探究桩—筏复合地基的相关技术与理论问题，一直是铁路科技工作者研究的重要课题之一。

国内外学者和专家对刚性桩—筏复合地基技术进行了大量研究，尤其在沉降特性［9］、工作性状［10］、设计计算理论［11］等方面取得了颇丰的成果，但对桩—筏复合地基的固结特性与机理研究尚不充分。高铁桩—筏复合地基多采用PHC 和CFG刚性桩，以往学者对其展开固结分析时，多将刚性桩复合地基视为桩弥散于桩间土中形成的均质复合材料，建立地基固结方程，并求得地基固结度的解析解［12］。此类方法常忽略PHC 和CFG 等刚性桩不透水或弱透水性（排水边界差异），其计算结果与实测值或数值结果存在一定差距。同时，根据桩刺穿软土层情况，可分为端承型桩和悬浮型桩，二者之间受力特点与排水途径存在客观差异，加固区桩间土固结特性不同。因此，刚性桩—筏复合地基固结理论亟待改进，具体表现在3个方面：无透水性或弱透水性的刚性桩的存在，对桩间土的固结速率有何影响；端承型或悬浮型刚性桩—筏复合地基，固结速率随置换率、桩土压缩模量比、加荷速率等地基设计参数的变化如何；如何确定各设计参数的适用范围。

本文以轴对称固结模型为研究对象，推导出端承型刚性桩—筏复合地基桩间土的固结方程，得到单级等速加载情况下地基固结解析解。在此基础上结合实际工程案例，研究设计参数（置换率、桩土压缩模量比、加荷速率）对地基固结特性影响及各参数的临界适用范围。研究成果对了解端承型刚性桩—筏复合地基固结特性，以及为达到控制沉降目的的设计参数选取，具有理论意义和工程实践价值。

1 CFG桩—筏复合地基固结方程建立

为便于建立地基固结方程，假设如下：桩完全打入硬土层，不考虑下卧硬土层的固结；桩间土完全饱和、均质，土中固体颗粒与水为不可压缩体；考虑CFG 桩为不排水桩体，桩间土仅发生竖向渗流，桩—土界面不发生渗流；地基土体渗流符合Darcy 定律，渗透系数和压缩模量在复合地基固结中保持不变；上部荷载在地基中引起附加应力沿深度保持不变；假设任一深度处桩—土等应变条件成立［13］。

结合CFG 桩—筏复合地基工作原理，选取典型单元体建立地基固结计算简化模型，如图1 所示。图中：d为CFG 桩径，m；de为单桩处理等效圆直径，m，当桩采用等边三角形、正方形和矩形布桩时，de分别取1.05S，1.13S和1.13（S1S2）-1，S为等边三角形和正方形布桩时的桩间距，S1和S2为矩形布桩时的纵向桩间距和横向桩间距，m；Z为土体深度，m；H为桩—筏复合地基厚度，即桩长，m。

图1 计算简化模型图

图2 为桩—筏复合地基固结分析时的桩—土受力简化图。图中：σp和σs分别为桩体和桩间土内的平均附加应力，kPa；σ（t）为上部荷载在地基内引起的附加应力，为如图3 所示的随时间t变化的函数。

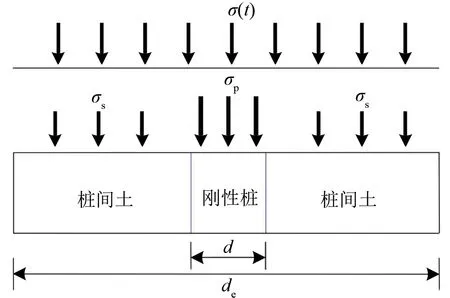
图2 桩—土受力简化图

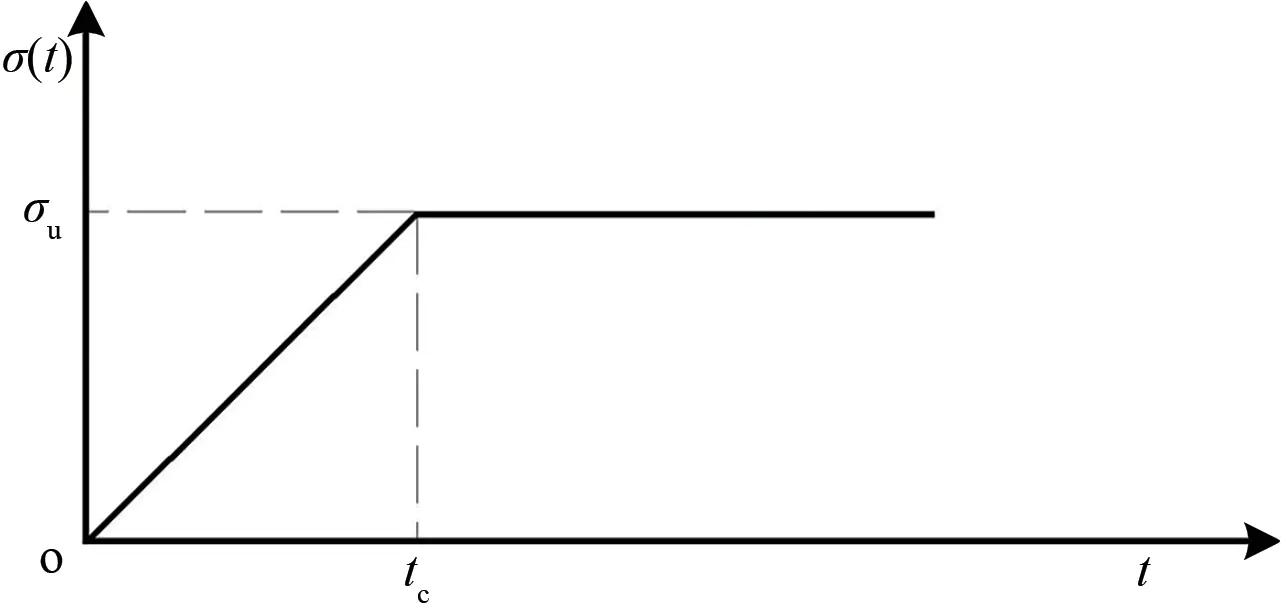
图3 地基附加应力—时间变化曲线

图中：σu为σ（t）的最终值，kPa；tc为加载时长，d，给定σu时，tc越小表示加荷速率越大。

对于复合地基内任意深度，由力平衡方程可得

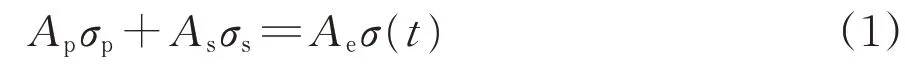
其中，

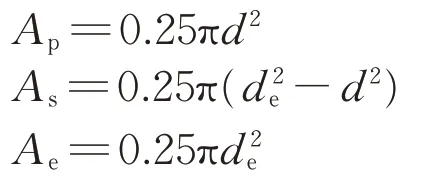
式中：Ap为刚性桩的截面积，m2；As为桩间土单元的截面积，m2；Ae为整个轴对称单元体的截面积，m2。

由等应变假定可知

式中：us为桩间土内任一深度、任意时刻的超静孔隙水压力，kPa；Ep和Es分别为桩体和桩间土的压缩模量，MPa；εv为桩体和桩间土在任一深度处的竖向应变。

由式（1）和式（2）有

其中，

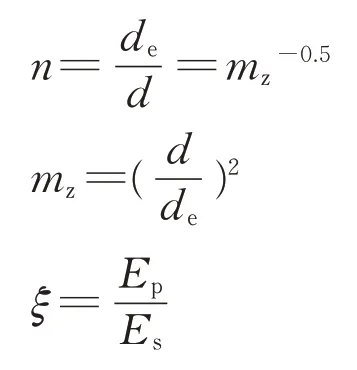
式中：n为井径比；mz为桩—筏地基置换率；ζ为桩—土压缩模量比。

竖向应变εv关于时间t的偏导数为

因桩间土只发生竖向渗流，则

式中：kv为桩间土的渗透系数，m·d-1；γw为水的重度，N·m-3。

由式（4）和式（5）得桩间土固结方程为

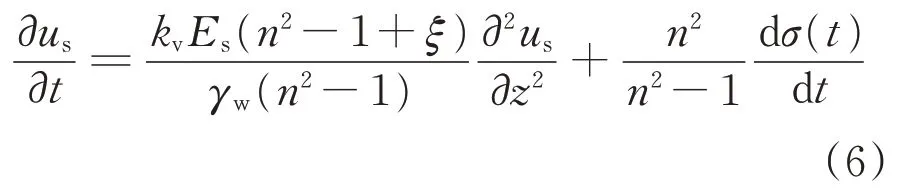
令为复合地基的等价固结系数，cm2·s-1，即

其中，

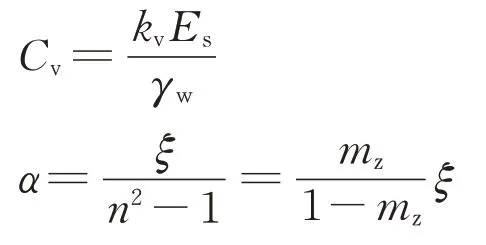
式中：Cv为天然土体的竖向固结系数，cm2·s-1。

由式（7）可以看出，刚性桩—筏复合地基由于桩的存在，使得其等价固结系数增大，且增大系数与置换率、桩—土压缩模量比密切相关。显然，同等条件下，刚性桩—筏复合地基的固结速率大于天然地基。

高速铁路工程实践多采用正方形式布桩，置换率极小，取值范围一般为4%～6%［7］，则

将式（8）代入式（6），进一步简化得到刚性桩—筏复合地基的固结微分方程为

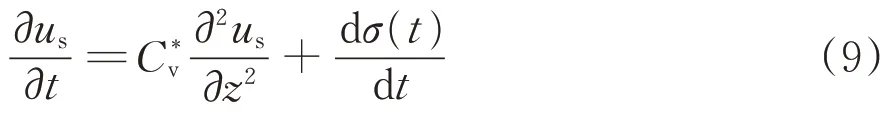
2 桩—筏复合地基固结方程求解

2.1 固结方程与求解条件

由式（9）可知，桩—筏复合地基固结微分方程为

其中，

求解条件如下。

（1）顶面边界：us|z=0=0（顶面排水）；

（3）初始条件：us|t=0=σ(0)，σ(0)为初始时刻t=0的地基附加应力。

2.2 孔隙水压力求解

参考太沙基单层地基一维固结理论，可设超静孔隙水压力为

式中：λi，βi，Bi和Ci均为待定系数。

Bi由初始时刻超静孔压us|t=0引起，根据求解条件（3）（初始条件us|t=0=σ(0)=0），可得Bi=0。Ti（t）为关于固结时间t的待定函数，由L（t）项引起。显然式（11）直接满足求解条件（1）顶面边界条件。

将求解条件（2）底面边界条件代入式（11）可得

将式（12）代入等效固结微分方程式（10），可得

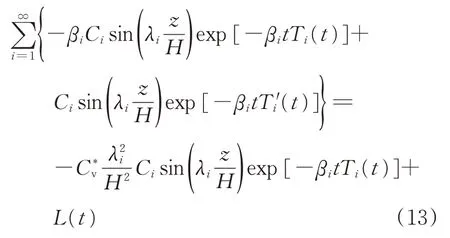
根据式（13）中的等式两边同类项相等，可得式（14）和式（15）。

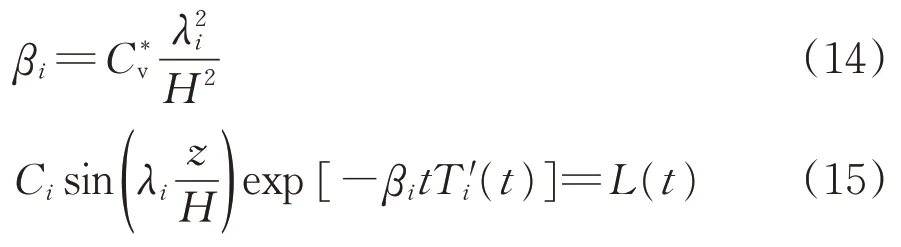
式（15）中待定函数Ti（t）和Ci应满足

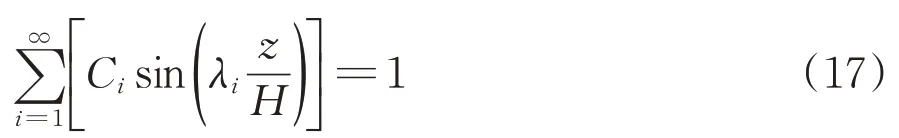
由此，可以写出满足所有求解条件（1）—条件（3）的超静孔隙水压力的一般解为

2.3 地基固结度求解

地基的平均固结度有2 种定义方式，第1 种按“沉降”或“变形”定义，即地基任一时刻的沉降量（变形量）与其最终值之比；第2 种按平均有效应力或所消散的平均超静孔压定义，即地基中任一时刻的平均有效应力（或所消散的平均超静孔压）与其最终值之比。而对于本文单层均质地基而言，2种定义下的平均固结度概念相同，其结果亦相同。

由于高速铁路路基工程更加关注“工后沉降”，故只计算按“沉降”定义的地基整体平均固结度U，即地基任一时刻沉降量（变形量）与最终值之比，得到端承型刚性桩—筏地基平均固结度U计算式，即

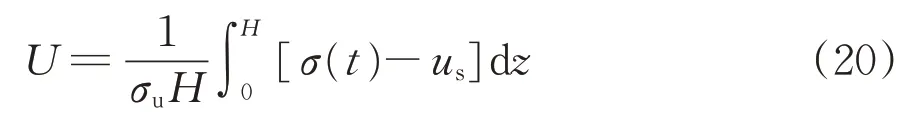
由超静孔隙水压力一般解式（19）和按沉降定义的平均固结度计算式（20），可得地基附加应力随时间任意变化情况下端承型刚性桩—筏地基平均固结度计算式。为节省篇幅，仅给出常见情况（荷载单级等速施加）计算式。

如图3 所示的单级等速加荷工况下σ（t）和L（t）可表达为

代入式（19）和式（20）可得加荷阶段和停荷阶段的超静孔隙水压力和平均固结度。

加荷阶段（0≤t≤tc）复合地基内超静孔隙水压力和整体平均固结度分别为

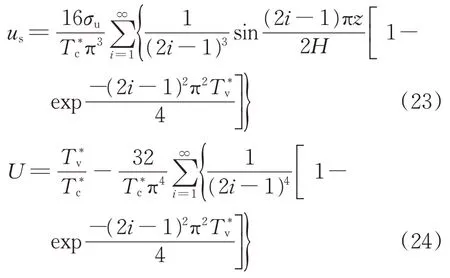
其中，

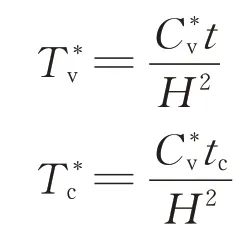
停荷阶段（tc＜t）复合地基内超静孔隙水压力和整体平均固结度分别为

2.4 合理性论证

为验证上文解析解的合理性，将其计算结果分别与文献［14］解析解计算结果和数值结果进行对比。数值模拟中主要对由刚性桩和其所加固的桩间土组合成的复合单元体进行固结分析，桩与桩间土均采用线弹性本构模型。数值模型如图4所示，相关参数设置如下：复合单元体总厚度10 m，长宽各为4 m；桩压缩模量150 MPa，桩泊松比0.3；桩长10 m，桩间距0.66 m，桩径0.15 m，置换率0.04；桩间土压缩模量3 MPa，桩—土压缩模量比50；渗透系数2×10-8m·s-1；单元类型为C3D8R。边界条件为：地基顶面为透水边界，地基底面为不透水边界。取复合单元体右侧表面沉降最大处为沉降计算点。上部荷载施加方式：单级等速施加载σu=100 kPa，tc=50 d。

图4 数值模型图

图5 和图6 分别为不同方法得到的桩—筏复合地基超静孔压和固结度的对比曲线。

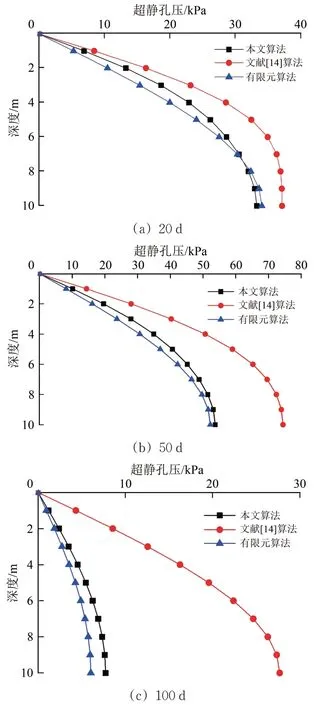
图5 复合地基超静孔压计算结果对比

图6 复合地基固结度计算结果对比

由图5 和图6 可知：本文方法与有限元方法结果更为接近，均小于文献［14］方法结果。本文方法考虑桩体置换作用和应力集中效应，得到的桩间土的固结系数约为原天然土体固结系数的3.08 倍，而文献［14］方法中将桩体与桩间土概化为均质复合土，得到的“复合土”固结系数约为原天然土体固结系数1.83 倍，显然本文方法得到复合地基固结速率要比文献［14］快（快出超过1 倍）。本文方法与数值模拟结果仍有一定差距，可将原因归结于未考虑排水路径长度不同对超静孔压消散速率的影响。

3 固结特性

3.1 工程背景

沪宁城际铁路（上海—南京）于2010年7月1日正式通车，设计速度350 km·h-1，全线采用无砟轨道。正线全长300 209 m，路基占线路全长的34.66%。线路穿越大量软土地层，采用多达7 种以上软基处治方式。为探索软土地基处治关键技术，针对不同地基处治措施在镇江段开展现场试验。其中，DK80+835 断面采用CFG 桩—筏复合地基处治，桩贯穿软土层刺入坚硬的持力层。DK80+835 断面设计参数：桩长8 m，即加固区深度8 m；桩径0.5 m，桩间距1.8 m；桩间土的平均压缩模量为7.168 MPa；桩间土的平均竖向渗透系数为2.46×10-9m·s-1；荷载施加条件假定为单级等速加荷，σu=100 kPa，tc=50 d。

3.2 置换率对固结速率的影响

图7为桩—土压缩模量比为139.51时，不同置换率下复合地基固结度随时间变化曲线。其中，mz=0 代表未经过加固处理的天然地基。地基固结速率可用同一时刻的固结度表征，同一时刻固结度越大，地基固结速率越快。

图7 不同置换率下固结度时变曲线

由图7 可知：加载完成时，天然地基固结度仅为26.06%，而桩—筏复合地基固结度为45.64%～71.95%；停荷后t=200 d 时，天然地基固结度仅为70.83%，而桩—筏复合地基固结度为96.6%～99.99%。无论加荷阶段还是停荷阶段，桩—筏复合地基固结度均大于天然地基，且差距随置换率的增大而增大；置换率从0增至0.03，同一时刻地基固结度增长明显，而从0.03 增至0.06，地基固结度的增长变得越来越缓慢，说明置换率适宜范围为0.03～0.06。

3.3 桩土压缩模量比对固结速率的影响

图8为置换率mz=0.04时，不同桩—土压缩模量比ζ下复合地基固结度随时间的变化曲线。其中，桩—土压缩模量比ζ=0 代表未经过加固处理的天然地基。

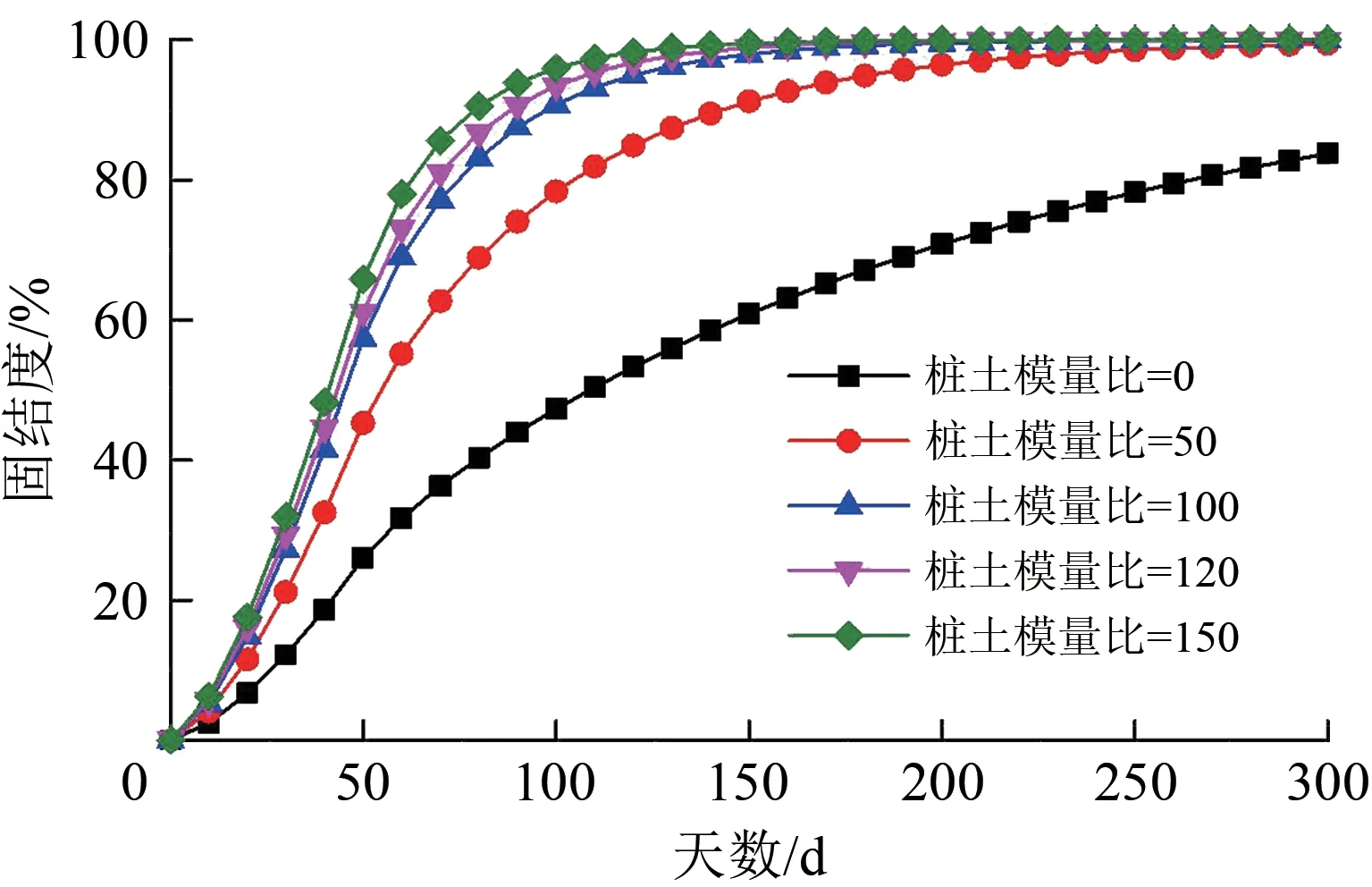
图8 不同桩土压缩模量比时固结度时变曲线

由图8 可知：刚性桩—筏复合地基的固结度随桩土压缩模量比的增大而变大；桩土压缩模量比从0 增至100，同一时刻地基固结度随模量比增大而增长明显，而桩土压缩模量比从100 增至150，地基固结度几乎不再增长。因此，桩土压缩模量比的适宜范围为100～150。

3.4 加荷速率对固结速率的影响

图9为桩—土压缩模量比为139.51，置换率为0.04 时，不同加荷速率下复合地基固结度随时间的变化曲线。σu保持不变，tc越小表示加荷速率越大。

图9 不同加荷天数时固结度时变曲线

由图9 可知：刚性桩—筏复合地基固结速率与加荷速率有关，tc从100 d 降至25 d 过程中，复合地基固结速率提升十分显著，表明加荷速率越大，复合地基固结越快。说明要想加快端承型刚性桩—筏复合地基的固结过程，增大加荷速率也是一种有效途径，即加快地基上部填土的填筑速率。

3.5 固结度计算实例

图10 为DK80+835 断面固结度随时间变化曲线。其中测试换算法为测试沉降数据与最终沉降比值，而最终沉降量为用现场测试数据采用文献［15］动态神经网络方法预测获取。

图10 DK80+835断面实测固结度和沉降

由图10 可知：本文方法获取固结度与采用实测沉降换算固结度基本吻合，说明本文方法的可靠性。

4 结 论

（1）因桩的置换作用和应力集中效应，端承型刚性桩—筏复合地基桩间土的等价固结系数增大，即相同条件下端承型刚性桩—筏复合地基固结速率大于天然地基。

（2）端承型刚性桩—筏复合地基固结速率随置换率、桩土压缩模量比、加荷速率的增加而逐渐加快；对沪宁城际高铁CFG 桩—筏复合地基分析表明，置换率和桩土压缩模量比的适宜范围分别为0.03～0.06和100～150。

（3）采用本文方法得到的固结度与实测沉降换算结果吻合，验证该方法的可靠性，可为类似工程沉降计算提供一种新的思路。