基于面板混合Logit模型的中长途高速客运方式分担率预测

盛冬冬,孙明妹

(北京交通大学 轨道交通控制与安全国家重点实验室，北京 100044)

目前，我国的高铁(high-speed railway, HSR)发展迅速，截至2019年底，高铁里程达到3.5万公里。高铁的迅猛发展极大地提高了铁路在中长途高速客运(即出行距离在800～1200 km的旅客运输)中的竞争力。高铁和民航(civil aviation,CA)的方式分担率模型是其竞争网络研究、定价研究等的重要基础，因此，对方式分担率模型的研究很有必要。

对方式分担率的模拟以离散选择模型为主，一般通过构建效用函数，使用个体数据对效用函数中的未知参数进行估计，继而计算出选择项被选中的概率。传统Logit模型是离散选择模型的基础模型，但传统Logit模型本身存在的IIA特性会对模型的预测结果产生很大的影响。何宇强等[1]、Hensher[2]、叶玉玲等[3]选择经济、快速、方便、舒适、安全5个指标建立传统Logit模型，并使用该模型对方式分担率进行预测。为了解决传统Logit模型中存在IIA特性问题，又提出嵌套Logit(Nested Logit, NL)模型。NL模型将相近的备选方案列入同一子集，子集内部仍存在IIA特性，但子集间的IIA特性不复存在。Adler等[4]和Wen等[5]分别建立NL模型，并使用数据对参数进行估计。然而传统Logit模型和NL模型都忽略了个体异质性，且没有完全解决IIA特性，混合Logit(Mixed Logit, ML)模型的出现，解决了上述两个问题。常见的混合Logit模型指的是考虑了个体异质性的横截面混合Logit模型(Cross-Sectional Mixed Logit, CML)，可使用横截面数据对其参数进行估计。Abdel-Aty等[6]使用具有正态分布的CML模型刻画在交通信息诱导下驾驶员对于路线选择的问题，得出旅行时间及其变化等因素会对路线选择产生影响。Li等[7]在北京地铁系统中进行了意向调查(stated preference, SP)，建立了考虑价格内生性的出发时间选择CML模型，得出票价和发车时间的变化对乘客出发时间选择的影响大于拥挤程度的结论。Behrens等[8]使用伦敦—巴黎客运市场的横截面数据估计了CML模型，结果表明，出行时间和频率是出行行为的主要决定因素。不同于CML模型，面板混合Logit模型(Panel Mixed Logit, PML)使用面板数据估计其参数，不仅考虑了个体异质性，同时也考虑了同源数据的相关性。车国鹏[9]通过建立PML模型，研究拥挤收费对城市交通方式分担率的影响。Guo等[10]使用沈阳的居民调查数据建立了PML模型，捕捉居民的交通方式选择的个体异质性。Chen等[11]使用PML模型研究了驾驶环境对碰撞频率的影响。

针对方式分担率的研究以传统Logit模型和NL模型为主，考虑到数据的收集难度，一般又以SP数据对参数进行估计，但很少有文献考虑到选择个体的异质性以及SP数据中同一数据源间的相关性。本文针对高铁和民航的方式分担率问题，建立了传统Logit模型、考虑个体异质性的CML模型和考虑个体异质性及同源数据间相关性的PML模型，使用北京—南京客运通道的SP数据进行参数估计，通过对比参数估计结果，发现PML模型具有更好的行为解释能力和预测精度。最后，在PML模型的基础上，利用仿真分析预测了高铁和民航的方式分担率随旅程费用差(民航与高铁票价差)和时间差(高铁与民航旅程时间差)的变化趋势。该结果能够指导运营商合理地调整票价和旅程时间，以在竞争中取得优势。

1 PML模型

1.1 ML模型阐述

ML模型是非常灵活的模型，可以近似成所有随机效用模型[12-13]，其参数可以指定服从某种分布，突出不同个体的选择偏好。

假设在情景k(k=1,2,…,K)下，个体i(i=1,2,…,I)面临选择j(j=1,2,…,J)时，i在考虑了所有备选方案后会选择效用最大的方案。一般形式的效用表达式如下：

(1)

式中，Uijk指i在情景k下选择j的效用；xijk指与方案j有关的特性变量组成的向量；β′和εijk指无法观测的随机影响，εijk服从同一Gambel分布，备选方案间不存在相关性。解决方法是通过β′将备选方案间异方差和相关性的随机元素引入效用函数，如式(2)所示(首先以横截面数据集为例，因此忽略k下标)：

β′=βij+ηij，

(2)

式中，βij为非随机参数；ηij是随机参数，表示效用函数集中除εijk外的随机影响的向量，随选择而变化，可能会引起备选方案间的相关性，可以指定分布，常见的有正态、对数正态、均匀分布等。

使用f(η|θ)来表示其概率密度函数，给定η值，选择j的条件概率为

(3)

但η的值并不知道，不能以η为已知条件得到条件概率，故，非条件概率应求解Lij(η)在所有可能的η值上的积分。

(4)

由式(4)得知，ML模型的选择概率可看作为多项Logit模型概率的加权平均值，f(η|θ)决定权重，θ是描述f(η|θ)的参数，以正态分布为例，θ指均值和标准差。

1.2 PML模型

常见的数据结构为横截面数据，其最大的特点是数据收集中存在的时间或情景差别很小。而面板数据是由数据集中每一个横截面单位的一个时间序列组成，这里的时间序列可以是不同时间也可以是不同情景。PML模型可以捕捉到不同情景下同一个体观测间可能存在的相关性。

决策者在情景k(k=1,2,…,K)序列下的选择条件概率为式(5)，PML模型的非条件选择概率同公式(4)。

(5)

1.3 参数估计

仿真的方法特别适合用于估计ML模型的参数，指定分布，其仿真概率如式(6)所示：①给定θ，从f(η|θ)抽取一个η值，记为ηr，表示第r次抽取；②计算Lij(ηr)；③重复①②步骤R次(R足够大)，将均值作为Lij(ηr)的仿真值。

(6)

求出使LL(η)得到最大值的θ。

2 问卷设计

本文将用到旅客各种情境下的选择数据，故SP方法更加适合。问卷内容包括受访者的基本信息、中长途出行特性及出行情景的方式选择意向。受控的动态变化试验因子包括高铁和民航的程前程后费用和时间以及旅程费用和时间4个变量。

假想的出行情景如图1所示，每种方式的费用和时间都是由程前(即出发地A至高铁站A高铁或机场A机场)费用和时间、旅程费用和时间、程后(即高铁站B高铁或机场B机场至目的地B)费用和时间组成。

图1 假想出行情景

借鉴已有研究[14]：出行距离在800～1200 km时，高铁和民航的竞争最激烈。故选择北京—南京客运通道作为研究对象。问卷使用正交试验法，试验因子设置为四因素三水平，参考文献[15]、12306官网及北京—南京航班信息，确定高铁和民航的旅程费用和时间的高、中、低三水平。依据L9(34)正交表设计了9种情景，如表1所示。该设计在保证数据可靠性和有效性的基础上，节省了大量人力物力。

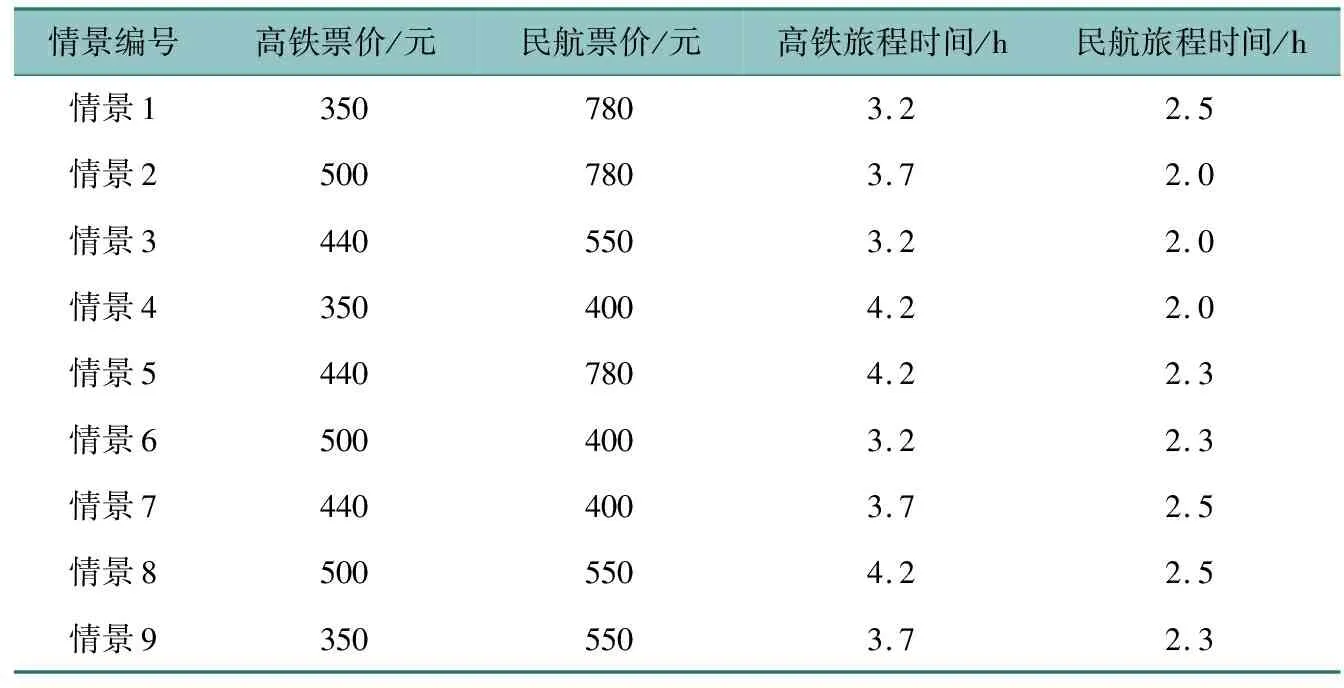
表1 情景设置

本次调查共回收问卷221份，有效问卷202份，合格率达91.4%，能有效地应用于后续的建模与分析。

3 数据分析与建模

3.1 统计分析

问卷中基本信息及中长途的出行特性分析结果如表2和图2所示。受访对象中男性占52%，女性占48%；年龄分布主要集中在(24，49]岁；月收入分布以[4000，10 000)元居多，占53%；出行目的以公务出行居多，占43%。而出行特性方面，高铁的程前程后平均时间1.6 h，民航的程前程后平均时间2.2 h；高铁的程前程后平均费用为35元，民航的程前程后平均费用为72元，该分布特征与实际情况基本相符。

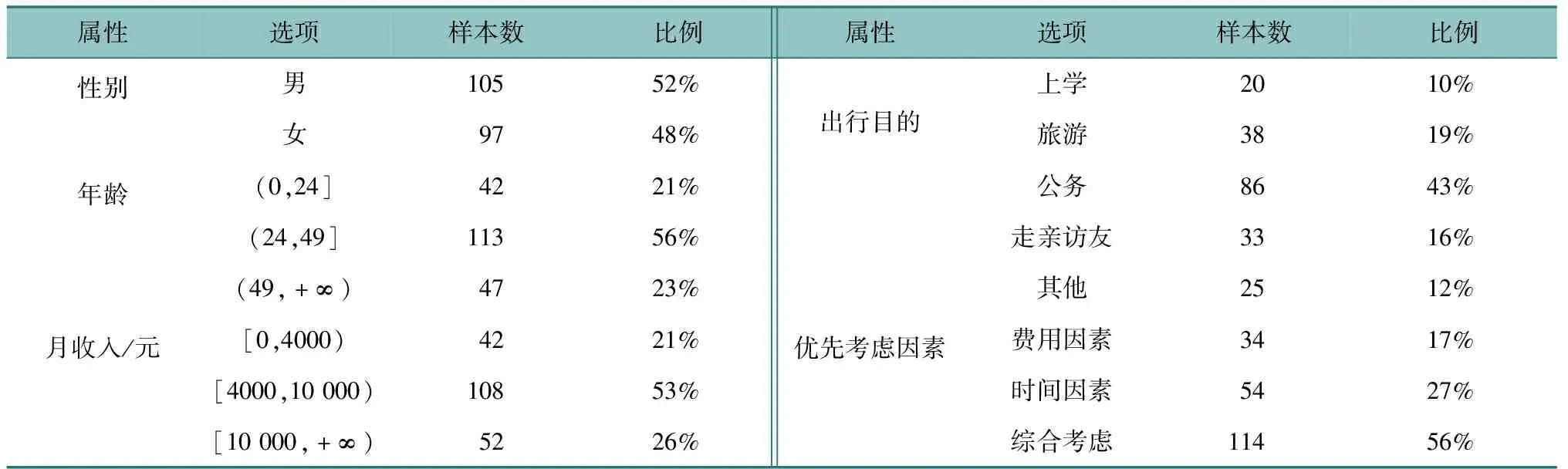
表2 问卷基本属性统计

(a)程前程后时间分布 (b)程前程后费用分布

3.2 模型构建

使用PML模型对样本数据进行建模，选择性别、年龄、月收入、出行目的、优先考虑因素、程前程后时间和费用、旅程费用和时间作为模式选择的特性变量，变量设置参见表3。根据上述变量描述，个体i选择j的效用函数可以表示为(以高铁作为参考)：

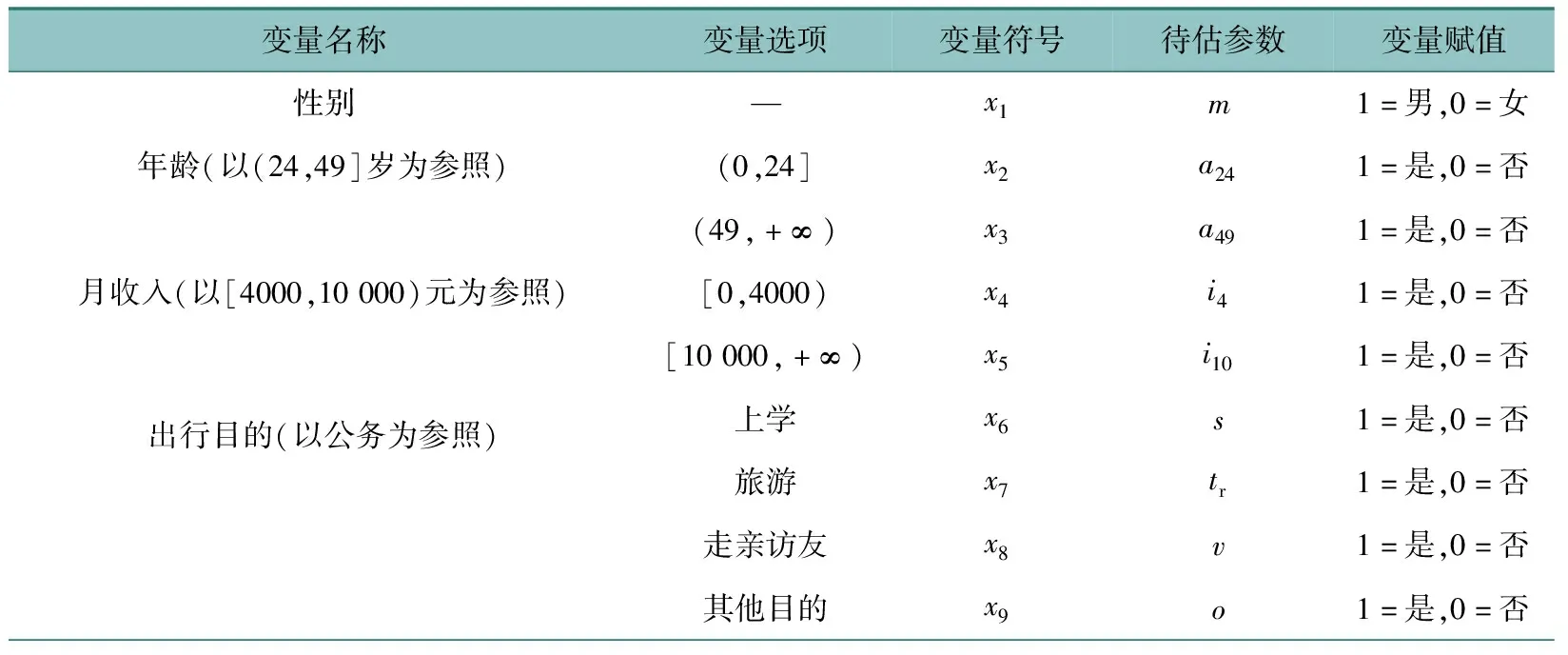
表3 特性变量表

UCA=Con+mx1+a24x2+a49x3+i4x4+i10x5+sx6+trx7+vx8+ox9+csx10+bx11+txt_s2+ctxt_ts2+fxp2+jtxt2，

(7)

UHSR=txt_s1+ctxt_ts1+fxp1+jtxt1，

(8)

式中，UCA表示民航效用函数；UHSR表示高铁效用函数；xp2、xp1分别指民航和高铁的旅程费用。xt_s2、xt_s1、xt_ts2、xt_ts1、xt2、xt1以此类推。

在建模过程中，通过仿真方法计算蒙特卡洛积分，该计算涉及到“伪随机序列”生成，选择了Halton法完成η的抽取，相较于标准伪随机序列法，极大地提升收敛性。接着，把数据整理成长型数据，导入NLOGIT，编写程序，对参数进行估计。

利用NLOGIT对1818(202×9)条有效数据进行建模。首先确定性别、年龄、月收入、出行目的、优先考虑因素为常系数，而两种交通方式的程前程后时间和费用、旅程费用和时间这4个变量具体的值也不同，要捕获个体异质性，就需要在这些变量中选取某些变量的系数作为随机系数。因此对这些变量进行了许多组合，在此基础上进行参数估计，并且对参数估计结果进行了评估，在这些组合中，有许多的组合参数估计结果违反了实际情况，多数参数的显著性检测无法达到95%的置信水平。在符合实际情况和显著性检测达标的组合中，通过比较麦克法登似然率来判断模型对出行选择行为的解释能力，最终将程前程后时间和费用、旅程费用和时间这4个特性变量的系数指定为随机系数并且服从正态分布。

3.3 参数估计结果

本文建立了传统Logit模型、CML模型及PML模型，使用SP数据进行参数估计，结果如表4所示，经对比，可以更全面地考察PML模型的效果。

由表4得，传统Logit模型、CML模型和PML模型的参数估计结果符号基本一致，这说明考虑了个体异质性和同源数据相关性后并未改变特性变量对方式选择影响的正负效应。3个模型的似然函数值分别为-801.153 0、-676.129 2和-532.525 6，通过该值可以计算出对应的麦克法登似然率。可以发现，传统Logit模型的麦克法登似然率为0.364 2，拟合优度不算高。考虑异质性后的CML模型的麦克法登似然率为0.463 4，说明CML模型相较传统Logit模型更适合模式选择行为的建模分析。而考虑了个体异质性和同源数据相关性的PML模型的麦克法登似然率为0.577 4，高于传统Logit模型和CML模型，说明PML模型具有更好的行为解释能力，拟合优度更高，在该数据集下的预测能力更好。

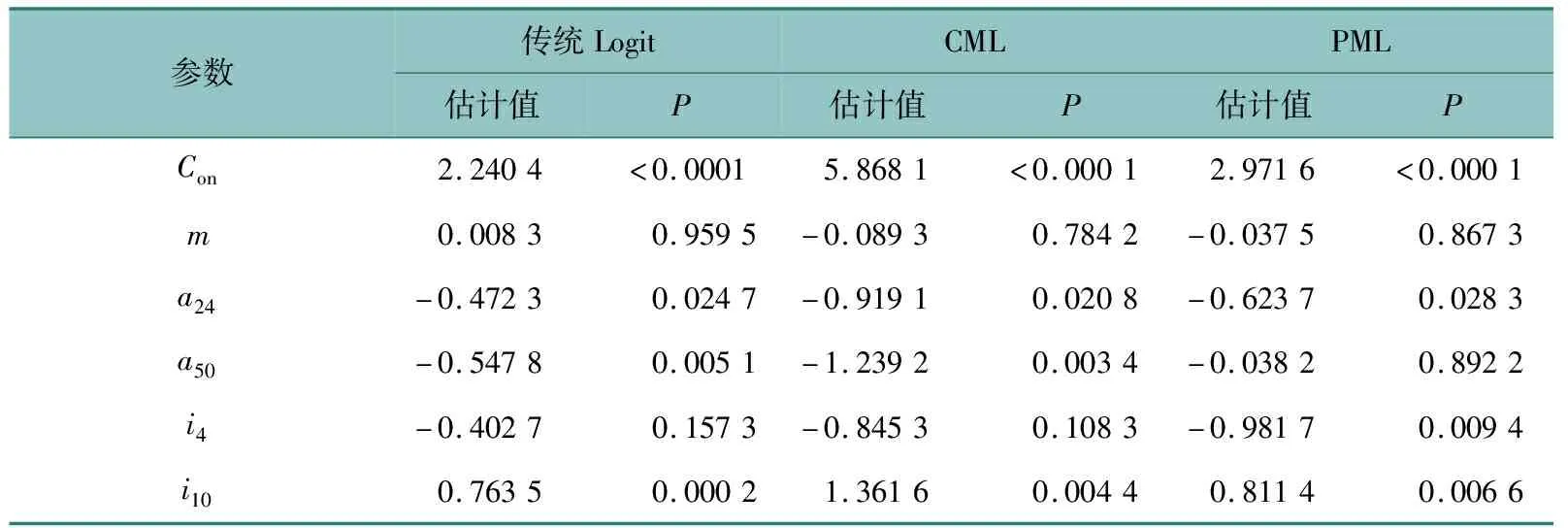
表4 参数估计结果

3.4 PML结果分析

由表4所示，所有参数的符号均符合逻辑。在95%的置信水平下，除性别、年龄(49，+∞)、优先考虑因素(时间因素)外，其他特性变量均显著。在95%置信水平下，年龄在(0，24]的个体符号为负，说明了相较于(24，49]岁的中青年，年龄在(0，24]的个体更倾向选择高铁出行；月收入[0，4000)元的个体较月收入[4000，10 000)元的个体更不愿意选择民航出行，月收入在[10 000,+∞)元以上的个体更愿意选择民航出行；而以上学、旅游、走亲访友和其他为目的的出行者较公务出行者更倾向选择高铁出行；时间主导者或时间费用主导者较费用主导者更倾向选择民航出行。其中随机参数均在99%的置信水平下显著，即t～N(-2.845 7,0.665 2)、ct～N(-0.029 5,0.010 1)、f～N(-0.021 8,0.009 7)、jt～N(-1.827 3,0.338 9)，而程前程后时间和旅程时间的标准差相对较大，说明了不同个体对时间的敏感程度有较大的差异，异质性明显，并且4个随机参数在两个标准差范围内符号均为负，说明了程前程后时间和费用及旅程费用和时间越大，这种交通工具被选择的概率越低，这符合实际情况。

使用参数估计得到的结果对原始数据的选择进行仿真，得出基于PML模型的两种交通方式的选择概率，选择概率大的作为模型的预测结果，通过与实际选择结果对比，得出模型的准确率，部分结果如表5所示。表中ID指受访者的序号，相同的序号表示数据来源于同一受访者经仿真结果统计；选择栏为受访者的实际选择。PML模型的准确率达85.37%，其中，高铁的准确率为88.58%，民航的准确率为81.38%，模型拟合效果良好，具有较高的预测精度。

表5 部分仿真结果

4 模型应用

为进一步研究旅程费用和时间对中长途高速客运方式分担率的影响，使用PML模型仿真分析在不同旅程费用差和时间差下的方式分担率。采用集计预测中的样本枚举法[16]进行预测，如式(9)所示，该方法是把总体中的一个随机样本作为 “代表”，样本中选择某一选项的比例作为总体中选择该选项的一个无偏估计。使用NLOGIT软件中的simulation功能，在SP数据的基础上，不改变性别、年龄等基本属性，改变旅程费用差和时间差得出个体的选择概率后，使用式(9)得出该总体的估计值。

(9)

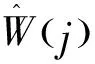
方式分担率随旅程费用差和旅程时间差的变化趋势如图3所示，图中红线部分为高铁方式分担率与民航方式分担率相等的情况。由图3可以得到，高铁的方式分担率随着旅程费用差的增大而提升，随着旅程时间差的增大而降低，且在高铁和民航方式分担率相同时，旅程费用差对高铁分担率的影响比旅行时间差要更加显著。高铁和民航方式分担率相同时，伴随着旅行时间差的缩小，旅程费用差由最初的150元降低到40元。当高铁和民航的旅程费用差和时间差在红线周围时，二者的竞争最为激烈。以旅程时间差达到2 h为例，旅程费用差超过110元时，高铁和民航的竞争中，高铁处于优势地位，且旅程费用差在[110，280]元区间时，高铁方式分担率的提升速率最快。

图3 方式分担率仿真结果

5 结论

本文针对高铁和民航的方式分担率问题，建立了传统Logit、CML和PML模型，使用旅客SP数据对模型参数进行估计，通过对比参数估计结果，得出PML模型较传统Logit和CML模型，具有更好的行为解释能力和更高的预测精度。PML模型的估计结果说明，个体对时间因素的敏感度有比较大的差异，个体异质性明显，且随机参数在两个标准差范围内符号均为负，说明程前程后时间和费用及旅程费用和时间越大，该交通工具被选择的概率越小。在基于PML模型的仿真分析中，得到高铁的方式分担率随旅程费用差的增大而增加，随时间差的增大而减小，民航恰好相反，且旅程费用差对方式分担率的影响比旅程时间差更加显著。仿真分析结果能有效指导运营商改变票价和旅程时间，以在竞争中取得优势。此外，PML模型可以在交通规划、交通方式竞争等研究中广泛使用。

本文问卷的正交设计虽节省了人力物力，但限制了数据的全面性，且收集到的SP数据量不够充足，会对模型参数估计结果产生影响。此外，为了简化模型，未将安全性、舒适性、方便性等影响因素纳入模型中，这些问题都是继续完善PML模型的主要方向。