含缺口PBX 药柱热冲击响应的数值模拟及试验

2021-02-03唐明峰甘海啸温茂萍王胜男

含能材料 2021年1期

唐明峰，甘海啸，温茂萍，王胜男

（1. 中国工程物理研究院研究生院，北京 100081；2. 中国工程物理研究院化工材料研究所，四川绵阳 621999）

1 引言

高聚物黏结炸药（polymer bonded explosive，PBX）是由单质炸药及高聚物黏结剂等组成的混合炸药。在贮存、运输、装配及使用过程中，PBX 可能受到温度循环、温度梯度、温度冲击等多种类型的温度载荷作用，其中温度剧烈变化形成的热冲击最容易使PBX结构产生损伤及破坏［1-3］。近年来，随着实战化要求的提高，优化抗热冲击性能已逐渐成为PBX 配方研究的重要发展方向。

在无机非金属材料中，通常将材料承受温度急剧变化而不致破坏的能力称为抗热冲击性，也称热稳定性或抗热震性［4］，它与材料力学性能和热物理性能密切相关，并受到边界约束、几何尺寸和温度条件的影响。作为一种低强度脆性材料，PBX（特别是压装PBX）对外界热冲击尤其敏感，很容易在热应力作用下出现损伤、断裂等影响炸药结构完整性的现象，提升环境适应性是新型PBX 研制的重要方向。如何在实验室条件下快速评价PBX 的抗热冲击性能，则是影响配方研制进度的关键因素［5］。一种方法是参照陶瓷等脆性材料［6-7］，利用材料基本物性开展热冲击阻力（thermal shock resisitance，TSR）的初步估算。这在PBX 配方研制初期是有用且必要的，可以较快的对不同配方PBX 的抗热冲击能力进行对比，王鹏飞［8］、林聪妹［9］及He［10-12］等均采用了类似方法。然而TSR 方法不能很好地处理PBX 力热性能的温度相关性，且真实PBX 成型件的形状因子难以确定，因此估算得到的临界断裂温度等数值存在较大偏差。另一种方法是通过试验来确定材料的抗热冲击能力，目前文献报道的炸药热冲击试验［13-16］可大致分为小药柱水浴淬冷法和大试件（或原型件）风冷降温法。田勇等［13-14］在PBX水浴淬冷法方面开展了较多的试验，该方法所需的材料用量小，测试简单，可在炸药配方研制初期进行快速横向对比，缺点是只能在试验前后分析性能变化及是否破坏，较难获得损伤破坏的定量过程信息；后者一般采用圆柱形试件或块状试件，可以通过粘贴各类传感器获得温度、应变、声发射等结构响应信息［15-16］，方便与有限元计算及理论分析的对比，难点在于试样构型设计，即试样需要尽可能小并能反映真实构型的热应力分布或特征，对强度及导热性能增强的材料还需要特殊的设计以使试样可在实验条件下破坏。

与其它脆性材料相比，目前PBX 抗热冲击性能研究还相对较少。一方面，PBX 材料性能的温度敏感性和装药结构上的特殊性限制了TSR 等理论方法的深入应用，从而难以实现真正意义上的炸药环境适应性设计；另一方面，缺乏标准的PBX 抗热冲击试样方法，包括面向材料研制的快速检测方法及面向工程的等效评价方法。其中，认识PBX 热冲击响应特性是关键。为此，本研究针对缺口圆柱这一特殊结构，以某HMX 基PBX 为对象，开展风冷快速降温条件下的热冲击响应研究，通过试验和数值模拟确定PBX 的温度、应变等响应特征，以及破坏条件和模式，以进一步认识PBX的环境适应性并发展炸药温度冲击试验方法。

2 数值模拟

材料性能恒定的无限长圆柱的温度冲击可视为一维非定常热传导问题，存在解析解。而PBX 的力学性能和热物理性能随温度变化而变化，且短圆柱构型和缺口等局部结构使之成为二维/三维问题，热传导和热应力变得复杂，有必要先通过数值模拟认识圆柱内部的温度、应力分布特征及缺口应力集中的影响。

2.1 材料模型

研究发现PBX 的力学性能和热物理性能均与温度相关。本研究采用热弹塑性假设，力学性能根据实测应力-应变关系（如图1所示）输入，热物理参数取自文献［17］，其中选用HMX基PBX，其密度1.845 g·cm-3，泊松比0.33。

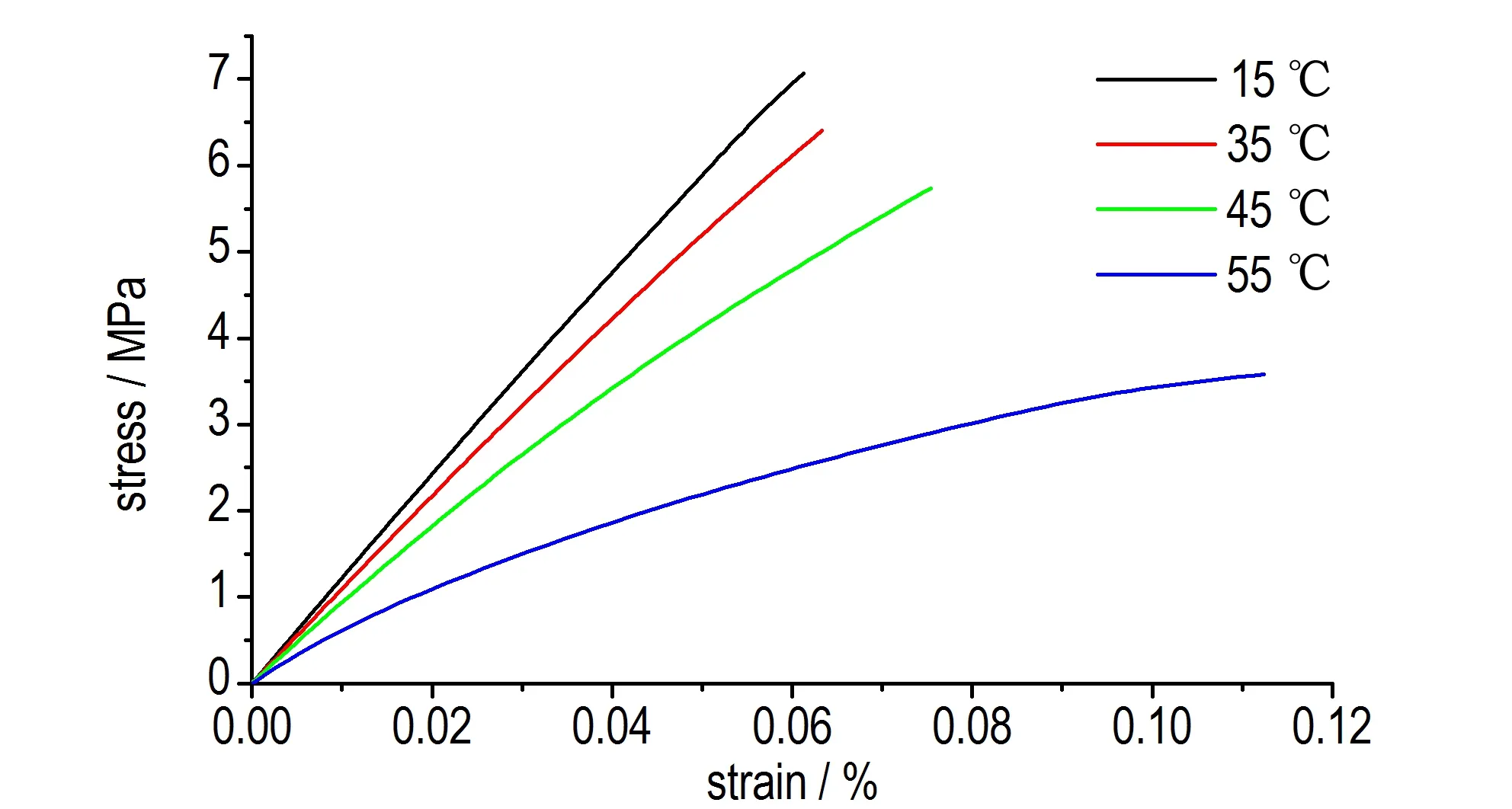
图1 不同温度下PBX 的拉伸性能Fig.1 Tension behavior of the PBX under different temperatures

2.2 几何模型

PBX 圆柱的轮廓尺寸为100 mm×110 mm，圆柱侧面分别含半径R0、R1、R2、R3及R4的圆形缺口。考虑结构和载荷对称性，取圆柱子午面建立1/4轴对称模型，网格划分按四结点轴对称热耦合四边形单元CAX4T，受热面10 mm 区域内网格尺寸约0.5 mm，圆柱内部网格尺寸约1 mm，单元总数约3900 个，如图2 所示。

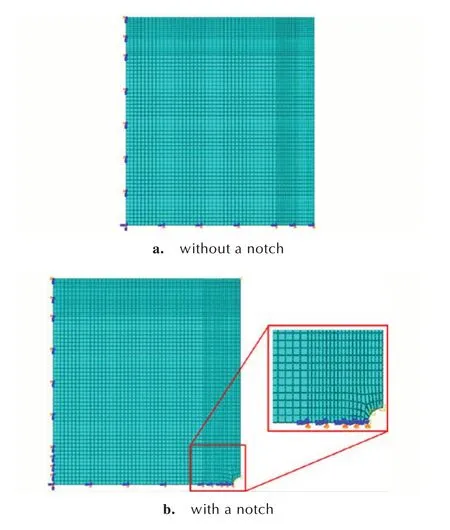
图2 PBX 热应力计算几何模型及网格划分Fig.2 Geometrical model for thermal stress calculation and its gridding division

2.3 边界条件

PBX药柱与周围空气靠强迫对流换热，风速约3 m·s-1，实测得到药柱表面对流换热系数为60 w·m-2·K-1。为形成显著的降温温度冲击，需要先将药柱缓慢升温一定温度，然后再进行快速降温，试验设计上需保证炸药在升温过程中不破坏且升降温全过程炸药性能没有突变。考虑到该炸药在50 ℃以上有明显的物性转变［18］，因此试验条件设定为：初始温度室温（20 ℃），按1 ℃·min-1升温至50 ℃并恒温3 h 后，再按10 ℃·min-1开始降温至0 ℃或至试样破坏。

2.4 无缺口药柱的热传导和热应力

图3 为PBX（Φ100 mm×110 mm）药柱热传导计算结果。图3a 为计算结束时刻1/4 圆柱面的温度场，其中A点位于外侧面中点，B点为圆柱中心。考虑半径方向（B→A），可见温度变化在离A点1/10 半径范围内最明显，即温度剧烈变化被限制在圆柱表面的薄层中，可看成一种温度边界层，而B点向外30 mm 内的温度基本保持在初始温度50 ℃不变。图3b 为升降温过程中点A、B的温度历史，两点间温度差在2115 s 附近达到最大值约18.7 ℃，在恒温阶段，两点间的温度差逐渐消除至零，降温开始后（约12600 s）A点温度急剧下降，药柱内外温差变为负值并持续减小，计算结束时刻A、B两点温度差达到-21.2 ℃。

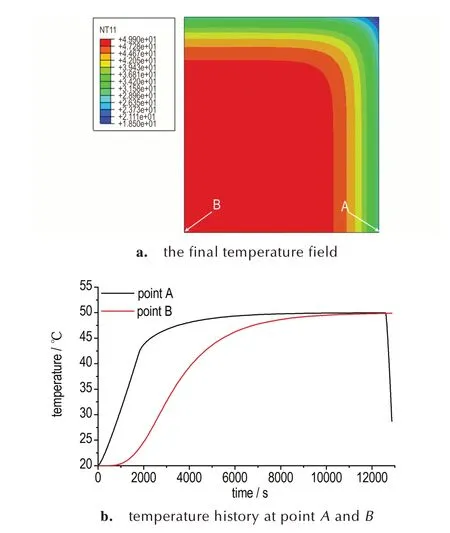
图3 无缺口药柱温度模拟结果Fig.3 The temperature simulation results of the PBX cylinder without a notch（Φ100 mm×110 mm）

仍考虑B→A半径方向。根据前述分析，试验过程中A、B两点的温差由正变负，根据热弹性理论，热应力方向与温度梯度方向相反，可知升温过程中B点承受拉应力，A点承受压应力，降温过程中则相反。图4 是该药柱热应力计算结果，图4a 给出了降温结束时药柱y方向的应力云图。图4b 为A、B两点y向热应力S22 随时间变化曲线。可见升温过程中B点最大拉应力为6.6 MPa，对应时刻2167 s，对应温度26 ℃，热应力小于此时PBX 的拉伸强度6.7 MPa，此时材料不会断裂；降温过程中A点拉应力急速升高，在12807 s时热应力达到6.9 MPa，已经超过此时PBX 的拉伸强度6.40 MPa（对应温度35 ℃），若以最大拉应力为判据，随着热应力继续增大，PBX 药柱将会发生断裂。因此后续分析主要以降温阶段的温度冲击为主。

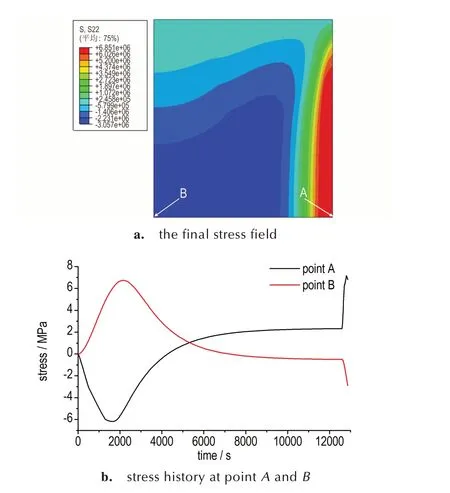
图4 无缺口药柱最大拉应力模拟结果Fig.4 The maximum tension stress simulation results of the PBX cylinder without a notch（Φ100 mm×110 mm）

2.5 缺口对药柱应力分布的影响

根据Φ100 mm×110 mm 药柱热传导和热应力分析结果，降温过程中PBX 药柱存在一个温度边界层，厚度约为半径的1/10，即5 mm，在该厚度范围内药柱的最大拉应力下降超过50%。圆柱外侧中心A点是温差和热应力较大的位置，容易因拉伸热应力破坏。若在此处预制半圆形缺口，热应力将因为应力集中效应而放大，使得相同尺寸下的断裂温度减小，或者可在保持断裂温差不变的情况下缩小试样尺寸。考虑温度边界层厚度，缺口深度宜小于5 mm。下面通过改变缺口的深度，研究其对药柱热应力大小和分布的影响。

仍采用Φ100 mm×110 mm 圆柱，保持外部温度条件不变，由于缺口会改变当地流速，进而影响表面换热，因此假设缺口中的边界换热条件包含对流换热和绝热两种情况，缺口半径设计为R1、R2、R3 和R4。计算结果表明4 种构型下药柱表面的热应力分布和变化规律一致。以R1 构型圆柱为例，图5 是对流换热条件下该药柱对称面上的热应力分布，与图4a 结果相比，A点（缺口底部）附近的应力梯度进一步增大，应力集中现象明显。在恒温过程中，由于塑性和应力集中，A点应力呈现拉伸状态；降温过程中A点S22 方向的拉伸热应力达到7.86 MPa，相比较于无缺口圆柱侧面最大拉应力6.90 MPa，增大了14%；最大主应力位于A点向内约0.67 mm 处，其值为10.76 MPa。类似地，可分别得到半径为R2～R4 时，缺口底部A点的热应力分别为7.79、7.75 MPa 和7.74 MPa，最大主应力分别为11.25、10.80、10.14 MPa，并分别位于A点向内约1.31、1.67 mm 及2.00 mm 处，如表1 所示。以相同条件下无缺口圆柱表面应力（6.90 MPa）为参考应力，可得到对流换热条件下四种缺口构型的应力集中系数分别为：1.56、1.63、1.57、1.50。同时，当缺口设为绝热边界时，计算结束时刻四种构型缺口底部位置的热应力分别为8.16、7.57、7.20 MPa 及6.93 MPa；最大应力分别为11.38、10.89、9.79、8.79 MPa，并分别位于A点向内约0.67、1.12、1.33 mm 及1.50 mm 处。计算得到应力集中系数分别为1.65、1.58、1.42 和1.27。结果如图6 所示。

图5 R1 缺口圆柱最大拉应力模拟结果Fig.5 The stress simulation results of the PBX cylinder with R1 notch

表1 不同缺口半径药柱的最大应力及位置Table 1 The maximum tension stress and location（distance from point A）of different notched cylinders

图6 药柱缺口处应力集中系数与缺口半径关系Fig.6 The stress concentration factor as a function of radius

2.6 缺口对药柱临界断裂温差的影响

在热传导和热应力分析的基础上，容易得到A点拉伸热应力与温度间的变化规律（图7）。图1 已知该PBX 在不同温度下的拉伸强度，可以据此确定PBX 药柱热冲击断裂的临界温差。观察到20～50 ℃范围PBX 材料的强度随着温度降低近似呈指数缓慢增长［18］，而在降温过程中，药柱表面拉应力以近似线性迅速增加，当二者数值相等时，PBX 药柱将发生热应力断裂（第一强度准则）。图7 给出了Φ100 mm×110 mm 无缺口药柱、R2 缺口药柱A点位置的热应力-温度以及PBX材料的强度-温度关系。无缺口时，两曲线在37.4 ℃相交，即药柱热冲击断裂临界温差为12.6 ℃；有缺口时（考虑热对流），两曲线在41.7 ℃相交，对应的热冲击断裂临界温差为8.3 ℃。由此可见，相同温度载荷下，PBX 药柱侧面缺口的存在将使试样可承受的临界断裂温差大幅降低，R2 缺口下的降低比率约为34%。

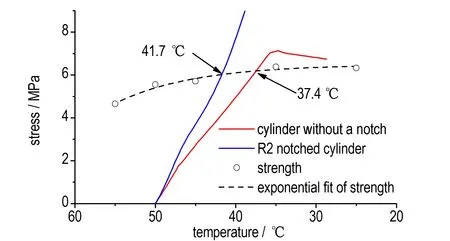
图7 热应力及材料强度变化趋势Fig.7 History of the simulated stress and tested strength for cylinders with and without a notch

3 实验验证

3.1 材料与试验

试验对象为前述数值模拟的某HMX 基PBX，试验在Espec快速温变环境试验箱（型号SEF-A-200UQS）中开展，试验条件与2.3节一致。采用Φ100 mm×110 mm药柱及带R2缺口Φ100 mm×110 mm 药柱，药柱A点位置粘贴热电偶、应变片以及声发射传感器用于结构响应信号监测，其中缺口药柱测点位于缺口边缘柱面。当PBX 药柱因热应力发生断裂时，将会释放弹性波并且使药柱应力分布重排，从而产生较强的声发射信号并使应变信号发生突变，据此可以确定试样断裂时间以及对应的温度。各传感器布置如图8所示，其中温度测量采用T型热电偶，由Fluke2680型温度巡检仪采集数据，采样频率1 Hz；应变监测采用带自补偿的三线制电阻应变片及HBM1615B 型应变采集仪，采样频率1 Hz；用Φ10 mm声发射探头采集声发射信号，采样频率为20 MHz，利用Vallen公司AMSY-6 AC采集。

图8 PBX 药柱表面的三种传感器布置照片1—声发射探头，2—热电偶，3—应变片Fig.8 Layout of three kinds of sensors on the PBX cylinder 1—AE sensor，2—thermocouple，3—strain gauge

3.2 实验结果

图9 是PBX（Φ100 mm×110 mm）药柱在温度冲击试验中测得的温度、应变、声发射响应信号。图9a给出了无缺口药柱在试验全过程的温度、应变历史，与前述数值模拟结果相比，发现试验和仿真得到的A点温度结果吻合很好，该点应变历史也符合压应力到拉应力的转变过程，破坏时的拉伸应变接近PBX 材料的断裂应变。图9a 右图是试样断裂前后的应变和声发射信号，数据分析发现在12280 s 附近，应变曲线出现了突跳，同时声发射探头接收到了接近100 dB 的信号，表明该时刻是药柱发生热冲击断裂的时刻。对比图9a 左图，可知12280 s 对应的A点温度为37.5 ℃，即试样的临界断裂温差为12.5 ℃，这与2.6 节计算得到的温差12.6 ℃十分接近。

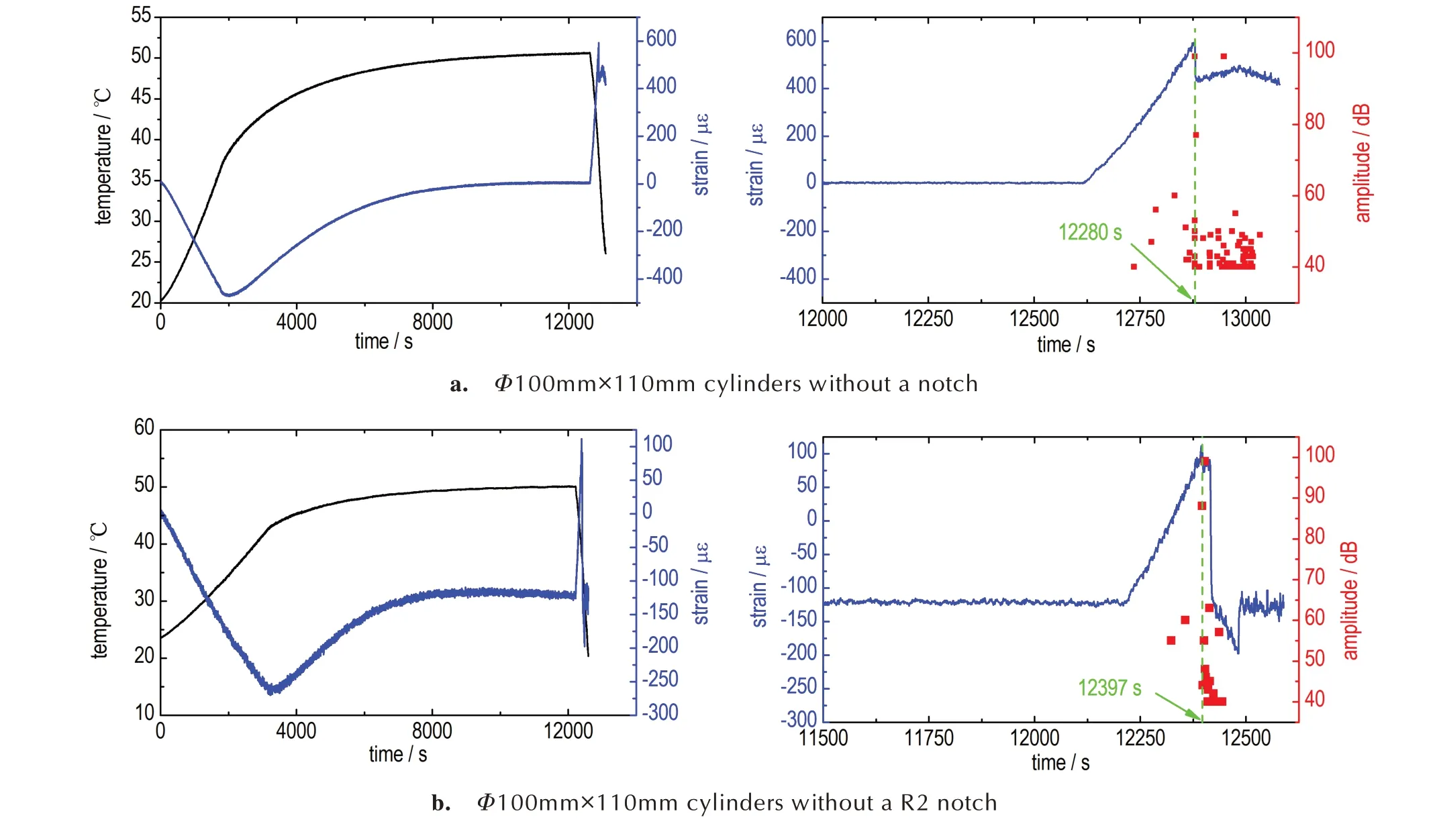
图9 药柱温度冲击试验的温度-应变-声发射监测信号Fig.9 Measurements of temperature，strain and AE signals on thermal shock experiments

图9b 是带R2 缺口的Φ100 mm×110 mm 药柱温度冲击过程中的信号监测结果。与无缺口药柱明显不同的是，缺口旁的应变片信号在恒温阶段没有回到零点，分析是由于缺口处的复杂应力形成的约束效应导致，如图9b 左图。药柱断裂前后的应变-时间及声发射幅值-时间如图9b 右图所示，易见12397 s 时应变信号发生了第一次突变，同时有高幅值声发射信号产生，说明药柱在该时刻发生了断裂。进一步，可得到12397 s 对应的试样缺口底部温度为40.8 ℃，即对应的断裂温差为9.2 ℃，与前述计算结果（8.3 ℃）相比误差为11%。分析认为一是由于缺口处的风速下降，导致实际表面换热系数降低，使得计算结果偏高；二是缺口处形成了更为明显的三维应力状态，使得图7 中第一强度准则的估算误差增大。该问题的优化还需要借助于炸药多轴强度准则的发展。

图10 温度冲击后PBX 药柱的破坏形貌Fig.10 Morphology of the PBX cylinders after thermal shock

图10 为PBX（Φ100 mm×110 mm）药柱及应力集中效应最为显著的R2 缺口药柱在破坏后的形貌。由图10 可见两种构型药柱均从侧面中部起裂，并形成贯穿性裂纹，裂纹平直无分叉，符合简单拉伸破坏特征，与前述热应力分析结果一致。从断面上看，破坏面较为光滑平坦，边缘无收缩，属于脆性断裂，可以很好地与图9 中药柱断裂现象对应，即应变急剧下降并且产生高幅值声发射信号。