斜波压缩下PBX-59 未反应固体炸药的状态方程

种 涛，蔡进涛，王桂吉

（中国工程物理研究院流体物理研究所，四川 绵阳 621999）

1 引言

爆轰过程的计算模型中，未反应固体炸药的完全物态方程对于描述高压和高温下未反应固体炸药的压力、温度等热力学状态参量的精度，直接关系到炸药化学反应率模型和炸药产物状态方程的计算精度。作为典型的多组分非均质颗粒材料，未反应固体炸药的完全物态方程构建依赖于宽压力区间内炸药的动力学实验数据。因此利用磁驱动斜波压缩加载实验技术开展固体炸药的动力学行为研究，其中一个重要的目的是获得0～20 GPa 压力范围内未反应炸药的状态方程参数，这是开展爆轰物理建模和安全性研究最基本的前提。

相比于冲击加载，斜波加载的重要特点是加载过程中样品的温升低，熵增小，因而有利于拓宽未反应固体炸药的加载压力范围，进行压力与温度分解的较高应变率动力学实验，得到关于材料高压相变动力学和炸药化学反应特性的新认识，进而可在宽压力范围内校核各种计算物理模型，使计算结果更加准确、可靠。自2000 年美国桑迪亚国家实验室（SNL）在Z 机器上建立磁驱动准等熵压缩加载实验技术以来，劳伦斯利弗莫尔国家实验室（LLNL）就有组织地对其武器用炸药型号进行了斜波压缩实验研究，后续的6 年时间里，对超过15 种炸药型号或样品进行了磁驱动准等熵压缩加载［1］，这其中还不包括SNL 开展的炸药准等熵压缩加载实验研究［2-5］。新的加载实验技术将未反应固体炸药宏观速度响应的压力范围拓展到20 GPa 以上，未反应固体炸药高压段实验数据缺乏的情况得到改善，补充了炸药响应数据库，对未反应炸药的状态方程有了更直观的认识，更有利于校核炸药的完全物态方程模型［6］，为爆轰模拟计算提供基础的物性参数。

中国工程物理研究院流体物理研究所自2006 年以来，积极发展磁驱动装置及斜波压缩加载实验技术［7-9］，实现了固体炸药的磁驱动斜波压缩加载实验技术及其数据处理方法［10-12］，拓宽了未反应固体炸药及组分动力学响应研究的压力范围（～20 GPa），改善了未反应固体炸药特别是国内配方炸药高压段实验数据缺乏的情况，为精密爆轰物理和炸药安全性研究提供了新的研究手段。

本课题组开展了18 GPa 压力下未反应固体炸药PBX-59 的动力学行为研究，从磁驱动斜波加载实验、数据处理与分析、数值模拟和基于实验结果的物态方程构建等四个方面，描述了利用磁驱动装置开展固体炸药动力学行为研究的过程。

2 固体炸药的磁驱动斜波压缩加载实验

PBX-59 炸药是以95%HMX 晶体颗粒、5%的黏结剂和钝感剂为组分的典型PBX 炸药，理论密度［12-13］1.889 g·cm-3，。本次实验样品PBX-59 炸药样品由中国工程物理研究院化工材料研究所提供，平均密度为1.848 g·cm-3，密实度为97.8%（密实度是炸药固体物质体积占总体积的比）。

在磁驱动装置CQ-4［14］上开展固体炸药的动力学行为实验研究。CQ-4 装置由6 个单元组成，分别为充电单元、储能单元、开关单元、传输单元、负载单元、能量泄放单元。装置最大峰值电流约4MA，电流上升沿500～800 ns。其中负载单元为条片式结构，用于上下对称地对样品材料进行动力学加载。磁驱动加载装置的负载区结构示意图如图1 所示，平行电极板之间用厚度约0.3 mm 厚的绝缘材料隔开。装置放电时由于趋肤效应，脉冲大电流流经样品对称安装的条形电极板内表面，产生压力平滑上升的洛伦兹力，洛伦兹力作用于电极板内表面，对“电极板-样品-窗口”三明治结构进行斜波压缩，利用激光干涉测速技术，如DLHV［15］（Dual Laser Heterodyne Velocimetry）测量不同厚度样品/窗口界面处的速度响应，处理数据获得样品材料的动力学参数。

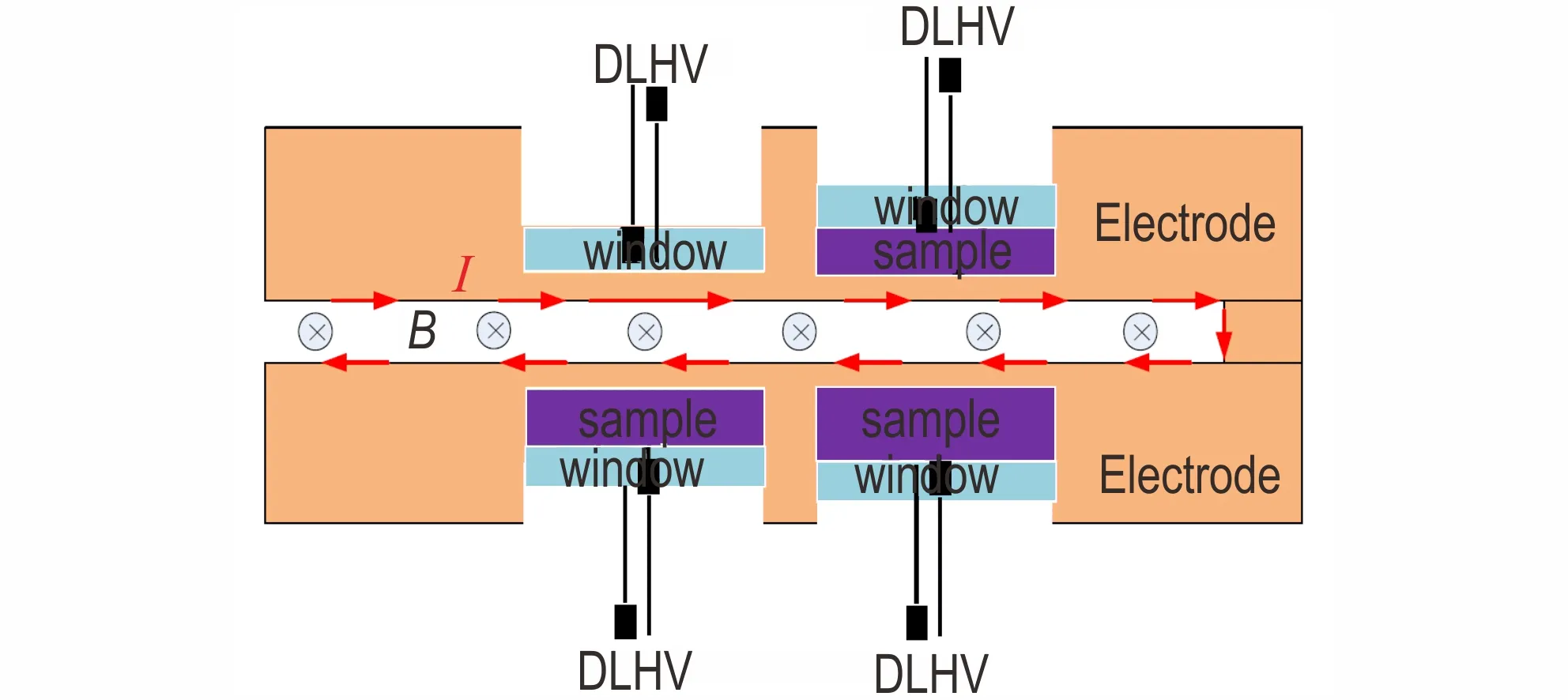
图1 负载区结构示意图Fig.1 Schematic of the loading area

实验用的驱动电极材料为纯铝，驱动电极板厚度1 mm。窗口材料为单晶LiF，厚度4 mm，单面镀铝反射膜，该面安装在样品后表面，用于激光干涉测速的反光面，由连续性条件知，铝膜处速度与样品后表面粒子速度一致。实验条件见表1，考虑了4 种不同加载电压下炸药样品的速度响应。每发实验安装3 种厚度的炸药样品，样品直径都是10 mm，在第四个位置安装LiF窗口，以求解实验加载压力历史波形。

实验获得了4 发实验的速度响应曲线，见图2。由图得，同一发实验中，随着样品厚度的增加，实验获得的样品与窗口界面处的速度曲线陡度增加，部分厚样品材料中形成了冲击波。由公式（1）知，斜波加载下，后续压缩波相对于前驱压缩波是超声速，当样品厚度足够，后续压缩波将追赶上前驱压缩波，并在样品中一定厚度处出现冲击波，在样品后表面（样品与窗口界面）处可观测到冲击剖面。加载峰值压力越高，样品中形成冲击的临界厚度越薄。当形成的冲击波幅值足够大时，极可能引起炸药发生化学反应，并在速度幅值上出现增量。

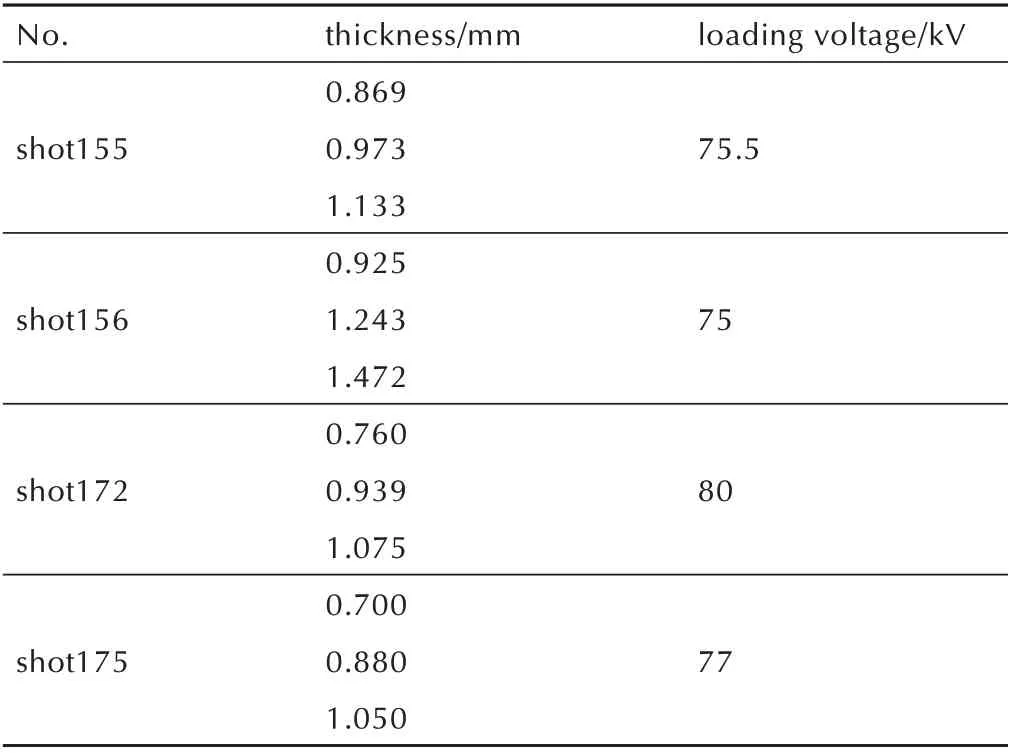
表1 斜波压缩实验条件Table 1 Experimental conditions of ramp wave loading

式中，cL是材料的纵波声速，c0和s为材料属性相关的动力学参数，up是材料的粒子速度。其中cL、c0和up单位是m·s-1，s是无单位参数

铝与LiF 窗口的波阻抗较为接近，忽略铝和LiF 窗口的阻抗差异，利用铝/LiF 界面速度曲线，可以得到界面压力，忽略Al 电极中的烧蚀和磁扩散效应，认为Al电极中波的传播为简单波，对上述界面压力作时间上的反演修正，可得到铝电极内表面的压力历史曲线。当对Al 和LiF 之间的速度曲线进行波阻抗修正，可获得更为精确的加载压力历史。

基于已知材料动力学参数的铝电极板与LiF 窗口界面处的速度历史，通过式（2）波阻抗修正，应用简单波原理，计算精确的加载压力历史，计算流程见图3。

式中，Zs=ρ0scs(uw)表示在界面速度uw下的样品的初始密度与声速的乘积，即样品在界面速度uw时的波阻抗。Zw=ρ0wcw(uw)表示窗口在界面速度uw时的波阻抗。下标s 和w 分别表示样品和窗口，下标p 表示粒子速度，up为原位粒子速度。

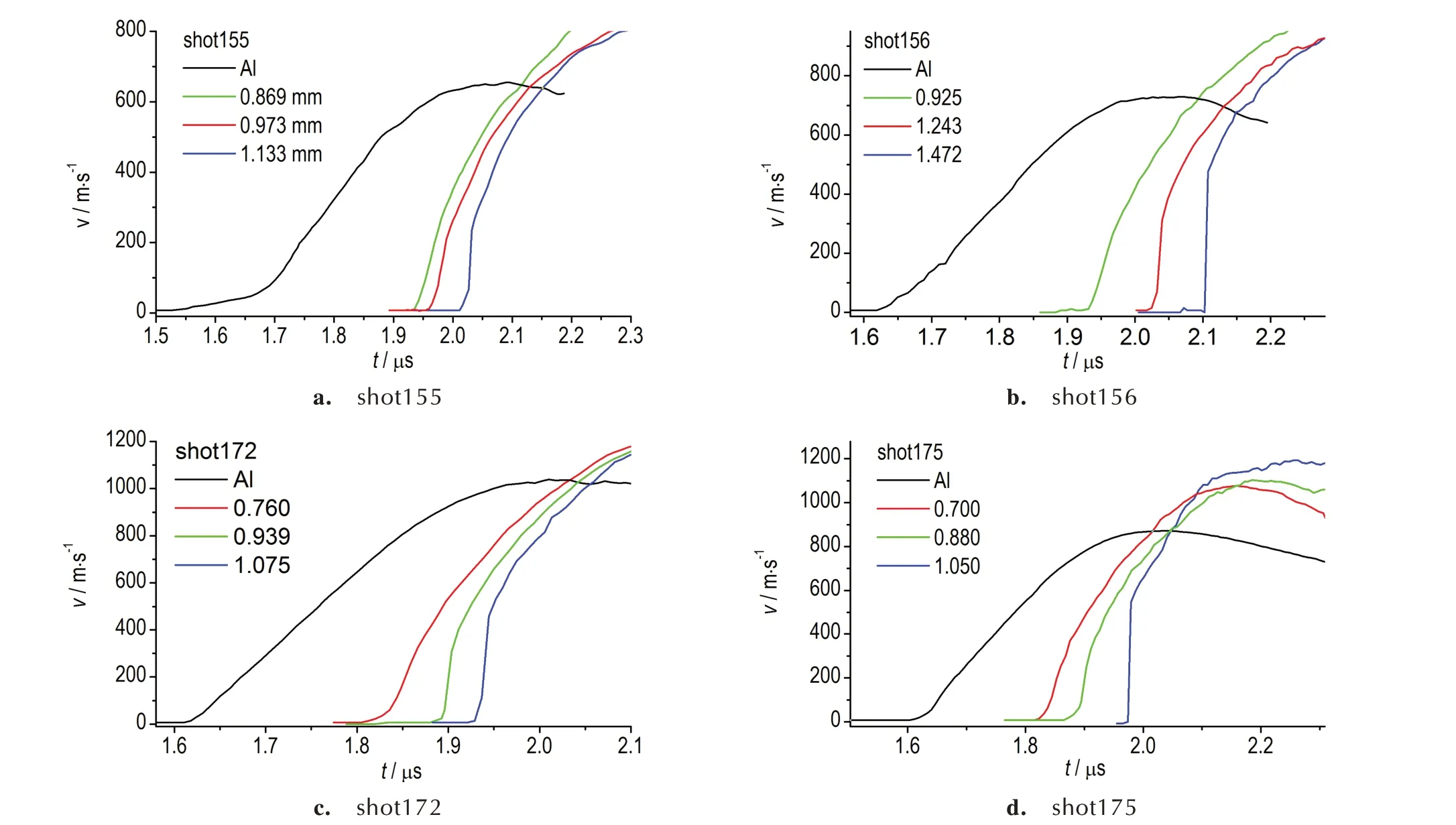
图2 4 发实验的速度历史曲线Fig.2 Interface velocities of four experimental shots

应用上述方法，由4 发实验中铝后表面速度曲线计算的压力时程曲线见图4 所示，4 发实验的压力峰值分别为10.8，12.2，18.5 GPa 和15.1 GPa。

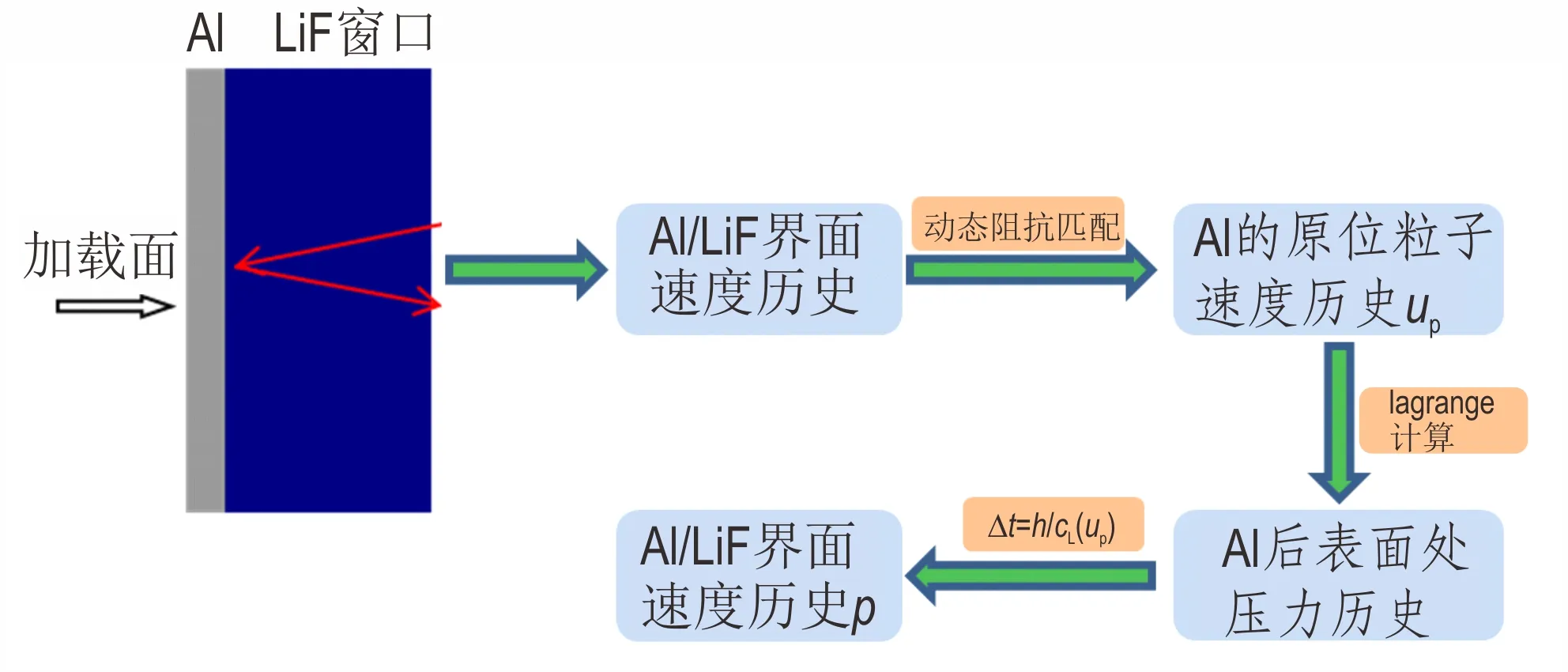
图3 波阻抗修正获取压力历史流程Fig.3 The flow chart of calculating pressure history with wave impedance correction method

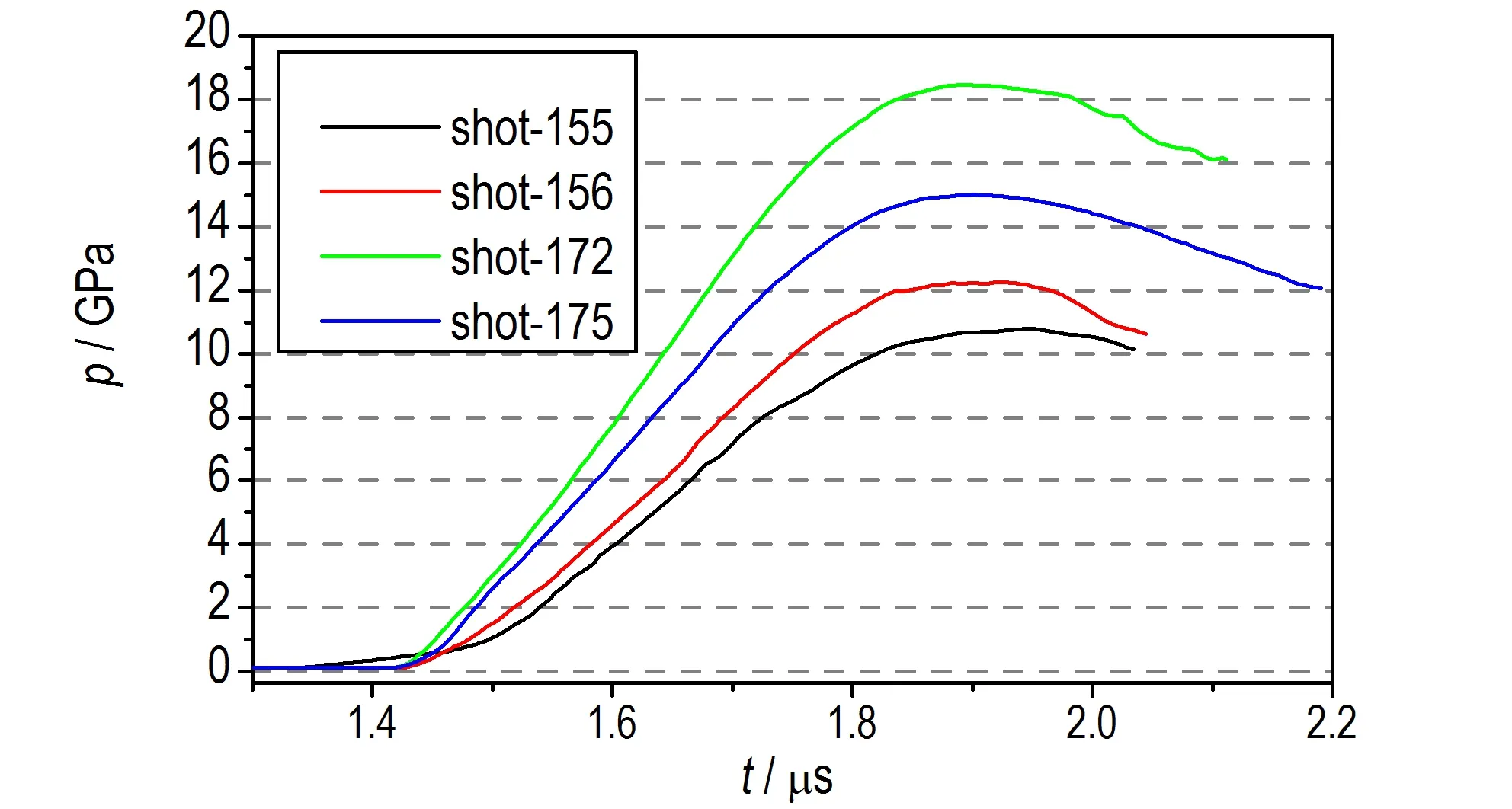
图4 4 发实验的加载压力历史曲线Fig.4 The loading pressure histories of 4 experimental shots

3 PBX-95 炸药的等熵状态方程、压力-比容关系和高压声速

材料的压力-比容关系、高压声速和状态方程是开展动力学数值模拟的基础，本节给出适用于斜波加载实验的数据处理方法，并计算PBX-95 炸药的动力学参数，给出适合斜波压缩过程的等熵状态方程。

同一发实验中，由于加载压力历史相同，两不同厚度样品的后表面位置可看作是同一无限厚样品中的不同空间位置x1、x2，在获知样品的原位粒子速度与时间的关系u-t的情况下，由平面一维等熵运动的质量、动量和能量守恒方程组，可得到如下的增量表达式［16］：

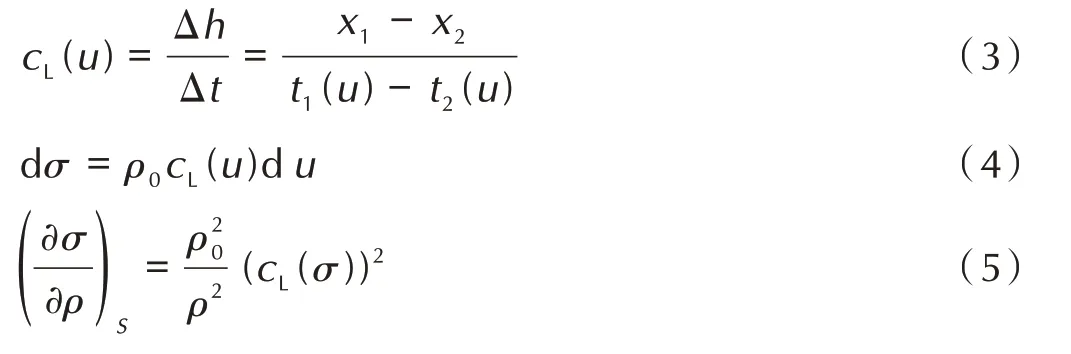
式中，cL为Lagrange 声速，Δh为样品厚度差，Δt为不同厚度处粒子速度达到相同速度的时间差，x1、x2分别表示样品1 和样品2 的厚度；t1(u)、t2(u)分别表示样品1和样品2 与窗口界面处样品的原位粒子速度达到u时所需时间，σ和ρ分别为样品中的应力和密度。

由于实验获得的速度历程是连续的，由式（3）可得到一定速度范围内的cL(u)的连续值。依据（4）式和（5）式，即得到等熵线上的斜率关系，积分可得材料的等熵线。忽略炸药材料强度，认为应力σ与静水压p相等，等熵线具体形式为：

式中，c0、s为是Hugoniot 关系参数；v、v0分别为材料比容和初始比容；ρ0为材料初始密度，g·cm-3。

公式（3）～（5）中的粒子速度均为样品的原位粒子速度，因此，需对带测试窗口的速度曲线进行处理，利用增量阻抗匹配（式2），修正样品与窗口阻抗失配的影响，获得原位粒子速度。

应用式（2）～式（5），对压力峰值最高的shot-172实验结果进行数据处理，经过多次迭代收敛，获得的PBX-59 炸药的Lagrange 声速与粒子速度关系曲线见图5，由图5 可见，PBX-59 声速与粒子速度关系近似表现为线性，对声速与粒子速度曲线进行线性拟合，得到的线性关系为CL=2.78+4.18up。对比式（1）所示的Lagrange 声速与粒子速度的关系，得到样品材料在0～18.5 GPa 的Hugoniot 关 系 参 数 为c0=2.78 km·s-1、s=2.09。

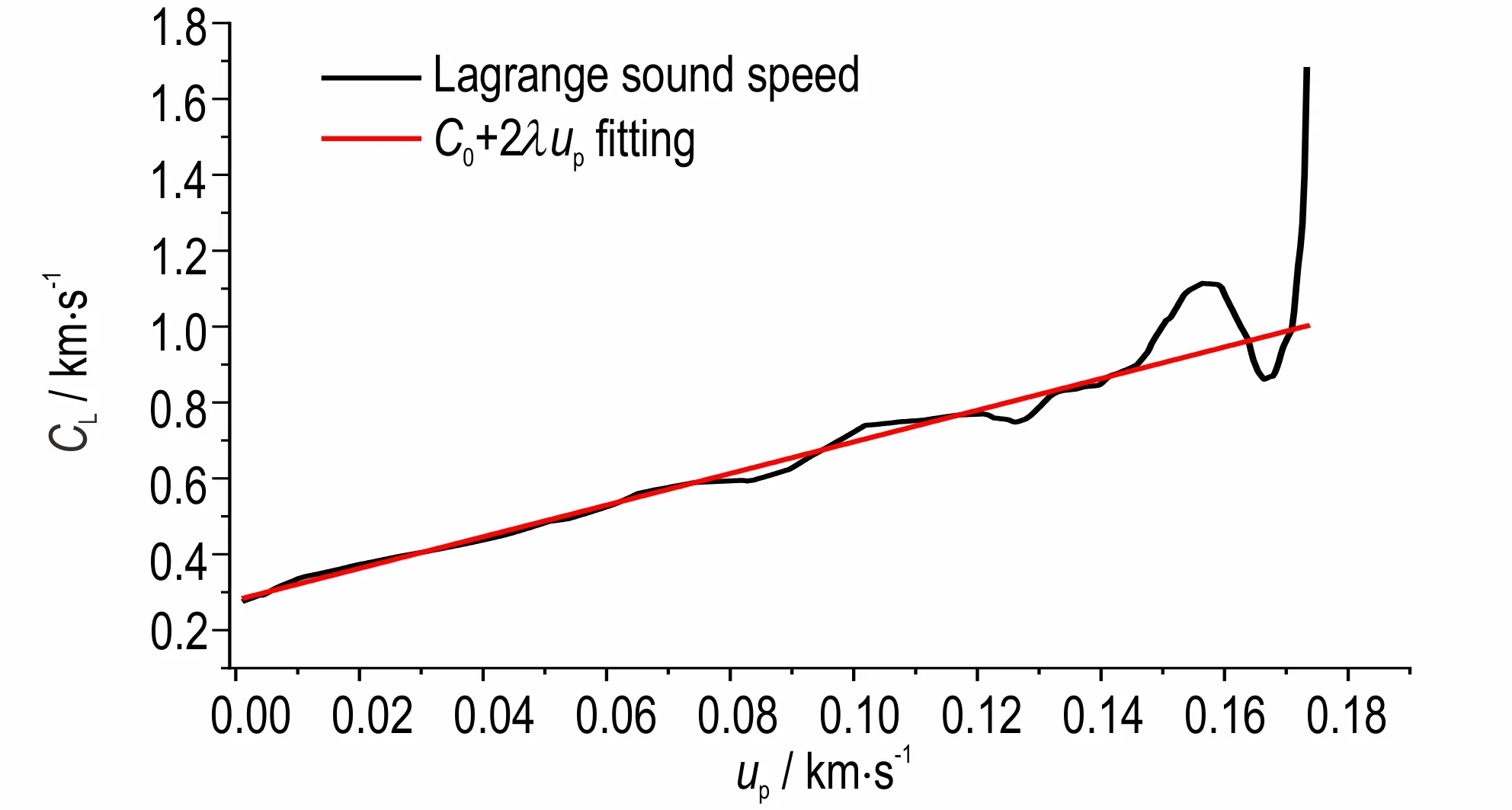
图5 PBX-59 的声速-粒子速度曲线Fig.5 The Lagrange acoustic velocity-particle velocity curve of PBX-59

联合式（1）和（4）可得到样品的斜波压缩压力-相对比容关系曲线，如图6 所示。为了比较，同时将董海山［13］、LASL 实验室［17］的结果绘于图中。由图6 可见，炸药表面粒子速度的抖动造成Lagrange 声速起伏，但由于积分效应，这种声速上偏离真实值的抖动会得到抑制，实验获得的压力-相对比容曲线与用Hugoniot关系式（6）计算结果基本重合，即使是声速尾段相对剧烈的抖动，在压力-相对比容曲线上仅表现为小幅变化。图6 结果与董海山院士早期利用楔形块和转镜相机结合测得该炸药在1.3～8.2 GPa 压力区间的冲击Hugoniot［13］线 在p-v/v0曲 线 上 基 本 重 合（绿 色 星 形点），该结果外推到高压段时（绿色虚线）与本实验结果存 在 明 显 差 异，与PBX-9501 炸 药［17］（95% HMX，2.5% Estane，2.5% BDNPFA，理论密度1.860 g·cm-3）的压力-相对比容线差异大很多，PBX-59 与PBX-9501两种炸药中的HMX 均占95%，但由于黏结剂种类不同，所以导致炸药理论密度和密实度的差异，动力学参数上的差异明显，故不能随意借鉴和使用。

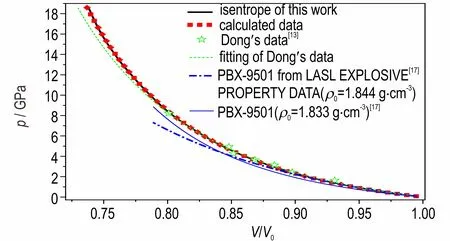
图6 PBX-59 和PBX-9051 的压力-相对比容曲线Fig.6 The pressure-relative specific volume curves of PBX-59 and PBX-9051

4 数值模拟

为了校核以上物理模型和实验获取的PBX-95 动力学参数，结合守恒方程和（6）式状态方程对本文4 发实验进行了流体动力学数值模拟，结果如图7 所示。铝电极和LiF 采用Grüneisen 状态方程［18］，具体计算参数见表2。

实验中未见明显的弹塑性转变，故计算未考虑材料的强度效应，参数列表于表2，其中，PBX-59 参数由上述实验获得，认为Gruneisen 系数Γ(v)/v= Γ0/v0，Γ0取值［2，21］1.15。对应实验的加载压力历史见图4，此处以真实时序开展模拟计算。

模拟计算与实验结果如图7 所示。由图7 可得，磁驱动准等熵压缩实验获得的PBX-59 炸药的状态方程参数能较好地再现18.5 GPa 内未反应炸药的动力学响应过程。在时序和波形两方面，计算的速度曲线均能与实验结果较好吻合。shot-175 实验中1.050 mm 厚样品中出现了明显的前驱冲击波，幅值达到550 m·s-1以上，速度曲线表现出比其他厚度样品更快的速度增长，不考虑化学反应的模拟计算无法再现实验结果，该样品中可能发生了明显的化学反应。

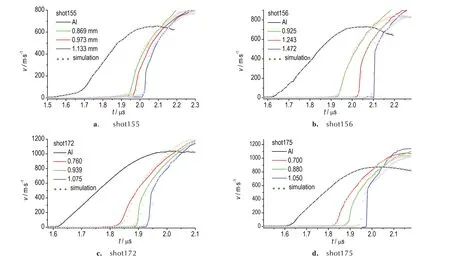
图7 模拟计算与实验结果对比Fig.7 Comparisons between calculated and experimental data

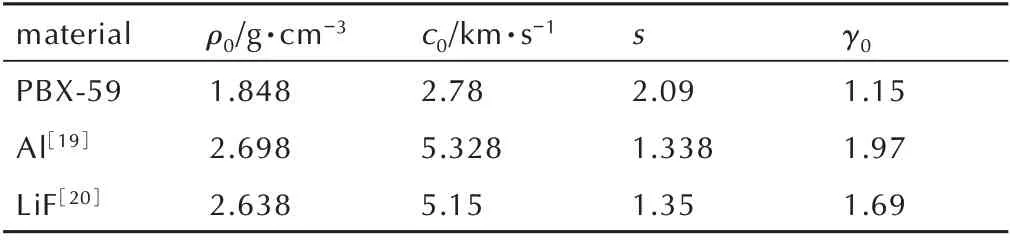
表2 一维流体动力学模拟计算参数Table 2 Calculation parameters for one-dimensional hydrodynamic simulation

5 结论

利用磁驱动斜波压缩加载实验技术，针对PBX-59炸药，分别从未反应固体炸药在磁驱动准等熵加载下的动力学实验、数据分析处理和数值模拟三个方面开展了动力学及状态方程研究工作。基于CQ-4 装置获得了0～18.5 GPa 峰值压力下PBX-59 炸药的动力学响应，利用迭代的Lagrange 数据处理方法获得了该炸药斜波压缩下的压力-比容关系及其参数和Lagrange 声速-粒子速度关系，给出了适合斜波压缩过程的等熵状态方程。结合等熵状态方程和实验获得的动力学参数，完成了实验过程的数值模拟，计算较好地再现了实验结果，验证了本文实验技术及其数据处理方法、物理模型及其参数的正确性。