基于禁忌搜索的作战重心分析与选择方法

2021-02-03张国辉杜正军周江平

火力与指挥控制 2021年1期

张国辉，杨征，杜正军，周江平

（1.解放军31004 部队，北京 100094；2.解放军31001 部队，北京 100091）

0 引言

“重心”在物理学上是指物体重量的集中作用点，不论物体的位置如何改变，物体的各部分都围绕着这一点保持平衡。重心概念由克劳塞维茨最早运用于军事领域［1-2］。克劳塞维茨认为“重心是一切力量与运动的中心，是一切事物的依靠。在战争中，应集中所有的力量打击这一点”［1，3］。

20 世纪90 年代美军将“基于效果作战（Effect Based Operation，EBO）”理论应用于战争实践以来，其他国家也纷纷开展了支持EBO 的作战计划制定方法的研究［4］。最典型的作战计划拟制过程为：作战重心确定→作战重心发现→作战行动方案制定→作战行动方案分析与评估→作战行动方案生成［5］，其中，重心发现是实现作战计划制定的关键［4，6］。由此可见，重心发现对于作战过程具有极其重要的作用。

目前，关于作战重心的定义还没有统一的概念。以美军为例，美军并没有一个统一的作战重心的概念，各军种有关重心的定义各不相同，而且有些定义内涵相差较大。如，美空军认为重心是敌人的主要弱点，是敌方作战体系内的一些最薄弱环节，对这些薄弱环节的打击将最有可能取得决定性的结果［4，7］。美陆军认为，重心是一切力量与运动的中心，是一切事物的依靠，是敌方或己方可以从中获得行动自由、物质力量和作战意愿的一种特点、能力或地方。美海军则认为重心是敌方的力量源泉，是敌方的强点，在作战过程中，应该间接而不是直接地攻击敌重心。在对重心概念众说纷纭的情况下，美军联合作战条令认为，重心是敌人总体能力的某些方面，它们一旦被攻击、压制或摧毁，从理论上讲将会导致敌人不可避免地陷入失败的境地，或者迫使敌人放弃其企图或改变其行为［3］。

近些年来，对作战重心的研究成果很多，文献［8］对美军基于重心理论的作战筹划方法进行了研究，分析了其理论来源、基本要素和推理过程。文献［9］指出，在高科技条件下作战重心已经发生了深刻的变化，呈现出重心目标配置分散化、重心目标群体系统化和重心目标性质多样化等特点。文献［4］研究了基于贝叶斯网络的火力打击重心分析建模问题，提出了相应的建模方法和流程。鉴于贝叶斯网络在解决复杂系统决策问题方面的优势，李正浩等［10］研究了一种基于贝叶斯网络推理的作战重心评估模型，并定量评估了各个作战环节的重要程度。文献［11］提出了基于作战重心理论的体系构建和评估方法，并研究了基于重心分析的联合作战计划制定过程。文献［12］研究了网点空间作战中的打击重心分析过程，给出了打击重心分析的基本原则。

综合对相关文献的分析，本文认为：作战重心，是军事网络中保障作战单元发挥其作战能力的关键力量，是作战活动中各种力量的合力点，是达成预定作战目的关键所在，是整个作战行动应解决的中心问题，也是军事网络中重要的组成部分，它是一个相对的概念，随着作战目的、打击手段、战场资源等因素的不同，作战重心也将随之改变。同时，还可以得出以下认识：

1）重心是敌方作战系统的重点，确定敌方作战重心是实施作战指挥的关键。重心位于战略和联合战役筹划的顶层，是筹划的基础。通过打击其作战重心，可以有效动摇敌方的作战决心、延缓敌方的作战行动［4］。

2）在信息化作战条件下，作战目标关联密切、种类繁多，如何在复杂战场环境下快速找到关键目标，是指挥员关心的重要问题［13］。如有可能应尽可能对敌重心实施直接进攻，但在作战过程中，敌重心可能不明显或不易判断，敌方也会竭力保护自己的重心，这使得直接攻击重心变得非常困难和难以实现。

3）作战重心是敌方保护的重中之重，很难直接进行火力打击［4］。因此，火力打击作战重心应当是从基于效果的角度对影响重心的要素进行分析决策，从而得到一系列能够使打击效果最大化的打击目标［4］。

4）作战重心的分析选择依赖于作战网络模型的构建，而作战网络模型根据作战场景和研究领域的不同，将呈现出不同的模型形式［14-16］。文献［17］在研究信息化条件下联合作战的作战模型时，将所有作战单元抽象为决策器（D）、传感器（S）和影响器（I）3 类节点。陈士涛等［18］则将作战网络抽象为指挥类（D）、侦察类（U）、打击类（A）和目标类（T）4 类节点。

1 问题描述

对于一般的作战网络结构，如果不考虑目标的打击代价，则作战网络的重心可以理解为是作战网络中网络影响力最大的节点或者边，若将这些节点和边删除后，作战网络的最大连通度变化量最大，即对作战网络的结构最具破坏性。但是实际上，战争不可能没有打击代价（如弹药消耗、人员伤亡、经费开支等），而且打击代价对于战争胜负往往具有决定性作用。因此，在进行作战重心分析时不能不考虑打击代价。当考虑作战网络的打击代价，并以总的打击代价（包括弹药消耗、经费开支）最小为重心选择的依据时，问题将变得十分复杂，必须构建能反映打击效果的作战模型，采用科学有效的方法予以分析求解。

为此，本文构建了考虑打击代价的目标重心分析与选择模型，且设计了相应的求解算法，并通过实验案例对模型和算法有效性及可行性进行了验证。

2 模型构建

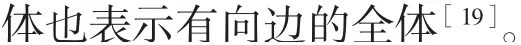
2.1 符号说明

2.1.1 集合

D：表示作战任务允许消耗弹药的上限，即作战过程中的弹药消耗不允许超过D 值；

E：表示参与作战的人员数量上限，即作战过程中的人员伤亡必须小于参战人数；

F：表示作战任务允许消耗的经费上限，即作战过程中的所有经费开支必须不超过F 值；

2.1.3 决策变量

xm：为0-1 变量，值为1 时，表示作战网络中第m 个节点（火力单元、情报单元或指控单元）被摧毁；否则值为0；

ykl：为0-1 变量，值为1 时，表示作战网络中第k 个节点和第l 个节点之间连边（火力单元与情报单元之间，指控单元与火力单元之间，或指控单元与情报单元之间的链路）被摧毁；否则值为0。

2.2 数学模型

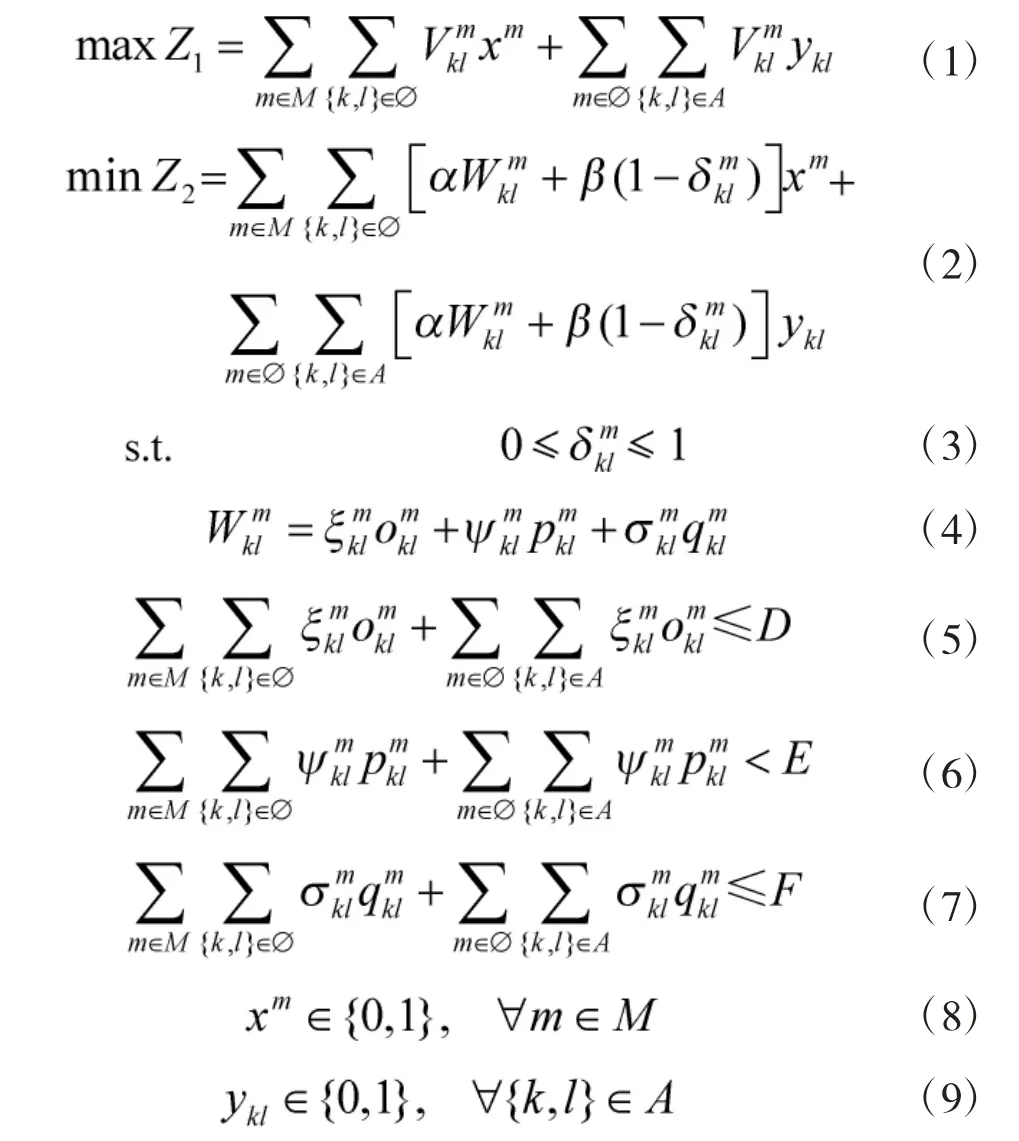
目标函数式（1）以作战网络节点的重要度和节点间连边的重要度之和最大化为优化目标，其中，函数式第1 项表示作战网络节点的重要度，第2 项表示节点间链路的重要度。目标函数式（2）以作战网络的节点和边的打击代价之和最小为优化目标，其中，函数式第1 项表示摧毁某作战单元的打击代价和毁伤概率，第2 项表示摧毁节点间通信链路时的打击代价和毁伤概率。

约束条件式（3）表示作战网络节点和节点之间连边的毁伤概率在［0，1］之间取值。约束条件式（4）表示弹药消耗数、人员伤亡数和经费开支等因素，共同构成了作战打击代价的考虑因素，几个因素的重要程度依据战争任务、专家评估及指挥决策的变化而定。式（5）～式（7）分别表示弹药消耗、人员伤亡和经费开支的数量约束。另外，约束条件式（8）和式（9）分别表示xj和ykl是0-1 变量。

3 禁忌搜索算法设计

作战网络重心选择优化模型是整数规划问题，问题规模较小时可以用CPLEX 进行求解，但当问题的规模增大时，若继续采用CPLEX 进行求解，计算时间将迅速增长。而且上述优化问题属于多目标优化问题，求解多目标优化问题通常可以采用NSGA-II 算法。本文借鉴标准NSGA-II 的基本思想，采用禁忌搜索算法（Tabu Search，TS），针对作战网络重心选择优化模型的特点进行了算法设计。

禁忌搜索算法是一种启发式算法，它是一种全局逐步寻优的算法，是对局部邻域搜索的扩展。禁忌搜索算法通过设计灵活的数据结构和对应的禁忌准则来有效避免重复搜索，并通过特赦准则来赦免某些被列入禁忌表的良好状态［20］，且当前解还可以通过一定方式接受劣解［21］，从而保证搜索的多样性，力求实现全局最优化［19］。禁忌搜索算法在解决全局优化问题和组合优化问题中展现了良好性能，已经被成功运用于求解车间调度问题、旅行商问题等［22-23］。本文结合作战网络的特点，采用禁忌搜索算法的良好特性［23］，设计一种解决作战网络重心分析问题的改进的禁忌搜索算法。

通常情况下，要设计禁忌搜索算法，需要确定以下环节：1）初始可行解及评价函数；2）邻域结构和禁忌对象；3）候选解选择［24］；4）禁忌表及其长度；5）特赦规则［24］；6）集中性和多样性搜索策略；7）终止准则［25］。

3.1 初始解的构造

较好的初始可行解可提高算法在解空间搜素的效率［2］。在构造初始解时，先通过指标ω 对所有链路进行排序，选择ω 值最大的n 条链路作为初始作战重心，然后根据选定的n 个初始作战重心作为初始解。

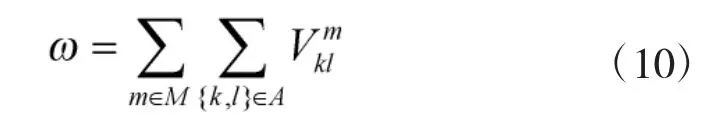
在构建指标ω 时，主要出于以下考虑，虽然作战重心的选取与重要度、打击代价和毁伤概率都有关系，但在这几个因素中，仅有重要度因素与作战网络的网络结构密切相关，而对作战网络结构的分析还原是一个动态的过程，作战网络结构的实时变化必将引起重要度的改变。因此，用重要度作为初始解构造指标可以较好地体现链路重要度变化特点。

3.2 评价函数

改进的禁忌搜索算法的评价函数用于对搜索状态的评价，结合禁忌规则和特赦规则来选取新的当前解。为更好地描述评价函数的基本设计思想，引入下列数学符号：

Hk：表示第1 个优化目标函数的第k 次迭代所得解；

rfirst：表示当前解Hk中重要度最高的那个候选作战重心；

rsecond：表示当前解Hk中重要度次高的那个候选作战重心；

ΔZk+1：某个候选作战重心的状态发生变化时，第1 个目标函数值的变化量。

改进的禁忌搜索算法评价函数可使用如下规则［25］：

1）对于Add 过程，评价函数为

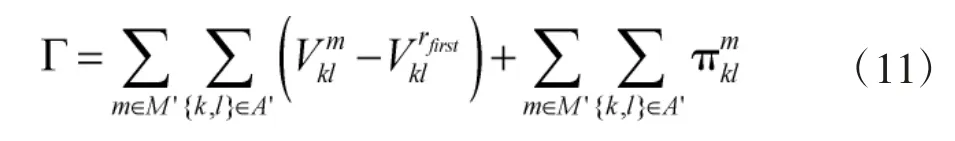
Add 过程具有如下性质：

性质1 如果在k+1 次迭代时加入一个候选作战重心i，则目标函数变化量为［25］

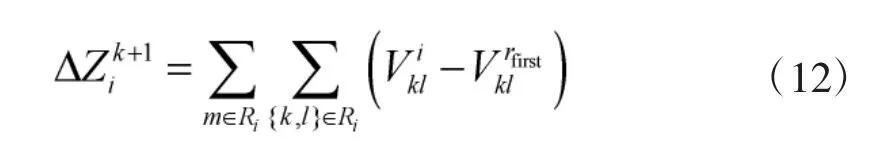
证明：当向解Hk中加入一个候选作战重心i时，目标函数变化量为

证毕。

2）对于Drop 过程，评价函数为过程，评价函数为

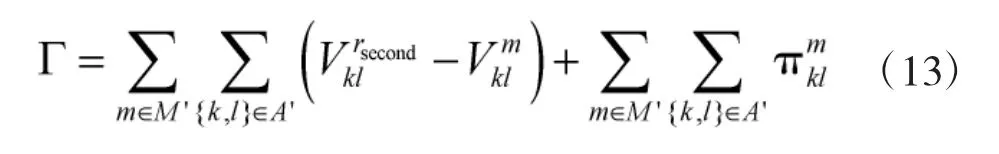
Drop 过程具有如下性质：

性质2 如果在k+1 次迭代时删除一个候选作战重心i 时，则目标函数变化量为［25］

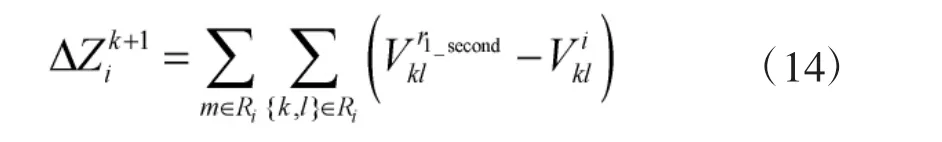
证明：当从解Hk中删除一个点i 时，目标函数变化量为

证毕。

3.3 邻域结构及其候选解

邻域结构是指从一个给定解跳转到另一个解的规则［22］。邻域解是由给定解经过一次跳转所得到的，局部搜索过程中如何从一个解跳转到另一个解是由其邻域结构决定的，因此，邻域结构的构造方式直接影响到局部搜索算法的效率［22］。结合作战网络重心分析问题的特点，本文的邻域移动是针对候选作战重心进行的。

3.4 禁忌长度及禁忌对象

3.5 特赦规则

本文采用的特赦规则是：1）假如某个禁忌的候选解优于当前最好解，则将此候选解解禁，并将其选为当前最好解［27］。2）假如禁忌候选解和非禁忌候选解都不优于当前最好解，则将最好的非禁忌解选为当前解。3）假如所有候选解都被禁忌，而且不存在优于当前最好解的候选解，则对最好的候选解进行解禁操作，并将其作为当前解，以便继续搜索［21］。

3.6 停止规则

一般而言，禁忌搜索算法的常用停止规则有：1）迭代次数达到预设的最大迭代次数［19］。2）目标函数值持续未得到改善。3）运算时间达到预设的运行时间［28］。4）目标函数值达到预设值等［19，21］。本文将停止规则设定为运算达到预设的最大迭代次数［19，27］。

3.7 算法流程

至此，本文采用禁忌搜索算法的基本思想进行作战网路作战重心的重要度搜索，能有效地对具有大规模作战单元的作战网络进行分析。但是，本文所构建的考虑打击代价的作战重心分析模型包含两个优化目标：一是作战单元或链路的重要度最大；二是打击各作战单元和链路的打击代价最小。刚通过禁忌搜索算法进行的求解，仅解决了依靠重要度得到作战网络重心的优化目标，接下来还需要考虑打击代价对于作战网络重心的影响。为此，本文借鉴标准的（Non-dominated Sorting Genetic Algorithm II，NSGA-II）算法思想，并结合考虑打击代价的作战重心分析问题的特点，进行了调整及改进，具体计算流程如下，算法流程图如图1 所示。

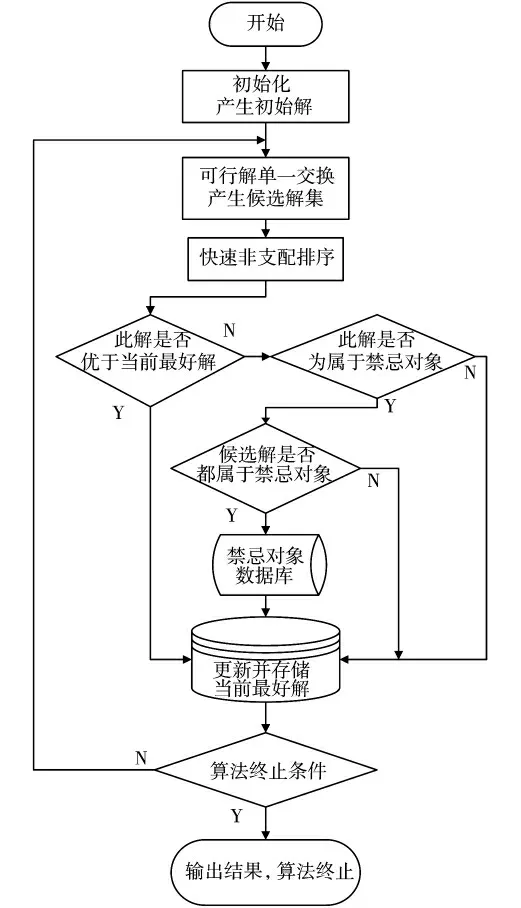
图1 算法流程图

Step 1 应用上述初始解的构造方法产生初始解，并设为当前解和当前最优解。

Step 2 依次将非候选作战网络重心与候选作战网络重心集合中的可行解作单一交换，产生候选解集。

Step 3 从候选解集中选择最好的解，快速非支配排序，若此解优于当前最好解，转至Step 6；否则转至Step 4。

Step 4 判断解是否为属于禁忌名单，若属于则转至Step 5；否则转至Step 6。

Step 5 假如所有的候选解都属于禁忌名单，则把最好的候选解选作当前解，转至Step 6；否则将非禁忌的最好候选解选作当前解，转至Step 7［29］。

Step 6 对当前的解进行更新，并保留当前最好解。

Step 7 对禁忌名单进行更新。

Step 8 判断是否达到算法停止条件，若是则输出结果，计算结束；否则转至Step 2。

4 实验验证

4.1 实验设置

为检验模型及算法的有效性及合理性，设定如下背景：某场战争中，通过侦察等技术手段，还原和重构了敌方的作战网络，该作战网络包含有60 个作战单元，大致区分为3 种类型：指控节点C2，火力节点F，情报节点I，各节点间的连接关系如图2所示。

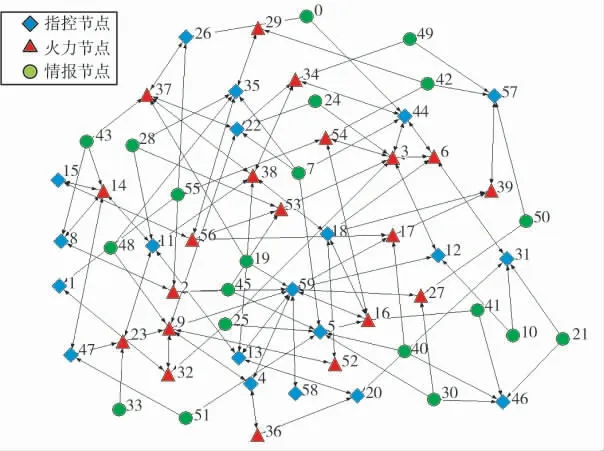
图2 60 个作战单元的作战网络示意图

每个作战单元的重要度、打击代价和毁伤概率采用随机生成的方式产生，列于表1 中。作战网络图中各节点之间的连边表示各作战单元之间由信息交互关系。不失一般性，设“打击代价”占节点（连边）重心分析中的权重值α=0.5，设“毁伤概率”占节点（连边）重心分析中的权重值β=0.5。

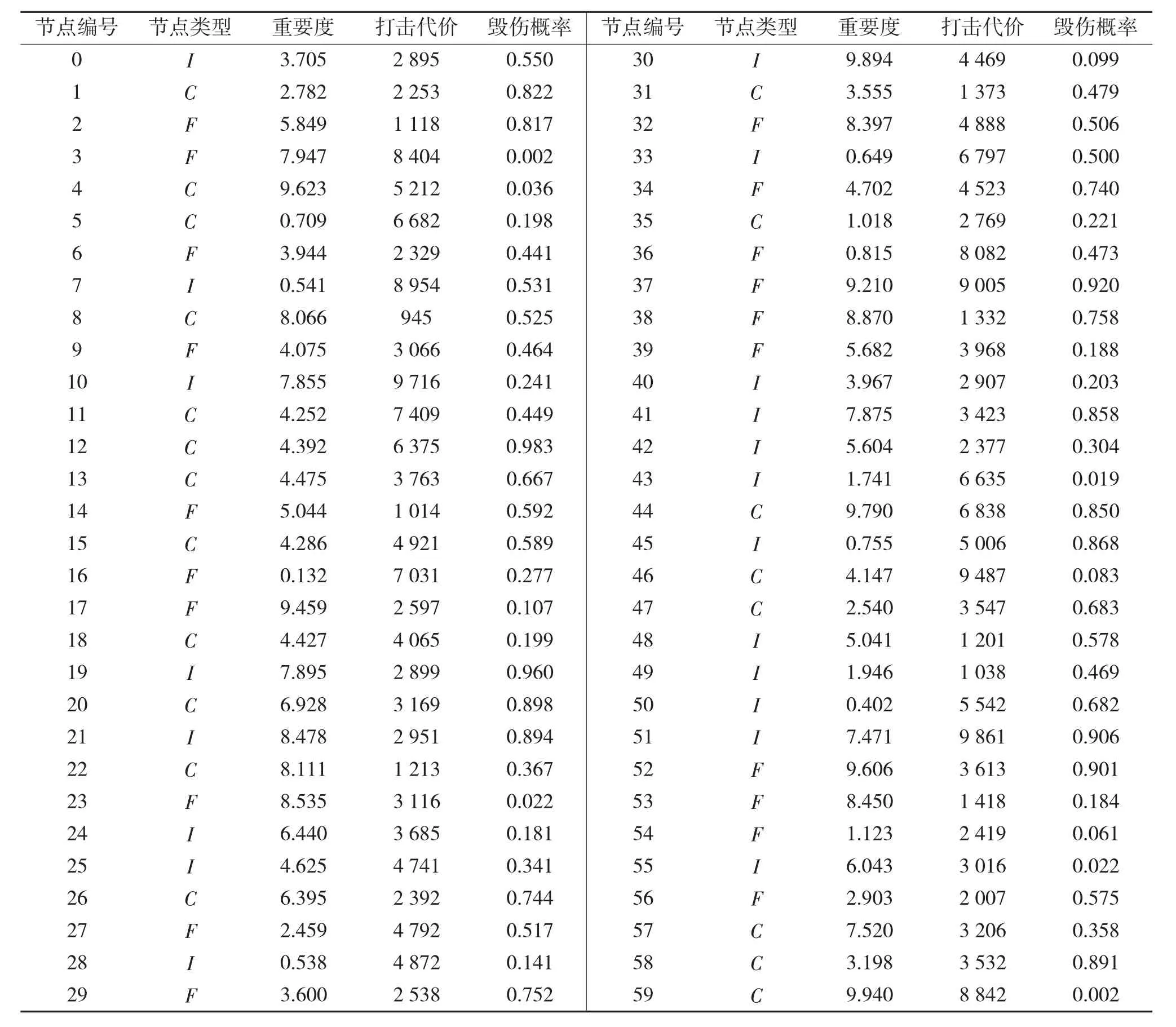
表1 60 个作战单元的特征属性值

利用前面给出的模型及求解方法，可以计算出该优化问题的最优解，即最优重心节点为第44 号节点，最优的作战重心链路为：1→32→9→4→36→20→13→11→14→15→56→17→39→18→6→44→0，且该最优解的目标值1 为0.889，目标值2 为2 097，结果如表2 所示。

表2 最优作战重心选择方案及目标值

4.2 实验分析

为了进一步分析“打击代价”因素对于作战网络重心选择的影响，按如下实验步骤进行分析：

Step 1 在求解过程中，先计算考虑打击代价时的可行解，并按可行解重要度降序排序，选取前30组可行解，将其定义为变量Opt01；

Step 2 在求解过程中，不考虑打击代价，仅依据节点（连边）重要度进行重心分析，按照重要度大小将可行解进行降序排序，选取前30 组可行解，将其定义为变量Opt02；

Step 3 运用IBM SPSS Statistics 19.0 对上述步骤所得样本及变量进行统计分析。对变量Opt01 与变量Opt02 进行假设检验，用于检验打击代价因素加入前后，两组可行解之间的差异是否具有统计学意义［30］。本文选择的假设检验的方法是成对样本t 检验，且检验水平为0.05，检验结果如表3、表4 及图3 所示。

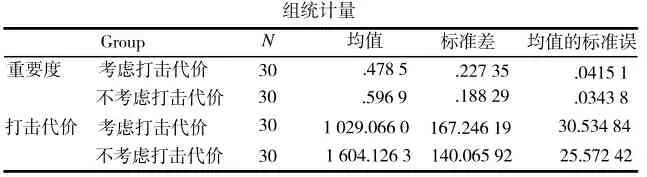
表3 两组可行解描述统计结果

如表3 所示，对于第1 个优化目标，当不考虑打击代价时，30 个样本的重要度平均值为0.60，而考虑打击代价时，样本的重要度平均值为0.48。显然，不考虑打击代价因素时，选出的作战重心的重要度相对较高。对于第2 个优化目标，当不考虑打击代价因素时，30 个样本的实际打击代价平均值为1 604，而考虑打击代价因素时，样本的实际打击代价平均值为1 029。显然，考虑打击代价因素时，选出的作战重心的实际打击代价将大大降低。素时得出的实际打击代价值远低于不考虑打击代价时的分析结果，可见，考虑打击代价因素对于降低作战单元实际打击代价具有显著意义。

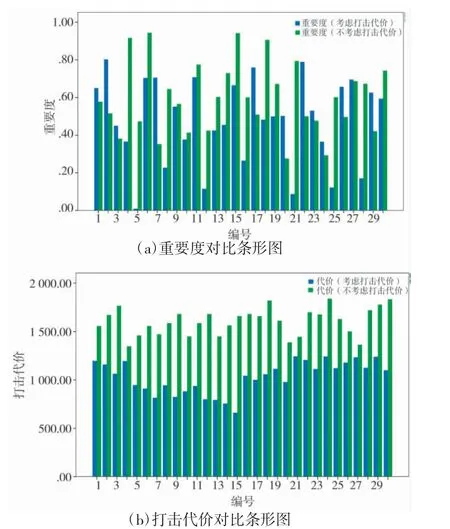
图3 考虑打击代价因素前后两组可行解的描述统计分析

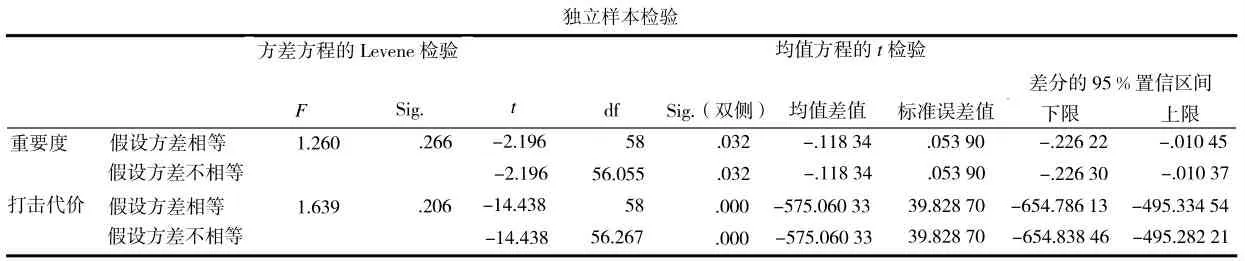
表4 两组可行解的独立样本t 检验结果

表4 则进一步反映了打击代价因素加入前后，两组可行解样本之间的差异程度。如表可知，两组样本的重要度成对t 检验统计量为-2.196，打击代价的成对t 检验统计量为-14.438，所对应的差异显著性检验值分别为P=0.032，P=0.000 且均满足P＜α=0.05，因此，认为两组样本的重要度之间以及打击代价之间具有统计学意义。其中，打击代价的成对t检验显著性检验值为0.000，远小于0.05，从而进一步印证了考虑打击代价因素对于降低作战单元实际打击代价具有显著意义。