航空结构件孔边裂纹监测技术研究综述

于翀 宋昊

摘要：孔边裂纹问题一直是影响铆接、螺栓连接等结构安全性能与剩余寿命的一大因素，同时对孔边裂纹的监测也是飞机结构健康监测的重要环节。从最初对孔边裂纹的无损检测技术到目前的孔边裂纹实时监测技术，对含孔结构的研究一直是众多科研人员的研究重点。本文结合相关文献对现有孔边裂纹监测技术进行了总结，从数据计算分析法与传感器实时监测法两方面对现有的孔边裂纹监测技术进行了介绍。最后，根据国内外孔边裂纹监测技术的研究现状，从研究方法归纳整理、新型传感器设计、传感器封装、技术融合、健康管理5个方面进行了展望，为今后航空关键结构件的孔邊裂纹监测技术研究与发展提供了参考。

关键词：孔边裂纹；结构健康监测；数据计算分析；传感器实时监测；健康管理

中图分类号：V219文献标识码：ADOI：10.19452/j.issn1007-5453.2021.12.001

基金项目：航空科学基金（20185644003）

由于现代工业科技的快速发展，工程结构的连接方式变得多种多样。但是铆接、螺栓连接由于其使用简单、便于拆卸等优点依然被使用，同时也是航空领域中常用的紧固件，在飞机装配过程中得到广泛应用[1-2]。

据统计，在飞机装配过程中由铆接、螺栓连接的结构占飞机机身结构的70%以上，螺栓连接或者铆接结构在起落架、机身蒙皮、飞机发动机等部位随处可见。然而飞机在飞行过程中所处的环境复杂，受力情况千变万化，在铆接、螺栓连接的部分区域会产生严重的应力集中现象，导致铆钉孔或螺栓孔产生孔边裂纹。同时，飞机在飞行或地面停放过程中，由于湿度大、温差大甚至酸雨的影响，使飞机的内部结构产生腐蚀，这些腐蚀现象也会导致孔边裂纹现象的发生[3-8]。

由机体疲劳失效造成的飞机事故中，有近80%的疲劳裂纹产生于结构件铆钉孔区域，所以及时发现孔边裂纹的萌生并预测其发展趋势，对于改善飞机结构性能、减少飞机关键部位断裂故障，以及防止重大空难事故的发生具有重大意义。目前，用于检测孔边裂纹的技术有多种，如超声检测技术、红外检测技术、涡流检测技术、射线检测技术、数字图像检测技术等[9-17]。但是这些无损检测技术主要适用于零部件装配前或裂纹产生后进行检测，无法实现对孔边裂纹实时监测。现有用于孔边裂纹实时监测的技术大致可以分为两类：一类是采用数学函数、有限元或其他分析方法对某一条件下的孔边裂纹模型进行计算分析，得到裂纹扩展的相关数据，根据数据的变化情况判断孔边裂纹扩展形式以及剩余寿命；另一类是采用传感器对铆钉孔或螺栓孔进行实时监测，并将采集到的数据进行处理，以此来判断孔边裂纹的扩展情况以及剩余寿命。

1数据计算分析法

数据计算分析法主要指通过数学计算、有限元或边界元方法对某些情况下的孔边裂纹进行分析，并通过计算得到能够表征孔边裂纹扩展情况以及剩余寿命的相关参数，通过对参数的分析进行对孔边裂纹萌生、扩展的预测。数据计算分析法具体可分为应力强度因子分析法与粒子滤波分析法。

1.1应力强度因子分析法

应力强度因子反映了裂纹尖端附近应力强弱程度，主要受到孔自身应力集中与裂纹长度的影响。所以根据应力强度因子的变化情况可以判断出孔边裂纹的萌生与扩展情况。对于铆钉孔、螺栓孔简单的孔边裂纹扩展过程，可以通过数学分析的方式求出应力强度因子；而对于比较复杂的孔边裂纹扩展过程，若仍然采用数学分析方法则需要进行大量的数学计算，此时这种方法便不再适用，就需要通过有限元建模仿真或边界元方法来计算应力强度因子的具体数值。

1.1.1数学分析求应力强度因子

利用数学分析的方式求应力强度因子目前主要是通过复变函数、权函数或积分法对孔边裂纹模型进行数学变换以构造计算应力强度因子的公式，并利用所得公式对某些情况下的孔边裂纹进行裂纹扩展分析。

（1）复变函数法求应力强度因子

利用复变函数求解应力强度因子，首先要根据不同的裂纹形式以及边界条件构造复变应力函数，然后根据此复变应力函数对裂纹尖端的应力应变场进行分析，得到应力强度因子的表达式，以此求得应力强度因子的具体数值。保角映射函数是复变函数理论之一，具有将复杂区域转化为简单区域的优势，是利用复变函数计算孔边裂纹应力强度因子的有效工具。

Bowie[18]首先利用保角映射函数理论开始了对孔边裂纹问题的研究，通过对孔边裂纹模型的转化得到了应力强度因子；张永元等[19-20]在多孔边裂纹问题研究中应用了复变应力函数的叠加解法求解应力强度因子，并利用数值算例验证了此方法的适用性；赖俊彪等[21]采用复变函数方法得到了含孔边双侧直线裂纹有限大板应力与位移的全场表达式，并应用变分原理求解了应力强度因子与应力集中系数，而傅东山等[22]对上述方法加以改进，只计算了应力强度因子，省去了应力集中系数的计算，达到了同样的效果，提高了在求解孔边裂纹应力强度因子的计算效率；赵晋芳等[23]采用复变应力函数、近似迭代法与局部修正因子法求解了无限板共线多裂纹的应力强度因子；郭怀民等[24]构造保角映射对不对称椭圆孔孔边裂纹问题进行分析，得到了裂纹尖端的应力强度因子解；Iida等[25]用复应力函数中的相关理论对承受无限远处均匀横向载荷的含菱形孔无限大薄板进行了研究，求解了菱形孔在一定转角和裂纹长度范围内的应力强度因子。

在采用复变函数法求解应力强度因子时，对于简单的孔边裂纹扩展模型只需要确定一个解析函数，对于略微复杂的几何形状，通过保角映射也可以求解，大大减少了工作量。但是复变函数法一般用来求解含孔的“无限大”弹性平面的孔边裂纹问题，然而当求解弹塑性或者三维问题时，构造复变函数变得极其困难，此时复变函数法便不再适用。

（2）权函数法求应力强度因子

权函数在计算应力强度因子时将几何因素与载荷因素进行了变量分离，通过孔边载荷的分布就可以对孔边裂纹进行分析，是一种高效、求解精度可靠的方法，在求解复杂应力场中裂纹强度因子问题被广泛使用。

吴学仁等[26-28]利用边缘裂纹权函数封闭解法，得到了各种基本载荷作用下孔边裂纹的应力强度因子计算公式，并计算出了复杂应力场中圆孔边穿透裂纹问题的应力强度因子权函数解析解；宋大毅等[29]在研究受均匀内压作用的偏置孔孔边裂纹问题时，将权函数与光弹性法相结合，对应力强度因子进行了计算；谢伟等[30]为了研究椭圆孔曲率半径对应力强度因子的影响，应用组合法的思想构造了椭圆孔边裂纹的权函数并给出了孔边三维角裂纹应力强度因子的求解方法；李政鸿等[31-33]从单一孔边裂纹和无限板中心裂纹权函数出发，提出了分析单孔孔边两条不等长裂纹的近似权函数法，并对孔边两条不等长裂纹在不同载荷下的应力强度因子进行了分析。同时，对于等效夹杂理论和相变增韧原理，李政鸿等还提出了对单孔两条不等长裂纹的应力强度因子修正，以获得多孔中单一孔出现两条裂纹的应力强度因子的分析方法，为孔边裂纹的应力强度因子分析提供了新方法；童第华等[34]提出了一种具有精确闭合解的权函数方法来计算无限大板和有限宽板中孔边萌生裂纹的裂纹面位移，验证了权函数方法在孔边裂纹扩展预测中的实用性。

权函数法求解应力强度因子虽然普适性大，求解效率高，在某些问题的求解甚至优于有限元、边界元等建模分析法，但是由于其依然为数学方法，在求解复杂问题时，巨大的计算量依然是其应用的一大阻碍。所以权函数法在求解二维问题时确实是有效的方法，但是面对三维问题时权函数法则需要考虑更多因素，变得更加复杂，限制了权函数法在求解三维问题的应用。

（3）积分法求应力强度因子

利用积分对应力强度因子求解的方法多种多样，可利用复变函数法或权函数法得到的部分解析式进行积分得到对应力强度因子的解，也可以通过各种积分变换公式对方程进行处理得到应力强度因子的解。

Tweed等[35]采用梅林变换对不同载荷下的孔边裂纹进行研究，计算了不同情况下的裂纹尖端的应力强度因子；郭万林等[36]根据功共轭积分原理对含中心孔的平板在多种载荷同时作用时的孔边裂纹进行了研究，并采用自选步长辛普森数值积分法计算出了應力强度因子；同时，郭万林等[37]还对孔边穿透裂纹应力强度因子、孔边角裂纹应力强度因子进行了计算，并分析了影响计算准确度的相关因素；李新平等[38]将无限弹性体内孔边线状裂纹的相关条件利用叠加原理和梅林变换进行了转化，并以弗雷德霍姆积分方程的解表示孔边裂纹扩展动态应力强度因子；郭俊宏等[39]在研究无限大板中椭圆孔边单裂纹受冲击载荷作用下的动态问题时利用柯西积分公式求解了在拉伸与剪切载荷下的应力强度因子的解。

利用积分法求应力强度因子虽然在一定程度上弥补了复变函数法或权函数法的某些不足，而且各种方法综合使用对计算精确度有一定提高，但是积分法是基于复变函数法或权函数法的部分计算结果进行积分变换，对于比较复杂的问题若无法应用复变函数法或权函数法，则积分法的使用便受到了限制。

1.1.2有限元建模计算应力强度因子

利用有限元建模计算应力强度因子主要是通过有限元建模软件建立孔边裂纹模型，并对裂纹萌生扩展过程进行仿真，结合其他分析方法得出应力强度因子的变化趋势。通过应力强度因子的变化趋势来判断孔边裂纹的扩展情况以及预测裂纹扩展趋势。目前，位移外推法和积分法是在完成有限元建模后计算应力强度因子的主要方法，同时还有部分学者利用其他方法实现了对应力强度因子的计算。

（1）位移外推法计算应力强度因子

位移外推法是求解应力强度因子的一种常用方法，此方法操作方便，计算简单。在完成对孔边裂纹模型的有限元建模后，由线弹性断裂力学理论可以得到裂纹尖端位移场的表达式，再通过外推法就可以得到裂纹应力强度因子。

Santhanam等[40]、Gong等[41]研究了含中心孔或偏心孔的有限窄板/带在远场均匀弯矩作用下的孔边裂纹问题，结合孔的几何形状、应力梯度以及位移外推法计算出了孔边裂纹的应力强度因子；沈海军等[42]对无裂纹及孔边含裂纹的锪窝孔结构进行有限单元模型分析，将二维裂纹位移表达式应用于三维裂纹中，得到了90°、120°锪窝孔边扇形角裂纹的应力强度因子，以及裂纹长度与应力强度因子之间的关系；王立清[43]采用有限元分析软件对4种孔边裂纹问题进行了研究，结合罚函数法与裂纹位移得到了不同情况下的应力强度因子；江勇[44]通过有限元软件的接触算法模拟了销钉和耳片之间的作用，通过1/4节点位移外推法得到了耳片裂纹尖端应力强度因子；王艾伦[45]以沉头铆钉过盈装配孔边角裂纹为研究对象，利用有限元分析软件建立了线弹性情况下开孔板与铆钉的干涉挤压模型，同样采用1/4节点位移外推法计算锪窝圆孔边扇形角裂纹的应力强度因子；龚德志等[46]建立了单个锪窝孔双边对称角裂纹有限元模型，通过裂纹裂尖位移表达式推出了裂纹前缘应力强度因子表达式，并实现了有限元模型的自动更新与裂纹扩展全过程的自动分析；王海等[47]对龚德志等提出的方法进行了改进，实现了锪窝孔多裂纹监测。

位移外推法不对裂纹尖端的应力强度因子进行直接求解，而是通过裂纹线上其他节点的位移推导出裂纹尖端的应力强度因子。此方法计算简单，对有限元模型的节点信息进行了充分的利用，节约资源。但是使用位移外推法求解裂纹尖端的应力强度因子时，有限元模型的网格尺寸对求解精度影响很大。同时，位移外推法的使用情况也有限制，此方法一般适用静态线弹性情况下的应力强度因子求解。

（2）积分法计算应力强度因子

结构承受过大的载荷会逐渐断裂，裂纹附近会存在应力场、应变场以及位移场，在这些力学场的基础上增加一个虚拟的辅助场并进行叠加得到复合场，利用复合场就可以求出能够反映场强的J积分。在有限元中的积分法求解应力强度因子多采用J积分法，以及由J积分法演变而来的相互作用积分法、M积分法等。

Stern等[48]首先提出了有限元分析中的交互积分法，对于二维复合型的应力强度因子可从能量角度求解；Dolbow等[49]将交互积分法进一步扩展，实现了对三维裂纹应力强度因子的求解；郁大照等[50]利用有限元分析软件中的J积分法对含多处损伤的某型飞机增压舱蒙皮搭接接头进行了应力强度因子求解；张文东等[51]对多孔等长裂纹、多孔主裂纹等5种开裂模式采用J积分法分别求解裂纹应力强度因子；云双等[52]对机身蒙皮天线通过孔的孔边裂纹建立了修理结构的有限元模型，同样采用J积分法求解了应力强度因子；孙晓娜等[53]通过有限元软件中的相互作用积分法求解应力强度因子，对有孔边倒角与无孔边倒角两种情况下的应力强度因子进行了有限元分析；李岩等[54]采用相互作用积分法结合有限元软件对孔边单侧裂纹承受拉力情况时的应力强度因子进行计算，并根据应力强度因子的最大值找到了裂纹最先扩展与破裂的位置；吴庆涛等[55]针对不同角度的初始孔边裂纹扩展问题，将有限元建模软件与断裂力学分析软件联合仿真，通过M积分法得到了三维模型中所有节点的应力强度因子；邹君等[56]对含有不同裂纹长度、铆钉类型、损伤模式的搭接结构进行了研究，通过有限元建模以及交互积分法得到了不同情况下的应力强度因子。

由于很多积分法是基于J积分法演变而来的，所以这些方法具有很多与J积分法相同的性质。J积分不仅适用线弹性断裂分析，也适用弹塑性断裂分析，应用广泛。由于J积分与积分路径无关，当对裂纹尖端过于复杂的应力应变场进行分析时，可以选择其他路径进行分析，大大降低了求解难度。而且通过有限元积分法得到的应力强度因子与解析解的误差最小，精度最高。但是在进行有限元积分法求解时需要加入虚拟辅助场，增加了计算量。同时，也正因为J积分与积分路径无关，所以如何选择合适的积分路径也是一个难点，这是有限元积分法的优点也是其缺陷所在。

（3）其他方法计算应力强度因子

除了上述内容介绍的有限元位移外推法、有限元积分法求解应力强度因子以外，还有很多学者提出了很多新的求解方法或者将几种方法综合使用，均达到了很好的求解效果。例如，孙益军[57]将有限元、弹塑性断裂力学以及疲劳断裂理论综合使用，对4种典型多部位损伤形式的应力强度因子进行了分析与计算；Zhao等[58]利用有限元分析软件对含中心裂纹、单孔边裂纹和两个对称孔边裂纹的无限大板试样进行了分析，分别采用位移相关法、J积分法、虚拟裂纹闭合积分法对应力强度因子进行了计算；张禹[59]在组合法的乘法式的基础上，拟合了几何修正系数方程来求解多裂纹结构的应力强度因子。

1.1.3边界元法计算应力强度因子

边界元法是与有限元法类似的另一种数值分析法，其控制方程为边界积分方程。对于某些三维孔边裂纹扩展问题，虽然可以采用有限元法求解，但是在划分网格、准备数据方面存在一定困难，而且需要花费大量的时间。由于边界元法具有降维的优势，可将三维问题转化为二维问题，大大减少了工作量。除此以外，边界元法是一种半解析半数值的方法，计算精度较高。

Newman[60-61]较早地利用边界元法对不同载荷情况下的无限宽板进行分析，得到了孔边两条等长裂纹的应力强度因子；巩建鸣等[62]研究了弯曲载荷作用下平板中孔单边角裂纹问题，采用边界元法得到了孔单边角裂纹的应力强度因子，并通过试验研究了在交变的弯矩作用下孔单边角裂纹的变化、扩展规律；雷钧等[63]采用时域边界元法，以矩形板中孔边裂纹的动态扩展问题为算例进行了裂纹快速扩展过程的数值模拟，并计算了应力强度因子。

虽然边界元法在降低维数、计算精度等方面优于有限元法，但是其由于自身局限性无法对非均匀介质问题进行求解，应用范围受到限制。对于一般非线性问题，边界元法的方程中产生的域内积分项，也会对边界元法求解应力强度因子的精确度造成影响。

1.2粒子滤波分析法

粒子滤波技术在非线性、非高斯系统中应用广泛。由于粒子滤波器具有多模态处理能力，所以在数据预测、跟踪、监控、定位中具有很大的优势。

Chen等[64]基于兰姆波粒子滤波器提出了一种疲劳裂纹扩展在线预测方法，通过主动兰姆波法对裂纹进行监测，采用有限元法建立了状态空间模型，实现了对孔边裂纹长度的评估；袁慎芳等[65]针对动态裂纹扩展问题，提出了一种基于动态裂纹数目的粒子滤波多裂纹扩展预测方法，当有新的裂纹萌生时，多裂纹扩展状态方程中相关参数进行更新，并根据裂纹扩展规律更新粒子集，实现了对结构中多裂纹的在线监测与预测；杨伟博等[66-67]提出了基于辅助粒子滤波的裂纹扩展寿命预测方法，通過PAIRS规则与压电主动LAMB波监测法分别建立状态方程与观测方程并构建模型，克服了上述方法过于依赖模型精确性的缺点，缓解了孔边裂纹监测多样性匮乏的现象。

基于粒子滤波的分析方法虽然在一定程度上解决了模型需要不断更新的问题，但是粒子滤波技术依然存在两个缺陷：一是随机样本过大时，容易导致计算量过大；二是随着计算、分析时间的延长，会产生粒子退化现象，降低效率。

2传感器实时监测

在孔边裂纹监测的众多方法中，除上述数据计算分析法以外，通过各种传感器对螺栓孔、铆接孔等部位的相关物理量进行监测、分析孔边损伤状况的方法也受到了广泛的研究。当螺栓孔或铆接孔发生孔边裂纹时，孔的内部结构会发生变化，导致孔周围的应力、应变随之发生变化。所以，通过监测孔边应力、应变的变化并加以分析就可以得到孔边裂纹的萌生以及扩展情况。在孔边裂纹无损检测技术中多采用射线、热辐射、数字图像等传感器进行孔边裂纹萌生、扩展的检测，而光纤传感器、声发射传感器、智能涂层传感器、薄膜传感器、应变片传感器以及涡流传感器实现了对孔边裂纹的实时监测。

2.1光纤传感器

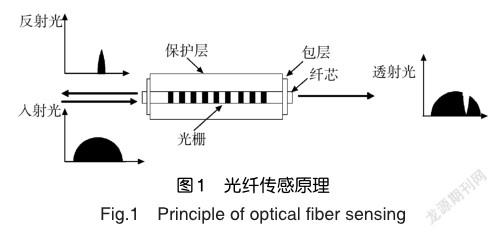
光纤传感器是一种新型传感器，光纤通信技术的不断发展促进了光纤传感器的产生。光纤传感器具有质量轻、体积小、耐高温、耐腐蚀、抗电磁干扰等[68]电类传感器所不具有优点，在飞机结构健康监测、大型土木建筑健康监测等领域应用广泛。在光纤传感系统中，宽带光源发出具有一定宽度的光，并通过光纤耦合器入射到光纤光栅中。入射光在光纤中传播受到光栅的波长选择性作用，符合条件的光会被反射回来。反射光再次经过光纤耦合器进入光纤解调仪中。当外界物理量发生变化时，会致使反射光的中心波长发生变化，光纤解调仪对反射光进行解调，就可以得到外界物理量的变化情况，光纤传感原理如图1所示。

Okabe等[69-70]在碳纤维增强复合材料层合板内部嵌入光纤布拉格光栅传感器，通过对测量光谱形状变化情况的分析以及数值模拟结果的对比，对含孔的碳纤维增强复合材料层合板孔边裂纹与分层损伤进行了监测；Shu等[71]在研究含螺栓接头的复合材料结构损伤时，将光纤沿螺栓孔嵌入结构内部，当螺栓孔出现孔边裂纹时会引起光纤应变的变化，从而实现监测；He等[72]基于高阶扩展有限元法与传输矩阵分析法等技术，提出了一种利用光纤布拉格光栅传感器进行概率裂纹尺寸量化的新框架，可根据光纤布拉格光栅传感器的反射强度谱对裂纹扩展情况进行监测并预测裂纹扩展趋势；张翰等[73]提出了一种基于横向布贴光纤光栅光谱图像分析的孔边裂纹诊断方法，利用有限元仿真软件ANSYS对预制孔以及预制孔边裂纹根据确定的试验条件进行有限元仿真分析，得到裂纹扩展到给定长度时应力在裂纹尖端附件区域的分布情况，并根据应力分布情况横向布置传感器感知裂纹尖端横向应力梯度的变化并反推光纤光栅传感器反射光谱的图像规律，通过试验加以验证后，得到反射谱次峰峰位置与裂纹扩展长度的关系，从而对孔边裂纹进行监测；张卫方等[74-75]对上述方案进行了改进，在纵向与横向均布置光纤光栅传感器以感知裂纹尖端的纵向和横向非均匀应变的变化，并对光纤光栅反射光谱图像进行了轴向应力仿真，得出了轴向应力三次方对光纤光栅影响最大，从而建立了光纤光栅反射光谱图像与裂纹扩展之间的关系，达到了孔边裂纹监测的目的。

以上学者所提出的光纤传感孔边裂纹监测方法，多依靠光谱图像信息对孔边裂纹进行监测。通过对光谱图像的分析判断裂纹扩展情况虽然形象直观，但是依然存在一些不足。首先，通过图像判断就意味着必须有图像显示设备，增加了系统的体积与质量，对于某些特殊场景就无法适用。其次，当遇到两种或多种不同的裂纹扩展引起相同的图像变化的情况时，裂纹监测就无法保证准确性，而且光谱图像的变化规律由反推获得，除系统误差外又引入了其他随机误差，这在一定程度上降低了孔边裂纹监测的精确度。

2.2声发射传感器

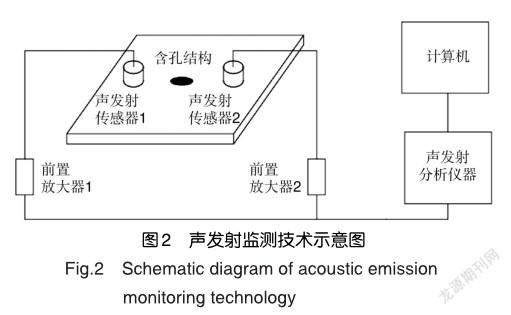
当结构产生裂纹萌生或扩展时，结构内部材料的应力和应变会发生变化而产生应变能。应变能在材料内部以波的形式传播时形成声发射信号，这些信号中包含了结构的损伤情况。声发射技术就是利用声发射传感系统中的换能器对来自被测结构内部的声发射信号进行收集，通过对声发射信号的特征参数的分析就可以对结构损伤进行判断。声发射传感器可以在一般传感器无法布置的部位进行监测，所以广泛应用于可达性较差的关键部位损伤监测中，声发射监测技术示意图如图2所示。

耿荣生等[76-77]在对飞机主梁裂纹进行监测时采用多参数识别与声发射技术对螺栓孔的孔边裂纹进行监测，耿荣生等[78-79]以此为基础，利用时间滤波、空间滤波、趋势分析等技术完成了对机翼连接区销钉孔孔边裂纹的监测；冯剑飞等[80-81]又对上述方法加以改进，加入了波形分析技术，实现了对螺栓孔孔边裂纹萌生的预报；刘文斌等[82]在耿荣生等所提出方法的基础上，用损伤区域内的事件数占总事件数的变化趋势分析孔边裂纹扩展情况，克服了传统空间滤波技术的不足；Hoang等[83]利用声发射技术与数字图像相关技术对含孔的铝合金薄板在承受拉伸载荷情况下的损伤机制进行了研究，声发射技术监测结构声学活动变化，数字图像相关技术监测结构应变场的变化，实现了对孔边裂纹的定位与识别；申雅峰等[84]在对含孔板进行孔边裂纹监测时，通过对三个阶段声发射信号的分析，实现了对裂纹萌生的预警以及扩展趋势的预测；王丹等[85]利用声发射信号特征参数与趋势分析法、关联分析法对铝合金板排钉的孔边裂纹进行监测，鉴别出了裂纹萌生与扩展的不同阶段；韩晖等[86]对声发射孔边裂纹监测试验进行了贝叶斯理论分析，对裂纹检测概率等参数进行了计算，为声发射监测技术的优化提供了支持；Bhuiyan等[87]将声发射监测技术与三维谐波有限元分析相结合对局部裂纹共振现象进行了研究，实现了飞机铝合金板孔边裂纹的监测；Bhuiyan等[88]又将声发射传感器与压电晶片有源传感器分别安装于含孔薄板的上下两侧，通过对声发射波形的分析，实现了孔边裂纹的监测；祁小凤等[89]针对随机载荷谱下耳片接头疲劳裂纹问题，采用定位分析与干扰排除分析对裂纹萌生与扩展情况进行了监测；黄华斌等[90]对飞机铆接壁板进行了监测，采用声发射参数滤波以及空间滤波、组合滤波等技术实现了强噪声环境下的孔边裂紋监测，为飞机壁板的疲劳损伤容限设计提供了便利。

声发射传感器既可以对金属结构进行监测又可以对复合材料等非金属结构进行监测，且监测覆盖面积广，不受被测结构几何形状的影响，可以在恶劣环境下进行监测。但是声发射监测技术容易受到噪声的干扰，在孔边裂纹监测中还会存在一些与裂纹无关的声发射信号，如配合件之间的摩擦等信号。虽然在上述学者的研究中，有部分方法实现了在噪声环境下对孔边裂纹的监测，但是大量的滤波技术不仅增加了工作量而且容易引入对孔边裂纹的误判所以如何在声发射监测技术中将噪声与无关信号剔除还需要进行深入研究。

2.3智能涂层传感器

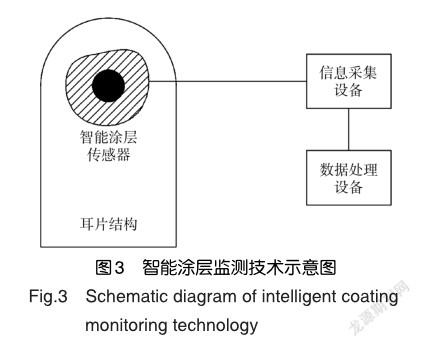
智能涂层传感器是一种可以黏附于待测结构关键部位表面的传感器。当被测结构表面出现裂纹时，智能涂层传感器中的损伤传感层会出现相应的裂纹，并随结构裂纹的扩展而扩展，引起损伤部位电位或电阻发生变化，通过对电位或电阻变化情况的分析就可以得到被测结构的损伤信息，智能涂层监测技术示意图如图3所示。

吕志刚等[91-92]发明了一种具有随附损伤特性的智能涂层，在使用时涂覆于铆钉孔或螺栓孔的孔边，其敏感末梢就可以反映孔边裂纹的萌生与扩展情况；杜金强等[93]对螺栓孔进行分析，结合电位法提出了一种涂覆于螺栓孔孔边的传感器，通过各监测点电位差的变化实现了对螺栓孔孔边裂纹的监测；Liu等[94]设计了一种可用于不同材料孔边裂纹监测的新型智能涂层传感器，实现了300μm以上裂纹的监测；侯波等[95]提出了一种表面涂层传感器克服了电位法的一些不足，实现了对多个关键位置的同时监测，但是承载能力与耐磨性仍需改进；白生宝等[96]对安装了智能涂层的含孔边裂纹的试件进行了疲劳试验，对智能涂层传感器监测孔边裂纹的适用性进行了验证；孙洋等[97]建立了智能涂层模型，研究了基体裂纹到达涂层界面后的穿越与偏转行为，对基体裂纹在界面的扩展行为进行了分析，为智能涂层传感器的优化设计奠定了基础；孙剑等[98]在对飞机短舱与吊挂的关键部位进行结构状态监测时，利用智能涂层对吊挂连杆试验件的连接孔的孔边裂纹进行了监测，完成了监测系统的软硬件集成化设计。

智能涂层传感器对电位、电阻信号等电信号的变化进行监测，所需要的信号处理算法比较简单可靠，功耗小。涂覆于结构表面的智能涂层可以实现全方位的孔边裂纹监测，不会受到方向的制约。而且目前的智能涂层传感器有很多采用防腐涂料制成，提高了传感器的使用寿命。智能涂层传感器的缺陷在于智能涂层的脆性较大，将其应用于复杂结构的健康监测时可能会由于某些因素的影响产生误报问题。而且智能涂层传感器涂覆于结构表面，还会存在脱落问题。

2.4薄膜传感器

薄膜传感器与智能涂层传感器工作原理类似，当待测结构表面出现裂纹时，薄膜传感器的电阻层会出现相应的裂纹，并随结构表面裂纹同步扩展，引起损伤部位电位、电阻发生变化，通过对电量变化的监测与分析实现对裂纹的监测。薄膜传感器与智能涂层传感器的不同之处在于薄膜传感器一般设计为环状或半圆形更加适合对螺栓孔、铆钉孔等难以接近部位的高精度损伤监测，相比于智能涂层传感器具有监测对象单一性的特点，薄膜传感器外观如图4所示。

侯波等[99-100]利用Ti/TiN薄膜传感器对飞机金属结构在服役中的裂纹进行实时监测，通过将Ti/TiN薄膜传感器与电位监测法相结合，实现了对铝合金板试件孔边裂纹的实时监测，侯波等[101]对Ti/TiN薄膜传感器进行了改进，设计了一种同心环状薄膜传感器，实现了对半圆孔孔边裂纹、任意角度孔边裂纹的实时监测，并且可以对孔边裂纹区域进行细分，得到裂纹损伤的径向尺寸；谭翔飞等[102]针对腐蚀环境下的孔边裂纹监测问题设计了一种铜薄膜传感器，监测精度达到了1mm；崔荣洪等[103]考虑了耦合服役环境下的孔边裂纹监测问题，经过大量试验，设计了一种稳定性与耐久性均较高的薄膜传感器，并将监测结果与显微镜结果进行了对比，二者信息基本一致；对于强化结构的孔边裂纹监测问题，刘凯等[104-105]对经过喷丸强化、孔挤压强化、激光冲击强化的结构分别进行了试验验证，得出薄膜传感器具有在高应力环境下对孔边裂纹进行监测的潜力。

薄膜传感器对金属结构自身的力学性能几乎不会有影响，具有较高的可靠性，适用于复杂环境下的裂纹监测。薄膜传感器的输出信号特征明显，不需要繁琐的信号处理过程。薄膜传感器中导电传感层的材料选择还需要进一步深入研究，导电传感层直接影响了薄膜传感器的随附损伤特性。薄膜传感器虽然具有很多传感器不具有的优势，但是薄膜传感器的制备要比其他传感器更加复杂，需要在结构表面制备薄膜，所以薄膜传感器只能在零部件装配前或操作空间较大的结构表面制备，对于某些已完成装配的空间狭小的部位监测则无能为力。

2.5应变片传感器

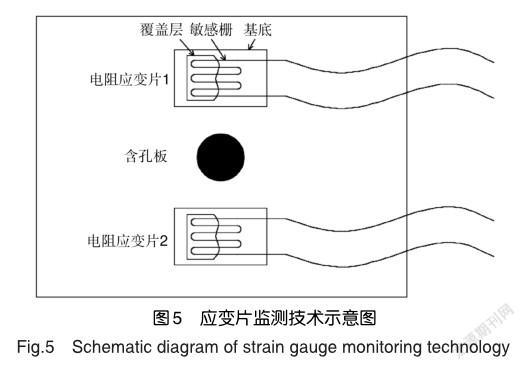
电阻应变片是最早用于结构健康监测的应变传感器，由于其安装简单的优势在土木、船舶、航空、航天等结构的健康监测中随处可见。电阻应变片的工作原理是金属的应变效应，即当被测结构发生损伤时，引起结构变形，粘贴结构表面的电阻应变片内的电阻丝阻值发生变化，通过对电阻阻值变化与应变的关系分析就可以得到结构的应变信息，应变片监测技术示意图如图5所示。

盖秉政等[106]在进行带孔板的冲击试验时利用电阻应变花进行了孔边裂纹的应变监测，并根据测得数据计算出了裂纹尖端的应力强度因子；安刚等[107]在对某型飞机进行全机疲劳试验时，提出了一种全机疲劳裂纹的应变片监测方法，通过应变片的监测数据可以提前发现裂纹；张永芳等[108]在进行机翼腹板疲劳试验时，采用应变花对高锁螺栓附近的裂纹进行了监测，并分析了裂纹产生的原因；刘洋[109]采用电阻应变片对处于腐蚀环境与交变载荷作用下的翼梁根部连接区孔边裂纹进行监测，得到了裂纹的扩展时间与形式等数据；王晓阳等[110]针对螺栓孔的孔边裂纹提出了一种应变差值监测法，以螺母或者螺栓头的圆心点为轴心在其周围均匀布置N个应变监测点，且两两对称设置。测量并记录应变监测点的应变数据，并将任意两两对称的应变监测点的应变数据差值与预定差值进行比较，当实际差值大于预定差值时判定有裂纹产生。

电阻应变片传感器安装方便，信号处理方式简单，测量范围比较广，而且通过对电路的简易设计就可以实现温度补偿，目前技术已经比较成熟。但是由于现在的大型机械结构越来越复杂，工作环境也各有不同，在一些强电磁干扰、高温、腐蚀等环境中，电阻应变片传感器极易受到干扰或损坏。同时，电阻应变片相对于其他种类的传感器体积略大，对于某些机械结构中可达性较差的部位无法进行监测，对于微小裂纹电阻应变片传感器也无法完成实时监测，这些缺陷都限制了电阻应变片在未来结构健康监测中的发展。

2.6涡流传感器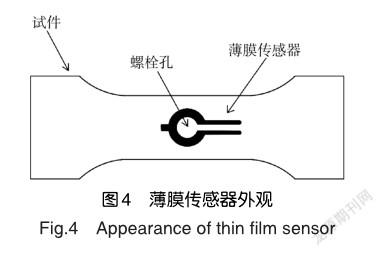

涡流传感器原本适用于结构损伤无损检测技术，通常设备较大，可完成零部件结构装配前或损伤发生后的检测。部分学者对涡流传感器进行了改进，开始将涡流传感器用于结构损伤监测。涡流传感器中的激励电流在被测空间产生激励磁场，通过涡流效应在金属结构的监测部位产生电涡流，从而产生感应磁场。当被测结构出现裂纹时，感应磁场会发生变化。通过分析磁场变化进而得到裂纹扩展的状况，涡流监测技术示意图如图6所示。

Zilberstein等[111]设计了一种称为弯曲绕组磁强计阵列的表面贴装涡流传感器，并通过拉伸疲劳试验，验证了其在“短裂纹”监测方面的实用性；Rakow等[112]利用涡流传感器膜研制了一种具有结构健康监测功能的螺栓，可实时监测金属结构螺栓孔边的疲劳裂纹；焦胜博等[113]设计了一种涡流阵列传感器，提出了针对孔边裂纹的监测方案，通过有限元仿真验证了监测方案的可行性，对传感器的定量监测能力进行了试验验证；丁华等[114]为完成螺栓孔孔边裂纹定量监测，设计了一种花萼状涡流阵列传感器，并进行了参数优化，监测精度达到了1mm；李培源等[115]设计了一种对不同材料具有不同最优监测频率的柔性涡流传感器，并对三种材料進行了试验，完成了对孔边裂纹的监测；樊祥洪等[116]设计了一种基于隧道磁阻传感器的柔性涡流传感器，不仅可以监测孔边表面裂纹，而且在施加激励频率的效果下还可以实现对2mm深裂纹的监测。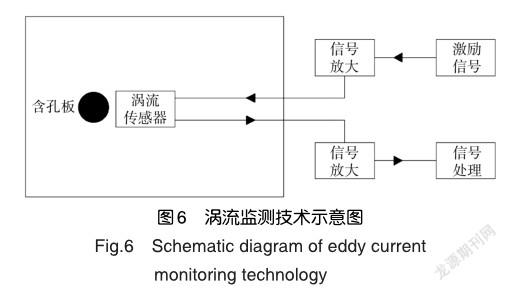

涡流传感器监测技术能够实现对被测结构的非接触监测，具有高分辨率与可靠性。涡流传感器可以穿透结构表面对结构内部损伤进行监测，不受油水等介质的影响。但是涡流传感器一般适用金属结构的监测，对于复合材料等无法产生感应磁场的材料并不适用，且涡流传感器容易受到电磁干扰，在对飞机、大型工业机械等进行损伤监测时要着重考虑干扰屏蔽措施，其应用受到了限制。由于技术暂不成熟，涡流传感器受温度影响很大，在温度超过70℃时传感器灵敏度就会降低甚至导致传感器损坏。

2.7多种传感器综合监测

多种传感器综合监测主要指利用两种或多种传感器对含孔结构的孔边裂纹进行监测，几种传感器优势互补，在不互相干扰的前提下实现对孔边裂纹的全面监测。张卫方等[117]将光纤应变花与智能涂层相结合进行孔边裂纹的监测，既可以测量多个方向的应力应变，又克服了智能涂层的高虚警率问题；孙磊[118]在进行复合材料孔边裂纹监测试验时，利用光纤传感器与压电传感器收集损伤信息，并结合卡尔曼滤波融合方法进行信息融合，不仅降低了误报发生，而且提高了定位精度。多种传感器综合监测是未来结构健康监测的发展重点，过去的文献多集中一种传感器的使用，虽然所使用的传感器体积越来越小，质量越来越轻，监测精度也在不断提高，但是依然存在很多缺陷。多种传感器综合使用虽然克服了许多传感器单独使用的不足，但是传感器种类过多必定会增大数据处理的工作量以及系统体积。所以多种传感器的集成化与小型化值得大力探索。表1对上述现有传感器监测技术的优缺点进行了简单总结。

从表1可以看出，应变片等技术较为成熟传统传感器在航空结构件孔边裂纹监测中的应用受到了很大的限制。而各种新型传感器，尤其是光纤传感器、智能涂层传感器、薄膜传感器由于自身优势在孔边裂纹监测方面具有很大的发展前景，但仍需加大研究力度，充分发挥其优势，弥补不足。

3结论及展望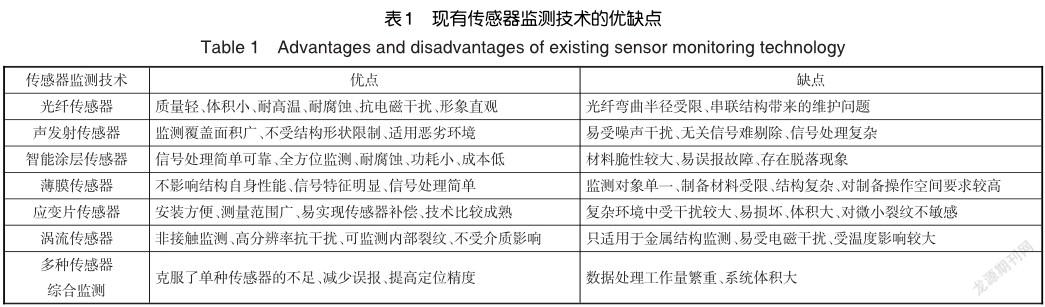

从20世纪50年代起，Bowie等就开始了对孔边裂纹的研究，并从最初的数学方法逐步发展到了如今的各种先进传感器监测方法。综合国内外对孔边裂纹监测技术的研究现状，认为孔边裂纹监测技术有以下几点值得继续深入研究：

（1）对于数据计算分析求应力强度因子、粒子滤波等方法，现有研究中的研究对象有椭圆孔、三角孔、无限大板等，所采用的计算、仿真方法也各有异同。因此，对于研究对象与研究方法的归纳整理以及规律总结是一项重要的工作。

（2）传感器监测法与数据计算分析法相比，目前的研究并不多。而且大多数采用了声发射传感器、电阻应变片传感器等较为成熟的传感器，而对于新型传感器，如光纤传感器、生物传感器等的应用较少。所以将新型传感器应用到孔边裂纹监测中是发展方向之一。

（3）航空、航天领域中的螺栓孔、铆接孔所处的环境复杂多变，对于某些特殊的场景需要特殊的传感器封装以及分析方法，所以根据不同的应用场景设计不同的传感器封装也值得深入研究。

（4）光纤传感器、智能涂层传感器、薄膜传感器等新型传感器的应用将会成为未来孔边裂纹监测技术的研究重点。若能将两种甚至多种先进传感技术与数据分析计算方法相融合，不仅可以提高对孔边裂纹监测的精确性，而且可以降低在监测过程中的虚警率。

（5）基于多传感器融合的同时，融合现有的数值计算分析法和大数据分析将是结构件孔边裂纹监测的新趋势。监测手段也将逐渐由离线监测发展为在线监测。未来，航空含孔关键结构的健康监测系统将会作为飞机故障诊断与健康管理系统的子系统，实现关键结构全生命周期的监测，在保障飞机飞行安全中发挥作用。

参考文献

[1]王善岭，罗建平.飞机表面用典型螺纹紧固件适配性研究[J].航空标准化与质量，2015（1）：7-11. Wang Shanling， Luo Jianping. Research on the adaptability of typical threaded fasteners for aircraft surfaces[J]. Aviation Standardization and Quality， 2015（1）：7-11. （in Chinese）

[2]方旭，薛景锋，宋昊，等.飞机结构健康监测系统数据处理及在线应用[J].计测技术，2019，39（6）：1-7. Fang Xu， Xue Jingfeng， Song Hao， et al. Data processing and online application of aircraft structure health monitoring system[J]. Measurement Technology， 2019， 39（6）：1-7. （in Chinese）

[3]缪宏，左敦稳，张敏，等.飞机起落架高强度钢内螺纹冷挤压成形金属流动规律研究[J].中国机械工程，2010，21（14）：1714- 1718. Miao Hong， Zuo Dunwen， Zhang Min， et al. Research on the metal flow law of cold extrusion forming of high-strength steel internal threads of aircraft landing gear[J]. China Mechanical Engineering， 2010， 21（14）： 1714-1818. （in Chinese）

[4]曲昌琦，周锐，杜宝，等.航空装备故障预测与健康管理的数据体系研究[J].航空科学技术，2020，31（12）：61-67. Qu Changqi， Zhou Rui， Du Bao， et al. Research on the data system of aviation equipment failure prediction and health management[J]. Aeronautical Science & Technology， 2020， 31（12）： 61-67. （in Chinese）

[5]王海峰.戰斗机故障预测与健康管理技术应用的思考[J].航空科学技术，2020，31（7）：3-11. Wang Haifeng. Thoughts on the application of fighter failure prediction and health management technology[J]. Aeronautical Science & Technology， 2020， 31（7）： 3-11. （in Chinese）

[6]赵猛，李聪，胡波，等.飞机线束上尾部附件的螺纹防松研究[C]//2020（第九届）民用飞机航电国际论坛，2020. Zhao Meng， Li Cong， Hu Bo， et al. Research on the anti-loose thread of the tail attachment on the aircraft wiring harness[C]// 2020 （Ninth） Civil Aircraft Avionics International Forum， 2020. （in Chinese）

[7]张彦军，王斌团，宁宇，等.飞机结构应变监控技术研究进展[J].航空科学技术，2020，31（7）：109-114. Zhang Yanjun， Wang Bintuan， Ning Yu， et al. Research progress of aircraft structural strain monitoring technology[J]. Aeronautical Science & Technology， 2020， 31（7）： 109-114.（in Chinese）

[8]Molent L. Fatigue crack growth from flaws in combat aircraft[J]. International Journal of Fatigue，2010，32（4）：639-649.

[9]高福亮.飛机复杂零件的超声检测分析与无损检测[J].中国新技术新产品，2018（10）：13-14. Gao Fuliang. Ultrasonic testing analysis and non-destructive testing of aircraft complex parts[J]. China New Technology and New Products， 2018（10）： 13-14. （in Chinese）

[10]彭智伟，姜跃进，王竹林.螺接结构孔边裂纹的超声原位检测[J].无损检测，2016，38（10）：67-71. Peng Zhiwei， Jiang Yuejin， Wang Zhulin. Ultrasonic in-situ detection of cracks on the edges of holes in screw joints[J]. Non-destructive Testing， 2016， 38（10）： 67-71. （in Chinese）

[11]田云飞，曹宗杰.红外检测在老龄飞机蒙皮搭接结构腐蚀检测中的应用分析[J].飞机设计，2013，33（3）：31-35. Tian Yunfei， Cao Zongjie. Application analysis of infrared detection in corrosion detection of lap joint structure of aging aircraft skin[J]. Aircraft Design， 2013， 33（3）： 31-35. （in Chinese）

[12]后雪冰，付跃文.飞机多层结构铆钉孔周缺陷的阵列脉冲涡流检测[J].无损检测，2018，40（10）：1-4. Hou Xuebing， Fu Yuewen. Array pulse eddy current detection of defects around rivet holes in aircraft multilayer structures[J]. Non-destructive Testing， 2018， 40（10）： 1-4.（in Chinese）

[13]雷美玲，付跃文.多层铆接结构铆钉孔周裂纹的脉冲涡流检测[J].失效分析与预防，2018，13（1）：13-18. Lei Meiling， Fu Yuewen. Pulse eddy current detection of cracks around rivet holes in multilayer riveting structures[J]. Failure Analysis and Prevention， 2018， 13（1）： 13-18. （in Chinese）

[14]刘秀丽.目视及X射线法检测裂纹概率曲线的测定[C]//第十二届全国结构工程学术会议，2003. Liu Xiuli. Determination of the probability curve of cracks detected by visual and X-ray methods[C]//The Twelfth National Academic Conference on Structural Engineering， 2003. （in Chinese）

[15]尤敬业，何娟娟.航空发动机叶片检测与裂纹分析[J].计测技术，2016，36（S1）：74-75. You Jingye， He Juanjuan. Aeroengine blade inspection and crack analysis[J]. Measurement Technology， 2016， 36（S1）： 74-75. （in Chinese）

[16]刘新辉.基于机器视觉的孔边缺陷检测算法研究与应用[D].深圳：深圳大学， 2015. Liu Xinhui. Research and application of hole edge defect detection algorithm based on machine vision[D]. Shenzhen： Shenzhen University， 2015. （in Chinese）

[17]周春阳，谢娜.基于机器视觉的外螺纹表面缺陷检测技术研究[J].科学技术创新，2019（28）：53-54. Zhou Chunyang， Xie Na. Research on surface defect detection technology of external thread based on machine vision[J]. Science and Technology Innovation， 2019（28）： 53-54. （in Chinese）

[18]Bowie O L.Analysis of an infinite plate containing radial cracks originating at the boundary of an internal circular hole[J]. Journal of Mathematical Physics，1956，35（1/4）：60-71.

[19]张永元，洪烈君.参奇性元在双孔边裂纹平板分析中的应用及其计算精度研究[J].应用力学学报，1986（3）：85-92. Zhang Yongyuan， Hong Liejun. The application of isoparametric singular element in the analysis of double-hole edge cracks and its calculation accuracy[J]. Chinese Journal of Applied Mechanics， 1986（3）： 85-92. （in Chinese）

[20]張永元，蔡皓东.多孔边裂纹板的应力强度因子计算[J].上海交通大学学报，1986（5）：77-86. Zhang Yongyuan， Cai Haodong. Calculation of stress intensity factors of cracked plates with porous edges[J]. Journal of Shanghai Jiaotong University， 1986（5）： 77-86.（in Chinese）

[21]赖俊彪，张行，何庆芝.含孔边裂纹有限大板的解析变分解法[J].航空学报，1990（9）：496-504. Lai Junbiao， Zhang Xing， He Qingzhi. Analytical variational method for finite large plates with hole edge cracks[J]. Acta Aeronautica et Astronautica Sinica， 1990（9）： 496-504. （in Chinese）

[22]傅东山，张行.含孔边裂纹有限大单块板的解析变分解法[J].航空学报，1992（11）：602-609. Fu Dongshan， Zhang Xing. Analytical variational decomposition method for a finite single plate with hole edge cracks[J]. Acta Aeronautica et Astronautica Sinica， 1992（11）：602-609. （in Chinese）

[23]赵晋芳，谢里阳，刘建中.共线多孔边对称裂纹板的应力强度因子计算[J].机械设计与制造， 2010（12）：12-14. Zhao Jinfang， Xie Liyang， Liu Jianzhong. Calculation of stress intensity factor of symmetrical cracked plate with collinear porous edges[J]. Mechanical Design and Manufacturing， 2010（12）： 12-14. （in Chinese）

[24]郭怀民，乔文华.椭圆孔边两不对称裂纹问题的复变函数解[J].力学季刊，2011，32（3）：444-451. Guo Huaimin， Qiao Wenhua. Solution of the problem of two asymmetric cracks on the edge of an elliptical hole with a complex variable function[J]. Quarterly Journal of Mechanics， 2011， 32（3）： 444-451. （in Chinese）

[25]Iida J，Hasebe N. Stress intensity factors of a rhombic hole with symmetric cracks under uniform transverse thin plate bending[J]. Engineering Fracture Mechanics，2016，156：16-24.

[26]吴学仁，黄新跃.受任意钉载圆孔边径向裂纹分析[J].航空学报，1988（9）：434-439. Wu Xueren， Huang Xinyue. Analysis of radial cracks on the edge of a circular hole subjected to arbitrary nailing[J]. Acta Aeronautica et Astronautica Sinica， 1988（9）： 434-439. （in Chinese）

[27]吴学仁.冷挤压孔边残余应力场中裂纹的应力强度因子[J].航空学报，1989（9）：442-447. Wu Xueren. Stress intensity factors of cracks in the residual stress field around the cold extrusion hole[J]. Acta Aeronautica Sinica， 1989（9）： 442-447. （in Chinese）

[28]吴学仁.有限板孔边裂纹的权函数解法[J].航空学报，1989

（12）：645-648. Wu Xueren. The method of weight function for the cracks on the edge of a finite plate[J]. Acta Aeronautica et Astronautica Sinica， 1989（12）：645-648. （in Chinese）

[29]宋大毅，張红玲，唐晨.受均匀内压作用的偏置孔边径向裂纹的应力强度因子[J].测试技术学报，1996（2）：550-553. Song Dayi， Zhang Hongling， Tang Chen. Stress intensity factors of radial cracks on the side of an offset hole subjected to uniform internal pressure[J]. Journal of Testing Technology， 1996（2）： 550-553. （in Chinese）

[30]谢伟，黄其青.椭圆孔边角裂纹应力强度因子的权函数求解方法[J].航空学报，2007（2）：328-331. Xie Wei， Huang Qiqing. The method of calculating the stress intensity factor of the corner crack of an elliptical hole[J]. Acta Aeronautica et Astronautica Sinica， 2007（2）： 328-331. （in Chinese）

[31]李政鸿，徐武，张晓晶，等.共线多孔两条不等长裂纹应力强度因子分析[C]//中国力学大会-2017暨庆祝中国力学学会成立60周年大会，2017. Li Zhenghong， Xu Wu， Zhang Xiaojing， et al. Stress intensity factor analysis of two collinear porous unequal length cracks[C]//Chinese Mechanics Conference-2017 and Celebration of the 60th Anniversary of the Founding of the Chinese Society of Mechanics， 2017. （in Chinese）

[32]李政鸿.多位置损伤平板的疲劳裂纹扩展试验与寿命预测方法研究[D].上海：上海交通大学，2018. Li Zhenghong. Research on fatigue crack growth test and life prediction method of multi-position damage flat plate[D]. Shanghai： Shanghai Jiaotong University， 2018. （in Chinese）

[33]李政鸿，徐武，张晓晶，等.多孔多裂纹平板的疲劳裂纹扩展试验与分析方法[J].航空学报，2018，39（7）：154-162. Li Zhenghong， Xu Wu， Zhang Xiaojing， et al. Fatigue crack growth test and analysis method of porous multi-crack flat plate[J]. Acta Aeronautica et Astronautica Sinica， 2018， 39（7）： 154-162. （in Chinese）

[34]童第华，吴学仁.应用权函数法计算孔边萌生裂纹的裂纹面位移[C]//第16届全国疲劳与断裂学术会议，2012. Tong Dihua， Wu Xueren. Using weight function method to calculate the crack surface displacement of the initiating crack at the edge of the hole [C]//The 16th National Conference on Fatigue and Fracture， 2012. （in Chinese）

[35]Tweed J，Rooke D P. The elastic problem for an infinite solid containing a circular hole with a pair of radial edge cracks of different lengths[J]. International Journal of Engineering Science，1976，14（10）：925-933.

[36]郭万林，肖寿庭.钉载孔边裂纹的应力强度因子[J].西北工业大学学报，1987（1）：129-136. Guo Wanlin， Xiao Shouting. Stress intensity factors of cracks on the edge of a nail loaded hole[J]. Journal of Northwestern Polytechnical University， 1987（1）： 129-136. （in Chinese）

[37]郭万林，傅祥炯.承载紧固孔边应力强度因子[J].航空学报， 1991（10）：507-510. Guo Wanlin， Fu Xiangjiong. Stress intensity factors of loadbearing fastening holes[J]. Acta Aeronautica et Astronautica Sinica， 1991（10）：507-510. （in Chinese）

[38]李新平，朱瑞赓.孔边线状裂纹断裂扩展的研究[J].岩土力学， 1988（1）：29-36. Li Xinping， Zhu Ruigeng. Research on the fracture propagation of linear cracks at the edge of a hole[J]. Rock and Soil Mechanics， 1988（1）： 29-36. （in Chinese）

[39]郭俊宏，盧子兴.无限大板中椭圆孔边快速传播裂纹的解析解[C]//中国力学学会学术大会，2009. GuoJunhong，LuZixing. Analyticalsolutionoffast propagating cracks on the edge of an elliptical hole in an infinite plate[C]//Chinese Society of Mechanics Academic Conference， 2009. （in Chinese）

[40]Santhanam S，Majerus J N，Jen K P，et al. Analytical/ numerical solutions for a single hole-edge crack in a narrow plate under pure bending[J]. Engineering fracture mechanics，1993，46（5）：751-761.

[41]Gong H，Jen K P，Majerus J N，et al. Analytical/numerical solutions for a single hole-edge crack in a wide plate under pure bending[J]. Engineering Fracture Mechanics，1993，46（5）：743-749.

[42]沈海军，郭万林.锪窝孔边扇形角裂纹应力强度因子的三维有限元分析[J].航空学报，2002（2）：106-110. Shen Haijun， Guo Wanlin. Three-dimensional finite element analysis of the stress intensity factor of the fan-shaped corner crack at the edge of the countersink hole[J]. Acta Aeronautica etAstronautica Sinica， 2002（2）： 106-110. （in Chinese）

[43]王立清.工程中含接触问题的孔边裂纹应力强度因子数值研究[D].哈尔滨：哈尔滨工业大学，2009. Wang Liqing. Numerical study on stress intensity factor of hole edge cracks with contact problems in engineering[D]. Harbin： Harbin Institute of Technology， 2009. （in Chinese）

[44]江勇.航空连接结构的三维应力集中与裂纹分析[D].南京：南京航空航天大学，2009. Jiang Yong. Three-dimensional stress concentration and crack analysis of aviation connection structure[D]. Nanjing： Nanjing University ofAeronautics andAstronautics， 2009. （in Chinese）

[45]王艾伦.干涉装配孔边角裂纹应力强度因子计算[J].江苏航空，2012（S1）：93-95. Wang Ailun. Calculation of stress intensity factor for corner cracks of interference assembly holes[J]. Jiangsu Aviation， 2012（S1）： 93-95. （in Chinese）

[46]龚德志，李亚智，王海.紧固件孔边三维疲劳裂纹扩展研究[J].机械强度，2012，34（6）：868-874. Gong Dezhi， Li Yazhi， Wang Hai. Three-dimensional fatigue crack growth of fastener holes[J]. Mechanical Strength， 2012， 34（6）： 868-874. （in Chinese）

[47]王海，束一秀，李亚智.带锪窝紧固件孔边三维多裂纹扩展的计算分析[J].航空工程进展，2013，4（2）：175-181. Wang Hai， Shu Yixiu， Li Yazhi. Computational analysis of three-dimensional multi-crack propagation at the edge of a fastenerwithcountersinks[J]. Advancesin Aeronautical Engineering， 2013， 4（2）： 175-181. （in Chinese）

[48]Stern M，Becker E B，Dunham R S. A contour integral computation of mixed-mode stress intensity factors[J]. Inter- national Journal of Fracture，1976，12（3）：359-368.

[49]Dolbow J，Moran B. Domain integral formulation for stress intensity facto computation along curved three dimensional interfacecracks[J]. InternationalJournalofSolidsand Structures，1998，35（15）：1763-1783.

[50]郁大照，陈跃良，郁章艳，等.含MSD共线多孔平板应力强度因子有限元分析[J].海军航空工程学院学报，2006（5）： 561-565. Yu Dazhao， Chen Yueliang， Yu Zhangyan， et al. Finite element analysis of stress intensity factors of collinear porous plates containing MSD[J]. Journal of Naval Aeronautical Engineering Institute， 2006（5）： 561-565.

[51]张文东，董登科.共线多孔MSD的干涉影响及裂纹扩展模拟[J].机械强度，2013，35（6）：829-833. Zhang Wendong， Dong Dengke. Interference influence and crack propagation simulation of collinear porous MSD[J]. Mechanical Strength， 2013， 35（6）： 829-833. （in Chinese）

[52]云双，李弢.機身蒙皮孔边裂纹修理的损伤容限评定[J].航空科学技术，2016，27（7）：21-25. Yun Shuang， Li Tao. Damage tolerance assessment for the repair of the hole edge cracks in the fuselage skin[J]. Aeronautical Science & Technology， 2016， 27（7）： 21-25. （in Chinese）

[53]孙晓娜，贺小帆，李玉海.孔边倒角裂纹当量初始缺陷尺寸的确定方法[J].北京航空航天大学学报，2018，44（1）：187-195. Sun Xiaona， He Xiaofan， Li Yuhai. The method for determining the equivalent initial defect size of the hole edge chamferingcrack[J].JournalofBeijingUniversityof Aeronautics and Astronautics， 2018， 44（1）： 187-195. （in Chinese）

[54]李岩，冯永志，杜伟.孔边缘单侧裂纹应力强度因子计算方法[J].科学技术创新，2019（8）：5-6. Li Yan， Feng Yongzhi， Du Wei. Calculation method of stress intensity factor for unilateral cracks at the edge of hole[J]. Science and Technology Innovation， 2019（8）： 5-6. （in Chinese）

[55]吴庆涛，龙江.基于ABAQUS/Franc3D的孔边疲劳裂纹扩展分析[J].西安航空学院学报，2020，38（3）：11-16. Wu Qingtao， Long Jiang. Analysis of fatigue crack propagation at the edge of a hole based on ABAQUS/Franc3D[J]. Journal of Xian Aeronautical University， 2020， 38（3）： 11-16. （in Chinese）

[56]邹君，张悦超，冯振宇，等.含多部位损伤搭接结构应力强度因子三维有限元分析[J].南京航空航天大学学报，2020，52（4）： 618-623. Zou Jun， Zhang Yuechao， Feng Zhenyu， et al. Threedimensional finite element analysis of stress intensity factors of lapped structures with multiple damages[J]. Journal of Nanjing University of Aeronautics and Astronautics， 2020， 52（4）：618-623. （in Chinese）

[57]孙益军.多部位损伤结构的疲劳寿命预测[D].南京：南京航空航天大学， 2008. Sun Yijun. Fatigue life prediction of multi-part damage structure[D]. Nanjing： Nanjing University of Aeronautics and Astronautics， 2008. （in Chinese）

[58]Zhao J F，Zhao Q. Typical calculation method of stress intensity factors and crack growth criterions on infinite plate containing hole-edge cracks[J]. Advanced Materials Research，2012，568：154-158.

[59]张禹.孔边多裂纹结构的裂纹扩展寿命研究[D].北京：北京理工大学，2016. Zhang Yu. Research on crack propagation life of multi-crack structures around holes[D]. Beijing： Beijing Institute of Technology， 2016. （in Chinese）

[60]Newman J C. An improved method of collocation for the stress analysis of cracked plates with various shaped boundaries[R]. NationalAeronautics and SpaceAdministration，1971.

[61]Newman J C. A nonlinear fracture mechanics approach to the growth of small cracks[R]. National Aeronautics and Space Administration Hampton va Langley Research Center，1983.

[62]巩建鸣，沈士明，戴树和.弯曲载荷作用下孔边角裂纹的应力强度因子与疲劳扩展规律[J].南京工业大学学报（自然科学版），1990（3）：51-57. Gong Jianming， Shen Shiming， Dai Shuhe. Stress intensity factor and fatigue growth law of hole corner cracks under bending load[J]. Journal of Nanjing University of Technology（Natural Science Edition）， 1990（3）： 51-57. （in Chinese）

[63]雷钧，黄祎丰，杨庆生.裂纹动态扩展的边界元模拟[J].北京工业大学学报，2013，39（6）：806-810. Lei Jun， Huang Yifeng， Yang Qingsheng. Boundary element simulation of crack dynamic growth[J]. Journal of Beijing University of Technology， 2013， 39（6）： 806-810. （in Chinese）

[64]Chen J，Yuan S，Qiu L，et al. Research on a Lamb wave and particle filter-based on-line crack propagation prognosis method[J]. Sensors，2016，16（3）：320.

[65]袁慎芳，陈健，邱雷，等.基于动态裂纹数目的粒子滤波多裂纹扩展预测方法， CN109345032A[P]. 2019-02-15. Yuan Shenfang， Chen Jian， Qiu Lei， et al. Particle filter multicrack propagation prediction method based on the number of dynamic cracks， CN109345032A[P]. 2019-02-15. （in Chinese）

[66]杨伟博.基于在线监测和粒子滤波的裂纹扩展预测方法[D].南京：南京航空航天大学， 2017. Yang Weibo. Crack growth prediction method based on online monitoring and particle filter[D]. Nanjing： Nanjing University ofAeronautics andAstronautics， 2017. （in Chinese）

[67]楊伟博，袁慎芳，邱雷，等.基于辅助粒子滤波的疲劳裂纹扩展预测研究[J].振动与冲击，2018，37（5）：114-119， 125. Yang Weibo， Yuan Shenfang， Qiu Lei， et al. Research on fatigue crack growth prediction based on auxiliary particle filter[J]. Vibration and Shock， 2018， 37（5）： 114-119， 125. （in Chinese）

[68]陈璐，宋昊，李新良，等.OpenGL在FBG传感网络结构健康监测中的应用[J].计测技术，2008（5）：51-53， 57. Chen Lu， Song Hao， Li Xinliang， et al. Application of OpenGL in FBG sensor network structure health monitoring[J]. Measurement Technology， 2008（5）： 51- 53， 57. （in Chinese）

[69]Okabe T，Yashiro S. Damage detection in holed composite laminates using an embedded FBG sensor[J]. Composites Part A，2012，43（3）：388-397.

[70]Yashiro S，Okabe T. Estimation of fatigue damage in holed composite laminates using an embedded FBG sensor[J]. Composites PartA，2011，42（12）：1962-1969.

[71]Shu M，Takeda N. Recent advancement in optical fiber sensing for aerospace composite structures[J]. Photonic Sensors，2013，3（4）：345-354.

[72]He J，Yang J，Wang Y，et al. Probabilistic model updating for sizing of hole-edge crack using fiber bragg grating sensors and the high-order extended finite element method[J]. Sensors，2016，16（11）：1-22.

[73]张翰，金博，张萌.一种基于横向布贴光纤光栅光谱图像分析的孔边裂纹诊断方法，CN106767475B[P]. 2019-10-18.Zhang Han， Jin Bo， Zhang Meng. A method for diagnosing hole edge cracks based on spectral image analysis of laterally clothed fiber gratings， CN106767475B[P]. 2019-10-18. （in Chinese）

[74]张卫方，张萌，金博，等.一种基于光纤光谱图像分析的孔边裂纹诊断方法， CN106596255A[P].2017-04-26. Zhang Weifang， Zhang Meng， Jin Bo， et al. A method of hole edge crack diagnosis based on optical fiber spectral image analysis， CN106596255A[P]. 2017-04-26. （in Chinese）

[75]張卫方，金博，张萌，等.一种基于两种布贴方式下光纤光栅光谱图像分析的孔边裂纹诊断方法，CN106840869B[P].2019-08-23. Zhang Weifang， Jin Bo， Zhang Meng， et al. A method for hole edge crack diagnosis based on fiber grating spectral image analysis under two types of placement methods，CN106840869B[P]. 2019-08-23. （in Chinese）

[76]耿荣生，景鹏，雷洪，等.飞