金属材料重复冲击拉伸试验方法研究

钱诚成 白春玉 杨强 杨素淞 王标 胡伟平 詹志新

摘要：为研究航空典型金属材料的重复冲击拉伸力学性能，自主设计加工了一套重复冲击拉伸试验装置，在Instron 9350型落锤冲击试验机上实现了圆棒状TC18钛合金试件的重复冲击拉伸加载试验。试验测试得到TC18钛合金试件在不同冲击能量加载下的冲击载荷—时间历程和冲击次数。建立了冲击拉伸过程的有限元计算模型，分别采用按冲击速度加载和按冲击载荷—时间历程加载两种方式，计算了试件轴力—时间历程以及等效塑性应变—时间历程。冲击载荷—时间历程曲线的重复性，以及数值计算中锤头速度—时间历程结果表明了试验方法的可行性和适用性。两种加载方式下等效塑性应变-时间历程对比为后续进一步建立合适的重复冲击数值计算模型提供了重要参考依据。

关键词：重复冲击拉伸；试验装置；落锤冲击试验机；TC18钛合金；冲击载荷

中图分类号：V215.5+2文献标识码：ADOI：10.19452/j.issn1007-5453.2021.12.011

基金項目：航空科学基金（20184151017，202041051001）

承受重复冲击载荷作用的结构件在工程应用中广泛存在，如航母舰载机的拦阻钩、枪械上的撞针、钻机的牙轮等[1]。这些结构件在多次冲击载荷作用下，薄弱位置逐渐发生损伤并累积，经过一定次数冲击后产生裂纹并扩展至断裂[2]，往往会酿成重大安全事故，造成较大的经济损失。有研究表明，材料的冲击疲劳性能与经常规疲劳性能存在较大差异，材料的变形规律、疲劳强度、裂纹萌生特性、裂纹扩展特性均存在差异[3]。因此，研究这些受重复冲击载荷作用结构件的疲劳损伤机理、损伤累积规律、疲劳寿命影响因素等对抗冲击疲劳工程结构设计优化和冲击疲劳寿命预估具有重大意义[4]。试验研究是进行理论研究的重要基础，目前国内外研制的冲击试验机大多为摆锤式或落锤式试验机，其基本原理是利用自由落体的速度对试验件实现冲击加载，通过调整释放高度以及释放重物的质量，达到预期的撞击速度或者撞击能量[5]。现有的重复冲击动力学问题研究的大多是冲击压缩与冲击弯曲问题，通过现有冲击试验机比较容易实现这两种形式的加载，如Sun等[6]在研究AerMet100钢冲击疲劳性能时，采取的试验方法为缺口梁的冲击三点弯曲；Gao等[7]在研究缺口试验件低速冲击疲劳寿命时，采取的试验方法为悬臂梁冲击弯曲；赵凯等[8]在研究冲击载荷下弹簧钢的多轴疲劳行为时，采取电液伺服材料试验机施加拉-扭冲击载荷。

然而，在相当一部分的工程实际应用中，结构件常常承受重复冲击拉伸载荷作用，如航空母舰载机在着舰过程中其拦阻钩的受力状态[9]。不少金属材料的拉伸和压缩力学性能存在一定的差异性[5]，这会导致它们的冲击疲劳寿命也有所不同。对于这一类问题的研究，在试验方面实现对金属试件的冲击拉伸加载具有重要意义，也将为后续全面研究金属材料的冲击疲劳性能奠定基础。本文设计加工了一套冲击拉伸试验装置，在Instron 9350型落锤冲击试验机上实现了圆棒状TC18钛合金试件的重复冲击拉伸加载，采集到不同冲击能量下的冲击载荷时间历程。然后建立了模拟冲击拉伸过程的有限元模型，并分别采用按冲击速度和按冲击载荷—时间历程两种加载方式，计算了试件的轴力—时间历程，表明了试验方案的可行性与适用性。

1试验方案设计

1.1试验目的

本文为了测试金属材料重复冲击力学性能，以及冲击疲劳寿命制订了一套重复冲击拉伸试验方案，其主要目的是通过试验数据验证试验方案的可行性，为后续深入研究金属材料冲击疲劳问题提供试验基础。

本文中重复冲击拉伸试验是在Instron 9350型落锤冲击试验机上完成的，试验机如图1所示。该试验机的冲击能量范围为0.59～1800J，模拟冲击速度范围为0.75～24m/s。试验机由移动控制系统、定位装置、升降装置、防回弹装置、捕捉装置、缓冲装置、载物台组成。试验系统具备冲击载荷数据采集、曲线绘制、报告编辑等功能。

1.2冲击拉伸试验装置设计

根据试验机的接口信息设计了如图2所示的冲击拉伸疲劳试验装置，将锤头自由落体运动产生的冲击载荷转化为对试件的冲击拉伸载荷。整个试验装置由锤头、连接盖板、支座、下夹头、底座、连接螺钉、限位压条、固定螺钉、棒状试验件和锁紧螺母组成。

支座设计如图3所示，内部为圆柱体空腔，两侧开有对称矩形引导槽，顶部中心为？10圆形通孔，底部有定位凹槽；下夹头如图4所示，圆盘中心为M10螺纹通孔，圆盘两侧为伸出的凸台砧座。

试验件安装步骤：（1）试验装置底座通过螺栓和试验机载物台固定连接，将试验机的锤头更换为图2中的锤头；（2）圆棒试验件下夹持段通过螺纹以及双螺母与下夹头固定锁紧；（3）圆棒试验件上夹持段穿过支座的顶部中心圆孔，通过双螺母与支座锁紧固定，下夹头位于支座的内部空腔中，装配后确保下夹头两侧凸台不与支座引导槽接触；（4）连接盖板通过连接螺钉与下夹头的两侧凸台连接；（5）支座通过底部定位凹槽与底座上的定位凸台对接来定位，再通过压条、螺钉将支座固定在底座上。冲击拉伸试验装置装配完成后的状态如图5所示。在落锤冲击试验过程中，锤头施加在试验装置上的冲击载荷通过下夹头传递给试验件，实现对试验件的冲击拉伸加载。

1.3试验件设计

本文试验件采用的材料是TC18钛合金，是一种高强度、耐腐蚀的α-β两相合金，同时具有塑性低、导热系数低等特点，被广泛应用航空航天、船舶和武器工业[10]。TC18钛合金的主要化学成分见表1，静态力学性能参数见表2。

应变率的大小不仅取决于加载速度的大小，还取决于试验件的尺寸。相同加载速度下，试验件的尺寸越小，其变形的应变率就越大。因此在设计冲击拉伸试验件时，试验段的尺寸不宜过大。最终设计的试验件在冲击能量6～30J的范围内，应变率能达到50～200s-1。

冲击拉伸试验件几何尺寸如图6所示，两端夹持段为螺纹段，中间试验段长5mm，截面直径5mm。

根据试验机的试验条件和试验测试目标，选取一种典型工况（冲击能量约20J）进行单次冲击模拟。试验件中心处单元的应变—时间曲线如图7所示，加载段的平均應变率达到了150s-1，处于低速动态范围，试验件尺寸设计合理。

2试验结果分析

2.1试验结果

为了获得不同高应变率下试件的冲击响应与冲击寿命，一共进行了4个能量级别的重复冲击试验。试验结果见表3，断裂失效后的试验件如图8所示。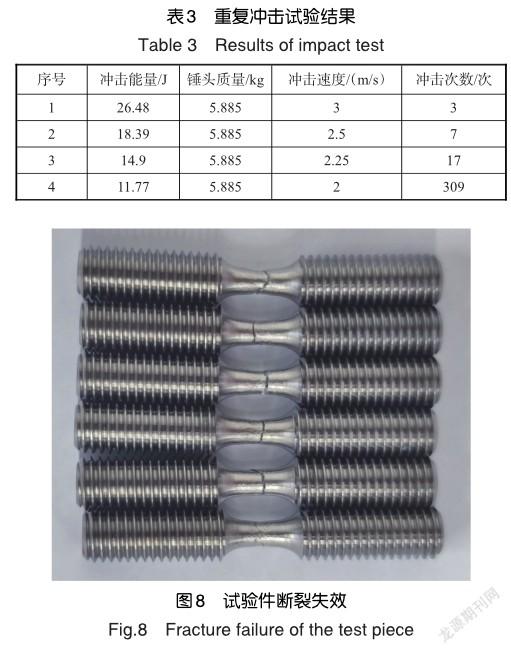

1号试验件3次冲击过程的载荷—时间历程如图9（a）所示；2号试验件7次冲击过程的载荷—时间历程如图9（b）所示；3号试验件的部分冲击载荷—时间历程如图9（c）所示；4号试验件的部分冲击载荷—时间历程如图9（d）所示。由图9可以看出，相同冲击能量下，除最后一次冲击过程，前面的冲击过程载荷—时间历程重复性很好。

2.2试验数据处理

在首次冲击过程中，锤头的速度—时间关系、位移—时间关系分别如图10、图11所示。

为了对比按冲击速度和按冲击载荷—时间历程两种加载方式下试验件的力学响应，并且由试验数据可知，试验件冲击破坏之前，每次冲击的载荷—时间曲线差别并不明显，故将前N-1次的冲击载荷—时间历程的均值作为代表性冲击载荷曲线，用以计算试验件的冲击响应。需要说明的是，这种处理方法没有考虑材料损伤对冲击响应的影响，仅仅是通过一种数据处理方法得到代表性冲击载荷曲线，便于数值计算。

但在实际数值计算中，若按传感器测得的载荷—时间历程加载，由于加载曲线抖动剧烈，会严重影响计算效率，尤其当进行重复冲击加载计算时。因此，对取均值之后的冲击载荷—时间数据进行滤波处理，得到更为光顺的冲击载荷—时间历程曲线，如图12所示。

3冲击过程的数值模拟

3.1按冲击载荷—时间历程加载数值计算

将以试验机传感器测得的载荷—时间历程为基础并进行平均化和滤波处理后的载荷—时间曲线作为载荷条件，并采用如图13所示有限元计算模型。在该模型中不存在锤头。另外，考虑到冲击过程的计算较为复杂，为提高计算效率，首先对模型做出以下简化：（1）假设连接盖板为刚体，外载荷直接施加在盖板中心处；（2）通过对试验件上夹持段固定约束（边界条件）替代支座；（3）试验件下夹持段与下夹头绑定，下夹头与连接盖板绑定。网格划分采用C3D8R单元，最小单元尺寸约为0.4mm×0.4mm×0.2mm。

采用ABAQUS软件显式动力求解器进行数值模拟，试验件的应力应变本构关系参见式（4），其硬化模式为各向同性硬化，塑性应变增量遵循正则流动法则[13]。

3.1.1单次冲击的计算结果

4次数值模拟冲击得到的试验件轴力—时间历程如图14所示，与输入载荷（见图12）相比，波形变化趋势一致。图15对比了冲击速度为2.5m/s时对应的输入载荷和试件轴力时间历程，曲线整体右移，数值大于输入载荷。这是由于有限元计算采用的显示动力学方法，考虑了惯性力的影响以及冲击响应效应，因此试件中心截面的轴力与输入载荷并不同步，且数值大小也有所差别。

3.1.2多次冲击的计算结果

各种载荷条件下重复加载时试件试验段平均等效塑性应变累积过程如图16所示。从图16可以看出，随着冲击速度的增加，单次冲击时的试验段的平均等效塑性应变增量也增加。但是累计等效塑性应变与每种冲击速度下的总冲击次数有关，这部分计算结果还需要进一步的试验测试来验证。

3.2按冲击速度加载数值计算

本节在前述建立的冲击拉伸模拟的有限元模型基础上，改变加载方式，将盖板设定为弹性体，锤头简化为刚体，通过在锤头上施加速度载荷，计算试样的冲击响应，并与采用载荷—时间曲线的加载方式进行对比，为建立冲击过程模拟的数值计算方法提供重要的参考依据。计算模型如图17所示。对锤头除竖直方向外的其他自由度进行约束，试件单元类型为C3D8R单元，最小单元尺寸约为0.4mm× 0.4mm×0.2mm。

3.2.1单次冲击的计算结果

圖18、图19分别展示了单次冲击过程中锤头的速度变化曲线和位移变化曲线。从速度—时间曲线来看，4种初始冲击速度加载情况下，锤头反弹后脱离接触的速度相近，约为1m/s，这与2.2节的积分结果比较吻合。数值模拟中锤头位移与2.2节积分结果的差异可归结为数值计算模型与实际试验的差异。另外，试验采用的TC18钛合金试验件的动态本构借鉴的参考文献[12]中的结果，可能与试验所用试件材料因加工工艺、表面处理方式不同而本构关系有所不同，这也会造成锤头位移的差异。但不同速度级别的冲击过程中，锤头位移的相对变化趋势与2.2节积分结果一致。

不同冲击速度下试件的轴力—时间曲线如图20所示，V=2.5m/s时的轴力—时间历程与图14对比，如图21所示。两种加载方式下的试件中心截面轴力—时间历程相似，数值大小近似，但按载荷—时间历程加载时，试件轴力—时间历程曲线相对速度加载情况下整体右移，冲击载荷传播速度略小于按冲击速度加载方式时的情况。

3.2.2多次冲击的计算结果

图22为试件试验段平均等效塑性应变—时间历程曲线，与图16相比，相同次数冲击加载下，按冲击速度加载时试件试验段平均等效塑性应变偏大。其原因可归结为：按速度加载时数值模型与实际情况的差别的影响。如模型中落锤冲击过程无摩擦、无阻尼；模型中试件上夹持段设置完全刚性边界条件；锤头简化为刚体；并对除Z方向外的其他位移进行约束；冲击位置与实际试验相比过于精确。这些因素都会导致数值模拟过程的冲击载荷大于实际冲击载荷。

按照冲击载荷—时间历程加载的数值方法首先需要获取冲击载荷谱，这对于构件的冲击疲劳性能预测来说存在困难。但按冲击速度加载方式得到的计算结果偏大。通过两种加载方式计算结果的对比，再结合后续试验应变的测量，对按速度冲击加载方式数值计算模型进行修正（如数值模型中加入阻尼），则是建立合适的重复冲击数值计算模型的可行之法。

4结论

本文为研究典型航空材料的冲击疲劳性能，设计了一套冲击拉伸疲劳试验装置，并将该装置应用于Instron 9350型落锤试验机上，验证了所设计试验装置和试验方法的可行性。通过不同冲击能量下圆棒试件的重复冲击拉伸试验，得到了对应的重复冲击次数，以及每次冲击时的载荷—时间历程，进一步验证了试验装置的稳定性。再进一步建立了试件重复冲击过程模拟的有限元模型，计算了按冲击载荷—时间历程和按冲击速度两种加载方式下的冲击响应，得到的试验件的轴力—时间历程基本相似，但按冲击速度加载时得到的试样轴力要略大，而且载荷传播速度也略快。该计算结果为后续进一步建立合适的重复冲击数值计算模型提供了重要参考依据。

参考文献

[1]王学颜，宋广惠.结构疲劳强度设计与失效分析[M].北京：兵器工业出版社，1992. Wang Xueyan， Song Guanghui. Structural fatigue strength design and failure analysis[M]. Beijing： Ordnance Industry Press，1992.（in Chinese）

[2]郭玉佩，王彬文，杨强，等.航空材料的冲击疲劳问题研究进展与展望[J].航空工程进展， 2020，11（5）：1-9. Guo Yupei， Wang Binwen， Yang Qiang， et al. Research progress and prospect of impact fatigue of aeronautical materials[J]. Progress in Aeronautical Engineering， 2020，11（5）： 1-9.（in Chinese）

[3]杨素淞，白春玉，杨强，等.金属材料与结构冲击疲劳问题研究综述[J].航空科学技术，2021，32（2）：1-13. Yang Susong， Bai Chunyu， Yang Qiang， et al. Review on impactfatigueofmetalmaterialsandstructures[J]. Aeronautical Science & Technology， 2021， 32（2）： 1-13.（in Chinese）

[4]刘小川，王彬文，白春玉，等.航空结构冲击动力学技术的发展与展望[J].航空科学技术，2020，31（3）：1-14. Liu Xiaochuan， Wang Binwen， Bai Chunyu， et al. Progress and prospect of aviation structure impact dynamics[J]. Aeronautical Science & Technology， 2020，31（3）：1-14.（in Chinese）

[5]余同希，邱信明.冲击动力学[M].北京：清华大学出版社，2011. Yu Tongxi， Qiu Xinming. Impact dynamics[M]. Beijing： Tsinghua University Press， 2011.（in Chinese）

[6]Sun Q，Liu X R，Liang K. Impact fatigue life prediction for notched specimen of steel AerMet100 subjected to high strain rate loading[J]. International Journal of Applied Mechanics，2018：S1758825118500308.

[7]Gao D Y，Yao W X，Wen W D，et al. Critical distance model for the fatigue life analysis under low-velocity impacts of notched specimens[J]. International Journal of Fatigue，2021，146：106164.

[8]趙凯，何玉怀，刘新灵，等.冲击载荷下50CrVA弹簧钢的多轴疲劳行为研究[J].航空科学技术，2014，25（7）：68-72. Zhao Kai， He Yuhuai， Liu Xinling， et al. Multiaxial fatigue behavior of 50CrVA spring steel under impact loading[J]. Aeronautical Science & Technology， 2014， 25（7）： 68-72.（in Chinese）

[9]杨全伟.舰载飞机拦阻钩载荷实测方法研究[J].航空学报， 2014， 36（4）： 1162-1168. Yang Quanwei. Research on measurement method of arresting hook load of carrier-based aircraft[J]. Acta Aeronautica et Astronautica Sinica， 2014， 36（4）： 1162-1168.（in Chinese）

[10]Boyer R R. An overview on the use of titanium in the aerospace industry[J]. Materials Science and Engineering：A，1996，213：103-114.

[11]Chen X，Soveja A，Chaussumier M，et al. Effect of MEVVA ion implantation on fatigue properties of TC18 titanium alloy[J]. Surface and Coatings Technology，2018，344，：572-578.

[12]Zhang C M，Mu A，Wang Y，et al. Study on dynamic mechanical properties and constitutive model construction of TC18 titanium alloy[J]. Metals，2020，10（1）：44.

[13]王勖成.有限单元法[M].北京：清华大学出版社，2003. Wang Xucheng. Finite element method[M]. Beijing： Tsinghua University Press，2003.（in Chinese）

Research on Repeated Impact Tensile Test Method for Metallic Materials

Qian Chengcheng1，Bai Chunyu2，Yang Qiang2，Yang Susong1，Wang Biao1，Hu Weiping1，Zhan Zhixin1

1. Beihang University，Beijing 100191，China

2. Aviation Key Laboratory of Technology and Science on Structure Impact Dynamics，AVIC Aircraft Strength Research Institute，Xian 710065，China

Abstract： In order to study the mechanical properties of typical aeronautical metal materials by repeated impact tensile test， a set of special jig for repeated impact tensile test is self-designed and manufactured. The repeated impact tensile test of TC18 titanium alloy specimen with round shape is carried out on Instron 9350 type drop hammer impact test machine. The impact load-time histories and impact times of TC18 titanium alloy specimens under different impact energy loading are obtained. The finite element model of impact tensile process is established， and the axial force-time histories and the equivalent plastic strain-time histories of the specimens are calculated by the impact velocity loadings and the impact load-time histories respectively. The repeatability of the impact load-time history curves and the computed velocity-time histories of the hammer verifies the feasibility and applicability of the test method. The comparison between equivalent plastic strain-time histories under the two loading modes provides important references for the further establishment of appropriate numerical calculation model of repeated impact.

Key Words： repeated impact tensile； special jig of test； drop hammer impact test machine； TC18 titanium alloy； impact load