使用移测显微镜测量平行平板的折射率

范海英，贾小文，贺秀良，尹 霖，赵云飞

(陆军军事交通学院 基础部，天津 300161)

折射率是介质的一个重要物理参量，折射率的测量是普通物理光学实验的重要内容.普通物理实验室常用的测量透明固体折射率的仪器有分光计、迈克耳孙干涉仪、阿贝折射仪等.常用的测量方法可分为几何光学和波动光学.几何光学方法主要有：折射定律、最小偏向角法、全反射法等[1-4].在分光计上用最小偏向角法进行测量时，需要将被测材料制成棱镜且对棱镜的加工要求较高；全反射法的典型仪器为阿贝折射仪，测量中需要用到已知折射率的标准试件，且对被测材料折射率的大小有限制.波动光学方法主要有：干涉法[5-8]、Lau效应[9]、牛顿环法[10]等，其中干涉法最常见.在迈克耳孙干涉仪上利用白光干涉现象进行测量时，要求透明薄膜或者透明介质厚度很薄，否则操作不便；在分光计上利用多光束干涉测量时，条纹清晰度不易保证[11].

本文基于折射定律，利用移测显微镜对光线经过平行平板之后的微小偏移量进行测量，进而获取平行平板的折射率.该方法原理简单，是高中阶段常见实验 “插针法测玻璃折射率”的延续[12]，实验仪器可通过物理实验室普通常见光学仪器组装完成，实验过程涉及多种实验方法和实验技术，在教学中可作为物理实验自主实验项目，亦可作为折射率测量实验项目的拓展.

1 理论分析

假设透明平行平板介质位于绝对折射率为n0的介质中，厚度为d，绝对折射率为n1，如图1所示.光线以入射角i入射到透明平行平板介质，在前后2个面上发生折射.由于前后2个表面平行，该光线经过后表面折射后，出射光线相对于原入射光线产生横向偏移量L.

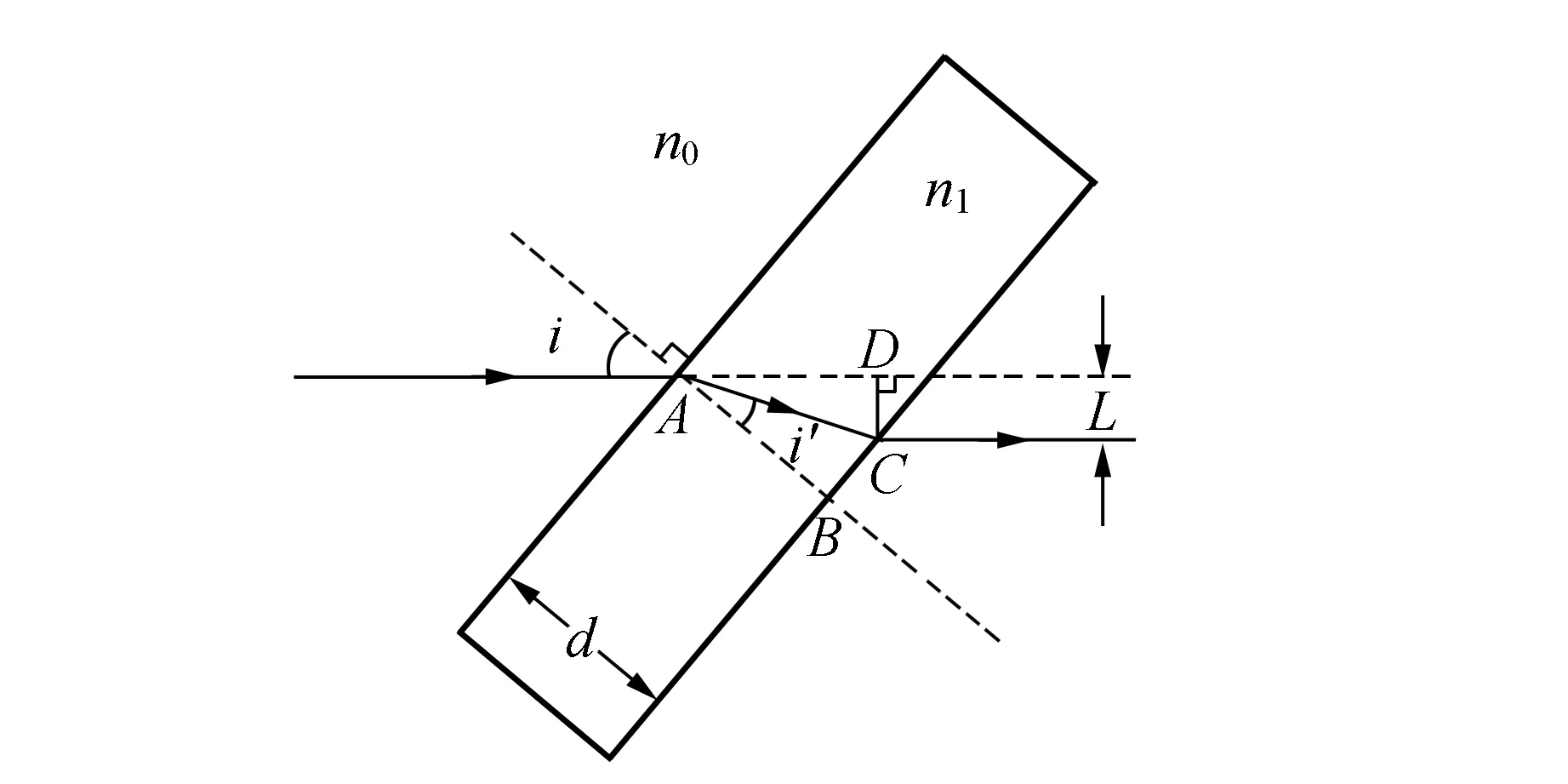
图1 测量原理图

利用求解△ACD的面积建立等式：

(1)

得到

(2)

将折射定律n0sini=n1sini′代入(2)式，得到

(3)

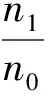
(4)

由式(4)可知，测出透明平行平板介质的厚度d、光线入射角i和折射光线的横向偏移量L，即可得到折射率n.

2 实验装置及操作方法

实验装置如图2所示，长焦距移测显微镜、测角盘、十字叉丝、毛玻璃屏和光源依次置于光具座上，其中测角盘的盘面水平并可绕竖直方向(z)旋转，长焦距移测显微镜和十字叉丝下方的底座可以沿x，y和z方向调节.

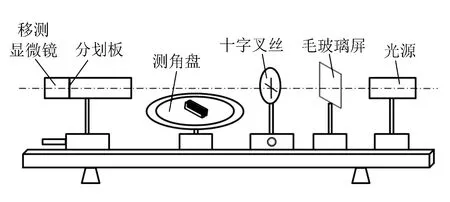
图2 实验装置图

测量时，利用被光源照亮的十字叉丝作为物，通过定位测角盘上平行平板前后十字叉丝在移测显微镜中的成像位置，来确定测量入射角i时的起始位置，当平行平板转动i时，十字叉丝在移测显微镜中的成像位置会产生L的微小位移量，再利用千分尺测量平行平板的厚度d，代入式(4)即可得到折射率n.

具体操作如下：

1)目测粗调移测显微镜、测角盘、十字叉丝、毛玻璃屏和光源共轴；

2)调节移测显微镜，看清显微镜分划板及十字叉丝像，如图3所示，注意消除视差；

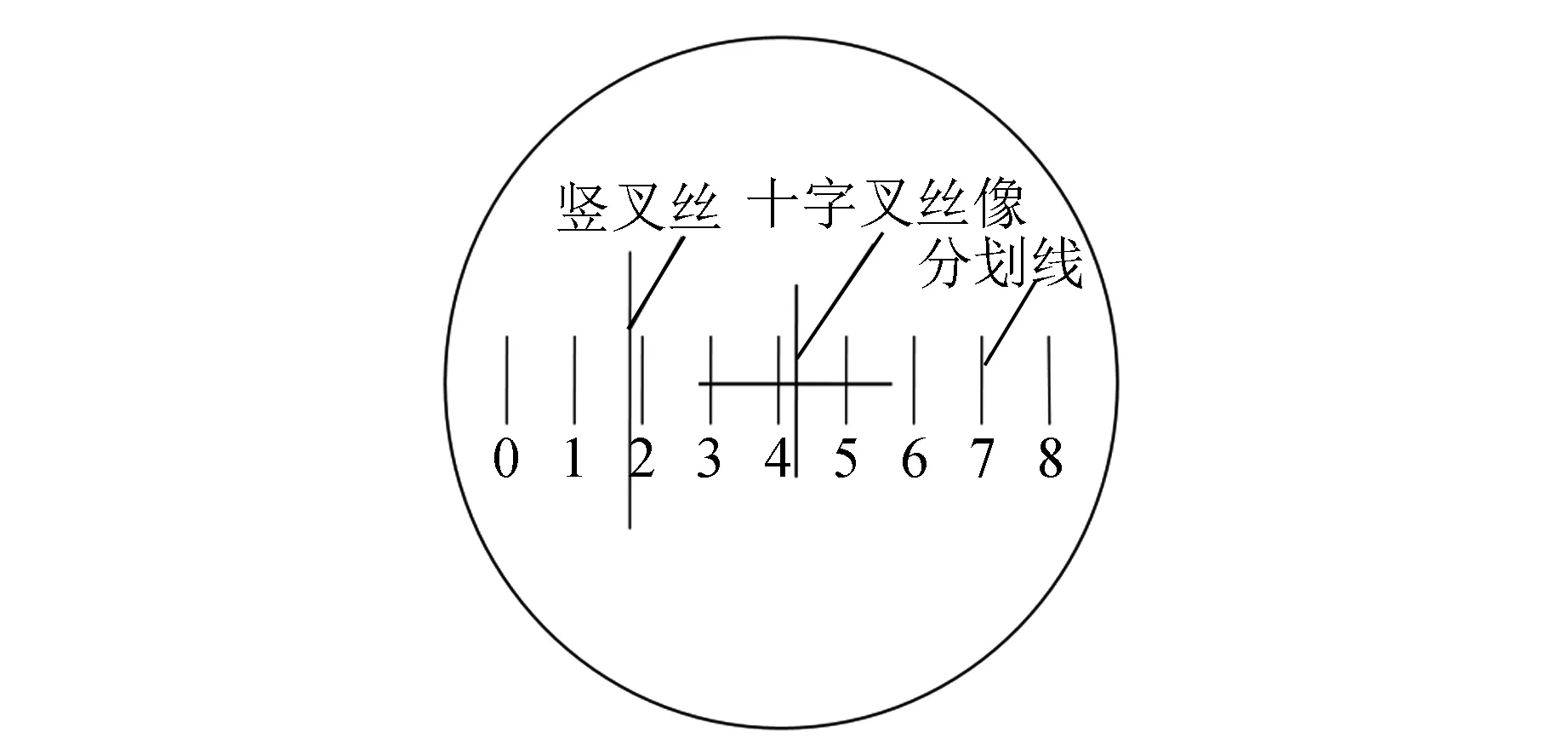
图3 显微镜内部分划板

3)调节十字叉丝下方三维调节架，使十字叉丝的竖线与分划板中心的分划线(图3中示值为“ 4”的分划线)对齐.

4)细调时，将待测平行平板固定在测角盘中心的固定夹上，并保持两平行面与测角盘垂直.由于待测介质的加入，改变了十字叉丝到移测显微镜物镜的光程，因此会造成分划板上十字叉丝像变模糊，这时可调节移测显微镜的纵向测微头，使移测显微镜沿光轴靠近十字叉丝，直至十字叉丝像清晰无视差.

5)转动测角盘带动平行平板介质在水平面内转动.由于折射，分划板上十字叉丝像将做横向水平位移，转动测角盘，使十字叉丝仍处于原位置，此时可保证光线垂直入射到待测平行平板的平行面上，即测角盘所指示的角度值即为图1中入射角i=0 的位置.

6)转动移测显微镜鼓轮带动图3中竖叉丝移动，将竖叉丝与十字叉丝竖线、分划板中心分划线对齐，记下此时移测显微镜示数.

7)继续沿同方向转动测角盘(注意避免空程)，记录多组测角盘示值和与之对应的十字叉丝竖线的位置.根据记录的数据，可分别计算入射角i和横向偏移量L.

3 误差分析

3.1 不确定度计算公式及各参量数值分析

根据式(4)，由不确定度传递公式

其中φ=F(x,y,z…)，x,y,z…是直接测量结果,可以推导出待测介质折射率n的标准不确定的表达式为[13]

(5)

由(5)式可知，折射率的标准不确定度与i,L,d具有复杂的函数关系.以下先从理论上分别分析i,L,d对不确定度的贡献，并给出计算机模拟的结果.

关于入射角i的不确定度的计算，实验用测角盘最大允差为2′.由于各入射角均是通过i=θ-θ0计算得到，因此，ui的计算仍需进行误差传递.假设测角盘仪器误差满足均匀分布，则ui=4.75×10-4rad.

关于偏移量L的不确定度的计算，实验用移测显微镜最大允差为0.005 mm.同入射角i的不确定度计算相同，uL=4.08×10-3mm.

关于平行平板的厚度d的不确定度的计算，因是经多次重复测量得到，d的不确定度包含A类分量和B类分量，已知所用螺旋测微器最大允差为0.004 mm，这里做保守估计，令ud=1×10-2mm.

3.2 入射角i及厚度d对折射率的不确定度的影响

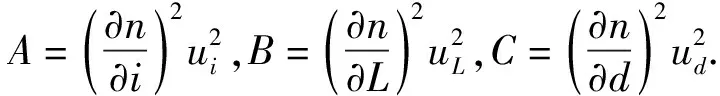
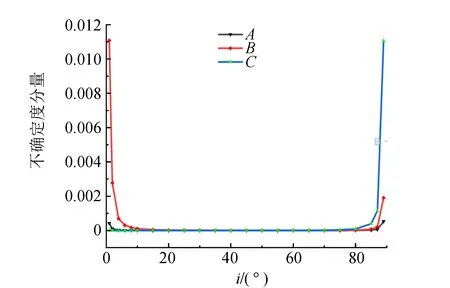
图4 不同入射角下各参量对不确定度的贡献对比(d=5 mm,n=1.5)

图5计算了n=1.5时折射率n的标准不确定度un与入射角i和平行平板厚度d的关系.从图5中可以看到，当厚度d一定时，un随着入射角的增大是先减小后增大，在40°附近达到极小值；当入射角i一定时，un随着d的增加而逐渐减小，数据分析表明，d<3 mm时un迅速减小，在d>3 mm以后减小的趋势逐渐放缓，并且在d>10 mm以后已很不明显.实验中，对un的要求不同将会影响到实验中入射角和平行平板厚度的范围选择.若希望得到较高的测量精度，则要选择相对厚的平行平板.计算结果表明，un的极小值约为0.001，此时如果想进一步减小un，提高n的测量精度，则需要从改进仪器设备着手.

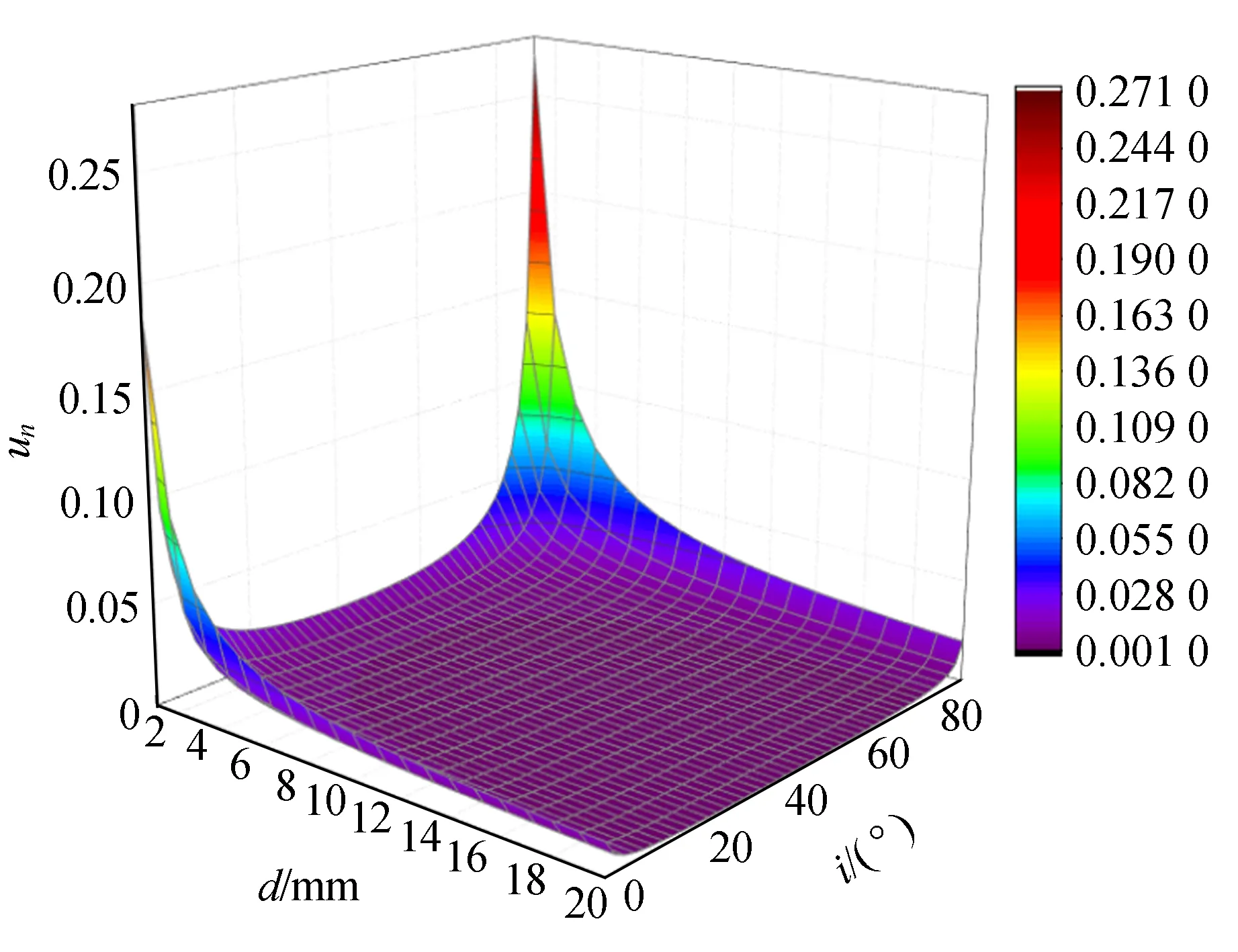
图5 不同入射角时折射率的标准不确定度(n=1.5)

3.3 显微镜系统景深对平行平板厚度的限制

显微镜系统景深包含显微镜自身景深[14]和眼睛调节景深.由图1可推导出介质厚度与景深应满足：

(6)

其中l为显微镜自身和眼睛调节景深之和，其余参量与前面定义相同.由于景深的限制，由(6)式可知，当景深相同时，入射角i越大，对应的介质厚度就越小.对于较厚的平行平板，可以通过降低对测角范围的要求而达到同样精度的测量结果.例如，取l=1.5 mm(不同人眼调节能力不同，此值有差别)，n=1.5，imax=70°进行估算，计算可得d=3.5 mm，但若现有平行平板厚度d=10 mm，则入射角的测量范围可取20°～40°.

3.4 实验设计要求

综合分析，在满足以上给定条件及大学物理实验教学要求的前提下，可按照相对偏差在1%以内对平行平板的厚度和入射角的范围作出规定，可选择厚度d在3～10 mm之间、入射角i在20°～70°展开测量，对应un的范围为2×10-3～7×10-3.由于人眼调节能力的不同，入射角i=70°只是满足精度要求的入射角的上限，实际入射角的上限应以测量过程中无视差为准.同时，通过计算还可以得出平板的折射率n越大，un越大，精度越低，如图6所示.因此，物理实验中还可以选择低折射率的平行平板来开展实验.

图6 不同折射率时的标准不确定度

4 实验结果分析

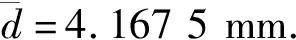
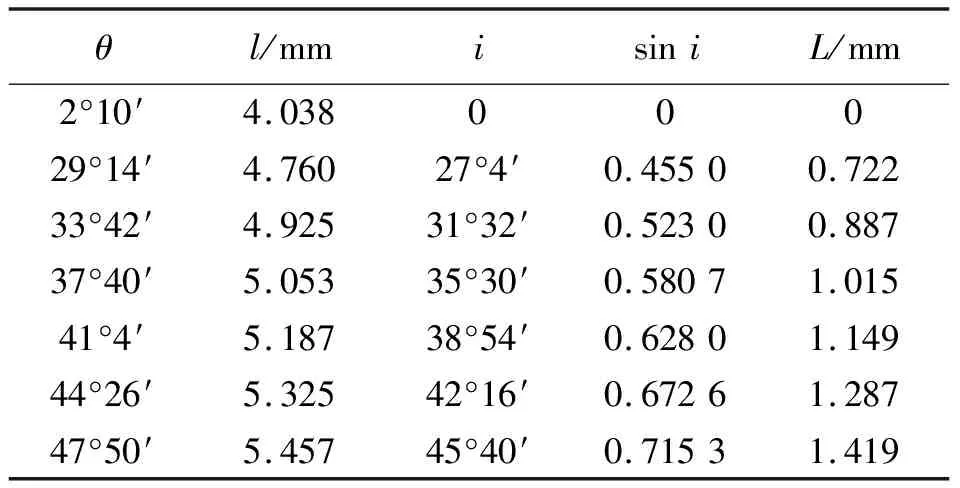
表1 测量数据表

由式(3)可知：

可以在Origin软件中利用自定义公式进行非线性曲线拟合求解折射率n[16].拟合时将厚度d设定为常量代入公式，进行单参数拟合.设自变量x=sini，因变量y=L，则拟合公式可变为：

y=d*x*(1-(1-x∧2)∧0.5/(n∧2-x∧2)∧0.5)，

拟合结果如图7.折射率n的最终结果为

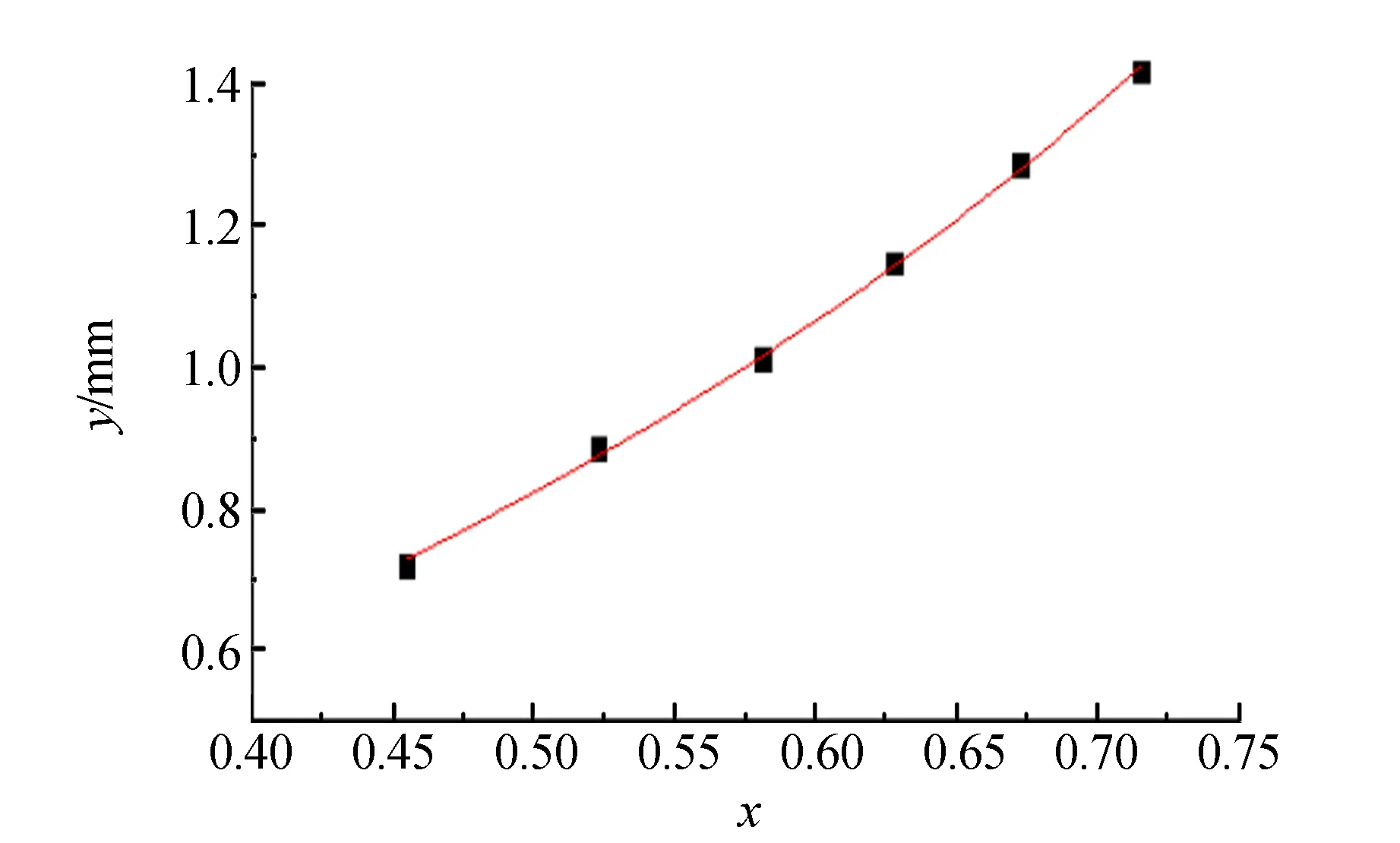
图7 拟合结果图

n=1.520±0.006(P=0.95).

该结果与用阿贝折射仪的测量结果n=1.518 9一致.数据点与拟合曲线几乎完全吻合，实验方法的可靠性和入射角的测量范围及待测介质厚度选择范围的合理性.

5 结束语

依据折射定律，利用移测显微镜对光线通过平行平板的微小偏移量进行测量，获得平行平板的折射率.通过误差分析，给出了光线入射角度、平行平板厚度和可测折射率的合理范围.实验中利用实验室现有元器件组装测量仪器，对微小偏移量、入射角度、平行平板厚度的测量均采用放大法，实验操作涵盖光路的共轴调整、对准和调焦调节、避免空程调节，数据处理利用软件Origin.本实验设计原理简单，操作难易适中，满足大学物理实验的教学要求，是对现有折射率测量相关实验项目的拓展，有利于培养学生的动手能力和创新能力.