使用mossbSim软件模拟穆斯堡尔实验

王思广，罗棱尹，贾春燕

(北京大学 物理学院 核物理与核技术国家重点实验室，北京 100871)

穆斯堡尔谱仪分辨能力高，可精确探测原子核能级的变化，在物质结构研究领域有许多应用实例[1-7].北京大学开设穆斯堡尔实验[8]课程多年.穆斯堡尔实验涉及到的物理知识与常规的近代物理实验所研究的射线与物质的相互作用有本质区别，其实验设计非常巧妙，教学过程有些问题值得思考，例如：为什么选用薄的探测器用于穆斯堡尔实验？将振动幅度增加1倍后穆斯堡尔谱会如何变化？如果上、下阈卡得不合适会如何影响最后的穆斯堡尔谱？放射源与样品之间的距离对穆斯堡尔谱有何影响？由于实验条件限制，实验室未配备不同厚度的探测器进行实验验证，实验课堂教学时间也不允许学生调节不同振动速度的幅度多次实验进行检验.理论讲解对于初步接触γ射线与探测器的学生非常抽象.为了让学生深入了解实验，利用Geant4软件包[9-10]开发了穆斯堡尔实验的模拟软件mossbSim.

1 穆斯堡尔实验原理

1957年，穆斯堡尔研究191Ir的γ射线的共振散射现象时发现了穆斯堡尔效应：在固体中的核发射或吸收γ射线时存在部分原子核无反冲的现象.要理解原子核无反冲对于穆斯堡尔实验的重要性，需要比对能级宽度与反冲能量的量级.

如果1个核的激发态寿命为τ，则其在退激发出的γ射线的能量不单一.能量分布I(E)与发出的γ射线的能量E之间的关系通常用洛伦兹函数描述：

(1)

(2)

对于静止的原子核，通过能级差为E0的跃迁发出动量为pγ、能量为Eγ的γ射线后，原子核的反冲能量为

(3)

式中c是光在真空中的速度.

我校穆斯堡尔实验用57Co放射源.根据以上公式及57Fe的第一激发态与基态之间的14.4 keV的能级差，可以计算出发生跃迁时的反冲能量为ER≈2×10-3eV.由于该能级的寿命τ≈0.1 μs，可以计算出对应的自然宽度Γ=4.9×10-9eV.因为所发出的γ射线的能量的改变ER远大于共振的自然宽度Γ，故如果出现原子核反冲，就不可能观察到14.4 keV的γ射线打在处于基态的57Fe原子组成的样品上被共振吸收跃迁到第一激发态的现象.

发生共振吸收后，由于第一激发态的能级寿命τ仅约0.1 μs，故激发后的原子核将很快退激，再次放出14.4 keV的γ射线.与被吸收的γ射线相比，新放出的γ射线的出射方向各向同性，故有很大概率要偏离被吸收的射线的方向.如果放射源、样品、探测器在1条轴线上，且样品在放射源及探测器之间，这种吸收再发射的过程将导致探测器测量到的计数减少.

为了显示出发生共振时探测器探测到的计数率与不发生共振时的计数率的不同，在穆斯堡尔实验中，放射源相对样品的运动速度将被逐渐改变，将探测器探测到的14.4 keV的射线峰的计数按照不同的补偿运动速度段进行顺序存储.反复测量不同的补偿速度对应的探测器探测到的14.4 keV能峰的计数(在能峰两侧设置上、下阈，记录该峰内的计数).最后得到穆斯堡尔谱.如果补偿速度扫描范围包含各共振位置而且超出的范围不算过大，就会看到清晰的补偿速度满足共振条件与不满足共振条件时的计数率的差异：发生共振吸收时，在穆斯堡尔谱上对应位置出现吸收谷.

上述通过相对速度的改变而增减γ射线的能量的原理系多普勒效应.能量改变ED与放射源发出的γ射线的能量Eγ及相对于样品的速度v成正比：

(4)

其中，θ是放射源运动方向与发出的γ射线的出射方向之间的夹角.

对于57Fe的14.4 keV的γ射线，如果放射源的运动速度为1 mm/s，通过多普勒效应对其改变的能量ED约为4.80×10-8eV，约为该能级10倍的自然宽度，α-Fe的穆斯堡尔谱各共振点所需要的补偿速度的扫描范围大致在±6 mm/s内.

基于以上理论，用Geant4软件包开发了模拟穆斯堡尔实验的软件mossbSim.

2 模拟的核心方法

根据57Co衰变到57Fe的衰变纲图[8]中提供的射线能量及分支比，利用能量分布函数I(E)抽样出57Fe退激放出的γ射线的能量Eγ，抽样定出γ射线的飞行方向，给出γ射线的四动量.然后根据衰变时刻的补偿速度v计算出补偿能量ED，得到调制后的γ射线新的四动量.

跟踪模拟能量补偿后的射线与物质的相互作用的任务由Geant4常规功能完成.但是样品吸收γ射线再发射的过程需要用到Geant4的G4VFastSimulationModel特殊处理模块.在mossbSim软件中的做法是：在样品的中间加了1层与样品材质相同的α-Fe膜，膜的厚度比样品的厚度至少小2个量级.当Geant4跟踪模拟γ射线到这层膜时，利用自行设计的程序根据γ射线的截面σ(E)函数进行抽样，决定发生共振吸收还是沿着原来的射线方向穿过这层膜.如果抽样结果是穿过这层膜，将γ射线沿其动量方向移到膜的外边界与样品材质的交界处(在样品内部)的点，并从交界点处沿着原来的方向且保持原来的动量继续模拟与物质的相互作用.如果抽样的结果是发生共振吸收，则通过随机抽样的方法确定共振吸收后退激放出新的γ射线的方向，该方向与原来的入射方向无关(模拟原子核退激各向同性随机放出γ射线的物理现象)，新的γ射线的能量与被吸收的γ射线的能量、位置相同.将新的γ射线从其产生位置，沿其动量方向移到膜的外边界与样品材料的交界处(在样品内部)，然后继续模拟其与物质的相互作用，直到打在探测器(这里用的是NaI晶体)上将部分或全部能量沉积下来或者跟踪到感兴趣区域外.被吸收的γ射线在吸收发生时直接被杀死.

借助模拟时逐渐增大的Geant4事件序号(Event ID)，实现速度扫描：用当前的事件序号与总道数(这里用512道)计算得到余数i，定出该事件模拟得到的信号放在第i道.然后根据预设的速度变化规律，计算出第i道对应的扫描速度v，根据v计算出补偿能量.最后抽样给出这个事件产生的射线数量及对应的能量和角度，计算出考虑补偿能量后的各射线的实际能量，模拟计算出该事件在探测器有效灵敏体积内沉积的能量总和及产生的总的光学光子数n，进而判断n是否介于预设的上、下阈之间，如果是则在第i道加1.

设置各共振位对应的补偿能量基于α-Fe的6条谱线v1，v2，…，v6的已知条件：

1)v6-v1=10.656 mm/s；

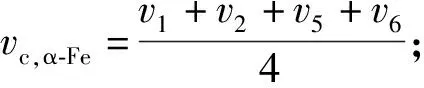
3)各谱线之间的能级间距已知[8].

3 模拟结果

首先模拟57Co放射源的能谱.如图1所示，X为道数，N为每道计数.红色竖线为所设置的14.4 keV的γ射线产生的信号峰左、右两侧的阈值.No.1能峰对应能量为6.4 keV的Fe的X射线，No.2能峰对应14.4 keV的γ射线，No.3能峰为123 keV及137 keV的γ射线在NaI中I元素产生的X射线逃逸后的剩余能量产生的信号峰，No.4为123 keV及137 keV的γ射线全能峰共同组成的信号.

图1 模拟NaI探测器探测到的57Co放射源的 衰变能谱图

模拟所用的NaI探测器晶体厚度为0.1 mm，模拟过程中考虑了57Fe的第二激发态到基态的跃迁发出的137 keV的γ射线，第二激发态到第一激发态的跃迁发出的123 keV的γ射线，第一激发态到基态的跃迁发出的14.4 keV的γ射线及第一激发态通过内转换过程使得内层电子电离引发的Fe的K系标识X射线(模拟用的X射线能量是6.4 keV).

依据图1所示的能谱，可以对14.4 keV的峰设置上、下阈，观察落在上、下阈之间的信号所对应的补偿速度的分布，即穆斯堡尔谱，如图2所示.探测器厚度为0.1 mm，补偿振动速度范围为±8 mm/s.与实验获取的穆斯堡尔谱表示方法一致.其中X轴与补偿速度v之间有转换关系，该转换关系是模拟程序预设的(mossbSim中预设了第1道对应于+v，中间第256道对应于-v，第512道对应于+v，其中+v到-v再到+v的过程系匀减速及匀加速变化).因在第1道至第512道之间对应的补偿速度经历了先减小再增大的过程，故如果设置的速度变化范围±v内包括了这6个共振位置，则每个模拟周期会经历2次共振点，故所模拟出的α-Fe的穆斯堡尔谱有12个共振位置，并且关于速度变化的转折位置(这里是第256道)左右对称.

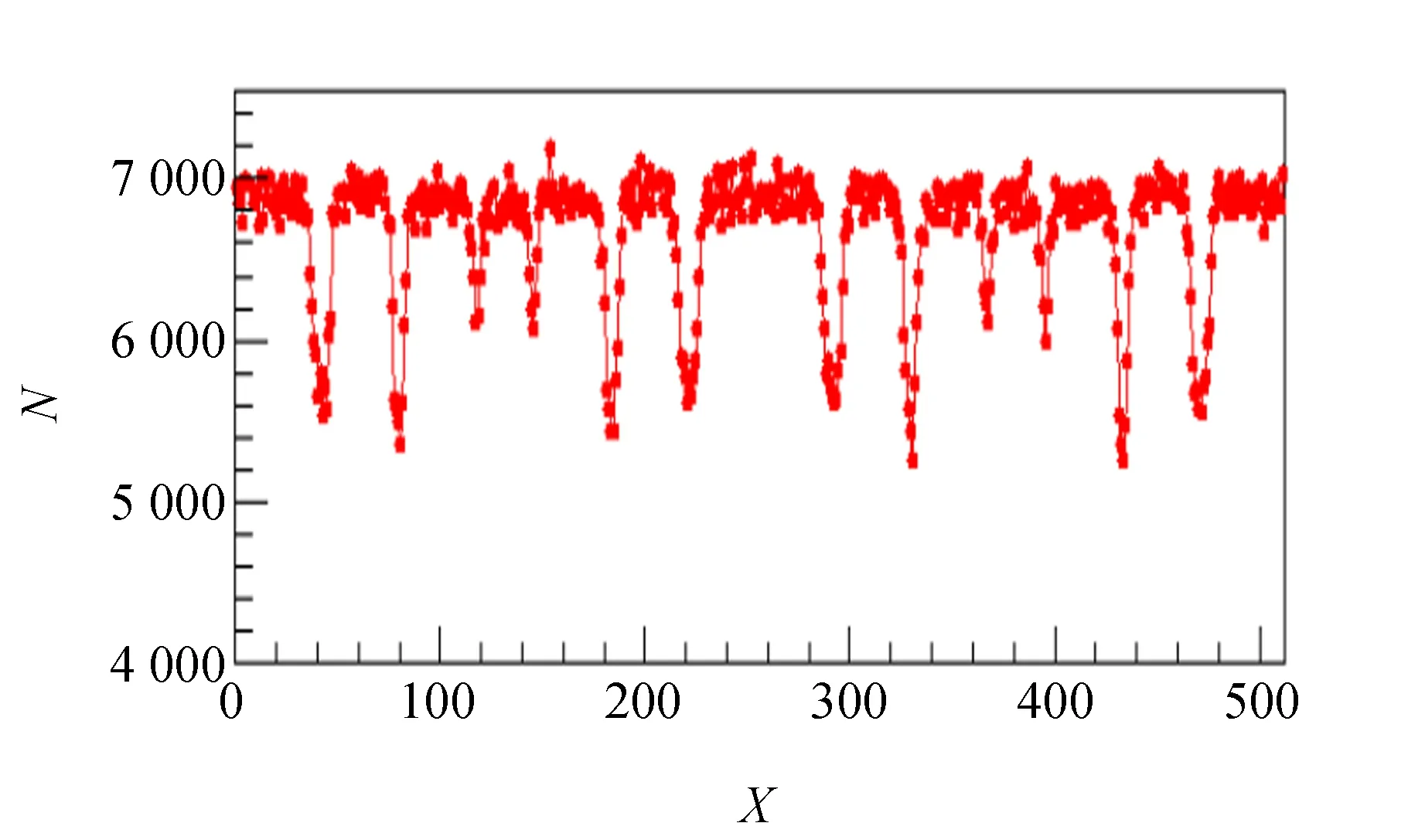
图2 将补偿振动速度范围设置为±8 mm/s后 模拟α-Fe的穆斯堡尔谱

考虑到补偿能量与补偿速度的一一对应关系，如果将振动速度的范围增加或减小，则共振位置将因所对应的补偿速度位于坐标轴上的相对位置变化而变化.为了验证这点，将振动速度范围由原来的±8 mm/s提高到±20 mm/s后，所得到的穆斯堡尔谱如图3所示.

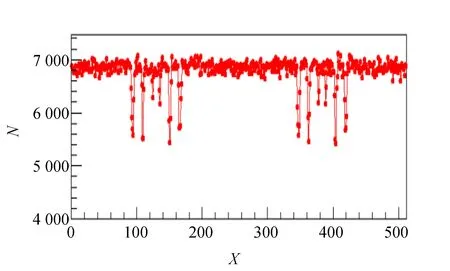
图3 将补偿振动速度范围设置为±20 mm/s后模拟的α-Fe的穆斯堡尔谱

图2和图3的明显差异在于图3较图2中共振点之间的距离收缩(以道数表示)，但实际上如果以补偿速度描述共振点的距离，图2与图3上相邻的共振点所对应的补偿速度应该完全相同，当然共振点间的补偿速度之差也应该完全相同.

以上模拟所用的探测器的厚度为0.1 mm.选用如此薄的探测器的原因主要是为了压低放射源发射的123 keV及137 keV的γ射线对实验结果产生的干扰：实验选用的放射源为57Co，其发出的γ射线中除用来观察穆斯堡尔现象的14.4 keV的γ射线，还有123 keV和137 keV的γ射线，并且两射线的分支比分别为91%及9%，因从第一激发态退激到基态发出14.4 keV的γ射线有内转换过程与其进行竞争，内转换系数α=15(即发出内转换电子的概率与发出γ射线的概率之比为15∶1)，故14.4 keV的γ射线的实际分支比非常小，约为5.7%，具体参阅参考文献[8]提供的衰变纲图.123 keV的γ射线与14.4 keV的γ射线有级联衰变效应，即从第二激发态跃迁到第一激发态发出123 keV的γ射线后，因第一激发态的能级寿命很短，故很快继续跃迁到基态发射出14.4 keV的γ射线或通过内转换过程发射出内转换电子.如果这2条前后时间相差很小的γ射线几乎同时发出并都被探测器探测到，而探测器的响应时间较慢，无法区分2条γ射线，则探测器给出的总的能量将为2条γ射线在探测器上沉积的能量相加，这种真符合效应将减少14.4 keV信号数.对于14.4 keV的γ射线，很薄的1层NaI晶体就能够将其能量完全沉积下.而对于能量比其高的123 keV的γ射线，因穿透能力较强，故被探测到的效率低，通过真符合效应对14.4 keV的信号影响小.

同样的原因，对于薄的探测器，137 keV的γ射线通过偶然符合对14.4 keV的信号的影响也小.但是，如果选用厚的探测器，因为对123 keV以及137 keV的γ射线的效率的提高而导致对14.4 keV的γ射线的符合效应的影响增大.

另外，如果选用厚的探测器，123 keV以及137 keV的γ射线在14.4 keV能峰附近产生的康普顿散射平台将比较薄的探测器上产生的康普顿散射平台高，从而感兴趣的14.4 keV信号的信噪比低.

为了验证以上说法，将NaI的厚度分别设为0.1，0.5，10.0mm进行模拟，得到57Co的能谱如图4所示，对应的穆斯堡尔谱如图5所示.从图4可以看出:随着探测器厚度的增加，123 keV以及137 keV组成的复合峰包的γ射线信号的幅度较14.4 keV的γ射线峰的幅度迅速增加.从图5也可以看出：随着探测器厚度的增加，模拟同样的事件数(每种厚度条件下模拟的事件总数均为1×1010)得到的最后谱图中的总计数也增加.

图4 模拟NaI探测器晶体的厚度分别为0.1，0.5，10.0 mm时57Co放射源的衰变能谱图

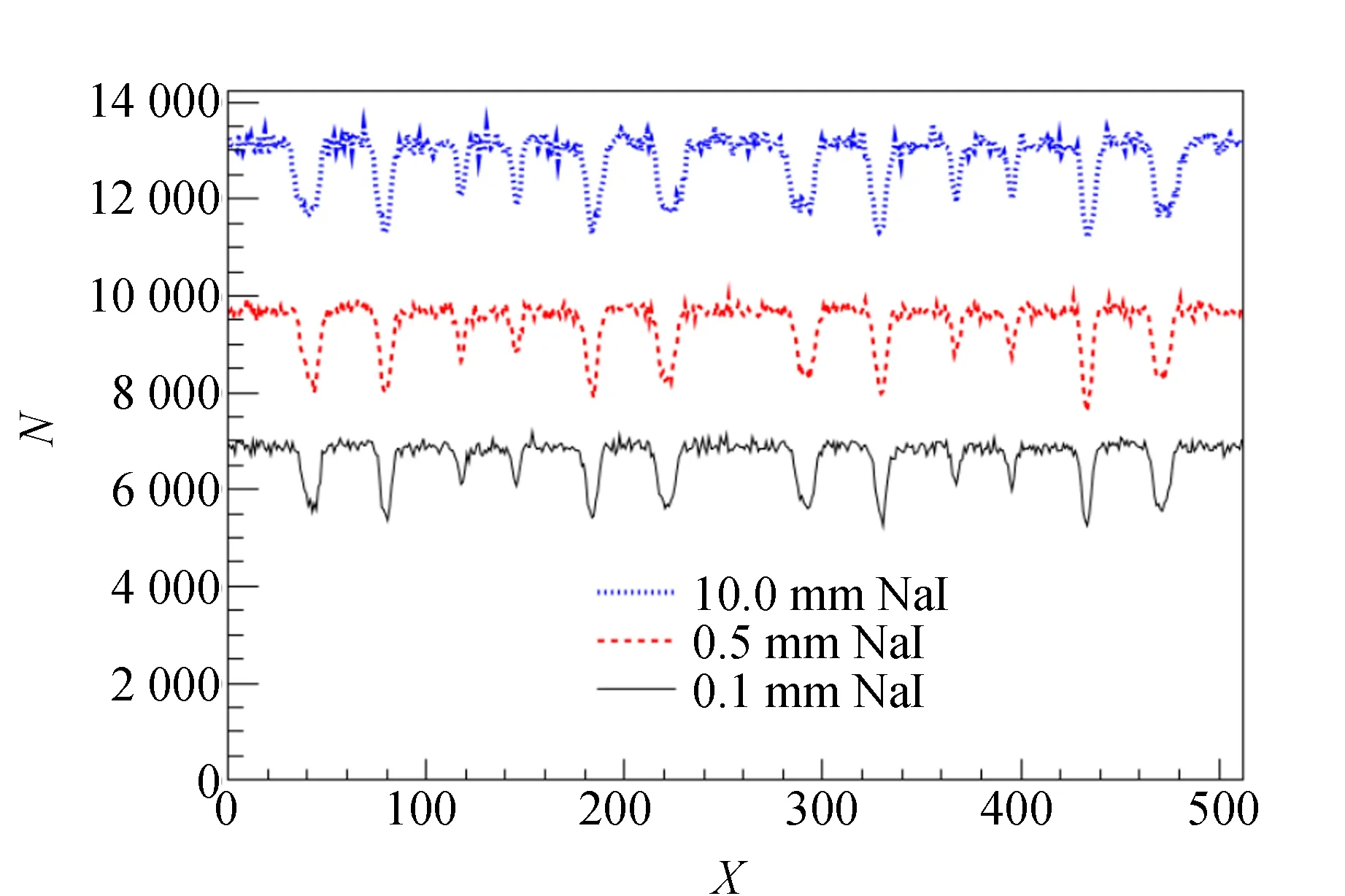
图5 模拟NaI探测器晶体的厚度分别为0.1，0.5，10.0 mm时所测得的穆斯堡尔谱

为了便于比较图5中共振点对应的谷的深度与本底基线的比例(对于穆斯堡尔谱，本文定义该比值为信噪比)，将各穆斯堡尔谱进行归一化，如图6所示.

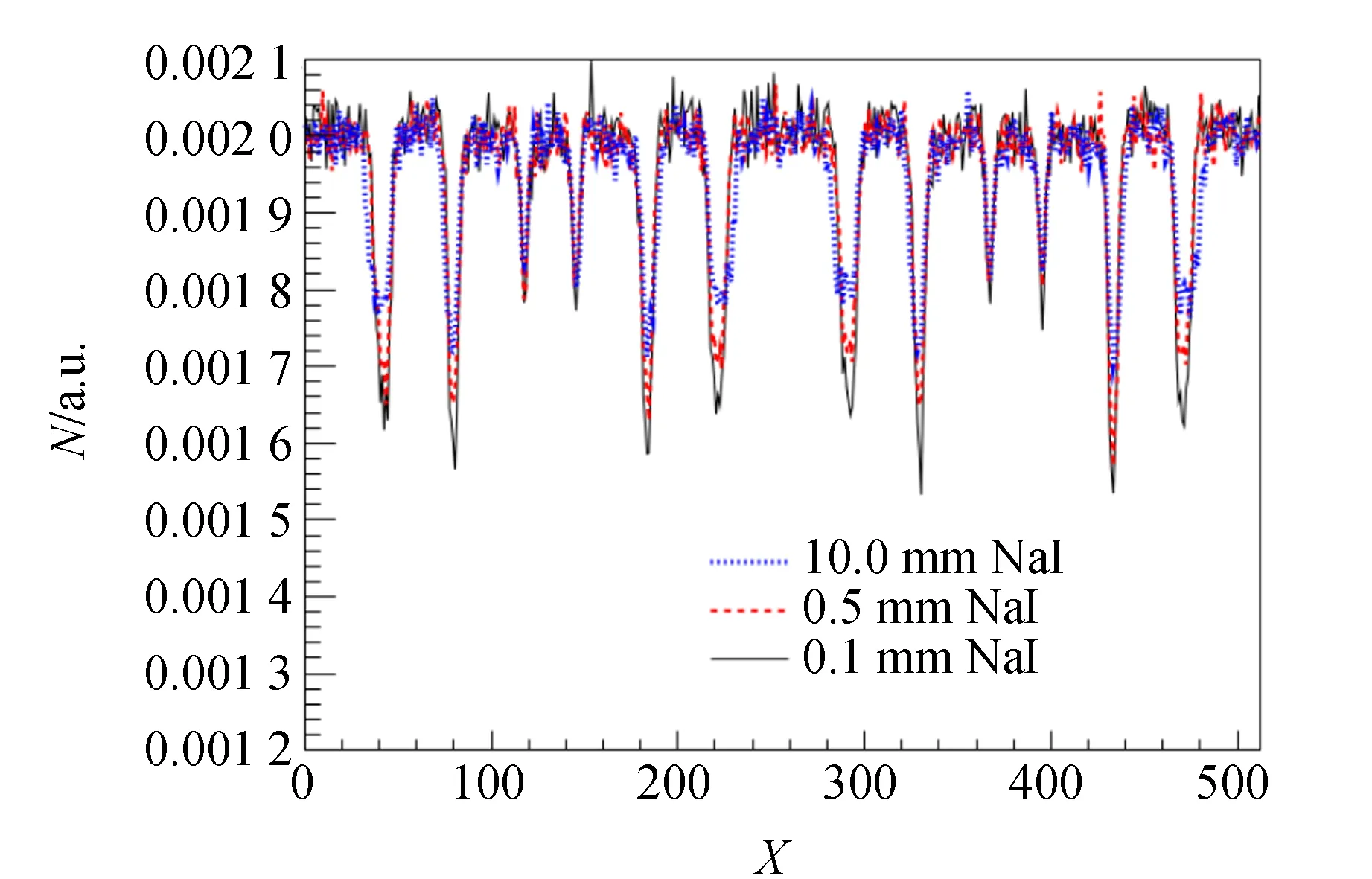
图6 模拟NaI探测器晶体的厚度分别为0.1，0.5，10.0 mm时的归一化穆斯堡尔谱

从图6可以看出：0.1 mm厚度的探测器所探测到穆斯堡尔谱上的共振信号的信噪比好于10.0 mm厚的探测器得到的信噪比.另外，因电子学处理每个信号都需要一定的时间，故实验中123 keV及137 keV的γ射线在厚的探测器中因探测效率的增加将增加谱仪的死时间率.故选用较薄的探测器.

图2～6都基于图1所示的上、下阈区间挑选的信号给出的穆斯堡尔谱.如果该上、下阈区间选取不合适，例如误将6.4 keV的X射线峰及其下本底包含在阈值内，因这些射线不会发生共振吸收，故它们抬高了整个基线的高度而对共振信号谷的深度的增大没有实质贡献，最终将导致信噪比拉低.

图7给出对于同样厚度的探测器设置不同上、下阈后的差异.图7中标记为“Wrong range”谱数据系将图1所示的上、下阈区间范围由原来的35～65道扩展为5～65道，扩展后的上、下阈包含6.4 keV的峰及峰下本底计数.标记为“Right range”谱数据与图2中的穆斯堡尔谱数据相同.2种谱数据各自归一化后画在一起.显然标记为“Wrong range”的穆斯堡尔谱信号的信噪比要比标记为“Right range”的穆斯堡尔谱信号的信噪比差.

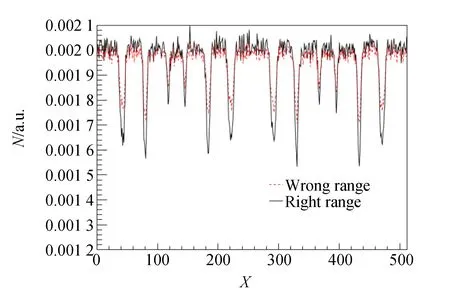
图7 设置不同上、下阈所得的穆斯堡尔谱图

利用mossbSim模拟软件，也可以研究放射源与样品之间距离对穆斯堡尔谱的影响.图8所示系放射源距离样品5 mm及100 mm所对应的穆斯堡尔谱.显然距离较近时的穆斯堡尔谱分辨变差.可以引导学生从距离短时大角度入射到样品中的射线份额比例较大进行思考原因.

图8中12个谷对应着共振点的位置.左侧1～6号吸收谷在模拟程序中被设置的初始相对强度分别为1.0，0.8，0.3，0.3，0.8，1.0,其中1号与6号所需要的补偿速度较2号和5号大.D=5 mm时，因当入射角较小与较大的射线不能同时满足共振条件，故1号和6号对应的分辨率较后者差，吸收谷变宽，导致深度反而不如2号和5号谷.D=100 mm时入射角差异不大，故分辨率较好.

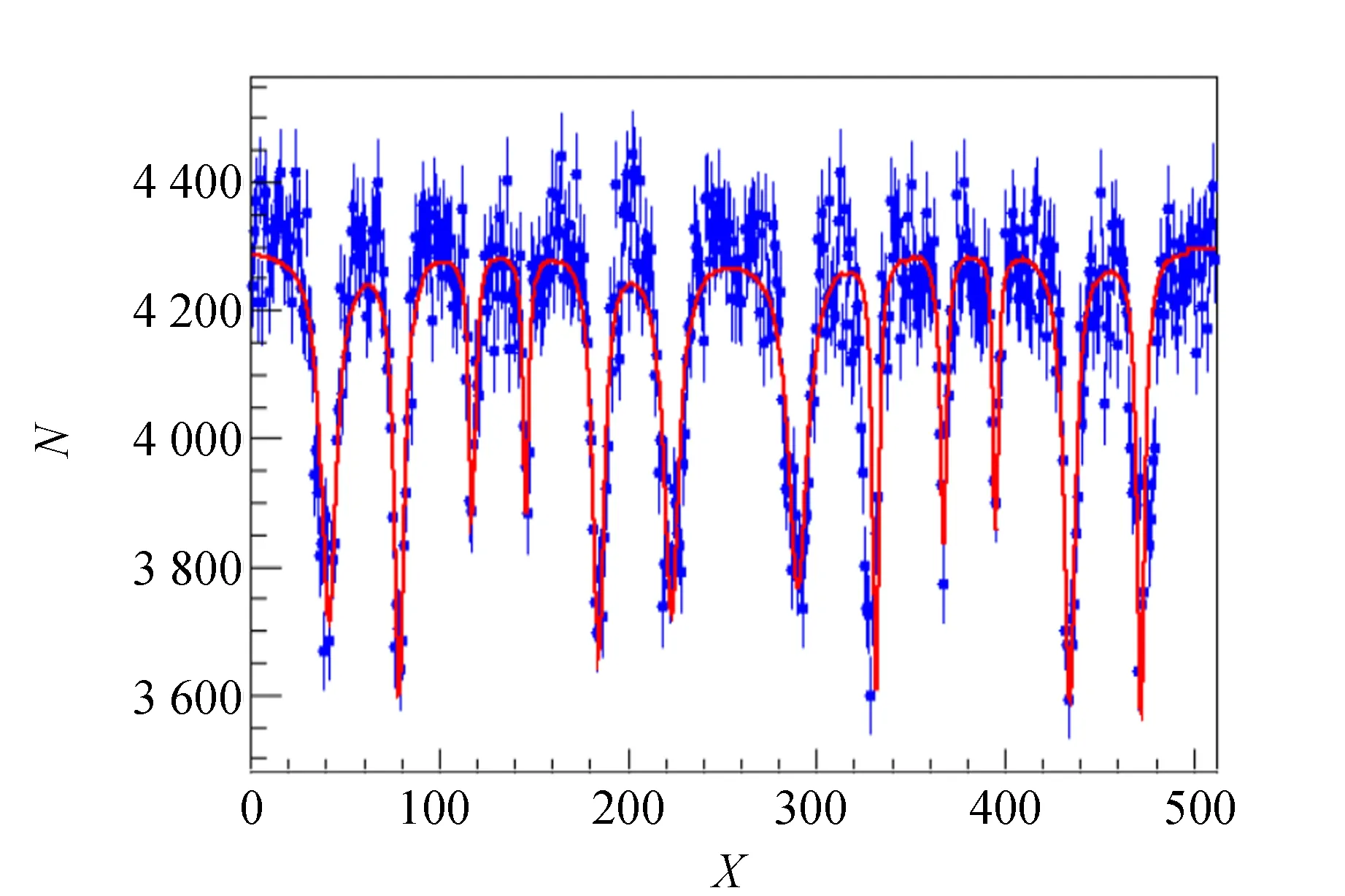
(a)D=5 mm

除以上列举的改变相关参量进行穆斯堡尔谱形状的研究外，学生也可以从源代码上做多样化的探究，比如：为研究振动系统不完美的状况下对穆斯堡尔谱的影响，可将振动速度由现有的匀加速和匀减速改变换成曲线变化的速度增减；加入振动的空程差(加减速度时有偏移量，即道址与振动速度不是一一对应，而是人为随机加入错位)，观察有、无空程差的穆斯堡尔谱之间的差异；改变探测器的分辨率，即将沉积的能量与转换成的光子数对应的系数改变，研究探测器的分辨率与共振信号的宽度、信噪比之间的关系.

mossbSim软件模拟结果存储为ROOT文件形式[11]，其优点是可以很方便地进行数据分析并画图比较.也为学生提供了可以将ROOT数据格式文件转换为普通文本格式文件的程序，供不愿学习ROOT软件的学生利用分析实验数据的方法分析模拟数据，以便将实验数据的分析结果与理论模拟数据的分析结果进行比较.

作为比较，图9为实验穆斯堡尔谱图.模拟的穆斯堡尔谱(图8)与实验谱相似.细微差异主要来自于探测器各组成的尺寸参量及扫描速度的差异.模拟中各吸收谷的相对强度是临时设置的1组数据，与实际也有差异.如果将实验装置的各参量输入准确，可以通过比较模拟与实际测得的穆斯堡尔谱给出α-Fe共振谷的相对强度.模拟的输出、输入比值可作为数据处理过程所需的探测效率修正因子.故本模拟软件可以作为细致研究穆斯堡尔谱的起点.

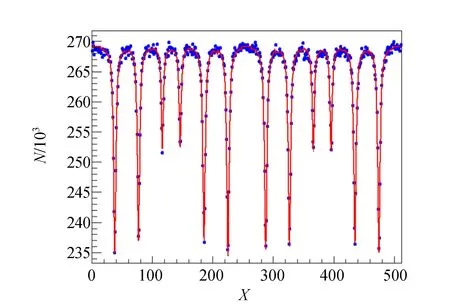
图9 α-Fe样品的实验穆斯堡尔谱图

4 结束语

利用Geant4开发了模拟穆斯堡尔实验的软件mossbSim.该软件的核心是利用Geant4的G4VFastSimulationModel功能模块处理样品共振吸收再发射的过程，实现了穆斯堡尔实验的蒙特卡罗模拟.利用mossbSim软件，学生可以调节探测器的厚度、速度振动范围，对14.4 keV的峰设置不同的上、下阈，模拟出α-Fe的穆斯堡尔谱.通过模拟，学生将会深入理解穆斯堡尔效应的原理；通过对模拟代码的研究，将有助于了解和掌握Geant4这一通用的开源模拟软件包的基本功能，同时该软件也为学生提供接触ROOT分析软件的机会.将该软件应用于教学课堂的优点是学生可以学到很多模拟及数据分析相关的知识，缺点是对任课教师要求比较高(需要Linux相关的基本知识).为了减轻教师负担，我们也准备了教学录像，学生可以通过多媒体演示了解程序的运行方式.全部源代码见http://wlsy.nenu.edu.cn/doku.php?id=wenzhang:2101:wsg.