高中数学“一题多解”教学的反思

姜 娜

(山东省日照黄海高级中学 276800)

一、教学中妙用一题多解

高中数学教学不仅应重视基本知识技能的传授，还应强调培养学生分析和解决问题的能力，培养学生的数学思维，提高学生的数学素养.为实现这一教学目标，需要运用有效的教学方式和方法.一题多解就是一种高效的数学思维训练方法，针对同一问题，通过多角度审视和分析，有助于拓展学生的思维，激发学生的创新性思维，培养学生的发散性思维，使学生能够灵活运用所学知识解决实际问题，将所学知识巩固、深化和拓展.一题多解是当前高中数学教学不可或缺的重要方法之一.下面结合具体实例加以说明和分析.

例1等差数列{an}中，a1<0,S9=S12,请问数列{an}前几项的和最小？

所以，当n=10或n=11时，Sn的值最小.即数列前10项或前11项的和最小.

点评本解法是按常规思路分析，根据等差数列的概念公式来解答.通过运用数学公式促进学生熟练掌握数学公式.要知道，熟练记忆数学公式是学好数学的关键.

解法2因为S9=S12，所以a10+a11+a12=3a11=0.解得a11=0.

又因为a1<0,所以公差d>0,由此可得数列{an}前10项或前11项和最小.

点评此解法是通过找转折项来破解此题.运用了等差中项的性质，使解题思路更巧妙，解题过程更简捷，同时也锻炼了学生对数列知识的灵活运用能力，杜绝了对数学公式和性质的死记硬背，有助于拓展学生的思维拓展.

点评函数思想是高中数学解题中常见的数学思想方法之一，它可简明揭示一种变量间的联系，通过图象观察就可以解决其最值问题.将数列问题转化为函数问题，利用函数的性质、思想可迅速解决，实现数学知识和思想的迁移与运用.

点评在解关于等差数列最值问题时，其解题基本思想就是找出某一项，使该项及其前面的项都取正值或负值或0，而其后面的项则都取负值或正值，那么，第1项至该项的各项和即为最大或最小值.

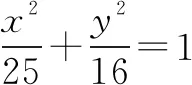
A.有两个点PB.有四个点P

C.可能不存在点PD.一定不存在点P

解法1将F1F2作为直径构圆，已知圆的半径r=c=3<4=b，所以圆与椭圆不相交，即不存在点P.

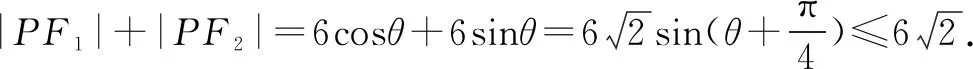
二、教学反思

“一题多解”教学可有效调动学生的思维积极性，拓宽学生的思维空间，丰富学生的数学认知，有助于发散性思维的培养，使学生面对事物，能够以更全面、多元、多视角地进行思考，并找出有效的解决方法，这对于培养学生的问题解决能力有重要意义.

1.有助于培养发散思维

面对同一题目，引导学生进行多角度分析，运用不同的数学思想和知识，找出多种解决策略，使学生认清问题的本质，体会数学思想的奥妙.在这样的学习过程中，学生的思维在不断地猜想、验证、拓展、碰撞，有助于激发学生的探究热情，活跃学生的思维，使学生处于思维亢奋状态，有效提高学生数学学习的效率，也提高了学生的解题能力.

2.有助于培养创新思维

学生教育最重要的是创新意识和精神的培养，这也是高中数学课程目标之一.“一题多解”就是要帮助学生在通往成功的道路上找出那条最简单、高效的方法和思路，能够迅速解决问题.我们知道“殊途同归”的含义，但不同的道路付出的代价是不同的.数学解题同样也需要以最小的代价(时间、脑力等)换取最有效的答案.这样的解题过程才具有挑战性，才具有创新性，才能真正锻炼学生的数学思维，考验学生的基本知识技能.这种创造性思维需要不断加以训练才能形成，“一题多解”的学习方式就像一把钥匙，能够将学生的思维潜能之锁一一打开，使学生的思维更加多样化、新颖化.

3.有助于教学思想的延伸

通过“一题多解”教学法的探讨，可将这种教学思维延伸至一题多问模式，这也有助于学生全面、多元化认知实际问题.比如，平时做选择题时，同学们只是选出正确答案就算完成了，对其它的备选答案并不关注，这对于考试答卷来说，无可厚非，但在教学中，这样的过程过于简单，不利于培养学生的思维多样性.应找出其它错误答案的错误点在哪儿，并分析为什么会出错，在这种错答反思中也可以锻炼学生的思维，巩固所学知识.所以，错误资源同样不能浪费，要珍惜.再如，当讲授典型题目时，教师不仅要引导学生正确分析、思考，找出正确的解题方法，还要在讲解时，将易错点渗透其中，指出其错误原因，说明为什么会出现这样的错误思维，同时要对题目的命题意图和关键信息等加以讲评，让学生真正明白题目要考查的重点和难点，有助于学生真正理解题意，掌握答题策略.这样，由一道题开始，逐渐扩展成全面的、多角度的考核，将单一的知识点联结在一起，形成一个知识体系，有助于学生更全面地掌握同类知识，明确答题技巧，使数学课堂教学更高效、高质.

总之，“一题多解”教学模式是一种有效的数学思维培养途径.通过对题目的全方位分析，寻求多种解题策略，是一种由知识到能力的演变，是学生思维质量的升华.通过一题多解的思维训练，不仅使学生更加牢固地掌握基础知识，加深对数学概念的理解和记忆，更重要的是使学生的思维更有深度和广度，能够自主发现题目背后隐藏的规律，举一反三，自主构建数学知识体系，使学生的解题能力得到有效提升，使学生的数学思维更加完善.从而顺利实现数学课程教学目标，培养出优秀的数学人才.