弹簧振子碰撞问题归类分析

胡连冬

(湖南省长沙宁乡市第七高级中学 410635)

弹簧振子的碰撞问题涉及相互作用观、运动观、动量和能量观，知识综合性强，物理现象复杂，运动过程多变；这类问题能很好的区分学生的综合素养，因而成为历年高考命题的重要素材之一.

一、弹簧振子的定义

如图1所示，把轻弹簧的一端固定，另一端连接小球或滑块，当轻弹簧发生形变后，小球或滑块就在平衡位置附近作往复运动，这种现象叫简谐振动，其中弹簧和小球或滑块组成的系统称为弹簧振子.如图2中在轻弹簧的两端各连接一个小球，当弹簧发生形变后，该系统中的两个小球就相对系统的质心作简谐振动，这样的系统称为“弹簧双振子模型”，弹簧振子是一种理想化模型.

二、弹簧振子的碰撞问题

1.竖直弹簧振子的碰撞问题

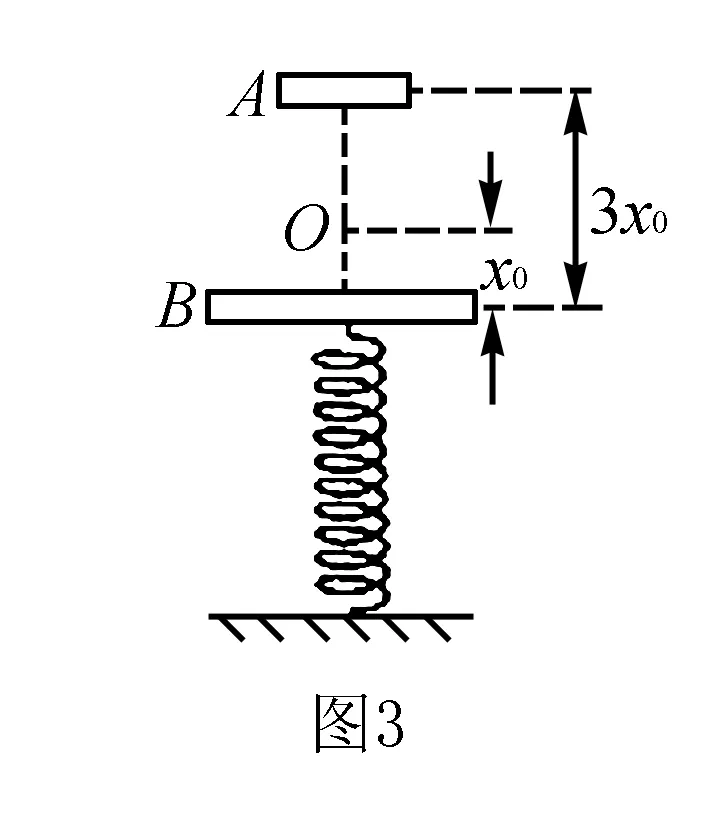
例1质量为m的钢板与直立轻弹簧的上端连接，弹簧下端固定在地上.平衡时弹簧的压缩量为x0，如图3所示.一物块从钢板正上方距离为3x0的A处自由落下，打在钢板上并立刻与钢板一起向下运动，但不粘连.它们到达最低点后又向上运动.已知物块质量为m时，它们恰能回到O点.若物块质量为2m，仍从A处自由落下，则物块与钢板回到O点时，还具有向上的速度.求物块向上运动到达的最高点与O点的距离.

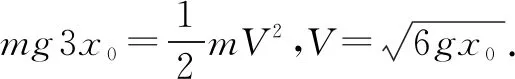
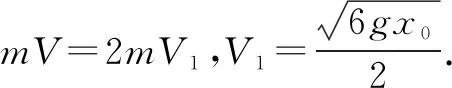
设弹簧压缩x0时的弹性势能为Ep.在物块与钢板碰撞后直到物块恰好回到O点的过程中，物块与钢板及弹簧组成的系统机械能守恒，即：

(1)

物块与钢板碰撞后瞬间的速度为V2.

物块与钢板回到O点时，还具有向上的速度V3.同理物块与钢板及弹簧组成的系统机械能守恒，则：

(2)

物块返回O点后作竖直上抛运动，物块向上运动到达的最高点与O点的距离为hm.此过程物块机械能守恒，

(3)

点评本题的解题关键是对物理过程做好仔细分析，甄别每个过程遵循的物理规律.本题的难点是对弹性势能的理解，弹簧的弹性势能不要求写出具体表达式，可用Ep表示，但要理解弹簧的弹性势能只与弹簧形变有关；同一弹簧形变相同，则弹性势能Ep相同；弹簧形变为零，则Ep为为零.

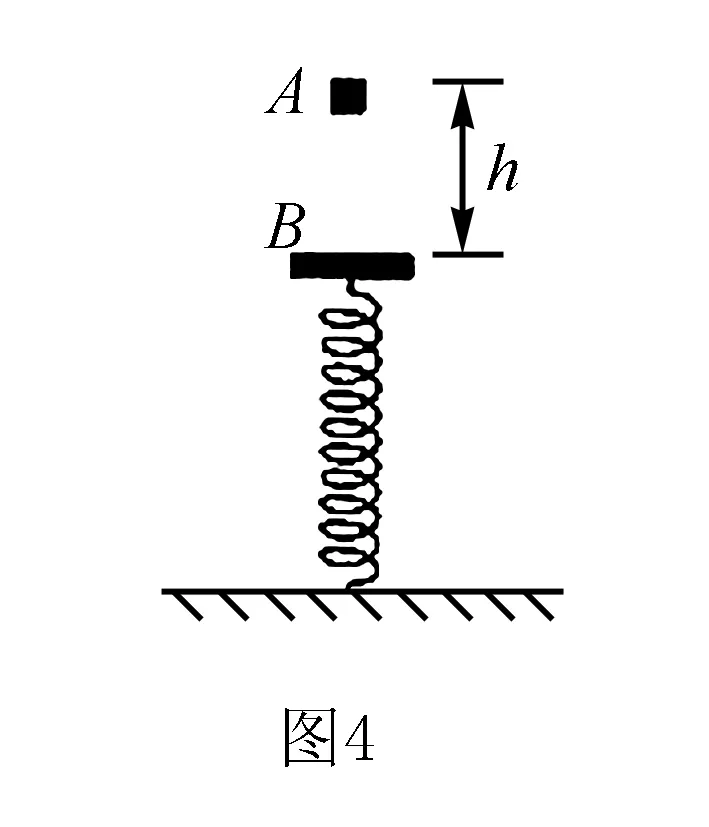
例2如图4所示，一个劲度系数为k的轻弹簧竖直立于水平地面上，下端固定于地面，上端与一质量为m的平板B相连而处于静止状态.今有另一质量为m的物块A从B的正上方h高处自由下落，与B发生碰撞而粘在一起，已知它们共同向下运动到速度最大时，系统增加的弹性势能与动能相等，求系统的这一最大速度v.

解析A下落到与B碰前的速度v1为：

①

A、B碰后的共同速度v2为：

mv1=(m+m)v2

②

B静止在弹簧上时，弹簧的压缩量为x0，且：

mg=kx0

③

A、B一起向下运动到最大速度v时的位移为x，此时A、B的加速度为0，即有：

2mg=k(x+x0)

④

由机械能守恒得：

⑤

⑥

点评本题的难点在于理解AB共同运动何时速度最大.当弹簧振子振动的过程中受到的弹簧的弹力是变力，其合力也是变力，振子从平衡位置向下运动时，振子所受合力减小，振子作加速度减小的加速运动，当合力为零，即加速度为零时，振子速度最大.因此有2mg=k(x+x0).由此可见，要正确处理弹簧振子的碰撞问题，振子的受力分析和运动情况分析是解题过程中必不可少的思维环节.

2.水平弹簧振子的碰撞问题

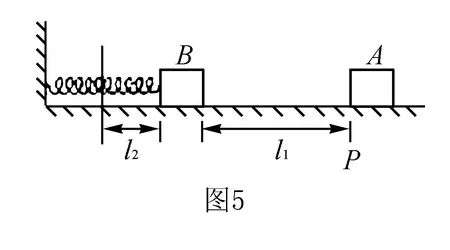
例3轻弹簧的一端固定，另一端与滑块B相连，B静止在水平直导轨上，弹簧处在原长状态.另一质量与B相同滑块A，从导轨上的P点以某一初速度向B滑行，如图5所示；当A滑过距离l1时，与B相碰，碰撞时间极短，碰后A、B紧贴在一起运动，但互不粘连.已知最后A恰好返回出发点P并停止，滑块A和B与导轨的滑动摩擦因数都为μ，运动过程中弹簧最大形变量为l2，重力加速度为g，求A从P出发时的初速度v0.

解析令A、B质量皆为m，A刚接触B时速度为v1(碰前)，由功能关系有

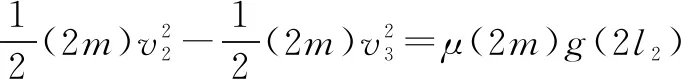
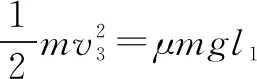
点评弹簧振子在碰撞瞬间，由于作用时间极短，弹簧来不及发生形变，因此振子碰撞瞬间AB系统动量守恒；对于AB滑块何时分离要有清晰的物理情景，振子A受弹簧弹力约束，在AB弹回的过程中，当弹簧恢复原长时，滑块AB间无相互作用，AB刚好分离，这是分析本题要厘清的临界点.其次AB碰撞前后系统中各个物体的运动过程是否符合机械能守恒条件，还是只能由能量守恒或动能定理来处理运动过程中的能量关系，对能量观念也要有清醒的认识.

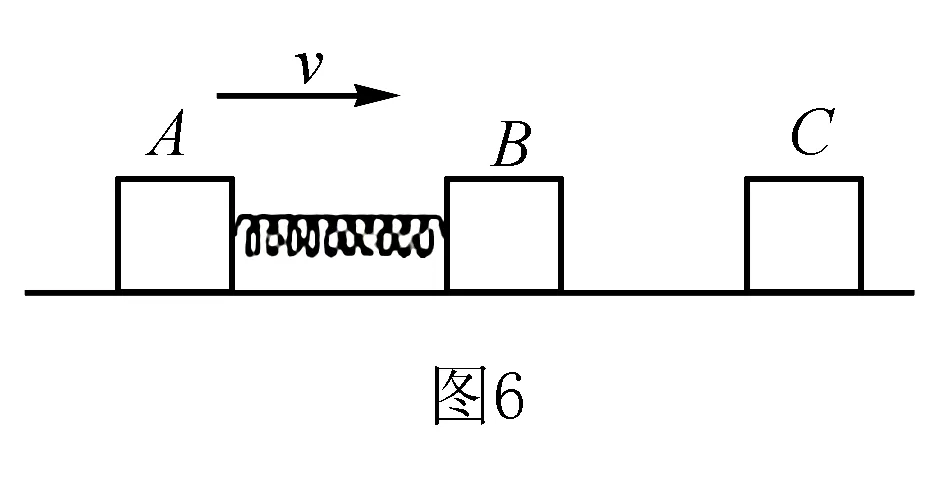
例4用轻弹簧相连的质量均为2kg的A、B两物块都以v=6m/s的速度在光滑的水平地面上运动，弹簧处于原长，质量为4kg的物体C静止在前方，如图6所示，B与C碰撞后二者粘在一起运动.求：在以后的运动中，

(1)当弹簧的弹性势能最大时物体A的速度多大？

(2)弹性势能的最大值是多大？

(3)A的速度有可能向左吗？为什么？

解析(1)当A、B、C三者的速度相等时弹簧的弹性势能最大，由于A、B、C三者组成的系统动量守恒，有

(mA+mB)v=(mA+mB+mC)vA

解得：vA=3m/s

(2)B、C碰撞时B、C组成的系统动量守恒，设碰后瞬间B、C两者速度为v′则mBv=(mB+mC)v′,v′=2m/s

设物块A速度为vA时弹簧的弹性势能最大为Ep，根据能量守恒

(3)由系统动量守恒得

mAv+mBv=mAvA+(mB+mC)vB

设A的速度方向向左，vA<0,则vB>4m/s

则作用后A、B、C系统总的机械能

点评针对弹簧双振子碰撞问题，要善于通过分析双振子的受力情况，准确把握双振子的运动情况；当双振子系统内各物体速度相等时，弹簧形变量最大，弹簧的弹性势能最大.同时分析此类问题要切合双振子运动的实际情况，碰撞前后系统的能量不增加，否则违背了能量守恒定律.

3.斜面上弹簧双振子碰撞问题

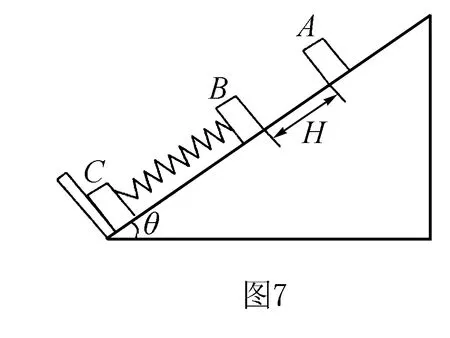
例5如图7所示，在一个倾角为θ的光滑斜面底端有一个挡板,物体B和物体C用劲度系数为k的轻弹簧连接,静止在斜面上.将一个物体A从距离物体B为H处由静止释放,沿斜面下落后与物体B碰撞,碰撞后A与B黏合在一起并立刻向下运动,在以后的运动中A、B不再分离.已知物体A、B、C的质量均为M,重力加速度为g,忽略各物体自身的大小及空气阻力.求：

(1)A与B碰撞后瞬间的速度大小.

(2)A和B一起运动达到最大速度时,物体C对挡板的压力为多大？

(3)开始时，物体A从距B多大距离由静止释放时,在以后的运动中才能使物体C恰好离开挡板？

解析(1)A与B碰撞前A的机械能守恒，即

①

AB碰撞瞬间系统动量守恒，若AB碰撞后共同速度为V.则

MVA=2MV

②

(2)AB碰撞后作加速度减小的加速运动，当AB的加速度为零时，AB运动速度最大，若此时弹簧弹力为F.则有：F=2Mgsinθ

因弹簧处于压缩状态，故物体C对挡板的压力为F′=F+Mgsinθ

即F′=3Mgsinθ

(3)AB碰撞后，弹簧振子沿斜面向下运动，直到弹簧压缩最短，要使物体C恰好离开挡板，即物体C与挡板无相互作用力，则此时弹簧弹力为：N=Mgsinθ

若弹簧伸长x有：Kx=Mgsinθ

③

在AB碰撞前和物块C刚好离开挡板这两个时刻，弹簧形变量相同，弹性势能EP也相同.设物体A距B为h处由静止释放，由于A碰撞前机械能守恒、AB碰撞时系统动量守恒、AB碰撞后系统机械能守恒得到：

④

MVA=2MV

⑤

⑥

点评斜面上弹簧双振子碰撞问题跟水平弹簧双振子碰撞问题分析方法相似，只是振子在斜面上运动有重力势能的变化，因此处理问题时要特别注意振子系统内物体受力情况和运动情况分析；审题时要注意题目中关键的“字”、“词”、“句”读懂其意义，充分挖掘隐含条件；如本题中第(3)小问“使物体C‘恰好’离开挡板”，即弹簧伸长刚好最大时，C与挡板之间无作用，此时振子AB发生的位移最大且速度刚好为零.

4.弹簧双振子碰撞中的图像问题

例6如图8甲所示，质量分别为m=1 kg、M=2 kg的A、B两个小物块用轻弹簧相连而静止在光滑水平面上,在A的左侧某处另有一个质量也为m=1 kg的小物块C以VC=4 m/s的速度向右正对A匀速运动,一旦与A接触后就将黏合在一起运动.若在C与A接触前对A施加一个水平向右的瞬时冲量I,从A获得瞬时冲量作用的时刻开始计时,取向右为正方向,其速度随时间变化的图象如图乙所示(C与A未接触前),弹簧始终未超出弹性限度.求：

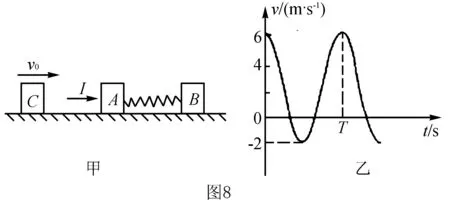
(1)对A施加的瞬时冲量I的大小；

(2)在C与A接触前,当A的速度分别为6 m/s、2 m/s、-2 m/s时,求对应状态下B的速度,并在此基础上粗略画出B的速度随时间变化的图象；

(3)若C分别在A的速度为vA1=4 m/s 、vA2=-2 m/s时与A接触,试分析这两种情况下在接触后的运动过程中弹性势能最大值Epm1和Epm2.

解析(1)观察图乙，A的水平初速为V0=6 m/s.

由动量定理得：I=mV0. 对A施加的瞬时冲量的大小为6Ns.

(2) 当A获得水平初速6 m/s后，AB和弹簧组成的系统水平方向动量守恒，即：mV0=mVA+MVB.故当A的速度分别为6 m/s、2 m/s、-2 m/s时, 对应状态下B的速度分别为：0、2 m/s、4 m/s.

当AB第一次速度相同时，弹簧压缩到最短状态，此时弹簧弹性势能最大，若此时AB速度为V.由系统水平方向动量守恒有：

mV0=(M+m)V

①

以后B继续加速，而A作减速运动，直到弹簧恢复原长时B的速度最大，A的速度达到反向最大，此时弹簧弹性势能为零，AB速度分别为VAmVBm.根据系统的动量和能量守恒得：mV0=mVAm+MVBm

②

③

由以上三式解得：V=2 m/s,VAm=-2 m/s,VBm=4 m/s.

当弹簧恢复原长后，由于AB速度反向，A先减速后正向加速，B一直减速直到AB第二次速度相同，弹簧拉伸最长，此时AB速度为V=2 m/s.然后A继续加速运动速度达到正向最大6 m/s .而B继续减速直到速度减小到零,这时弹簧第二次恢复原长,此后AB两滑块速度重复以上周期性变化.因此AB两滑块速度图象关于V=2 m/s对称，如图9所示.

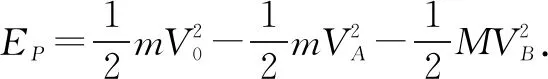
mVC+mVA=2mVCA

④

当CA和B速度相同时，弹簧的弹性势能最大，若CA和B的共同速度为V′.由系统动量守恒得：

2mVCA+MVB=(2m+M)V′

⑤

此时弹簧最大的弹性势能为：

⑥

由④⑤⑥得：EPm1=13.5 J

当VA=-2m/s时，B的速度为VB=4 m/s .此时弹簧处于原长，弹簧的弹性势能为零，若C与A碰撞，同理可得此后弹簧的最大弹性势能为EPm2=4.5 J.为何两种情况下弹簧的最大弹性势能不同呢？其原因是当VA=4 m/s时，C与A碰撞无能量损失，而当VA=-2m/s时，C与A碰撞能量损失最大.即C以VC=4 m/s的速度与A碰撞时CA和B及弹簧组成的系统在运动过程中弹簧弹性势能的变化范围为：4.5J≤EP≤13.5J.

点评弹簧双振子碰撞中的速度图象问题，涉及振子的受力分析和运动状态分析，由于双振子受弹簧弹力作变加速运动，振子的运动情况比较复杂，分析此类问题要善于把握两个临界状态：一是弹簧弹性势能最大时，双振子具有相同的速度，二是弹簧恢复原长时两振子的速度(或反向速度)必有一个达到最大.在求解弹簧的弹性势能时，要综合运用系统动量守恒和系统能量守恒两大规律，结合系统初末状态下的能量关系列方程求解.