指对同构法处理导数题

胡贵平

(甘肃省白银市第一中学 730900)

把一个等式或不等式通过变形,使左右两边结构形式完全相同，可构造函数，利用函数的单调性进行处理，找这个函数模型的方法就是同构法.对于复杂的导数题，无疑是一把利器.

一、指对同构模型

aea≤blnb有三种同构方式.

(1)可以保留左边，对右边同构，aea≤blnb即aea≤lnb·elnb，可构造函数F(x)=xex模型；

(2)可以保留右边，对左边同构，aea≤blnb即ea·lnea≤blnb,可构造函数F(x)=xlnx模型；

(3)可以两边取对数，对两边同构，aea≤blnb即a+lna≤lnb+ln(lnb),可构造函数F(x)=x+lnx模型.

1.blnb与xex同构

blnb=elnb·lnb，即lnb·elnb对应xex模型，可构造函数F(x)=xex.

例1 设实数λ>0,若对任意的x∈(0,+), 不等式恒成立，则λ的最小值为( ).

2.aea与xlnx同构

aea=lnea·ea，即ealnea对应xlnx模型，可构造函数F(x)=xlnx.

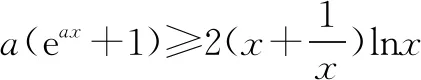
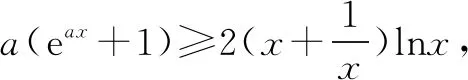
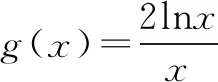
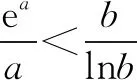
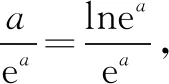
ea±a>b±lnb有两种同构方式.

(1)可以保留左边，对右边同构，ea±a>b±lnb即ea±a>elnb±lnb，可构造函数F(x)=ex±x模型；

(2)可以保留右边，对左边同构，ea±a>b±lnb即ea±lnea>b±lnb，可构造函数F(x)=x±lnx模型.

4.c+lnc与x+ex同构

c+lnc=elnc+lnc，即lnc+elnc对应x+ex模型，可构造函数F(x)=x+ex.

例4已知函数f(x)=ex+2ax(x∈R).

(1)求f(x)的单调性；

(2)已知a>0,令g(x)=f(x)-a(x-1)ln(ax-a)+a,若g(x)恒单调递增,求a的取值范围.

解析(1)f′(x)=ex+2a，当a≥0时，f(x)的增区间为(-,+)．

当a<0时，f(x)的减区间为(-,ln(-2a)),增区间为(ln(-2a),+)．

(2)g(x)=ex+2ax-a(x-1)ln(ax-a)+a定义域为(1,+),因为g(x)恒单调递增,所以g′(x)=ex-aln(ax-a)+a≥0在(1,+)恒成立．即所以ex-lna-lna≥ln(x-1)-1,所以ex-lna+(x-lna)≥eln(x-1)+ln(x-1)．令F(x)=ex+x,显然F(x)在(1,+)单调递增,所以原不等式等价于F(x-lna)≥F(ln(x-1)),所以x-lna≥ln(x-1),所以lna≤x-ln(x-1).令h(x)=x-ln(x-1)(x>1),则所以h(x)在(1,2)单调递减, 在(2,+)单调递增,所以h(x)min=h(2)=2，因此lna≤2，即a≤e2，所以a的取值范围是(0，e2].

二、高考中的应用

例5(2020年新全国Ⅰ山东)已知函数f(x)=aex-1-lnx+lna．

(1)当a=e时，求曲线y=f(x)在点(1，f(1))处的切线与两坐标轴围成的三角形的面积；

(2)若f(x)≥1，求a的取值范围．

在(0,1)上h′(x)>0,h(x)单调递增；在(1,+)上h′(x)<0,h(x)单调递减，所以h(x)max=h(1)=0,lna≥0，即a≥1，所以a的取值范围是[1,+).

例6(2018年全国新课标Ⅰ文)已知函数f(x)=aex-lnx-1．

(1)设x=2是f(x)的极值点，求a，并求f(x)的单调区间；

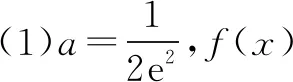
因为x>0，所以只需证xex≥exlnex.

即证xex≥elnexlnex构造函数F(x)=xex，只需证F(x)≥F(lnex).而F′(x)=(x+1)ex>0，于是F(x)在(0,+)上是增函数，所以只需证x≥lnex，即证x≥lnx+1．

令g(x)=x-lnx-1(0,+)，当x∈(0,1)时，g′(x)<0，从而g(x)在(0,1)上单调递减；当x∈(1,+)时，g′(x)>0，从而g(x)在(1,+)上单调递增．所以g(x)≥g(1)=0，即x≥lnx+1．所以当时，f(x)≥0．