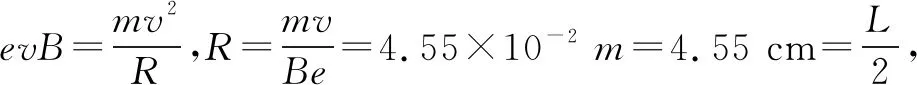从几道高考题谈有界磁场的临界与极值问题的数理方法

胡卫雄

(湖北省武汉市常青第一中学 430000)

在研究带电粒子在洛伦兹力作用下的圆周运动时，经常会遇到粒子通过有界磁场区域的运动情形，往往因为初始速度不同，所处的磁场磁感强度大小不定，运动圆轨迹在变化，同时由于边界的约束从而产生 “恰好”“最大”“至少”等临界与极值问题，本文以几道高考题为例，分类讨论通过带电粒子在有界磁场运动的的临界极值问题的数理分析方法.

一、带电粒子恰好不穿出磁场区域的临界问题

当带电粒子通过有界磁场区域时，如果带电粒子的初始速度不同，所处的磁场磁感强度大小不定，运动圆轨迹在变化，由于边界的约束从而产生“恰好”不穿出磁场区域的临界情形，此类问题一般需要推理出带电粒子恰好不穿出磁场区域的临界条件(在磁场中运动的轨迹与边界相切)，画出临界条件下的的运动轨迹图，应用“临界轨迹+几何关系”，结合带电粒子在洛伦兹力作用下的圆周运动的物理规律列方程联立求解．

例1 (2020·全国卷Ⅲ第18题)真空中有一匀强磁场，磁场边界为两个半径分别为a和3a的同轴圆柱面，磁场的方向与圆柱轴线平行，其横截面如图1所示.一速率为v的电子从圆心沿半径方向进入磁场.已知电子质量为m，电荷量为e，忽略重力.为使该电子的运动被限制在图中实线圆围成的区域内，磁场的磁感应强度最小为( ).

答案：C

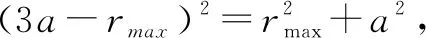
点评本题中，电子的速度大小恒定为v,方向确定为沿半径方向，因为磁感强度大小不确定，运动半径不确定.以入射点B为定点，圆心位于与初速度垂直的同一直线BA上，将半径放缩作轨迹，作出一组如图3所示的半径逐渐增大的“缩放圆”.分析中，重点在于利用放缩的动态轨迹圆，找出临界条件下(与半径为3a的圆柱面相切)的“临界轨迹”，分析临界条件下的几何关系，结合带电粒子在磁场中圆周运动的动力学规律求解.

二、带电粒子在有界磁场中运动时间的极值问题

当带电粒子通过有界磁场区域时，如果带电粒子的初始速度不同，运动圆半径不同，运动圆轨迹在变化，由于边界的约束，各粒子在磁场中运动的时间长短不一样，从而产生粒子在有界磁场中运动时间的极值求解问题.如果磁场的磁感强度恒定，带电粒子的荷质比相同，各粒子在磁场中运动的周期相同，则可根据圆心角判断时间的极值：粒子运动转过的圆心角越大，时间越长．此类问题一般需要推理出带电粒子在有界磁场中运动时间的极值条件(圆心角最大)，画出极值条件下的的运动轨迹图， 应用“极值轨迹+几何关系”，结合物理规律求解.如果不容易画出极值条件下的运动轨迹图，则可应用“一般轨迹+几何关系”，得到相关物理量之间的函数关系，通过数学方法求极值条件，再结合物理规律求解.

例2 (2020·全国卷Ⅰ第18题)一匀强磁场的磁感应强度大小为B，方向垂直于纸面向外，其边界如图4中虚线所示，ab为半圆，ac、bd与直径ab共线，ac间的距离等于半圆的半径.一束质量为m、电荷量为q(q>0)的粒子，在纸面内从c点垂直于ac射入磁场，这些粒子具有各种速率.不计粒子之间的相互作用.在磁场中运动时间最长的粒子，其运动时间为( ).

答案：C

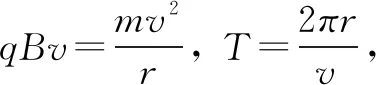
方法二：采用“一般轨迹+几何关系”，利用数学函数关系求极值解决该问题.假设粒子运动轨迹如图6所示,圆心在O点，ab半圆的圆心在O′，OO′=2R-r,Oe=r,O′e=R,由余弦定理有

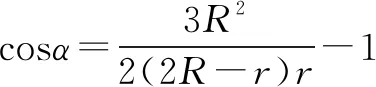
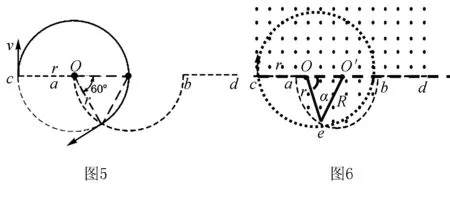
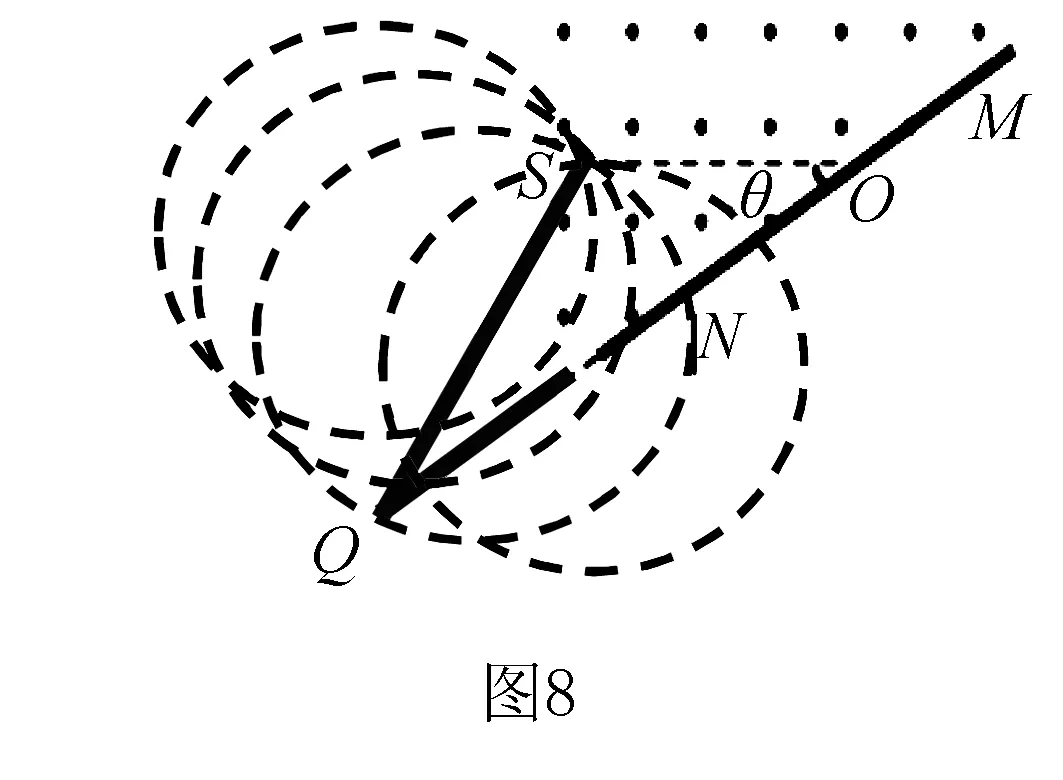
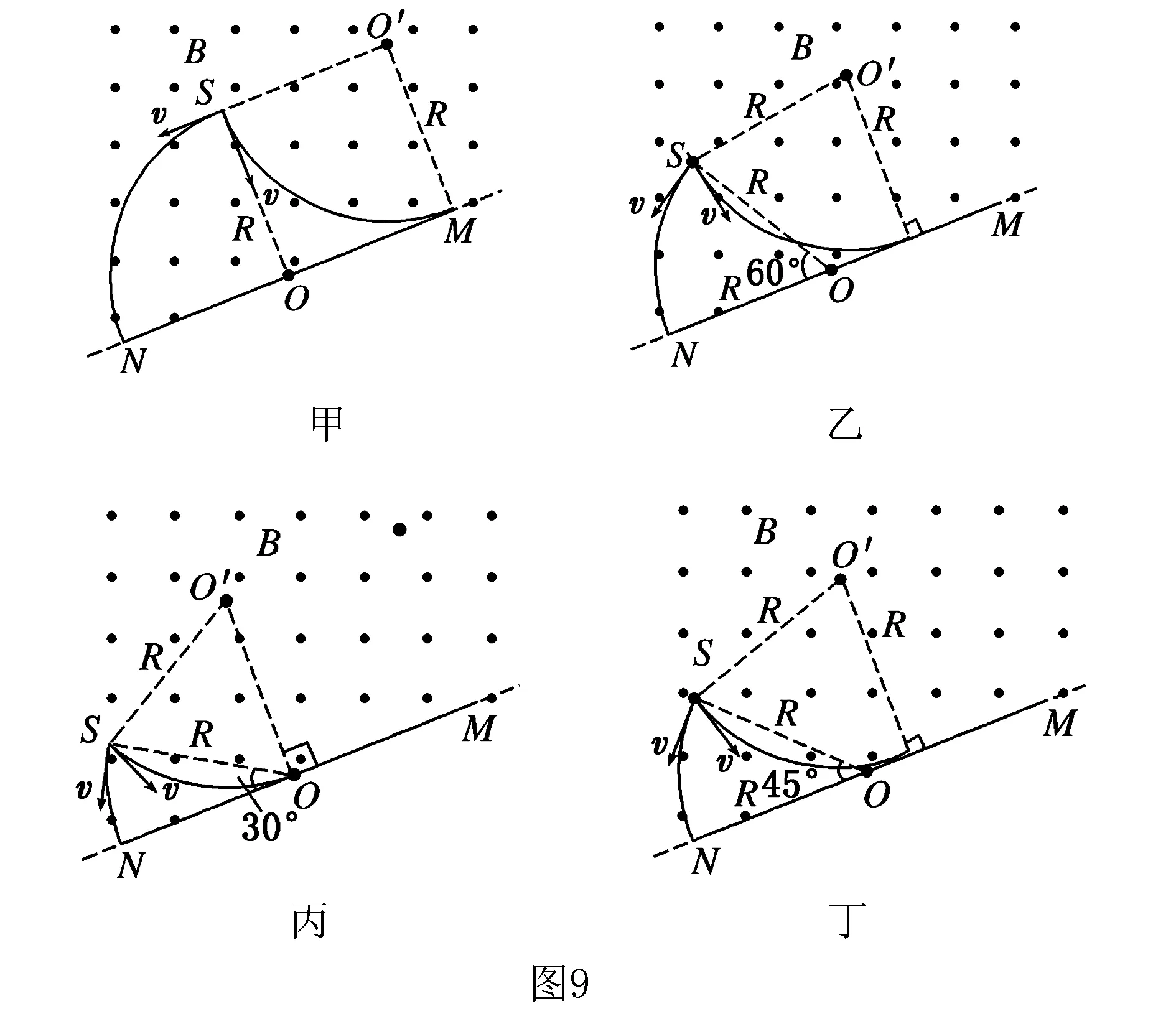
点评本题中，匀强磁场的磁感应强度恒定，一束粒子的电荷量，质量相同，速度方向相同，速率大小不同，他们的轨迹组成一组半径逐渐增大的缩放圆.方法一当半径r≤0.5R和r≥1.5R时，粒子分别从ac、bd区域射出，磁场中的轨迹为半圆，运动时间等于半个周期.当0.5R

三、带电粒子穿出磁场时打在在磁场边界区域范围

当带电粒子通过有界磁场区域时，如果带电粒子的初始速度不同或者磁感应强度大小不定，则各粒子在磁场中运动的轨迹不同，由于边界(或极板/荧光屏)的约束，一部分粒子打在边界(或极板/荧光屏)上，从而产生粒子穿出磁场时打在在磁场边界区域范围的求解问题.此类问题一般需要推理出带电粒子穿出磁场时打在在磁场边界上距离最远的极值条件(轨迹与边界相切或打在边界时轨迹对应的弦长最长)，画出极值条件下的的运动轨迹图， 应用“极值轨迹+几何关系”，结合物理规律求解．也可选取一般情形，画出轨迹图，结合几何关系，列出相关物理量之间的函数关系，通过数学方法求极值.

例题3 (多选)(2015·四川高考)如图7所示，S处有一电子源，可向纸面内任意方向发射电子，平板MN垂直于纸面，在纸面内的长度L=9.1 cm，中点O与S间的距离d=4.55 cm，MN与SO直线的夹角为θ，板所在平面有电子源的一侧区域有方向垂直于纸面向外的匀强磁场，磁感应强度B=2.0×10-4T，电子质量m=9.1×10-31kg，电量e=-1.6×10-19C，不计电子重力，电子源发射速度v=1.6×106m/s的一个电子，该电子打在板上可能位置的区域的长度为l，则( ).

A．θ=90°时，l=9.1 cm B．θ=60°时，l=9.1 cm

C．θ=45°时，l=4.55 cm D．θ=30°时，l=4.55 cm

答案：AD

方法一：分别画出四种对应情况下的极值轨迹图，结合几何关系求解极值条件.θ=90°时，击中板的范围如图9甲，电子轨道正好与MN相切于M点，l=2R=9.1 cm，选项A正确；θ=60°时，击中板的范围如图9乙所示，临界情况电子轨道正好与MN相切，但切点在OM之间，l<2R=9.1 cm，选项B错误；θ=30°，如图9丙所示，显然临界情况电子轨道与MN相切，切点正好与O点重合，l=R=4.55 cm，当θ=45°时，击中板的范围如图9丁所示，显然临界情况电子轨道与MN相切于切点，在OM之间，l>R(R=4.55 cm)，故选项D正确，选项C错误.

点评本题中，应为入射点的位置在发生变化，对应四个选项中，SO与MN的夹角各不相同，方法一要分别分析四种情形下的“极值轨迹+几何关系“，应用方法二只需析一种情形下的极值和几何关系，不过方法二对几何关系的分析和三角函数知识要求较高，具体问题中还需要根据实际情况选择合适的解决方法.

综上所述，带电粒子在有界磁场的临界极值问题，需要挖掘隐含条件、分析临界状态、确定极值条件、明了几何关系、结合数学知识、运用物理规律，对空间想象能力、推理分析能力要求较高.在分析过程中，对应相关的问题模型，可以利用动态的运动轨迹，采用“临界或极值轨迹+几何关系”，探索临界与极值条件，结合物理规律解决问题；也可以采用“一般轨迹+几何关系”，推理相关物理量的函数关系，利用数学知识求解临界极值条件，结合物理规律求解.