基于位姿状态的林区道路视觉导航

颜松，姚立健*，曾松伟，王露露，柴善鹏

(1.浙江农林大学工程学院，杭州 311300；2.浙江农林大学信息工程学院，杭州 311300)

林产品及营林物资在育林、护林、造林等工作中的运输是林业生产的重要环节之一[1-2]。目前常采用履带车[3]、轮式车[4]、轨道车[5]和架空索道[6]等载运工具，以减轻生产者的劳动强度并提高劳动效率，但是这些载运工具存在线路固化、灵活性低、智能化程度不高等不足。近年来，我国加强了森林抚育基础设施的建设，如在林区修建便于抚育间伐、修枝、施肥等作业的水泥硬化营林道路[7-8]，这为无人驾驶林区运输装备的使用提供了保障。

无人驾驶的关键技术有定位方法和导航控制等。在定位方法研究中，机器视觉[9]能感知导航路径中的道路细节，成为GNSS(global navigation satellite system)等精确林业领域全局导航的有益补充[10-11]，极大提高了导航的可靠性。Yuan等[12]在深度神经网络(deep neural network，DNN)边缘分割基础上，提出了基于相关性逐层传播(layer-wise relevance propagation，LRP)的空间注意力(spatial attention)框架，该方法将2个深度模型以当前道路分割数据集，实现更好的泛化性能。武历颖等[13]研究了一种快速准确的非结构化道路检测方法，该方法在基于模糊集的基础上结合了图像灰度特征和道路模型。段志刚等[14]提出了一种光照不变图像的阴影图像道路分割方法，依据阴影区域与非阴影区域的线性关系，选取正交分解法获取彩色光照不变图像，并通过构造的投票函数及道路判别准则提取道路区域。还有学者将卷积神经网络[15]、模糊粗糙集[16]等算法应用于非结构化道路分割中，以提高图像的分割质量。目前，非结构化道路分割主要是提取道路的边缘、颜色、纹理、阴影等特征，将道路区域进行分割。这类方法只考虑当前像素点的灰度分布，像素之间互相独立，分割质量受噪声影响较大。李云伍等[17]研制出适合丘陵山区自主行驶的转运车及其视觉导航控制，主要采用农机运动学模型的路径跟踪控制方法，该方法选取合适导航跟踪点，获得转运车的位姿状态。李天华等[18]提出了适合大拱棚运输车的视觉导航方法，该方法使用道路尽头横向中心点作为导航信息的标定点，进而计算出运输车的位姿信息。上述视觉导航的位姿获取主要集中在道路尽头处理和导航跟踪点选取，但是未考虑在道路左右边缘不完整下的位姿状态获取，研究成果也主要应用于田间道路自主导航，对于林区道路的自主导航研究较少。

笔者以林区中的营林道路为研究对象，搭建适合该环境的试验平台及其视觉导航控制系统。在分析林区道路与背景色差的基础上，采用二维最大类间方差法实现图像分割，从而获得车辆虚拟的导航线，进而求出车体相对于导航线的横向偏差和航向偏差，最后采用纯追踪导航方法验证了本研究算法的有效性。本方法可为林区自动导航运输车的研究提供新思路。

1 材料与方法

1.1 试验材料与控制系统

试验平台以锂电池(48 V、20 Ah)供电，采用前轮转向后轮驱动的四轮结构，主要由电动推杆(BXTL150)、电机驱动器(AQMD6020BLS)、主控制器(STM32F767IGT6)、机器视觉模块(OpenMV)和GPS接收模块(Trimble BD982)等组成，如图1所示。试验平台的位置和姿态信息由机器视觉模块提供，视觉模块摄像头(OV7725)输出图像分辨率为320 pixel×240 pixel，导航时摄像头离地高度和俯角分别为1 m和30°。GPS记录平台的轨迹(point_x，point_y)。机器视觉模块对林区道路图像处理后生成导航线，进而求出试验平台相对于导航线的横向偏差(d)和航向偏差(θ)，并将位姿偏差信号输入主控制器。主控制器根据误差校正模型对位姿偏差信息进行校正，通过纯追踪算法计算出前轮所需转角(α)，根据前轮转向模型将α折算成电动推杆所需的PWM(pulse width modulation)信号，并通过驱动器输出控制电压Uf实现前轮转向。主控制器还控制后轮驱动器输出合适的控制电压Ur使车速(v)达到试验要求。前后轮均设有编码器以检测前轮实际转角和后轮实际转速，以实现对试验平台运动状态的精准闭环控制。试验平台控制系统如图2所示。

1. 电动推杆；2. 电源；3. 摄像头；4. GPS天线；5. 差速器；6. 直流电机；7. 控制器；8. 后轮电机驱动器。图1 试验平台与试验环境Fig. 1 Test platform and test environment

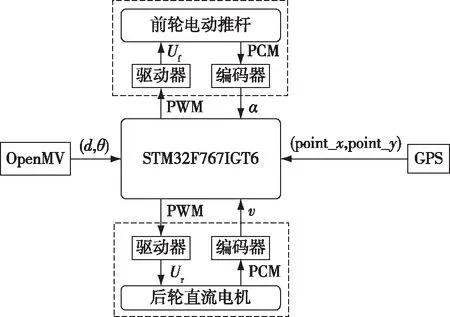
图2 试验平台控制系统Fig. 2 Control system of test platform

1.2 林区道路图像分割

1.2.1 色差统计

从复杂的林区背景中准确识别出林区道路区域是实现视觉导航的前提。手工分割道路图像如图3所示，为更好地发现目标和背景的差异，将图3a中的目标和背景手工分离，如图3b和c所示。

图3 手工分割道路图像Fig. 3 Manually segment road image

对图3b和c中各R、G和B分量进行代数运算以选择合适的分割通道。因林区背景多为绿色，所以选用R、B、R-G、B-G、R+B-G、2R-G、2B-G等7个组合作为备选通道，分别对其目标和背景进行直方图统计，如表1所示。

表1 目标和背景灰度范围Table 1 Target and background gray scale range

由表1可知，B、R+B-G、2R-G和2B-G这4个通道的灰度范围差异明显，因此，选取这4个通道作为图像分割备选通道，再采用合适的分割方法优选出最佳通道。

1.2.2 二维Otsu阈值分割

Otsu法又称最大类间方差法[19]，是通过分析图像灰度直方图获得最佳阈值，将图像分割成方差最大的两类。为充分利用图像邻域像素的灰度分布和像素灰度级的数列分布信息，本研究采用二维Otsu阈值分割法，算法流程如下。

设图像I1灰度等级为L，计算I1中每个像素点3×3邻域的灰度平均值，生成邻域均值图像I2，I1和I2具有相同的分辨率和灰度等级。将I1和I2同一位置的灰度值分别存放于向量i和j中，形成二元组(i,j)。分别以图像I1和I2的灰度等级为横、纵坐标LI1和LI2，以此构建二维直方图，如图4所示。直方图中任意一点的值(pij)定义为：

pij=fij/(W×H),i、j∈[0,L-1]

(1)

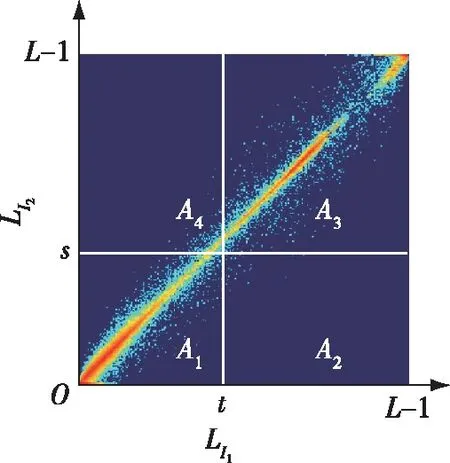
图4 二维直方图的平面坐标投影Fig. 4 Plane coordinate projection of two-dimensional histogram

任意给定一个阈值分割点(s,t)，将图4分为A1～A4等4个部分，目标(A1)和背景(A3)出现的概率w0(s,t)和w1(s,t)分别为：

(2)

式中，Pr(·)表示对应部分发生的概率。由图4可得，w0+w1≈1，可计算目标和背景的均值矢量μ0和μ1，则图像总均值矢量μT=w0μ0+w1μ1，定义目标和背景的类间离散测度矩阵[20]为：

(3)

离散测度矩阵的秩为：

tr[Sb(s，t)]=[(w0μTi-μ0i)2+

(w1μTj-μ0j)2]/(w0w1)

(4)

则图像的最优分割阈值为tr[Sb(s,t)]取得最大值时的解集(s′,t′)。

采用上述方法分别对图3a各通道图像进行分割，并采用5×5均值滤波器进行去噪处理，得到的分割效果如图5所示。

由图5可知，4个通道分割后的图像均能很好地显示道路轮廓。以下将提出一种定量方法来评价图像分割质量，以便选出最优的色差通道。

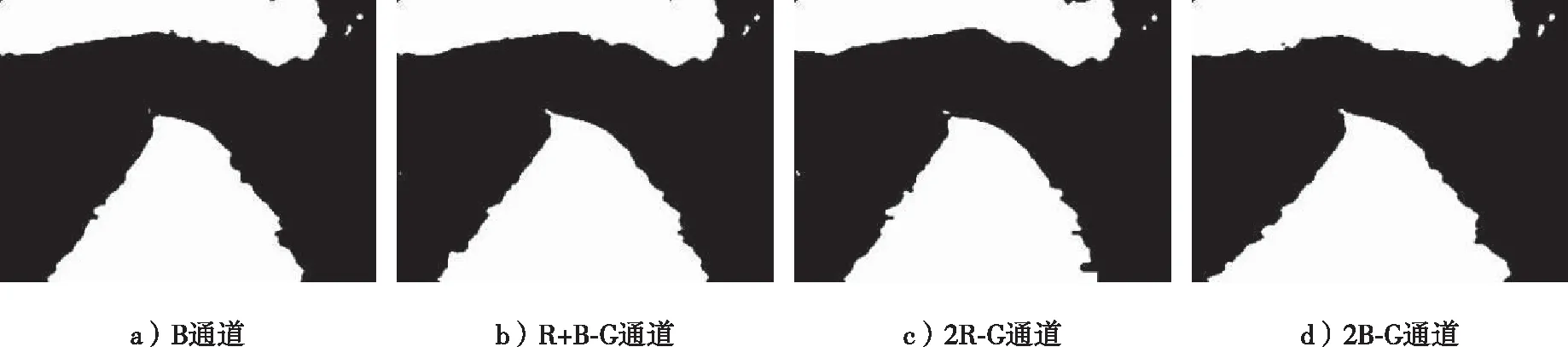
图5 不同色差通道下的分割效果Fig. 5 Segmentation effects under different color-difference channels

1.2.3 图像分割质量定量评价

设P为采用手工方法分割后的道路二值图像，该图像为标准参照图像；Q为采用二维Otsu法分割后得到的道路二值图像。为检验Q图像分割的质量，定义真阳率(TPR，式中表示为TPR)为Q中相对于参照图像P分割正确部分的占比，定义假阳率(FPR，式中表示为FPR)为Q中相对于P分割错误部分的占比，则：

(5)

式中：num(P)为P图中目标的像素数；num(P∩Q)为Q图相对于P图分割正确的目标像素数；num(Q-P∩Q)为Q图相对于P图分割错误的像素数。由式5可知，TPR越大且FPR越小，则图像分割的质量越高。通过计算，图5中4幅不同色差通道的TPR和FPR依次分别为88.9%，92.1%，89.2%，95.1%和11.6%，8.6%，11.3%，8.2%。由此可知，2B-G通道下的分割质量最好，因此本研究选取基于2B-G通道的二维Otsu法。

1.3 平台位姿状态获取与校正

1.3.1 位姿状态获取

在机器视觉导航中，车体位姿状态的估算是关键步骤之一，该位姿状态主要表现为摄像头实时采集到的横向偏差和航向偏差。在位姿估算中，首先需要对图像信息进行充分挖掘后提取正确的道路区域，选取动态导航图像中道路左右侧背景区域在图像左右边缘上的投影长度为检测道路边缘状态的评判标准。根据样本可得道路图像主要分为如图6所示的4种情况，其边缘分析如表2所示。

图6 模拟导航道路图像Fig. 6 Simulated navigation road images

表2 道路图像边缘分析Table 2 Edge analysis of road images

图6d中道路左右边缘均未完整显示，这是视觉导航中最常见的一种状态。因此，以图6d为例，建立位姿状态获取示意图(图7)，C1为图像底端中心点，由于相机置于试验平台纵轴中心线最前端处，因此C1点为试验平台当前位置， 通过C1点竖直向上的向量C1C2即为试验平台当前航向。当Hl

图7 车辆位姿状态示意图Fig. 7 Schematic diagram of vehicle pose state

在实际计算时，d像素值转换是以图像底端的实际距离为基准，进行像素与实际距离比例转换成米制距离。图7中直线C3C4的方程表达式关系到d和θ的准确性，为保证该方程获取的可靠性，将第Hl行以上区域横向划分为多个区域并求各区域的中心点，结果如图8所示。以相邻点之间的斜率均值为直线C3C4的最终斜率(k)，求第Hl行以上道路区域中心点C0为直线C3C4的通过点。

图8 林区道路区域位姿状态示意图Fig. 8 Schematic diagram of the pose state of the forest road area

1.3.2 位姿状态校正模型

由于存在相机内参、镜头畸变、仿射变换等因素，推算出来的位姿与实际值必然存在误差，因此建立一个误差校正模型对位姿进一步校正。将试验平台以不同位姿置于林区道路上，以实际的横向偏差和航向偏差为横、纵坐标轴，以上述位姿状态获取模型推算值与实际值之间的偏差Δd和Δθ值为坐标值，分别构建θ-d-Δd和θ-d-Δθ2个位姿误差高程图(图9)。根据试验道路宽度及相机视角确定d和θ的范围分别为(-25 cm,25 cm)和(-20°, 20°)。

图9 位姿误差高程图Fig. 9 Pose error elevation map

采用Matlab R2014a对散点图进行曲面拟合，得二元多项式方程(式6)，各项系数如表3所示。

Δd,θ(d,θ)=a3d3+a2d2+a1d+b3θ3+b2θ2+b1θ+c3d2θ+c2dθ2+c1dθ+c0

(6)

式中，(d,θ)为误差位姿的测量值。

表3 多项式方程系数Table 3 Polynomial equation coefficients

本研究中2个拟合方程的决定系数分别为0.897 3 和0.882 9，拟合效果较好，则位姿推算值修正方程为：

(7)

式中，dcorrection和θcorrection分别为测量位姿修正后的横、纵坐标。

为验证偏差位姿方法的有效性，本研究将随机选取该范围中16个不同车体位姿的测量值，统计得θ方向和d方向相对于实际值的平均误差分别为4.3°和10.8 cm。将测量值代入式7中，得到θ方向和d方向修正后的平均误差为1.7°和1.6 cm，位姿精度分别提升了60.5%和85.2%。将修正后的位姿代入纯追踪控制模型中，以d、θ和前视距离为输入量，前轮转向角为输出量实现导航控制，其中，前视距离是决定转向角的关键因素[21]。考虑相机视角的限制和路面凹凸不平、宽度等因素，选取图7中的F点为最近预瞄点，C4为最远预瞄点，并通过Matlab R2014a多次仿真，选取最优前视距离为3.5 m，该前视距离为预瞄点到试验平台后轴中心的距离。

2 结果与分析

2.1 试验过程

为验证本研究算法的有效性，在浙江农林大学林学实验基地对试验平台进行视觉导航试验。该基地为科研竹林，营林道路以2.1～3.1 m宽度的直线路段为主。摄像头位于试验平台纵轴中心线最前端位置，且离地面高度1 m，俯角为30°，采样帧率为5帧/s，试验平台前进速度为0.5 m/s，试验环境如图1所示。

设置3种不同的初始状态，在机器视觉系统引导下完全自主行驶。采用平均偏差、标准差、稳态偏差、调整时间等指标分析导航试验效果。行驶距离是试验平台由起点行驶到终点的水平距离；偏差是试验平台的横向偏差和航向偏差的总称；稳定状态是试验平台收敛至横向偏差为±2 cm且航向偏差为±2°时的状态；调整时间是图7中试验平台从C1C2调整到稳定状态所需的时间；平均偏差是试验整个过程偏差的均值；标准差是各个偏差偏离平均偏差距离的均值；稳态偏差是试验平台收敛至稳定状态后偏差的均值；稳定距离是试验平台第1次到达稳定状态时的水平距离；最大偏差是试验整个过程偏差极值中的最大值。试验效果及试验数据如图10、表4和5所示。

图10 不同初始状态下试验平台的导航效果Fig. 10 The navigation effects of the test platform in different initial states

表4 不同初始状态下的偏差信息Table 4 Deviation information in different initial states

表5 不同初始状态下的控制指令与效率Table 5 Control commands and efficiency in different initial states

2.2 结果分析

1)在3种初始状态下，试验平台的平均横向偏差分别为5.8，5.9和4.6 cm，最大横向偏差分别为20.6，23.9和25.3 cm，试验平台平均航向偏差分别3.5°，3.5°和4.0°，最大航向偏差分别为13.7°，16.1°和25.0°。这说明最大偏差与初始状态有关，不同初始状态下平均横向偏差均值为5.4 cm，平均航向偏差均值为3.7°。当试验平台行驶到稳定状态后，稳态横向偏差分别为2.7，2.3和1.6 cm，均值为2.2 cm；稳态航向偏差分别为1.9°，2.4°和2.1°，均值为2.1°。根据上述分析可得，试验平台沿林区期望导航线自主行驶的平均相对误差均值为5.2%，当到达稳定状态后，其稳态偏差均能保持在2 cm和2°左右，满足林区导航精度的要求。

2)在数据统计中，标准差可反映数据的离散程度。因此，试验平台平均偏差和稳态偏差的标准差可反映自主行驶的稳定性。在3种初始状态下横向偏差的平均标准差分别为5.8，6.9和5.5 cm，航向偏差的平均标准差为3.1°，3.4°和5.1°，而稳态横向偏差的标准差分别为2.2，1.6和1.8 cm，稳态航向偏差的标准差为1.7°，2.1°和2.1°。由上述数据可得，试验平台的平均标准差均值分别为6.1 cm和3.8°，而稳态标准差均值为1.8 cm和2.0°，稳态标准差均在2 cm和2°左右，具有较低的离散程度，说明试验平台在各初始状态下行驶的稳定性较好。

3)收敛性能是检测系统好坏的重要参数之一。在图7中，试验平台从C1C2到稳定状态所需的调整时间可反映试验平台的收敛性能，此时的稳定状态与C3C4有关。3种初始状态下的调整时间分别为15.2，10.5和14.4 s，其对应的稳定距离分别为5.6，4.0和4.5 m，图10b中初始偏差相对较小，相对应的调整时间也较小，收敛速度也较快。图10a和c中初始偏差较大，调整时间相对于图10b分别增加了49.5%和41.9%。综上所述，试验平台具有较好的收敛性能。

4)在实际的林区环境中，由于路面会出现凹凸不平等情况，所以控制系统输出的期望转角不宜过大，以防止车体的侧翻。由表5可得，各初始状态下期望转角的总范围为-9.7°～7.9°，全程期望转角应控制在-10°～10°，从而提高车体的抗侧翻性能。

3 结 论

根据林区道路的特点，选用基于2B-G通道的二维Otsu图像分割方法。对动态道路图像的边缘状态进行分析，建立基于边缘不完整的位姿状态获取示意图，并随机选取位姿状态校正模型内16个不同车体位姿，误差修正后位姿与实际位姿平均误差分别为1.7°和1.6 cm。通过试验表明，自主行驶轨迹的横向和航向平均偏差分别为4.6～5.9 cm和3.5°～4.0°，稳态偏差均值为2.2 cm和2.1°，可满足林区自主导航作业的要求。后续将考虑树枝遮挡物、道路破损、崎岖不平等林区真实环境对自主行驶轨迹的影响，同时引入最优路径规划和避障等算法，进一步改善自主导航的质量。